Journal of Food Processing and Preservation

Volume 46, Issue 12 e17179

ORIGINAL ARTICLE

Open Access

Water sorption isotherms of different sodium alginates: Thermodynamic evaluation and influence of mannuronate-guluronate copolymers

Leticia Montes,

Leticia Montes

orcid.org/0000-0001-9758-4142

Chemical Engineering Department, Universidade de Santiago de Compostela, Santiago de Compostela, Spain

Search for more papers by this author

Mauro Gisbert,

Mauro Gisbert

orcid.org/0000-0001-5923-4651

Chemical Engineering Department, Universidade de Santiago de Compostela, Santiago de Compostela, Spain

Search for more papers by this author

Ramón Moreira,

Corresponding Author

Ramón Moreira

[email protected]

orcid.org/0000-0002-6388-0063

Chemical Engineering Department, Universidade de Santiago de Compostela, Santiago de Compostela, Spain

Correspondence

Ramón Moreira, Department of Chemical Engineering, Universidade de Santiago de Compostela, rúa Lope Gómez de Marzoa, Santiago de Compostela E-15782, Spain.

Email: [email protected]

Search for more papers by this author

Leticia Montes,

Leticia Montes

orcid.org/0000-0001-9758-4142

Chemical Engineering Department, Universidade de Santiago de Compostela, Santiago de Compostela, Spain

Search for more papers by this author

Mauro Gisbert,

Mauro Gisbert

orcid.org/0000-0001-5923-4651

Chemical Engineering Department, Universidade de Santiago de Compostela, Santiago de Compostela, Spain

Search for more papers by this author

Ramón Moreira,

Corresponding Author

Ramón Moreira

[email protected]

orcid.org/0000-0002-6388-0063

Chemical Engineering Department, Universidade de Santiago de Compostela, Santiago de Compostela, Spain

Correspondence

Ramón Moreira, Department of Chemical Engineering, Universidade de Santiago de Compostela, rúa Lope Gómez de Marzoa, Santiago de Compostela E-15782, Spain.

Email: [email protected]

Search for more papers by this author

First published: 23 September 2022

https://doi.org/10.1111/jfpp.17179

Citations: 6

Share a link

Email
Wechat
Bluesky

Abstract

Water desorption isotherms of three alginates with different structural features were determined at 25, 37, and 50°C. The Halsey model was selected to fit the equilibrium water sorption data. Differential and integral enthalpy and entropy were estimated for tested alginates. Optimal storage conditions of tested alginates (moisture content from 0.15 to 0.20 kg water/kg dry solid and relative humidity from 35% to 50%) were determined from the maximum and minimum integral enthalpy and entropy values, respectively. A model was proposed to estimate the water sorption isotherms of alginates based on the alginate monomers (mannuronate, M, and guluronate, G) at low water activity (<0.4). M fraction was mainly responsible for the hygroscopicity of alginates. Alginates with similar G fraction showed different hygroscopic features by the presence of more homopolymeric G blocks that could form helical structures at low moisture content, decreasing the water affinity.

Practical applications

Determination of water sorption isotherms is fundamental to determine the optimal storage conditions at different temperatures. Their knowledge is essential for designing drying equipment, selecting adequately drying conditions (temperature and relative humidity of air) and drying time. Mathematical models are useful to estimate equilibrium moisture content in wide ranges of water activity and temperature. The thermodynamic study also provides valuable information about energy consumption and consequently operational costs. In this case, high content of mannuronate, M, increases the hygroscopic character of alginates, but the optimal moisture content of dried alginates to achieve maximum stability during storing varies in a narrow interval (0.15–0.20 kg water/kg dry solid).

1 INTRODUCTION

Alginate extraction from brown seaweeds is based on the conversion of the alginic acid from the cell walls into alginate salt forms, followed by its precipitation and purification. Milled seaweeds are soaked in dilute mineral acid to remove fucoidans, laminarins, proteins, and polyphenols that could modify alginate features. Then, alginic acid is transformed into sodium alginate (SA) by employing alkaline solutions, meanwhile solid residues are removed by centrifugation and filtration. Finally, alginate is precipitated with ethanol to obtain SA (Chee et al., 2011). Recent studies have showed that SA can also be obtained from wasted solids after polyphenols extraction (Montes et al., 2021). SA is a linear polysaccharide composed of β-D-mannuronic acid (M) and α-L-guluronic acid (G) linked by 1–4 glycosidic bonds, and the M/G ratio gives relevant information about the polymer structure (Abka-khajouei et al., 2022). The composition of alginates depends on their natural source, geographical location, and seasonal variations (Fernando et al., 2020). SA is used in cosmetic, pharmaceutical, medical, and textile industries. Particularly, it is widely used in food industry due to its thickening, emulsifying, gelling, stabilizing, and film-forming properties, being one of the most important food additives (Qin et al., 2018).

SA is a hygroscopic material and tends to modify its moisture content as a function of environmental air conditions; hence, adequate storage conditions are very relevant for its correct conservation (Lee & Mooney, 2012). Most biopolymers are sensitive to moisture content, so their properties change with relative humidity and temperature (Kurek et al., 2014). By means of water sorption isotherms, which relate the equilibrium moisture content (X) and water activity (a_w), the optimally hygroscopic conditions can be obtained for its preservation (Shivhare et al., 2004). There are many (empirical, semitheoretical, and theoretical) equations to model the water sorption isotherms. Halsey model can be used to study the multilayer water adsorption (Halsey, 1948). In this model, temperature can be introduced as variable within the model, and one equation is useful to reproduce simultaneously the equilibrium moisture content of a sample over a broad water activity and temperature ranges.

Hygroscopic properties of a food material depend on its chemical composition (Moreira et al., 2009). In this way, the presence of additives such as SA can noticeably modify the equilibrium moisture content of the final product under the same storage conditions. At these circumstances, it is crucial to knowledge the hygroscopic behavior of compounds present in food and non-food formulations. To understand the SA water sorption features and to estimate its optimal storage conditions, some thermodynamic properties can be evaluated such as differential heat of sorption and differential entropy, as well as the integral enthalpy and entropy (Zhang et al., 2016). The differential enthalpy of sorption is an indicator of the water binding strength to the solid, meanwhile the differential entropy is proportional to the number of available sorption site corresponding to a specific energy level (Koksharov et al., 2021). On the other hand, the integral enthalpy provides an indication of the total energy available to do work, and the integral entropy describes the degree of disorder and randomness of motion of water molecules (Moreira et al., 2008).

There are some studies concerning the water sorption isotherms of alginates. For instance, Galus and Lenart (2013) studied the water adsorption isotherms of SA at 25°C, and the experimental data were successfully fitted by Peleg's model. Adamczak et al. (2017) determined water adsorption and desorption isotherms of SA at 25°C, with slightly higher moisture content for desorption in comparison to adsorption process. Xiao and Tong (2013) employed GAB model to fit experimental data of water adsorption of low-viscosity SA in the temperature range from 25 to 45°C.

Previous results indicate discrepancies in the literature regarding hygroscopic properties of SA due to probably the different sources and extraction procedures employed to obtain commercial SA. To the best of our knowledge, no studies relating the sorption isotherms features with the structural features of alginates were found. Therefore, the goals of this study were to: 1. determine water sorption characteristics of SA with different M/G ratios and their modeling using the Halsey model; 2. evaluate some thermodynamic properties to understand sorption phenomena in depth and to assess the optimal storage conditions for dried SA; and 3. establish the relationship between M/G ratio of the different SA and the corresponding water sorption isotherms.

2 MATERIALS AND METHODS

2.1 Materials

Processed and commercial sodium alginates (SA) were used. Specifically, processed SA from Ascophyllum nodosum brown seaweeds was obtained using a previously reported methodology (Montes et al., 2021), seaweeds pellets dried at 50°C (50D). Commercial sodium alginates (CAS No. 9005-38-3) were purchased from Sigma-Aldrich Chemical Company (S) (Lot MKCJ1280, St. Louis, MO, USA) and PanReac (P) (Lot 0F009964, Barcelona, Spain). Average viscosimetric molecular weights (M_v, kg/mol), P (459 ± 8), S (156 ± 2), and 50D (257 ± 1) and the corresponding average block length, mannuronate-guluronate ratio (M/G), P (1.15), S (0.91) and 50D (1.21), diads (F_GG), P(0.23), S (0.35) and 50D (0.20) and triads (F_GGG) P(0.13), S (0.30) and 50D (0.10), were previously determined by Montes et al. (2021).

2.2 Determination of water desorption isotherms

A gravimetric technique was carried out to determine the equilibrium moisture content of SA samples. Firstly, samples were hydrated for 3 weeks until constant weight. Then, several jars were prepared with different saturated salt solutions to obtain atmospheres with constant water activity. The salt solutions used were LiCl, MgCl₂, Mg(NO₃)₂, NaCl, KCl, and BaCl₂, which were prepared according to Moreira et al. (2008). The range of relative humidity of air achieved with these salts was within the interval 11%–90%. The samples (0.5 g), previously weighted, were placed in glass jars and introduced in the flasks at three temperatures: 20, 37, and 50°C (±0.1°C). Thymol was introduced in the jars to inhibit microbial growth at relative humidity higher than 0.6.

An analytical balance (SI-234, Denver Instrument, ±0.0005 g) was used to weight the samples at regular intervals until constant weight. The time required to achieve the equilibrium was about 12 weeks. The moisture content was determined using a vacuum oven (Vacutherm VT650, Heraeus Hanau) at 70°C and 13 kPa until achieve constant weight. The equilibrium moisture content (X) was measured for all samples, and the water sorption isotherms curves were plotted as X versus a_w. All experiments were done at least in duplicate.

2.3 Data analysis

2.3.1 Sorption isotherms models

The experimental results were fitted by Halsey model, Equation (1):

X = {(\frac{- A}{T \ln (a_{w})})}^{\frac{1}{r}}

(1)

where X is the equilibrium moisture content (kg water/kg dry solid, d.b.), a_w is the water activity, T (K) is the absolute temperature, and A and r are the fitting parameters of Halsey model.

2.3.2 Differential and integral enthalpy and entropy

The complete and detailed procedure is explained in Moreira et al. (2008). Briefly, the isosteric heat of sorption, Q_st (kJ/mol), (or differential enthalpy) is an indicator of the state of water absorbed by the solid material and is defined by Equation (2):

Q_{st} = q_{st} + H_{L}

(2)

where q_st (kJ/mol) is the net isosteric heat of sorption, and H_L (kJ/mol) is the heat of vaporization of water at the sorption temperature. Using the Clausius–Clapeyron relationship, q_st at constant X can be evaluated from the experimental data by Equation (3):

q_{st} = - R {[\frac{d \ln a_{w}}{d (1 / T)}]}_{X}

(3)

where R (kJ/mol K) is the universal constant of gases.

The differential entropy, S_d (kJ/mol K), of water adsorption can be calculated from Gibbs–Helmholtz equation and substituting the Gibbs energy by its definition, a linear equation, Equation (4), involving Q_st, S_d, and a_w, is obtained:

\ln {(a_{w})|}_{X} = \frac{Q_{st}}{RT} - \frac{S_{d}}{R}

(4)

where the S_d value can be calculated from the intercept (S_d/R).

The net integral enthalpy, q_eq (kJ/mol), must be evaluated at constant spreading pressure,

\emptyset

(J/m²), according to Equation (5):

q_{eq} = - R {[\frac{d \ln (a_{w})}{d (1 / T)}]}_{\emptyset}

(5)

The spreading pressure represents the surface excess free energy and provides an indication of the increase in surface tension of bare sorption sites due to adsorbed molecules (Fasina et al., 1999). This property cannot be experimentally measured but can be estimated by Equation (6).

\emptyset = \frac{K_{B} T}{A_{m}} a^{1 / r} {[\frac{1}{(\frac{1}{r} - 1) {(- \ln (a_{w}))}^{\frac{1}{r} - 1}}]}_{0.05}^{a_{w}}

(6)

where K_B is the Boltzmann's constant (1.38 × 10⁻²³ J/K), A_m represents the area of a water molecule (1.06 × 10⁻¹⁹ m²), a is A/T.

Finally, the net integral entropy, S_eq (kJ/mol K), is calculated by Equation (7):

S_{eq} = \frac{- q_{eq}}{T} - R \ln (a_{w})

(7)

where a_w is obtained at constant

\emptyset

at different T.

2.4 Statistical analysis

Experimental data were analyzed through one-factor analysis of variance (ANOVA), followed by the Duncan test, and considering significant p values <0.05 (IBM SPSS Statistics 27, SPSS Inc). All experimental results were expressed as mean ± standard deviation from at least duplicate experiments.

The goodness of fitting of Halsey model was estimated by two statistical indices previously proposed by Moreira et al. (2017), φ (Equation [8]), which is a lumped measure and involves the coefficient of determination (R²), the root mean squared error (RMSE) and the mean relative deviation (MRD), and χ². If φ shows low values, the model shows a poor adequacy to describe the experimental behavior, and if the value of χ² ≥ 5.99, the model should be rejected with p > 0.95.

φ = \frac{R^{2}}{(RMSE) (MRD)}

(8)

3 RESULTS AND DISCUSSION

3.1 Experimental water desorption isotherms and modeling

Experimental data of equilibrium water desorption isotherms of different sodium alginates (SA) at 20, 37, and 50°C are depicted in Figure 1. Water sorption isotherms can be classified as type III according to BET classification (Brunauer et al., 1940). All tested SA showed the same temperature trend at constant water activity, X decreased with increasing temperature. In all cases, at a constant temperature, the equilibrium moisture content (X) increased with increasing water activity (a_w). However, two different regions in the isotherm curves can be observed. Firstly, a linear trend was observed at low and intermediate a_w values (from 0.1 to 0.5), this region is called multilayer sorption region. Secondly, at higher a_w values, the capillary condensation region can be observed by the pronounced increase of X with increasing a_w. Significant differences were found between tested SA in this last region (a_w > 0.5). Particularly, X value at the highest a_w (0.9) was approximately 0.6 (kg/kg d.b.) for S and P alginates (without significant differences between them) and 0.8 (kg/kg d.b.) for 50D. However, below 0.5 of a_w, no significant differences (p ≤ 0.05) were found between tested SA. These results partly agree with those reported previously by Galus and Lenart (2013) at 25°C, that is, at a_w of 0.5 X was 0.25 (kg/kg d.b.); however, at a_w of 0.9 these authors found higher moisture content value (1.3 kg/kg d.b.) for adsorption process. Also, Adamczak et al. (2017) reported higher X values (up to 1.16 kg/kg d.b. at a_w of 0.9), for the water adsorption stage at 25°C. However, Shimanuki et al. (2020) determined, at the same high a_w value, a moisture content approximately 0.5 kg/kg d.b that agreed with results obtained for S and P alginates tested in the present study. Finally, Xiao and Tong (2013) found for water adsorption of low-viscosity SA at 25°C an equilibrium moisture content of 0.4 kg/kg d.b. at a_w of 0.90.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Water desorption isotherms of different alginates: (a) from sigma (S), (b) from PanReac (P), and (c) processed (50D) at 20, 37, and 50°C. lines correspond to Halsey model (Equation [1]).

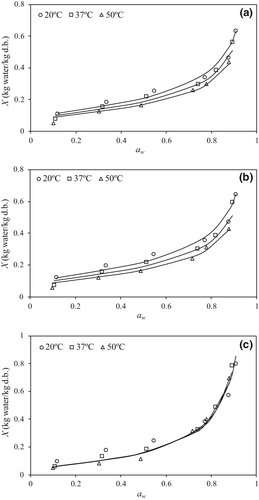
The Halsey model was employed to fit experimental data, desorption isotherms are plotted in Figure 1 by continuous lines, and the corresponding fitting parameters are presented in Table 1. No significant differences (p ≤ 0.05) between Halsey parameters (A and r) for S and P alginates at constant temperature. For these alginates, A values decreased (from 12.08 to 8.73 and from 12.46 to 8.42, respectively) with increasing temperature. However, for 50D, A values increased (from 23.21 to 25.28) with temperature. Interestingly, a (A/T) parameter value was invariant with temperature in the case of 50D alginate. In all cases, the r values were invariant with temperature for each alginate, and 50D showed the lowest value (1.187), meaning the highest slope of the isotherm curve, against S and P alginates (around 1.820).

TABLE 1. Values of the parameters of Halsey model (Equation 1) and goodness of fitting for water sorption isotherms of commercial S (sigma) and P (PanReac) and processed (50D) alginates

Sample	S			P			50D
T (K)	293.1	310.1	323.1	293.1	310.1	323.1	293.1	310.1	323.1
A	12.08 ± 0.84^a,B	10.18 ± 0.77^ab,B	8.73 ± 0.71^b,B	12.46 ± 1.03^a,B	10.17 ± 0.96^ab,B	8.42 ± 0.91^b,B	23.21 ± 1.02^a,A	24.38 ± 1.48^ab,A	25.28 ± 0.84^b,A
a = A/T	0.041 ± 0.003^a,B	0.033 ± 0.003^b,B	0.027 ± 0.002^b,B	0.043 ± 0.004^a,B	0.033 ± 0.003^ab,B	0.026 ± 0.003^b,B	0.079 ± 0.002^a,A	0.079 ± 0.004^a,A	0.078 ± 0.005^a,A
r	1.815 ± 0.076^A				1.847 ± 0.027^A			1.187 ± 0.012^B
φ *	347.5	308.1	1287.5	293.8	183.6	261.3	65.7	319.8	152.8
χ ² **	4.2	3.3	5.4	3.9	5.6	1.1	1.0	0.6	0.1

Note: Data are presented as mean ± standard deviation. Data value of each parameter with different superscript lowercase letters are significantly different by temperature and capital letters by alginate at constant temperature (p < 0.05).
* Low values of φ indicate a poor adequacy of the model.
** With value χ² ≥ 5.99, the model should be rejected (p > 0.95).

3.2 Thermodynamic properties

3.2.1 Differential enthalpy and entropy

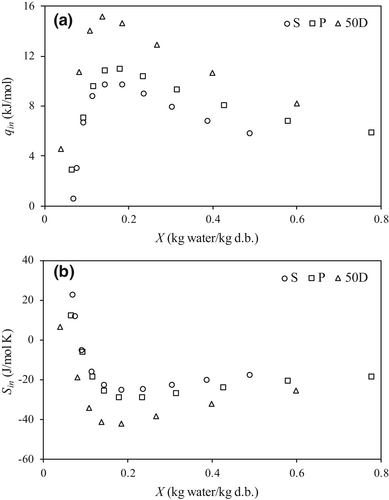
Figure 2a shows the variation of the differential enthalpy (q_st), evaluated by means of Equation (3), with the moisture content of tested alginates at arithmetic mean temperature (35.7°C). At low moisture content, there are high attractive intermolecular forces between alginate surface and adsorbed water. Afterward, a sharp fall in the q_st values is observed when moisture content increases from 0.08 to 0.2 kg/kg d.b., because water molecules are adsorbed in other available sites with lower specific energy (Polachini et al., 2016). Subsequently q_st values dramatically decreased and at moisture content above 0.3 kg/kg d.b., water molecules multilayers were formed and progressively approached zero meaning that the adsorption of a water molecule involved an energy equivalent to the heat of vaporization of Xiao and Tong (2013) employing low-viscosity SA observed this effect, but the values obtained (10 kJ/mol at X of 0.1 kg/kg d.b.) were lower than the values of this work (60 kJ/mol at X of 0.1 kg/kg d.b.). The highest q_st values found at low X (<0.25 kg/kg d.b.) were for P alginate.

Figure 2b shows the trend of differential entropy (S_d), Equation (4), with moisture content of tested alginates at 35°C. S_d is proportional to the number of available sorption sites at a specific energy level. Negative values are related to the loss of mobility of water molecules during sorption. The S_d values increased continuously at low moisture content (below 0.20 kg/kg d.b.) and above this content remained practically constant. At low moisture content, water molecules were strongly retained (high activation energies) in many available sorption sites, but these sites were progressively occupied with increasing moisture content (Madamba et al., 1996).

The theory of compensation needs to be applicable that isokinetic (T_I) and harmonic mean (T_h) temperatures are different and, in the range of moisture content studied, the existence of a linear relationship between differential enthalpy and differential entropy (Moreira et al., 2008). The linear relationship was verified by the plotting of q_st versus S_d and from the slope T_I values were obtained (340, 337 and 329 K for S, P and 50D, respectively), and T_h was 308 K. As T_I > T_h in all cases, the water sorption of tested alginates can be characterized as enthalpy-driven (Moreira et al., 2016).

3.2.2 Integral enthalpy and entropy

Figure 3 shows the spreading pressure, calculated by means of Equation (6), as a function of a_w for tested alginates at studied temperatures. The spreading pressure increased (up to 1.50 J/m²) with increasing a_w and decreased with increasing temperature in all cases. Slight differences were found between spreading pressure values of S and P alginates at constant temperature, and values of 50D alginate were systematically lower. In fact, the $\emptyset$ values for S and P at 50°C were similar to 50D values at 37°C. These trends agreed with results reported for alginates by Xiao and Tong (2013), but with lower values (<0.1 J/m²).

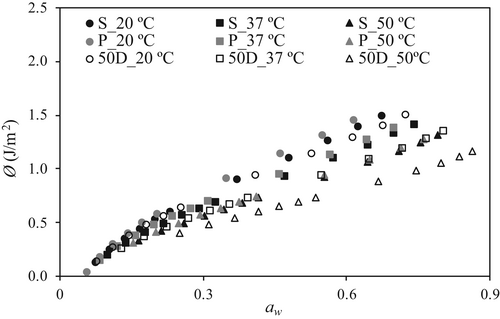
Figure 4a shows the variation of the net integral enthalpy, q_eq, calculated with Equation (5) at constant spreading pressure, with the moisture content. At low X, q_eq increased up to achieve maximum values (9.8, 11.0 and 15.2 kJ/mol for S, P, and 50D, respectively) and then continuously decreased with increasing X. On the other hand, the net integral entropy, S_eq evaluated with Equation (7), decreased at low X reaching a minimum value (−24.9, −28.7 and −42.2 J/mol K for S, P and 50D, respectively), Figure 4b. Both enthalpy and entropy trends with moisture content reflect the transition from the water molecules occupation of easily accessible sites to localized binding followed by the formation of multi-layers (Moreira et al., 2008).

Regarding the integral enthalpy and entropy curves, the maximum enthalpy and minimum entropy values occurred at the same narrow moisture content range from 0.15 to 0.2 kg/kg d.b., for tested alginates. The minimum integral entropy determines the water activity at which the food product has the highest stability, and additionally, other authors indicated that maximum enthalpy is achieved with the formation of a monolayer of adsorbed water (Kaya & Kahyaoglu, 2007). In this case, it means that maximum stability (optimal water activity) is achieved in the interval from 0.35 to 0.45 for S and P alginates and from 0.40 to 0.50 for 50D alginate.

3.3 Relationship between equilibrium moisture content and M/G ratio of alginates

To find a relationship between structural features of alginates and water molecules sorption on the sample surface, the water activity range must be restricted to the water activity range in which the water monolayer is formed. In this case, this a_w interval was below 0.4. Parameters of Halsey model (Table 1) were employed to find correlations with M/G ratio of tested alginates. Firstly, a linear regression (R² > 0.9) was established between guluronate, G, fraction (G/[M + G]) values, and the r parameter from Halsey model. Extrapolating this linear regression to guluronate fraction values of zero and one (G = 0 and M = 0), it could be possible to obtain r values corresponding to hypothetical alginate formed exclusively by M (r_M = 2.074) and by G (r_G = 0.560), respectively. The water content of alginate can be assumed as the sum of water adsorbed on guluronate (X_G) and mannuronate (X_M) surface (Equations [9] and [10]).

X_{G} = G {(\frac{- a_{G}}{\ln a_{w}})}^{\frac{1}{r_{G}}}

(9)

X_{M} = (1 - G) {(\frac{- a_{M}}{\ln a_{w}})}^{\frac{1}{r_{M}}}

(10)

where a_G and a_M are the corresponding parameters for G and M of Halsey model.

The a_G and a_M values were obtained by means of a multivariable optimization procedure with the following objective, Equation (11):

\min [\sum_{a_{w} = 0.1}^{a_{w} = 0.4} X - G {(\frac{- a_{G}}{\ln a_{w}})}^{\frac{1}{r_{G}}} - (1 - G) {(\frac{- a_{M}}{\ln a_{w}})}^{\frac{1}{r_{M}}}]

(11)

where X were the moisture content values given by Halsey model. This procedure was applied to each alginate at constant temperature. As chemical characteristics of M and G are independent of the type of alginate, average a_G and a_M values were obtained after individual optimization of each alginate. The a_G and a_M values were 0.30, 0.26, and 0.24 and 0.052, 0.035, and 0.019 at 20, 37, and 50°C, respectively. These values were linearly correlated (R² > 0.99) with temperature. Therefore, an equation useful to estimate the equilibrium moisture content of alginate with its guluronate and mannuronate content at different temperatures is given by Equation (12):

\begin{matrix} X = X_{G} + X_{M} = G {(\frac{- 0.9616 + 0.002246 T}{\ln a_{w}})}^{\frac{1}{0.5604}} \\ + (1 - G) {(\frac{- 0.3772 + 0.001107 T}{\ln a_{w}})}^{\frac{1}{2.0742}} \end{matrix}

(12)

Analyzing Equation (12), it was observed that the X value was mainly due to the contribution of X_M meaning that M was more hygroscopic than G. For instance, in S alginate at 20°C and at a_w = 0.2, the contribution of X_M to the total adsorbed water was 69.7% and at the same conditions achieved 73.7% and 84.2% in the case of P and 50D alginates. The X_M contribution decreased with increasing a_w (i.e., at a_w = 0.4, 59.1, 63.5 and 76.4% for S, P and 50D alginates, respectively). As example, Figure 5 shows the X_M and X_G contributions to the total equilibrium moisture content of 50D alginate at 20 and 50°C. An acceptable agreement can be observed between the water sorption isotherm fitted by Halsey model and the proposed model given by Equation (12).

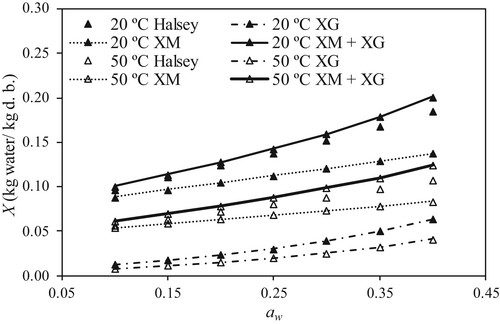
Shimanuki et al. (2020) demonstrated that, at very low moisture content, helical structures formed by short molecular chains present in alginates are composed exclusively of G blocks. Therefore, under these conditions, the surface of G units was not completely available to adsorb water so easily as M units. The 50D alginate was the tested sample with the highest amount of M units (M/G = 1.21) and S the lowest (M/G = 0.91), but P showed a M/G (1.15) closer 50D. It seems that exclusively the relative amount of G is not enough to explain these differences. Nevertheless, S alginate contained a greater number of diads F_GG (0.35) and triads F_GGG (0.30) than P (0.23 and 0.13) and 50D (0.20 and 0.10) alginates. This fact could explain the existence of more helical structures formed by G blocks in S alginate and the contribution of X_G to total adsorbed water consequently decreased. Helical structures were progressively disappearing with water adsorption (higher a_w values) and the contribution of X_G increased with the creation of new available surfaces.

4 CONCLUSIONS

No significant differences were found between tested commercial alginates, and processed alginate was the most hygroscopic one. Halsey model was chosen to fit adequately for describing experimental desorption isotherm data for several alginates in the temperature range from 25 to 50°C. The differential enthalpy and entropy of sorption for all samples decreased and increased, respectively, exponentially with increasing moisture content to 0.15–0.20 kg/kg d.b., then decreased slowly to near zero at higher moisture content, due to a decrease of binding energies between water molecules and sorption sites with increasing moisture content. Integral enthalpy and entropy showed respective maximum and minimum values in the interval from 0.15 to 0.20 kg/kg d.b. Alginates must be dried up to this moisture content to achieve optimum stability during storage. A model based on the structural features of alginate was proposed and satisfactorily tested to predict the equilibrium moisture content of alginates at low water activity values (<0.4). Mannuronate, M, was more hygroscopic than guluronate, G, and consequently, a higher amount of M in the alginate increases its hygroscopicity. Nevertheless, the presence of helical structures formed by G blocks must be also considered in a more complex structural model.

AUTHOR CONTRIBUTIONS

Leticia Montes: Conceptualization; Data curation; Formal analysis; Investigation; Validation; Methodology; Writing—original draft. Mauro Gisbert: Formal analysis; Validation; Writing—review & editing. Ramón Moreira: Conceptualization; Methodology; Writing—review & editing; Project administration; Supervision; Funding acquisition.

FUNDING INFORMATION

Authors acknowledge the financial support of the Spanish Ministry of Science and Innovation (Project RTI2018-095919-B-C2) and the European Regional Development Fund (FEDER) and Xunta de Galicia (Consolidation Project ED431B 2019/01).

CONFLICT OF INTEREST

The authors declared no conflicts of interest for this article.

Open Research

DATA AVAILABILITY STATEMENT

Data available on request due to privacy/ethical restrictions.

REFERENCES

Abka-Khajouei, R., Tounsi, L., Shahabi, N., Patel, A. K., Abdelkafi, S., & Michaud, P. (2022). Structures, properties and applications of alginates. Marine Drugs, 20, 364. https://doi.org/10.3390/md20060364
10.3390/md20060364
CAS PubMed Web of Science® Google Scholar
Adamczak, M. I., Martinsen, Ø. G., Smistad, G., & Hiorth, M. (2017). Polymer coated mucoadhesive liposomes intended for the management of xerostomia. International Journal of Pharmaceutics, 527, 72–78. https://doi.org/10.1016/j.ijpharm.2017.05.032
10.1016/j.ijpharm.2017.05.032
CAS PubMed Web of Science® Google Scholar
Brunauer, S., Deming, L. S., Deming, W. E., & Teller, E. (1940). On theory of the van der Waals adsorption of glass. Journal of the American Chemistry Society, 62, 1723–1732. https://doi.org/10.1021/ja01864a025
10.1021/ja01864a025
CAS Web of Science® Google Scholar
Chee, S. Y., Wong, P. K., & Wong, C. L. (2011). Extraction and characterisation of alginate from brown seaweeds (Fucales, Phaeophyceae) collected from Port Dickson, peninsular Malaysia. Journal of Applied Phycology, 23, 191–196. https://doi.org/10.1007/s10811-010-9533-7
10.1007/s10811-010-9533-7
Web of Science® Google Scholar
Fasina, O. O., Ajibola, O. O., & Tyler, R. T. (1999). Thermodynamics of moisture sorption in winged bean seed and gari. Journal of Food Process Engineering, 22, 405–418. https://doi.org/10.1111/j.1745-4530.1999.tb00496.x
10.1111/j.1745-4530.1999.tb00496.x
Web of Science® Google Scholar
Fernando, I. P. S., Lee, W., Han, E. J., & Ahn, G. (2020). Alginate-based nanomaterials: Fabrication techniques, properties, and applications. Chemical Engineering Journal, 391, 123823. https://doi.org/10.1016/j.cej.2019.123823
10.1016/j.cej.2019.123823
CAS Web of Science® Google Scholar
Galus, S., & Lenart, A. (2013). Development and characterization of composite edible films based on sodium alginate and pectin. Journal of Food Engineering, 115, 459–465. https://doi.org/10.1016/j.jfoodeng.2012.03.006
10.1016/j.jfoodeng.2012.03.006
CAS Web of Science® Google Scholar
Halsey, G. (1948). Physical adsorption on non-uniform surfaces. The Journal of Chemical Physics, 16, 931–937. https://doi.org/10.1063/1.1746689
10.1063/1.1746689
CAS Web of Science® Google Scholar
Kaya, K., & Kahyaoglu, T. (2007). Moisture sorption and thermodynamic properties of safflower petals and tarragon. Journal of Food Engineering, 78, 413–421. https://doi.org/10.1016/j.jfoodeng.2005.10.009
10.1016/j.jfoodeng.2005.10.009
Web of Science® Google Scholar
Koksharov, S. A., Aleeva, S. V., Lepilova, O. V., Krichevskii, G. E., & Fidorovskaya, Y. S. (2021). The properties of sodium alginate hydrocolloids upon sorption binding of papain. Colloid Journal, 83, 722–736. https://doi.org/10.1134/S1061933X21060077
10.1134/S1061933X21060077
CAS Web of Science® Google Scholar
Kurek, M., Guinault, A., Voilley, A., Galic, K., & Debeaufort, F. (2014). Effect of relative humidity on carvacrol release and permeation properties of chitosan based films and coating. Food Chemistry, 144, 9–17. https://doi.org/10.1016/j.foodchem.2012.11.132
10.1016/j.foodchem.2012.11.132
CAS PubMed Web of Science® Google Scholar
Lee, K. Y., & Mooney, D. J. (2012). Alginate: Properties and biomedical applications. Progress in Polymer Science, 1, 106–126. https://doi.org/10.1016/j.progpolymsci.2011.06.003
10.1016/j.progpolymsci.2011.06.003
Web of Science® Google Scholar
Madamba, P. S., Driscoll, R. H., & Buckle, K. A. (1996). Enthalpy-entropy compensation models for sorption and browning of garlic. Journal of Food Engineering, 28, 109–119. https://doi.org/10.1016/0260-8774(94)00072-7
10.1016/0260-8774(94)00072-7
Web of Science® Google Scholar
Montes, L., Gisbert, M., Hinojosa, I., Sineiro, J., & Moreira, R. (2021). Impact of drying on the sodium alginate obtained after polyphenols ultrasound-assisted extraction from Ascophyllum nodosum seaweeds. Carbohydrate Polymers, 272, 118455. https://doi.org/10.1016/j.carbpol.2021.118455
10.1016/j.carbpol.2021.118455
CAS PubMed Web of Science® Google Scholar
Moreira, R., Chenlo, F., Sineiro, J., Sánchez, M., & Arufe, S. (2016). Water sorption isotherms and air drying kinetics modelling of brown seaweed Bifurcaria bifurcata. Journal of Applied Phycology, 28, 609–618. https://doi.org/10.1007/s10811-015-0553-1
10.1007/s10811-015-0553-1
CAS Web of Science® Google Scholar
Moreira, R., Chenlo, F., & Torres, M. D. (2009). Simplified algorithm for the prediction of water sorption isotherms of fruits, vegetables and legumes based on chemical composition. Journal of Food Engineering, 94, 334–343. https://doi.org/10.1016/j.jfoodeng.2009.03.026
10.1016/j.jfoodeng.2009.03.026
CAS Web of Science® Google Scholar
Moreira, R., Chenlo, F., Torres, M. D., & Prieto, D. M. (2017). Statistical criteria for modelling of water desorption isotherms of sugars. Estimation of sucrose hygroscopic properties from glucose and fructose data. Advances in Food Science and Engineering, 1, 18–27. https://doi.org/10.22606/afse.2017.11003
10.22606/afse.2017.11003
Google Scholar
Moreira, R., Chenlo, F., Torres, M. D., & Vallejo, N. (2008). Thermodynamic analysis of experimental sorption isotherms of loquat and quince fruits. Journal of Food Engineering, 88, 514–521. https://doi.org/10.1016/j.jfoodeng.2008.03.011
10.1016/j.jfoodeng.2008.03.011
Web of Science® Google Scholar
Polachini, T. C., Betiol, L. F. L., Lopes-Filho, J. F., & Telis-Romero, J. (2016). Water adsorption isotherms and thermodynamic properties of cassava bagasse. Thermochimica Acta, 632, 79–85. https://doi.org/10.1016/j.tca.2016.03.032
10.1016/j.tca.2016.03.032
CAS Web of Science® Google Scholar
Qin, Y., Jiang, J., Zhao, L., Zhang, J., & Wang, F. (2018). Applications of alginate as a functional food ingredient. In A. M. Grumezescu & A. M. Holban (Eds.), Biopolymers for food design (pp. 409–429). Academic Press. https://doi.org/10.1016/B978-0-12-811449-0.00013-X
10.1016/B978-0-12-811449-0.00013-X
Google Scholar
Shimanuki, N., Imai, M., & Nagai, K. (2020). Effects of counter cations on the water vapor sorption properties of alginic acid and alginates. Journal of Applied Polymer Science, 137, 49326. https://doi.org/10.1002/app.49326
10.1002/app.49326
CAS Web of Science® Google Scholar
Shivhare, U. S., Arora, S., Ahmed, J., & Raghavan, G. S. V. (2004). Moisture adsorption isotherms for mushroom. LWT-Food Science and Technology, 37, 133–137. https://doi.org/10.1016/S0023-6438(03)00135-X
10.1016/S0023-6438(03)00135-X
CAS Web of Science® Google Scholar
Xiao, Q., & Tong, Q. (2013). Thermodynamic properties of moisture sorption in pullulan-sodium alginate based edible films. Food Research International, 54, 1605–1612. https://doi.org/10.1016/j.foodres.2013.09.019
10.1016/j.foodres.2013.09.019
CAS Web of Science® Google Scholar
Zhang, H., Bai, Y., Zhao, X., & Duan, R. (2016). Water desorption isotherm and its thermodynamic analysis of glutinous rice flour. American Journal of Food Technology, 11, 115–124. https://doi.org/10.3923/ajft.2016.115.124
10.3923/ajft.2016.115.124
CAS Google Scholar

Citing Literature

All articles

Water sorption isotherms of different sodium alginates: Thermodynamic evaluation and influence of mannuronate-guluronate copolymers