The analysis of plastic loosening zone of tunnels with cold condition, high in situ stress, and weak stratum is the key scientific problem of tunnel construction in cold areas. Based on the unified strength theory and considering the coupling effect of high in situ stress and low-temperature field, the analytical model of the plastic loosening zone of tunnel surrounding rocks was proposed, and the influence laws of physical parameters (initial ground stress, freezing temperature, excavation radius, and intermediate principal stress) was explored. The results illustrate that: (1) with the coupling of low temperature and stress fields, the in-situ stress has a more significant effect on the radius of the plastic loosening zone of the tunnel surrounding rocks, showing a nonlinear correlation. When the in situ stress is small, the influence of the temperature field on the radius of the plastic loosening zone is more obvious. (2) The radius of the plastic loosening zone of the tunnel surrounding rocks increases synchronously with the excavation radius and gradually decreases with the increase of the intermediate principal stress. (3) The greater the temperature difference in the low-temperature field, the tunnel stability has a more significant response to the intermediate principal stress and is positively correlated with the coefficient of the intermediate principal stress. (4) In the actual project, the proposed model can well describe the mechanical behavior and deformation characteristics of tunnel surrounding rocks in low-temperature environment, showing applicability. The research results are expected to provide a theoretical basis for the study of tunnel stability in cold areas.

1 INTRODUCTION

In the construction of major projects in the high cold region of the plateau, the coupling effect of high in situ stress and high cold freeze-thaw poses a challenge to the projects and causes many disasters. The disasters in high in situ stress environment are rock bursts, collapses, and large deformations (Cao, Xia, et al., 2024; Li, 2023, 2024; Zhao & Dai, 2023; Zuo et al., 2024). In cold areas with large temperature difference, engineering disasters such as freezing damage and aggravation of surrounding rock deformation are manifested (Wang, Xu, et al., 2024; Xia et al., 2020; Yang et al., 2023; Zeng et al., 2024; Zhao et al., 2020). Therefore, the study on the development, distribution, and stress state of plastic loosening zone of tunnel surrounding rocks with the coupling effect of low temperature and stress fields can provide positive significance for engineering design and safety construction.

Up to now, the methods for determining the radius of the loosening zone of tunnel surrounding rocks can be summarized into three categories: field test, theoretical calculation, and numerical simulation (Huang et al., 2018; Wang et al., 2022; Yang et al., 2022; Zhang et al., 2023, 2024; Zhu et al., 2021). The completion of the loosening zone is affected by many factors, such as stratigraphic lithology, stress development, and rock mass structural characteristics, so the cultivation process takes a long time. Due to time and practical operation, field tests and numerical simulation are limited in the study of tunnel surrounding rock loosening zone. The theoretical calculation method is efficient and accurate, and has been applied to the study of tunnel stability by many scholars (Chen et al., 2019; Kolawole et al., 2023; Yu et al., 2021; Zhang et al., 2021). Based on the unified strength theory, Yu et al. (2018) improved the double-shear unified strength theory, and then obtained the radius analytic expression involving the parameters of tunnel surrounding rock stress, tunnel wall displacement, and loosening zone radius. Li et al. (2019) conducted field tests on the evolution law of the fracture zone range of tunnel surrounding rocks by the digital speckle method (DSM), revealing the distribution characteristics of the tunnel volume expansion zone and compression zone. Su et al. (2020) derived the formula for calculating the loosening zone radius of tunnel surrounding rocks under different strength criteria, considering the elastic-plastic behavior of surrounding rocks. Tao et al. (2020) conducted field measurement and numerical simulation of the large deformation loosening zone range of the layered slate tunnel and carried out parameter analysis. Zhu (2022) studied the formation mechanism of the loosening zone in the surrounding rocks of deep-buried layered soft rock tunnel. The loosening zone first appears in the tunnel arch, then develops to both sides, and finally, the loosening range is much larger than other parts. Wu et al. (2023) studied the radius of the loosening zone under a high ground temperature environment and explored the influence of temperature effect on the radius of the loosening zone of surrounding rocks.

In the process of tunnel construction and operation in low-temperature environment, the change laws of the stress field will be more complicated, thus affecting the deformation behavior of surrounding rocks. In view of the study on the range of loosening zone of tunnel surrounding rocks in low-temperature field, Xia et al. (2018) found that the nonuniform freeze-heave property of rocks with unidirectional freezing conditions is the key influencing factor for the difference of freeze-heave force, and put forward a theory to calculate the nonuniform freeze-heave force of surrounding rocks considering the orientation. Huang and Yang (2010) used the H-B criterion to derive the elastic–plastic stress and displacement expressions of circular tunnels considering the effect of osmotic force. Huang et al. (2015) obtained an analytical solution of the loosening zone range of the tunnel surrounding rocks with the conditions of damage and expansion by considering the rock elastic-plastic damage constitutive model and the nonuniform frost heave characteristics. Feng et al. (2019) investigated the elastic-plastic solution based on the D-P criterion and compared the magnitude of frost heave force under different D-P expressions. Gao et al. (2020) derived strain-softened elastoplastic solutions of deep-buried tunnels based on different strength criteria and explored the deformation characteristics of tunnels. In summary, the analytical solution of the loosening zone of tunnel surrounding rocks is mainly aimed at the plastic deformation process with different strength criteria, and the theoretical study under the multi-factor coupling is not in-depth (Dou et al., 2024; Liu et al., 2024; Wang et al., 2023; Wang, Zhou, et al., 2024; Yang et al., 2024).

The objective of this study is to investigate the characteristics of the plastic loosening zone in tunnels passing through weak strata. Based on the unified strength theory and considering the influence of the intermediate principal stress, an analytical model of the plastic deformation of the circular tunnel surrounding rocks with the coupling effect of low temperature and stress fields was established, and the plastic deformation radius and stress evolution law of the soft surrounding rock tunnel were analyzed. This analytical solution takes into account the coupling effect of temperature and stress fields, and can more accurately describe the mechanical behavior of the tunnels under special geological conditions. The accuracy and applicability of this model are verified by practical tunnel engineering cases.

2 TEMPERATURE–STRESS CHARACTERISTICS

The temperature field of the tunnel in the cold area has typical nonequilibrium characteristics, and its distribution has obvious spatial differences and is affected by multiple factors such as formation lithology and groundwater. Therefore, in the study of the plastic loosening zone of tunnel surrounding rocks with the coupled effect of temperature and stress, the following basic assumptions are made about the temperature exchange between the air and the surrounding rock mass in tunnels: (a) The tunnel is a circular horizontal tunnel of infinite length, the radius is expressed as ${r}_{0}$ , the surrounding rock mass is isotropic, and the frost heave coefficients $\xi$ in different directions are consistent. (b) The temperature field in the tunnel is stable, and the radius of the surrounding rock affected by air is ${R}_{0}$ . (c) The air temperature in the tunnel is consistent with the tunnel wall temperature ${T}_{{r}_{0}}$ , and the temperature of the original rock mass is ${T}_{{R}_{0}}$ . (d) The temperature of surrounding rocks changes along the radial direction of the tunnel, and there is no longitudinal temperature difference.

Based on these assumptions, the complex problem of solving the unsteady temperature field is simplified, and the solution of the temperature field distribution of the tunnel surrounding rocks in the cold area is transformed into the thermodynamic conduction problem of the thick-walled cylinder, whose inner radius is ${r}_{0}$ and the outer radius is ${R}_{0}$ . The calculation diagram is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Spatial distribution characteristics of temperature field in cold area.

The differential equation of axisymmetric stable heat conduction is (Cao, Zhang, et al., 2024):

\frac{{d}^{2}T(r)}{d{r}^{2}}+\frac{1}{r}\frac{dT(r)}{dr}=0.

()

The boundary conditions are:

\left\{\begin{array}{c}r={r}_{0},T({r}_{0})={T}_{{r}_{0}}\\ r={R}_{0},T({R}_{0})={T}_{{R}_{0}}\end{array}\right.,

()

where

{r}_{0}

denotes tunnel radius (m),

{T}_{{r}_{0}}

and

{T}_{{R}_{0}}

are tunnel wall and primary rock temperatures (°C), respectively,

{R}_{0}

is cryogenic freezing zone radius, and

r

is the radius from the tunnel center to any point in the surrounding rocks (m).

Then, the variation law of the temperature field in the tunnel surrounding rocks is obtained as follows:

T(r)={T}_{{r}_{0}}+({T}_{{R}_{0}}-{T}_{{r}_{0}})\frac{\mathrm{ln}(r/{r}_{0})}{\mathrm{ln}({R}_{0}/{r}_{0})}.

()

There is a temperature gradient along the radial direction of the tunnel in the cold region, and the temperature difference will produce temperature stress, and the greater the temperature difference, the greater the temperature stress. The influence of temperature on in situ stress can be expressed as:

{\sigma }_{T}=\xi ET.

()

By substituting Equation (3) into (4), the temperature stress of tunnel surrounding rocks

{\sigma }_{T}

can be obtained as follows:

{\sigma }_{T}=\xi E\left[{T}_{{r}_{0}}+({T}_{{R}_{0}}-{T}_{{r}_{0}})\frac{\mathrm{ln}(r/{r}_{0})}{\mathrm{ln}({R}_{0}/{r}_{0})}\right],

()

where

\xi

denotes frost heave coefficient (1/°C), and

E

is the elastic modulus of tunnel surrounding rocks, which is obtained by the indoor rock tests and conversion.

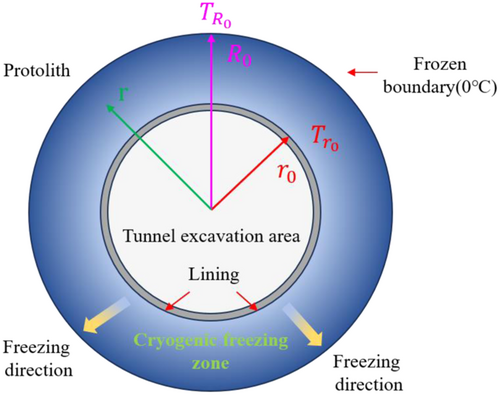
3 ANALYTICAL CALCULATION OF RADIUS IN PLASTIC LOOSENING ZONE

3.1 Plastic loosening zone

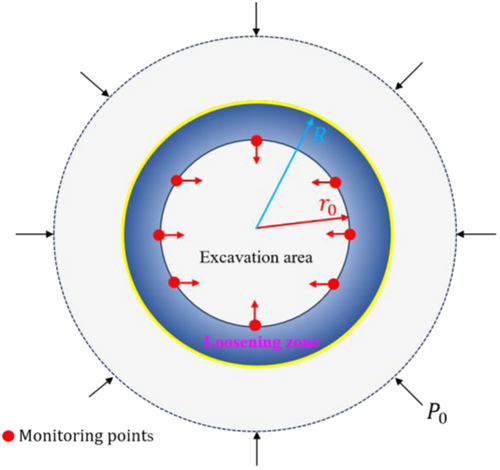
The stress redistribution of the tunnel surrounding rocks after excavation with ideal elastic-plastic stress state can be divided into three parts: the initial in situ stress zone, the elastic zone, and the plastic zone, wherein the plastic zone includes the loosening zone and the plastic zone (Wu et al., 2023). Based on the unified strength theory, this study analyzes the mechanical characteristics of the loosening zone of surrounding rocks. The circumferential stress of the loosening zone is less than the in-situ stress (Figure 2). It is assumed that the circular tunnel in the cold area is located in the infinite elastic body, the radius of the loosening circle is $R$ , the elastic parameters of the surrounding rock are $E$ and $\mu$ , the cohesion force and internal friction Angle of the surrounding rock are divided into $c$ and $\varphi$ , and the supporting stress is ${P}_{i}$ .

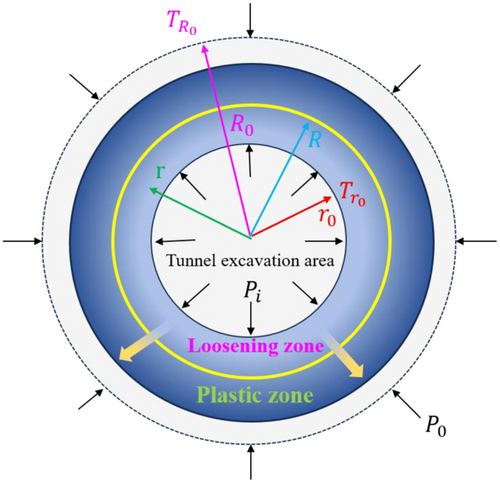
3.2 Stress field of tunnel surrounding rocks

Existing studies have shown that the spatio-temporal distribution of elastoplastic stress in surrounding rocks has obvious differences during tunnel excavation and support, resulting in different characteristics of the plastic loosening zone of surrounding rocks (Liang et al., 2024; Liu & Wang, 2024). This paper mainly investigates the change rule and influence range of plastic loosening zone of surrounding rocks after tunnel excavation. The unified strength theory makes up the defect that the influence of intermediate principal stress is not considered in the calculation of surrounding rock stress (Hong et al., 2024; Zhao et al., 2023), taking cohesion and internal friction Angle as material strength parameters, obtained the expression of the unified strength theory under plane strain state (Lv et al., 2023) as follows:

\frac{{\sigma }_{1}-{\sigma }_{3}}{2}=\frac{{\sigma }_{1}+{\sigma }_{3}}{2}\,\sin \,{\varphi }_{t}+{c}_{t}\,\cos \,{\varphi }_{t},

()

\left\{\begin{array}{c}\sin \,{\varphi }_{t}=\displaystyle \frac{2(1+b)\sin \,\varphi }{2+b+b\,\sin \,\varphi }\\ {c}_{t}=\displaystyle \frac{2(1+b)\sin \,\varphi }{2+b+b\,\sin \,\varphi }\cdot \displaystyle \frac{1}{\cos \,{\varphi }_{t}}\\ b=\displaystyle \frac{1+\alpha }{B-1},B=\displaystyle \frac{{\sigma }_{t}}{{\tau }_{s}},{\alpha }^{^{\prime} }=\displaystyle \frac{{\sigma }_{t}}{{\sigma }_{c}}\end{array}\right.,

()

where

{c}_{t}

and

{\varphi }_{t}

are unified cohesion and internal friction Angle, respectively, b is the influence coefficient of intermediate principal stress, which reflects the influence degree of intermediate principal shear stress and corresponding surface normal stress on material damage

0\le b\le 1

{\alpha }^{^{\prime} }

is the compressive strength ratio of the material, B is the tensile shear strength ratio of the material,

{\sigma }_{c}

{\sigma }_{t}

, and

{\tau }_{s}

are the compressive strength, tensile strength and shear strength (MPa) of rocks, respectively.

According to the existing research results, the tunnel excavation process belongs to the shrinkage hole problem in which the support stress

{P}_{i}

is less than the initial ground stress

{P}_{0}

. The radial stress and circumferential stress are assumed to be

{\sigma }_{r}

and

{\sigma }_{\theta }

respectively. The redistribution of stress after unloading causes the surrounding rock of the tunnel to produce plastic failure within a certain range, when

{\sigma }_{\theta }\gt {\sigma }_{r}

, that is, the first principal stress is the circum-axial stress (Chang et al., 2024; Li et al., 2024; Zhang et al., 2020). Then

{\sigma }_{1}={\sigma }_{\theta }

{\sigma }_{3}={\sigma }_{r}

, and Equation (6) is expressed as:

\frac{{\sigma }_{\theta }-{\sigma }_{r}}{2}=\frac{{\sigma }_{\theta }+{\sigma }_{r}}{2}\,\sin \,{\varphi }_{t}+{c}_{t}\,\cos \,{\varphi }_{t}.

()

Then,

{\sigma }_{r}-{\sigma }_{\theta }=-\frac{2\,\sin \,{\varphi }_{t}}{1-\,\sin \,{\varphi }_{t}}{\sigma }_{r}-\frac{2{c}_{t}\,\sin \,{\varphi }_{t}}{1-\,\sin \,{\varphi }_{t}}.

()

Considering the influence of temperature stress and ignoring the volume force, the equilibrium differential equation in the plastic zone of tunnel surrounding rock can be captured as (Chen & Yu, 2024; Lyu et al., 2020):

\frac{d{\sigma }_{r}}{dr}+\frac{d{\sigma }_{T}}{dr}+\frac{{\sigma }_{r}-{\sigma }_{\theta }}{r}=0.

()

Substitute Equation (5) into Equations (9) and (10), and according to the boundary condition

{\sigma }_{r}{|}_{r={r}_{0}}={P}_{i}

, the calculation formula of radial and circumferential stress in the plastic zone can be obtained:

\begin{array}{c}{\sigma }_{r}=({P}_{i}+M){(\displaystyle \frac{r}{{r}_{0}})}^{\displaystyle \frac{2\sin {\varphi }_{t}}{1-\sin {\varphi }_{t}}}-M\\ {\sigma }_{\theta }=\displaystyle \frac{1+\,\sin \,{\varphi }_{t}}{1-\,\sin \,{\varphi }_{t}}{\sigma }_{r}+\displaystyle \frac{2{c}_{t}\,\sin \,{\varphi }_{t}}{1-\,\sin \,{\varphi }_{t}},\end{array}

()

where

M

is a constant related to unity of cohesion

{c}_{t}

, unity of internal friction Angle

{\varphi }_{t}

, frost heave coefficient per unit temperature

\xi

, elastic modulus E, primary rock temperature

{T}_{{R}_{0}}

, tunnel wall temperature

{T}_{{r}_{0}}

, tunnel excavation radius

{r}_{0}

, and low-temperature freezing zone radius

{R}_{0}

M={c}_{t}\,\cot \,{\varphi }_{t}-\frac{\xi E({T}_{{R}_{0}}-{T}_{{r}_{0}})(1-\,\sin \,{\varphi }_{t})}{2\,\sin \,{\varphi }_{t}\,\mathrm{ln}\,\frac{{R}_{0}}{{r}_{0}}}.

()

3.3 Calculation of loosening zone radius

The radius of the plastic loosening zone after tunnel excavation is of key significance to the design of tunnel support structure, so this paper focuses on its calculation method. Existing research results (Duan et al., 2023; Xia et al., 2018) show that the circum-axial stress

{\sigma }_{\theta }

in the plastic loosening zone of surrounding rocks is always less than or equal to the initial ground stress

{P}_{0}

, that is, when

r=R

{\sigma }_{\theta }={P}_{0}

, substituting it into Equation (12):

{P}_{0}=\frac{1+\,\sin \,{\varphi }_{t}}{1-\,\sin \,{\varphi }_{t}}\left[({P}_{i}+M){(\frac{R}{r})}^{\frac{2\sin {\varphi }_{t}}{1-\sin {\varphi }_{t}}}-M\right]+\frac{2{c}_{t}\,\cot \,{\varphi }_{t}}{1-\,\sin \,{\varphi }_{t}}.

()

Then, the formula for calculating the radius of the plastic loosening zone of surrounding rocks with the coupling effect of low temperature and stress is as follows:

R={r}_{0}\frac{({P}_{0}-\frac{2{c}_{t}\,\cot \,{\varphi }_{t}}{1-\,\sin \,{\varphi }_{t}})\frac{1+\,\sin \,{\varphi }_{t}}{1-\,\sin \,{\varphi }_{t}}+M}{{P}_{i}+M}.

()

To facilitate the analysis of the influence of different parameters on the radius of plastic loosening zone of surrounding rocks, Lamme's formula is used to approximate the calculation of support stress. Assuming that the tunnel wall lining thickness is t and the tunnel wall pressure is 0 MPa, then:

{P}_{i}={\sigma }_{r}{|}_{r={r}_{0}+t}=\frac{1-\frac{{r}_{0}^{2}}{{({r}_{0}+t)}^{2}}}{1-\frac{{r}_{0}^{2}}{{R}_{0}^{2}}}.

()

By substituting Equation (15) into (14), the theoretical calculation formula of plastic loosening zone radius R of surrounding rocks with the coupling effect of low temperature and stress can be obtained:

R={r}_{0}{\left[\frac{({P}_{0}-\frac{2{c}_{t}\cot {\varphi }_{t}}{1-\sin {\varphi }_{t}})\frac{1+\sin {\varphi }_{t}}{1-\sin {\varphi }_{t}}+M}{\left(1-\frac{{r}_{0}^{2}}{{({r}_{0}+t)}^{2}}\right)/(1-\frac{{r}_{0}^{2}}{{R}_{0}^{2}}){P}_{0}+M}\right]}^{\frac{1-\sin {\varphi }_{t}}{2\sin {\varphi }_{t}}}.

()

According to the definition of the formula for calculating the radius of the plastic loosening zone, the formulas (14) and (16) should meet the requirements of

R/r\gt 1

. If

R/r\le 1

, the surrounding rock is in an elastic state, and the formula is no longer applicable. Then:

{P}_{i}\lt ({P}_{0}-\frac{2{c}_{t}\,\cot \,{\varphi }_{t}}{1-\,\sin \,{\varphi }_{t}})\frac{1+\,\sin \,{\varphi }_{t}}{1-\,\sin \,{\varphi }_{t}}.

()

By substituting Equation (15) into (17), the in situ stress of surrounding rocks when plastic failure occurs should meet:

{P}_{0}\gt \frac{\frac{2{c}_{t}\,\cot \,{\varphi }_{t}}{1-\,\sin \,{\varphi }_{t}}}{\frac{1+\,\sin \,{\varphi }_{t}}{1-\,\sin \,{\varphi }_{t}}-\frac{1-\frac{{r}_{0}^{2}}{{({r}_{0}+t)}^{2}}}{1-\frac{{r}_{0}^{2}}{{R}_{0}^{2}}}}.

()

4 PARAMETER ANALYSIS

4.1 Tunnel parameters

Based on the water diversion tunnel under construction in a hydropower station in Xizang, this paper analyzes the complex geological problems encountered in the actual construction process, such as low temperature environment and high ground stress. According to the investigation report of the tunnel, the strata are mainly basalt, slate, limestone, siltstone and mudstone interlayers, etc. This study discusses the weak strata. The cross-section of the tunnel is circular, the buried depth is about 1000 m, the tunnel excavation radius r₀ = 6 m, the temperature of the original rock mass T_R0 = −12.4°C, and the temperature of the tunnel wall T_r0 = 0°C, then the difference between the temperature of the original rock mass and the temperature of the tunnel wall $\bigtriangleup$ T = 12.4°C.

Combined with relevant data (Xia et al., 2018, 2020), the influence coefficient of intermediate principal stress b = 0.2, influence radius of low temperature freezing zone R₀ = 10r₀, lining thickness t = 0.50 m, and in situ stress is calculated according to the self-weight stress. The parameters required by the theoretical calculation formula of other physical parameters of surrounding rocks are as follows (Table 1).

Table 1. Tunnel parameters.

E/MPa	μ	P₀/MPa	r₀/m	Intermediate principal stress coefficient b
Elasticity modulus	Poisson's ratio	In situ stress	Tunnel radius
3900	0.30	26	6	0.2
Cohesion c/MPa	Internal friction angle φ/°	Frost heaving coefficient per unit temperature ξ/(1/°C)	Temperature difference $\bigtriangleup$ T/°C	Volume-weight w/(kN/m³)
0.52	39	0.000045	12.4	25.4

4.2 Loosening zone characteristic

4.2.1 Influence of in situ stress and temperature difference

The tunnel parameters (Table 1) are substituted into Equations (7) and (18). When the initial ground stress is satisfied, the surrounding rock will produce plastic failure. Equation (16) was used to calculate the radius of the loosening ring, analyze the parameters, and draw the influence curve. By substituting tunnel parameters (Table 1) into Equations (7) and (18), plastic failure of surrounding rocks occurs when the in-situ stress is satisfied. Equation (16) was used to calculate the radius of the loosening zone, analyze the parameters, and draw the influence curves (Figures 3 and 4).

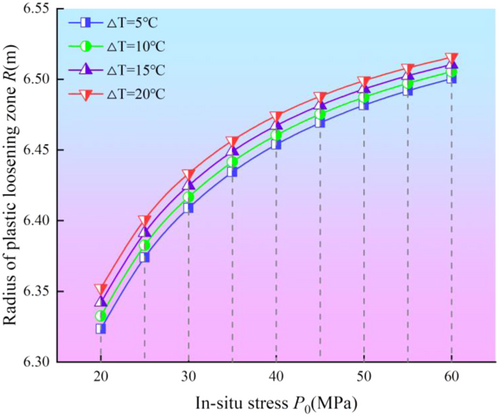
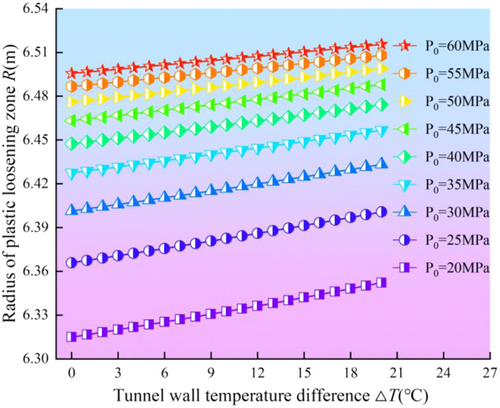
The results show that: (1) With the coupling effect of low temperature and stress, the radius of the plastic loosening zone increases with the increase of the in situ stress and the temperature difference between the rock mass and the tunnel wall. (2) Taking $\bigtriangleup$ T = 5°C, when increasing from 20 to 60 MPa, the radius R of plastic loosening zone of tunnel surrounding rocks increases from 6.32348 to 6.50044 m, increasing by 0.17696 m. Taking P₀ = 20 MPa, when $\bigtriangleup$ T increases from 5°C to 20°C, the radius of plastic loosening zone increases from 6.32348 to 6.352323 m, increasing by 0.02875 m. With the coupling effect of low temperature and stress, the influence of in situ stress on the radius of the plastic loosening zone is more significant than that of temperature difference. (3) When the local stress is 20 Mpa < P₀ < 60 MPa, the plastic loosening zone radius increases gradually with the ground stress increasing, but the growth rate is first fast and then slow. Therefore, the more sensitive change of the tunnel surrounding the rock plastic loosens the zone with smaller ground stress.

Figures 4 and 5 show that: (1) With the increase of temperature difference at low temperature, the radius of plastic loosening zone of surrounding rocks shows an approximate linear increase trend. When P₀ = 20 MPa, $\bigtriangleup$ T increased from 0°C to 20°C, R increased from 6.314909 m to 6.352230 m, an increase of 0.0373207 m, or 0.59%. When P₀ = 60 MPa, $\bigtriangleup$ T increased from 0°C to 20°C, R increased from 6.495613 to 6.515519 m, an increase of 0.31%. (2) The influence of in-situ stress on the radius of plastic loosening zone of tunnel surrounding rocks is aggravated by the existence of a low-temperature field.

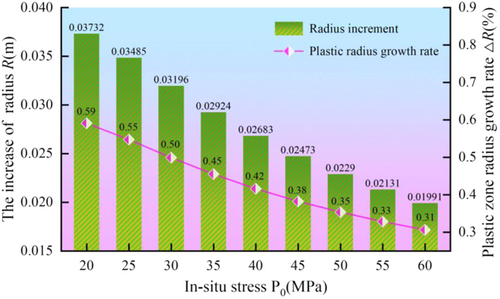
At low temperature, the surrounding rock mineral composition produces a differential frost heave effect, and the void structure between mineral components changes, which leads to the surrounding rock mechanical properties deterioration. Under the action of stress, the expansion rate of the void between mineral components increases, which aggravates the surrounding rock's mechanical properties deterioration at low temperature.

4.2.2 Tunnel radius and intermediate principal stress coefficient

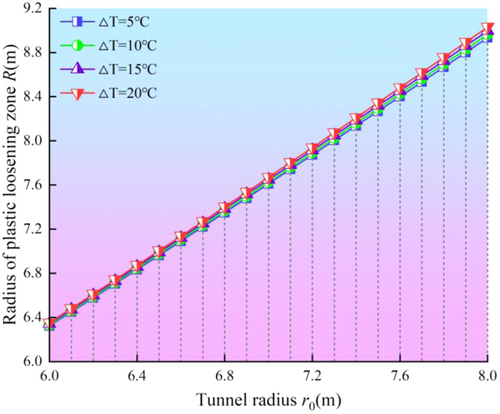
Figure 6 shows that the radius of the plastic loosening zone increases approximately linearly with the increase of the tunnel radius under the coupling effect of low temperature-stress. When the in situ stress P₀ = 20 MPa, the larger the temperature difference, the larger the radius of the loosening zone.

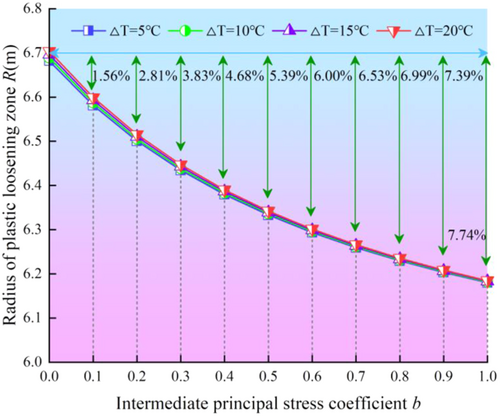
The radius of the plastic loosening ring decreases with the increase of the intermediate principal stress coefficient, and the decrease is 7.74%, which indicates that the stability of the surrounding rock is positively correlated with the intermediate principal stress coefficient. At the same time, the change rate of the radius of the plastic loosening ring gradually decreases with the increase of the intermediate principal stress coefficient, and the influence of the sensitivity of the intermediate principal stress coefficient on the stability of surrounding rock gradually decreases (Figure 7). (1) Taking P₀ = 20 MPa, ΔT = 5°C, and when b increases from 0 to 1.0, the radius R of the plastic relaxation zone of the tunnel surrounding rocks decreases from 6.668179 to 6.180018 m, a decrease of 0.501770 m, a decrease of about 7.51%. (2) Taking P₀ = 20 MPa and ΔT = 10°C, when b increases from 0 to 1.0, the radius R of the plastic loosening zone of the tunnel surrounding rocks decreases from 6.688984 to 6.181543 m, a decrease of 0.507442 m, a decrease of about 7.59%. (3) Taking P₀ = 20 MPa and ΔT = 15°C, when b increases from 0 to 1.0, the radius R of the plastic loosening zone of tunnel surrounding rocks decreases from 6.696335 m to 6.183093 m, decreasing by 0.513243 m, or about 7.66%. (4) Taking P₀ = 20 MPa and ΔT = 20°C, when b increases from 0 to 1.0, the radius R of the plastic loosening zone of tunnel surrounding rocks decreases from 6.703847 to 6.184670 m, decreasing by 0.519177 m, or about 7.74%. It shows that the influence of the intermediate principal stress coefficient on the radius of the plastic loosening zone is slight, but the greater the temperature difference at low temperature, the greater the influence of the intermediate principal stress coefficient on the radius of the plastic loosening zone. At the same time, the change of intermediate principal stress coefficient b is related to tensile strength, shear strength, and compressive strength. When b increases, the tensile strength, compressive strength, and shear strength increase, and the deformation of the surrounding rock decreases. When the temperature difference ΔT increases, the tensile, compressive, and shear strength decreases, and the deformation of surrounding rock increases.

5 CASE STUDY

The Dabanshan Tunnel in Qinghai province, with an altitude of 3750 m, has an annual average temperature of −3.2°C, an annual minimum temperature of −15.3°C and an extreme minimum temperature of −34°C. Surrounding rock cracks are developed and pore water is basically saturated. The surrounding rock of monitoring section K106+400 is mainly schist, the maximum freezing depth is 2.10 m, and the maximum tunnel burial depth is 1085 m. According to the in situ ground temperature and stress testing and inversion results, the minimum temperature of the original rock mass in the study section is −15.1°C, the horizontal in situ stress is 24.58 MPa, the vertical in situ stress is 30.72 MPa, and the tunnel excavation radius is 4.55 m. Assuming that the tunnel wall temperature is 0°C, the temperature difference between the original rock mass and tunnel wall $\bigtriangleup$ T = 15°C. Take the middle principal stress coefficient b = 0.20, and the radius of variable temperate zone action R₀ = 10r₀. Other physical parameters of the tunnel surrounding rocks are shown in Table 2.

Table 2. Dabanshan tunnel parameters.

Elasticity modulus	Poisson's ratio	Cohesion	Internal friction angle
E/MPa	μ	c/MPa	φ/°
3100	0.2	0.68	38

Support stress P_i/MPa	Volume-weight w/(kN/m³)	Frost heaving coefficient per unit temperature ξ/(1/°C)	–
0.50	28.31	0.000045	–

To master the deformation characteristics of the surrounding rock and keep the stability of the free surface during tunnel excavation, monitoring points were arranged at the key points of the tunnel (Figure 8). According to the tunnel data, the maximum thickness of the plastic loosening zone of surrounding rocks is 0.35 m, and the minimum thickness is 0.12 m, that is, the radius R of the loosening zone is 4.67–4.90 m. The radius of the plastic loosening zone of the tunnel was calculated by substituting the physical parameters of surrounding rocks with the Equation (16), and compared with the test results and the calculation results without considering the temperature effect (Table 3).

Table 3. Comparison of field measurement and calculation results.

Methods	Construction state	Plastic loosening zone radius R/m
Methods	Construction state	Horizontal direction	Vertical direction
Theoretical calculation	High in situ stress	4.56	4.61
Theoretical calculation	High in situ stress + low temperature	4.69	4.83
Field measurement	High in situ stress + low temperature	4.67	4.90

As shown in Table 3: (1) Calculated based on the unified strength criterion, the radius of the plastic loosening zone under the coupling effect of low temperature and stress is larger than that under the condition of single stress field, with a horizontal difference of 0.13 m and a vertical difference of 0.22 m. The temperature field has a significant influence on the radius of the plastic loosening zone of tunnel surrounding rocks. (2) Under the coupling effect of low temperature and stress, the radius of the surrounding rock loosening zone calculated based on the unified strength criterion is close to the field measured results.

The calculated radius of the horizontal plastic loosening zone is 4.69 m, which is 0.02 m lower than the field measured result of 4.67 m, and the calculated radius of the vertical plastic loosening zone is 4.83 m, which is 0.07 m lower than the field measured result of 4.90 m. The comparison between the calculated and measured results shows that the analytical solution of the radius of the plastic loosening zone based on the unified strength criterion with the coupling effect of low temperature and stress is reasonable, which can better describe the mechanical behavior and deformation laws of the tunnel surrounding rocks in low-temperature environment.

6 CONCLUSIONS

Based on the unified strength theory, combined with the characteristics of tunnel temperature field and high ground stress in low-temperature environment, this study proposes a calculation method for the radius of plastic loosening zone of tunnel surrounding rocks, establishes a theoretical calculation model, and discusses the influence laws of parameters. The applicability of this model is verified by comparing the calculation results with the actual tunnel field measured results, and the following conclusions are drawn.

1.
With the coupling effect of low temperature and stress, the radius of the plastic loosening zone increases gradually with the increase of the in situ stress and temperature difference. The influence of the in situ stress on the radius of the loosening zone is mainly nonlinear correlation.
2.
With the coupling effect of low temperature and stress, the radius of the plastic loosening zone and the excavation radius show an approximate linear increase trend and gradually decrease with the increase of the intermediate principal stress coefficient.
3.
The difference between the results obtained by the proposed method and the measured results is slight, which proves that the calculation model can describe the mechanical behavior and deformation laws of tunnel-surrounding rocks well in low-temperature environment.

ACKNOWLEDGMENTS

This work was supported by the Postdoctoral Fellowship Program of CPSF under Grant Number GZC20240167, the Chengdu University of Technology Postgraduate Innovative Cultivation Program (CDUT2022BJCX007), and this research was also financially supported by the Huzhou Key Laboratory Fund (HGB23E002).

ETHICS STATEMENT

None declared.

Open Research

DATA AVAILABILITY STATEMENT

All data generated or analyzed during this study are included within the article.

REFERENCES

Cao, S. P., Xia, C. C., Zhou, S. W., & Kou, J. S. (2024). Analytical solution for frost heave force of cold region tunnel caused by non-uniform frost heave of surrounding rock considering freezing temperature gradient. Journal of Tongji University (Natural Science), 52(03), 360–369. https://doi.org/10.11908/j.issn.0253-374x.22240
10.11908/j.issn.0253-374x.22240
Google Scholar
Cao, W. H., Zhang, X. M., Zhang, Y. E., Liu, B., Wang, Y. S., Zhao, Y., Yin, X. L., & Han, X. (2024). Carbon sink for soil and water conservation and the measurement. China Water and Soil Conservation Science (both in English and Chinese), 22(01), 1–11. https://doi.org/10.16843/j.sSWC.2023113
10.16843/j.sSWC.2023113
Google Scholar
Chang, M. Y., Shen, Y. S., Zhang, X., Wu, Z. Q., Wang, Y. Y., & Huang, H. F. (2024). Analytical solution for longitudinal response of tunnels with consideration of surrounding rock-concrete tangential interaction. Chinese Journal of Rock Mechanics and Engineering, 43(08), 2013–2026. https://doi.org/10.13722/j.cnki.jrme.2024.0106
10.13722/j.cnki.jrme.2024.0106
Google Scholar
Chen, G., & Yu, H. T. (2024). Analytical solution for seismic response of composite tunnel liners with arbitrary section shape and embedded with an isolation layer. Tunnelling and Underground Space Technology incorporating Trenchless Technology Research, 150, 105821. https://doi.org/10.1016/j.tust.2024.105821
10.1016/j.tust.2024.105821
Google Scholar
Chen, Z., He, C., Xu, G., Ma, G., & Yang, W. (2019). Supporting mechanism and mechanical behavior of a double primary support method for tunnels in broken phyllite under high geo-stress: A case study. Bulletin of Engineering Geology and the Environment, 78(7), 5253–5267. https://doi.org/10.1007/s10064-019-01479-1.
10.1007/s10064-019-01479-1
CAS Google Scholar
Dou, B. J., Feng, G. H., Mao, X. Y., Zheng, M. W., Ding, S. L., & Xu, C. J. (2024). Analytical solution of stress and deformation of underlying tunnel caused by adjacent surcharge. Bulletin of Science and Technology, 40(04), 90–95. https://doi.org/10.13774/j.cnki.kjtb.2024.04.015
10.13774/j.cnki.kjtb.2024.04.015
Google Scholar
Duan, J., Xia, C., Zhou, S., & Cao, S. (2023). Analytical solution for the temperature field of cold region tunnels that considers thermal resistance. Cold Regions Science and Technology, 215, 103984. https://doi.org/10.1016/j.coldregions.2023.103984
10.1016/j.coldregions.2023.103984
Google Scholar
Feng, Q., Fu, S., Wang, C., Liu, W., Wang, Y., & Qiao, W. (2019). Analytical elasto-plastic solution for frost force of cold-region tunnels considering anisotropic frost heave in the surrounding rock. KSCE Journal of Civil Engineering, 23(9), 3831–3842. https://doi.org/10.1007/s12205-019-1446-7
10.1007/s12205-019-1446-7
Google Scholar
Gao, Y. T., Liang, P., & Zhou, Y. (2020). Strength criterion effect on elastic-plastic solution of deep tunnels considering strain softening characteristics. Journal of Central South University (Science and Technology), 51(09), 2525–2537. https://doi.org/10.11817/j.issn.1672-7207.2020.09.018
10.11817/j.issn.1672-7207.2020.09.018
Google Scholar
Hong, Z. Q., Fu, S. R., Hu, X. D., & Wang, B. S. (2024). Analytical solution for temperature field of artificial ground freezing induced by adiabatic boundary. Journal of Tongji University (Natural Science), 52(05), 749–758. https://doi.org/10.11908/j.issn.0253-374x.22320
10.11908/j.issn.0253-374x.22320
Google Scholar
Huang, F., & Yang, X. L. (2010). Analytical solution of circular openings subjected to seepage in Hoek-Brown media. Rock and Soil Mechanics, 31(05), 1627–1632. https://doi.org/10.3969/j.issn.1000-7598.2010.05.048
10.3969/j.issn.1000-7598.2010.05.048
Google Scholar
Huang, J. H., Xia, C. C., Han, C. L., & Huang, M. (2015). Analytical solution of frost heave force acting on cold-region tunnel liner considering anisotropy frost heave of surrounding rock. Chinese Journal of Rock Mechanics and Engineering, 34(S2), 3766–3774. https://doi.org/10.13722/j.cnki.jrme.2014.0830
10.13722/j.cnki.jrme.2014.0830
Google Scholar
Huang, S. B., Liu, Q. S., Liu, Y. Z., & Cheng, A. P. (2018). Frost heaving pressure and characteristics of frost cracking in elliptical cavity (crack) of rock mass under coupled thermal-mechanical condition at low temperature. Chinese Journal of Geotechnical Engineering, 40(03), 459–467. https://doi.org/10.11779/CJGE201803009
10.11779/CJGE201803009
Google Scholar
Kolawole, O., Assaad, R. H., Adams, M. P., Ngoma, M. C., Anya, A., & Assaf, G. (2023). Coupled experimental assessment and machine learning prediction of mechanical integrity of MICP and cement paste as underground plugging materials. Bio-Geotechnics, 1(2), 100020. https://doi.org/10.1016/J.BGTECH.2023.100020
10.1016/J.BGTECH.2023.100020
Google Scholar
Li, G. Y. (2023). Thoroughly implement the spirit of the 20th National Congress of the Communist Party of China and solidly promote the high-quality development of water conservancy in the new stage-speech at the National Water Conservancy Work Conference in 2023. Water Resources Development Research, 23(1), 1–11. https://doi.org/10.13928/j.cnki.wrdr.2023.01.001
10.13928/j.cnki.wrdr.2023.01.001
Google Scholar
Li, G. Y. (2024). Improved water security for China's efforts to build itself into a stronger country and rejuvenate the Chinese nation on all fronts by pursuing Chinese modernization-speech at the 2024 National Water Conservancy Work Conference. Water Resources Development Research, 24(1), 1–10. https://doi.org/10.13928/j.cnki.wrdr.2024.01.001
10.13928/j.cnki.wrdr.2024.01.001
CAS Google Scholar
Li, T., Zheng, K., Peng, H., Zhang, Z., & Liu, B. (2024). Analytical solution for pipeline settlement law using shield tunnel excavation underneath based on Vlasov-Timoshenko model considering lateral soil action. International Journal of Geomechanics, 24(7), 8876. https://doi.org/10.1061/IJGNAI.GMENG-8876
10.1061/IJGNAI.GMENG-8876
Google Scholar
Li, Y. H., Tang, X. J., Yang, S., & Chen, J. W. (2019). Evolution of the broken rock zone in the mixed ground tunnel based on the DSCM. Tunnelling and Underground Space Technology incorporating Trenchless Technology Research, 84, 248–258. https://doi.org/10.1016/j.tust.2018.11.017
10.1016/j.tust.2018.11.017
Web of Science® Google Scholar
Liang, Y., Zhou, F., & Qu, Y. (2024). Semi-analytical solution for seismic response of circular lined tunnel in alpine valley composite site. Computers and Geotechnics, 172, 106475. https://doi.org/10.1016/j.compgeo.2024.106475
10.1016/j.compgeo.2024.106475
Google Scholar
Liu, Q., & Wang, H. N. (2024). Analytical model for tunnel stability and support pressure prediction of viscoelastic-plastic rock masses under the influence of seepage. Journal of Tsinghua University (Science and Technology), 2024, 1–9. https://doi.org/10.16511/j.cnki.qhdxxb.2024.26.023
10.16511/j.cnki.qhdxxb.2024.26.023
Google Scholar
Liu, W., Su, X., Zhang, G., & Chen, D. (2023). Projection of future dry-wet evolution in Northwest China and its uncertainty attribution analysis. River, 2(1), 65–78. https://doi.org/10.1002/rvr2.39
10.1002/rvr2.39
Google Scholar
Lv, Z., Yuan, S., & Lin, H. (2023). Analytical stress solution for cold region tunnels with unequal ground stress and support delay under different frost heave conditions of surrounding rock. Cold Regions Science and Technology, 206, 103742. https://doi.org/10.1016/j.coldregions.2022.103742
10.1016/j.coldregions.2022.103742
Google Scholar
Lyu, Z., Xia, C., & Liu, W. (2020). Analytical solution of frost heaving force and stress distribution in cold region tunnels under non-axisymmetric stress and transversely isotropic frost heave of surrounding rock. Cold Regions Science and Technology, 178, 103117. https://doi.org/10.1016/j.coldregions.2020.103117
10.1016/j.coldregions.2020.103117
Google Scholar
Su, S. L., Gao, H. H., & Zhou, K. L. (2020). Calculation method of roadway surrounding rock loose circle based on unified strength theory. Science Technology and Engineering, 20(27), 11045–11050. https://doi.org/10.3969/j.issn.1671-1815.2020.27.010
10.3969/j.issn.1671-1815.2020.27.010
Google Scholar
Tao, Z. G., Luo, S. L., Li, M. N., Ren, S. L., & He, M. C. (2020). Optimization of large deformation control parameters of layered slate tunnels based on numerical simulation and field test. Chinese Journal of Rock Mechanics and Engineering, 39(03), 491–506. https://doi.org/10.13722/j.cnki.jrme.2019.0841
10.13722/j.cnki.jrme.2019.0841
Google Scholar
Wang, J., Xu, M., Zhang, G., Zhang, T., Wang, D., Zang, H., & Hou, X. (2024). Progress and future of China's aquatic ecological environment protection. River, 3(2), 119–128. https://doi.org/10.1002/rvr2.87
10.1002/rvr2.87
Google Scholar
Wang, Q., Zhou, Y., Ren, S., Wang, P., & Wu, Z. (2024). Analytical study on heat transfer of a tunnel lining-rock-insulation structure in cold regions. Journal of Cold Regions Engineering, 38(1), 1–9. https://doi.org/10.1061/JCRGEI.CRENG-705
10.1061/JCRGEI.CRENG-705
Google Scholar
Wang, S., Li, D. Q., & Du, W. (2022). Recent advances in the investigation of a slow-moving landslide in the Three Gorges Reservoir area. River, 1(1), 91–103. https://doi.org/10.1002/rvr2.8
10.1002/rvr2.8
Google Scholar
Wang, Y. Z., Konstantinou, C., Tang, S. K., & Chen, H. Y. (2023). Applications of microbial-induced carbonate precipitation: A state-of-the-art review. Bio-Geotechnics, 1(1), 100008. https://doi.org/10.1016/J.BGTECH.2023.100008
10.1016/J.BGTECH.2023.100008
Google Scholar
Wu, S. Z., Zeng, M. T., Li, J. Y., & Zhang, L. Z. (2023). Properties of plastic loose circle of surrounding rocks under thermal-force coupling effect. Tunnel Construction, 43(06), 988–994. https://doi.org/10.3973/j.issn.2096-4498.2023.06.009
10.3973/j.issn.2096-4498.2023.06.009
Google Scholar
Xia, C., Lv, Z., Li, Q., Huang, J., & Bai, X. (2018). Transversely isotropic frost heave of saturated rock under unidirectional freezing condition and induced frost heaving force in cold region tunnels. Cold Regions Science and Technology, 152, 48–58. https://doi.org/10.1016/j.coldregions.2018.04.011
10.1016/j.coldregions.2018.04.011
Web of Science® Google Scholar
Xia, C. C., Lv, Z. T., & Wang, Y. C. (2020). Advance and review on frost heaving force calculation methods in cold region tunnels. China Journal of Highway and Transport, 33(05), 35–43. https://doi.org/10.3969/j.issn.1001-7372.2020.05.003
10.3969/j.issn.1001-7372.2020.05.003
Google Scholar
Xia, C. C., Xu, C., Liu, Y. P., & Han, C. L. (2018). Elastoplastic solution of deep buried tunnel considering strain-softening characteristics based on GZZ strength criterion. Chinese Journal of Rock Mechanics and Engineering, 37(11), 2468–2477. https://doi.org/10.13722/j.cnki.jrme.2018.0611
10.13722/j.cnki.jrme.2018.0611
Google Scholar
Yang, Y., Yin, H., Li, M., Liu, W., Li, K., & Yu, W. (2023). Effect of water depth and waterway obstructions on the divergence and confluence areas of Dongting Lake and the Yangtze River after the operation of the Three Gorges Project. River, 2(1), 88–108. https://doi.org/10.1002/rvr2.31
10.1002/rvr2.31
Google Scholar
Yang, Z., Ma, X., Xu, L., Hou, S., Ren, D., & Feng, Q. (2024). A new analytical solution on the frost heaving force of circular tunnel in cold regions. Rock Mechanics and Rock Engineering, 57(5), 3483–3508. https://doi.org/10.1007/s00603-023-03744-y
10.1007/s00603-023-03744-y
Google Scholar
Yang, Z., Xu, J., Feng, Q., Liu, W., He, P., & Fu, S. (2022). Elastoplastic analytical solution for the stress and deformation of the surrounding rock in cold region tunnels considering the influence of the temperature field. International Journal of Geomechanics, 22(8). https://doi.org/10.1061/(ASCE)GM.1943-5622.0002466
10.1061/(ASCE)GM.1943-5622.0002466
Google Scholar
Yu, M., Lin, C. M., Chang, F. Q., & Yin, R. P. (2018). Research on amplification effect of blasting vibration in rock deep foundation pit. Blasting, 34(4), 27–32. https://doi.org/10.3963/j.issn.1001-487X.2017.04.006
10.3963/j.issn.1001-487X.2017.04.006
Google Scholar
Yu, Y., Ling, X., Tang, L., Han, X., Geng, L., & Wei, S. (2021). Analytical solution for the soil-lining interaction in cold region deep tunnel considering the delayed installation of the lining. Cold Regions Science and Technology, 189, 103329. https://doi.org/10.1016/j.coldregions.2021.103329
10.1016/j.coldregions.2021.103329
Google Scholar
Zeng, G. S., Wang, H. N., Song, F., & Rodriguez, A. (2024). Time-dependent analytical solutions for tunnels excavated in anisotropic rheological rock masses. Tunnelling and Underground Space Technology incorporating Trenchless Technology Research, 152. https://doi.org/10.1016/j.tust.2024.105890
10.1016/j.tust.2024.105890
Google Scholar
Zhang, C. G., Gao, B. X., Li, T. B., & Shan, Y. P. (2021). An elastic-plastic solution for frost heaving force of cold region tunnels considering transversely isotropic frost heave and displacement release. Rock and Soil Mechanics, 42(11), 2967–2976. https://doi.org/10.16285/j.rsm.2021.0635
10.16285/j.rsm.2021.0635
Google Scholar
Zhang, C. G., Gao, B. X., Shan, Y. P., & Li, Z. H. (2020). Unified plastic solution for stress and displacement of tunnels in cold regions considering transversely isotropic frost heave. Chinese Journal of Geotechnical Engineering, 42(10), 1825–1831. https://doi.org/10.11779/CJGE202010007
10.11779/CJGE202010007
Google Scholar
Zhang, L. J., Mu, Y. H., Tian, Y., Wang, Y. L., Zhu, X. M., Zhang, K., Zheng, B., & Li, L. (2024). Analytical solution and field observation on temperature field of cold regions tunnel with consideration of diurnal variation in air temperature. Journal of Railway Science and Engineering, 21(6), 2406–2416. https://doi.org/10.19713/j.cnki.43-1423/u.T20231364
10.19713/j.cnki.43-1423/u.T20231364
Google Scholar
Zhang, Z., Wu, X., Xiao, E., He, N., Cheng, K., Zhang, G., Zhou, X., Zhao, C., Wang, H., Du, H., & Jiang, X. (2023). Research and practice of key technologies for landslide dam development and utilization—A case in Hongshiyan landslide Dam Water Conservancy Project. River, 2(3), 251–262. https://doi.org/10.1002/rvr2.51
10.1002/rvr2.51
Google Scholar
Zhao, X., Yang, X., Zhang, H., Lai, H., & Wang, X. (2020). An analytical solution for frost heave force by the multifactor of coupled heat and moisture transfer in cold-region tunnels. Cold Regions Science and Technology, 175, 103077. https://doi.org/10.1016/j.coldregions.2020.103077
10.1016/j.coldregions.2020.103077
Google Scholar
Zhao, Y., Zhang, J., Li, L., Hu, T., & Zhao, Y. (2023). Analytical solution for the temperature field of an elliptical tunnel in cold regions. Cold Regions Science and Technology, 208, 103793. https://doi.org/10.1016/j.coldregions.2023.103793
10.1016/j.coldregions.2023.103793
Google Scholar
Zhao, Y. M., & Dai, S. (2023). Challenges of rock drilling and opportunities from bio-boring. Bio-Geotechnics, 1(1), 100009. https://doi.org/10.1016/J.BGTECH.2023.100009
10.1016/J.BGTECH.2023.100009
Google Scholar
Zhu, Y., Li, Y., Hao, Z., Luo, L., Luo, J., & Wang, L. (2021). An analytical solution for the frost heaving force and displacement of a noncircular tunnel. Computers and Geotechnics, 133, 104022. https://doi.org/10.1016/j.compgeo.2021.104022
10.1016/j.compgeo.2021.104022
Web of Science® Google Scholar
Zuo Q. T., Wang Z. Y., Ma J. X. Hot spots and development prospects of modern water governance research in China. Water Resources Development Research, 2024, 24(6), 13–19. https://doi.org/10.13928/j.carolcarroll_nki_WRDR.2024.06.003
10.13928/j.carolcarroll_nki_WRDR.2024.06.003
Google Scholar
Zhu, J. F., Yin, Q., Zhang, J. M., & Jing, H. W. (2022). Deformation evolution and asymmetric support of deep-buried surrounding rock mass with a gently inclined weak interlayer. Journal of Mining And Strata Control Engineering, 4(05), 47–61. https://doi.org/10.13532/j.jmsce.cn10-1638/td.20220803.001
10.13532/j.jmsce.cn10-1638/td.20220803.001
Google Scholar

Volume3, Issue4

November 2024

Pages 416-425

Analytical study on plastic loosening zone of weak surrounding rocks tunnel in high cold areas

Abstract

1 INTRODUCTION

2 TEMPERATURE–STRESS CHARACTERISTICS