This article proposes a novel and systematic methodology for the inverse optimal control (IOC) of a class of input affine nonlinear systems. First, the system is represented in the pseudo-linear state-dependent coefficient (SDC) form so as to facilitate the use of matrix algebraic concepts in the design, while preserving the nonlinear system dynamics. Second, the IOC problem which seeks the solution to the Hamilton–Jacobi–Bellman equation is translated to a diagonal stability (D-stability) problem. Therefore, the general notion of D-stability, which deals with the characterization of a matrix 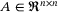for the existence of a diagonal matrix 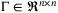such that 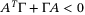, is redefined with respect to SDC factored matrices in this work. Consequently, the criteria for the existence (necessary condition) and determination of a diagonal solution (sufficient condition) are formulated in terms of the SDC matrices. It is shown in this work that these criteria can be readily met by the closed-loop system matrix 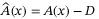, for any arbitrary domain 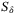in state-space, by manipulating only the diagonal elements using the diagonal matrix 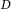constituted by the IOC feedback. In short, the IOC feedback is designed such that the criteria for D-stability by the closed-loop system matrix 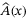is fulfilled. Hence this novel design methodology is meaningfully named as “Inverse optimal control via diagonal stabilization” (IOC-D). The main advantages of IOC-D include: (i) guaranteed estimate of the domain of attraction (DOA), (ii) Immense flexibility of design, and (iii) guaranteed closed form solution which makes the design procedure analytic and computationally efficient. Numerical simulations validate the theoretical developments and the overall efficiency of the proposed approach.