International Journal of Robust and Nonlinear Control

Volume 31, Issue 18 pp. 9709-9730

RESEARCH ARTICLE

A successive convex optimization method for bilinear matrix inequality problems and its application to static output-feedback control

Yingying Ren,

Yingying Ren

Shunde Graduate School of University of Science and Technology Beijing, Guangdong, China

School of Automation and Electrical Engineering, University of Science and Technology Beijing, Beijing, China

Search for more papers by this author

Qing Li,

Qing Li

orcid.org/0000-0002-6361-5008

School of Automation and Electrical Engineering, University of Science and Technology Beijing, Beijing, China

Key Laboratory of Knowledge Automation for Industrial Processes, Ministry of Education, Beijing, China

Search for more papers by this author

Kang-Zhi Liu,

Kang-Zhi Liu

orcid.org/0000-0003-2826-7957

Department of Electrical and Electronic Engineering, Chiba University, Chiba, Japan

Search for more papers by this author

Da-Wei Ding,

Corresponding Author

Da-Wei Ding

[email protected]

orcid.org/0000-0003-1201-7785

School of Automation and Electrical Engineering, University of Science and Technology Beijing, Beijing, China

Key Laboratory of Knowledge Automation for Industrial Processes, Ministry of Education, Beijing, China

Correspondence Da-Wei Ding, School of Automation and Electrical Engineering, University of Science and Technology Beijing, Beijing 100083, China.

Email: [email protected]

Search for more papers by this author

Yingying Ren,

Yingying Ren

Shunde Graduate School of University of Science and Technology Beijing, Guangdong, China

School of Automation and Electrical Engineering, University of Science and Technology Beijing, Beijing, China

Search for more papers by this author

Qing Li,

Qing Li

orcid.org/0000-0002-6361-5008

School of Automation and Electrical Engineering, University of Science and Technology Beijing, Beijing, China

Key Laboratory of Knowledge Automation for Industrial Processes, Ministry of Education, Beijing, China

Search for more papers by this author

Kang-Zhi Liu,

Kang-Zhi Liu

orcid.org/0000-0003-2826-7957

Department of Electrical and Electronic Engineering, Chiba University, Chiba, Japan

Search for more papers by this author

Da-Wei Ding,

Corresponding Author

Da-Wei Ding

[email protected]

orcid.org/0000-0003-1201-7785

School of Automation and Electrical Engineering, University of Science and Technology Beijing, Beijing, China

Key Laboratory of Knowledge Automation for Industrial Processes, Ministry of Education, Beijing, China

Correspondence Da-Wei Ding, School of Automation and Electrical Engineering, University of Science and Technology Beijing, Beijing 100083, China.

Email: [email protected]

Search for more papers by this author

First published: 06 October 2021

https://doi.org/10.1002/rnc.5796

Citations: 2

Funding information: National Natural Science Foundation of China, 61873028; 62103041; Scientific and Technological Innovation Foundation of Shunde Graduate School, USTB, BK19AE021

Share a link

Email
Wechat
Bluesky

Abstract

This article explores a successive convex optimization method for solving a class of nonconvex programming problems subject to bilinear matrix inequality (BMI) constraints. In particular, many control issues can be boiled down to BMI problems, which are typically NP-hard. To get out of the predicament, we propose a more relaxed feasible set to approximate the original one, based on which a local optimization algorithm is developed and its convergence is analyzed. As a case of application, we consider static output-feedback control for uncertain systems with disturbances in restricted frequency intervals. In order to strengthen the disturbance-rejection capability over the given frequency range, we establish sufficient and necessary analysis conditions via the generalized Kalman-Yakubovich-Popov lemma, under which the homogeneous polynomially parameter-dependent technique is adopted to facilitate the design. Finally, several examples are given to demonstrate the efficiency of the results.

CONFLICT OF INTEREST

The authors declare that there are no conflict of interests to this work.

Open Research

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.

REFERENCES

1Dong JX, Yang GH. Static output feedback control synthesis for linear systems with time-invariant parametric uncertainties. IEEE Trans Automat Contr. 2007; 52(10): 1930-1936.
10.1109/TAC.2007.906227
Web of Science® Google Scholar
2Dong JX, Yang GH. Robust static output feedback control synthesis for linear continuous systems with polytopic uncertainties. Automatica. 2013; 49(6): 1821-1829.
10.1016/j.automatica.2013.02.047
Web of Science® Google Scholar
3Scherer C, Gahinet P, Chilali M. Multiobjective output-feedback control via LMI optimization. IEEE Trans Automat Contr. 1997; 42(7): 896-911.
10.1109/9.599969
Web of Science® Google Scholar
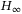4Feng ZY, Xu L, She J, Guo XX. Optimization of coordinate transformation matrix for $urn:x-wiley:10498923:media:rnc5796:rnc5796-math-0394$ static-output-feedback control of linear discrete-time systems. Asian J Control. 2015; 17(2): 604-614.
10.1002/asjc.897
Web of Science® Google Scholar
5Sturm JF. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optim Methods Softw. 1999; 11(1–4): 625-653.
10.1080/10556789908805766
Web of Science® Google Scholar
6Goh KC, Safonov MG, Papavassilopoulos GP. Global optimization for the biaffine matrix inequality problem. J Glob Optim. 1995; 7(4): 365-380.
10.1007/BF01099648
Web of Science® Google Scholar
7Apkarian P, Tuan HD. Robust control via concave minimization local and global algorithms. IEEE Trans Automat Contr. 2000; 45(2): 299-305.
10.1109/9.839953
Web of Science® Google Scholar
8Dinh QT, Gumussoy S, Michiels W, Diehl M. Combining convex–concave decompositions and linearization approaches for solving BMIs, with application to static output feedback. IEEE Trans Automat Contr. 2011; 57(6): 1377-1390.
10.1109/TAC.2011.2176154
Web of Science® Google Scholar
9Wang Y, Rajamani R. Zemouche* a. sequential LMI approach for the design of a BMI-based robust observer state feedback controller with nonlinear uncertainties. Int J Robust Nonlinear Control. 2018; 28(4): 1246-1260.
10.1002/rnc.3948
Web of Science® Google Scholar
10Henrion D, Lofberg J, Kocvara M, Stingl M. Solving polynomial static output feedback problems with PENBMI. Proceedings of the 44th IEEE Conference on Decision and Control. IEEE; 2005: 7581-7586.
10.1109/CDC.2005.1583385
Google Scholar
11Orsi R, Helmke U, Moore JB. A Newton-like method for solving rank constrained linear matrix inequalities. Automatica. 2006; 42(11): 1875-1882.
10.1016/j.automatica.2006.05.026
Web of Science® Google Scholar
12Grigoriadis KM, Skelton RE. Low-order control design for LMI problems using alternating projection methods. Automatica. 1996; 32(8): 1117-1125.
10.1016/0005-1098(96)00057-X
Web of Science® Google Scholar
13El Ghaoui L, Oustry F, AitRami M. A cone complementarity linearization algorithm for static output-feedback and related problems. IEEE Trans Automat Contr. 1997; 42(8): 1171-1176.
10.1109/9.618250
Web of Science® Google Scholar
14Li X, Gao H. Robust frequency-domain constrained feedback design via a two-stage heuristic approach. IEEE Trans Cybern. 2014; 45(10): 2065-2075.
10.1109/TCYB.2014.2364587
PubMed Web of Science® Google Scholar
15Li X, Gao H. Robust finite frequency $urn:x-wiley:10498923:media:rnc5796:rnc5796-math-0395$ filtering for uncertain 2-D Roesser systems. Automatica. 2012; 48(6): 1163-1170.
10.1016/j.automatica.2012.03.012
Web of Science® Google Scholar
16Strunin M, Hiyama T. Response properties of atmospheric turbulence measurement instruments using Russian research aircraft. Hydrol Process. 2004; 18(16): 3099-3117.
10.1002/hyp.5751
Web of Science® Google Scholar
17Xue S, Yang X, Li Z, Gao H. An approach to fault detection for multirate sampled-data systems with frequency specifications. IEEE Trans Syst Man Cybern Syst. 2017; 48(7): 1155-1165.
10.1109/TSMC.2016.2645797
Web of Science® Google Scholar
18Iwasaki T, Hara S. Feedback control synthesis of multiple frequency domain specifications via generalized KYP lemma. Int J Robust Nonlinear Control. 2007; 17(5–6): 415-434.
10.1002/rnc.1123
Web of Science® Google Scholar
19Ding DW, Li XJ, Du X, Xie X. Finite-frequency model reduction of Takagi-Sugeno fuzzy systems. IEEE Trans Fuzzy Syst. 2016; 24(6): 1464-1474.
10.1109/TFUZZ.2016.2540060
Web of Science® Google Scholar
20Petersen IR, McFarlane DC. Optimal guaranteed cost control and filtering for uncertain linear systems. IEEE Trans Automat Contr. 1994; 39(9): 1971-1977.
10.1109/9.317138
Web of Science® Google Scholar
21Geromel JC, Korogui RH. Analysis and synthesis of robust control systems using linear parameter dependent Lyapunov functions. IEEE Trans Automat Contr. 2006; 51(12): 1984-1989.
10.1109/TAC.2006.884958
Web of Science® Google Scholar
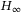22Chang XH, Park JH, Zhou J. Robust static output feedback $urn:x-wiley:10498923:media:rnc5796:rnc5796-math-0396$ control design for linear systems with polytopic uncertainties. Syst Control Lett. 2015; 85: 23-32.
10.1016/j.sysconle.2015.08.007
Web of Science® Google Scholar
23Oliveira RC, Peres PL. Parameter-dependent LMIs in robust analysis: characterization of homogeneous polynomially parameter-dependent solutions via LMI relaxations. IEEE Trans Automat Contr. 2007; 52(7): 1334-1340.
10.1109/TAC.2007.900848
Web of Science® Google Scholar
24Xie X, Yue D, Zhang H, Xue Y. Fault estimation observer design for discrete-time Takagi-Sugeno fuzzy systems based on homogenous polynomially parameter-dependent Lyapunov functions. IEEE Trans Cybern. 2017; 47(9): 2504-2513.
10.1109/TCYB.2017.2693323
PubMed Web of Science® Google Scholar
25Shapiro A. First and second order analysis of nonlinear semidefinite programs. Math Program. 1997; 77(1): 301-320.
10.1007/BF02614439
Web of Science® Google Scholar
26Lee D, Hu J. Sequential parametric convex approximation algorithm for bilinear matrix inequality problem. Optim Lett. 2019; 13(4): 741-759.
10.1007/s11590-018-1274-6
Web of Science® Google Scholar
27Warner E, Scruggs J. Iterative convex overbounding algorithms for BMI optimization problems. IFAC-PapersOnLine. 2017; 50(1): 10449-10455.
10.1016/j.ifacol.2017.08.1974
Google Scholar
28Sebe N. Sequential convex overbounding approximation method for bilinear matrix inequality problems. IFAC-PapersOnLine. 2018; 51(25): 102-109.
10.1016/j.ifacol.2018.11.089
Google Scholar
29Sriperumbudur BK, Lanckriet GR. On the convergence of the concave-convex procedure. Proceedings of the 22nd International Conference on Neural Information Processing Systems. Curran Associates Inc; 2009: 1759-1767.
Google Scholar
30Ishihara JY, Kussaba HTM, Borges RA. Existence of continuous or constant Finsler's variables for parameter-dependent systems. IEEE Trans Automat Contr. 2017; 62(8): 4187-4193.
10.1109/TAC.2017.2682221
Web of Science® Google Scholar
31Iwasaki T, Hara S. Generalized KYP lemma: unified frequency domain inequalities with design applications. IEEE Trans Automat Contr. 2005; 50(1): 41-59.
10.1109/TAC.2004.840475
Web of Science® Google Scholar
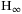32He Y, Wu M, She JH. Improved bounded-real-lemma representation and $urn:x-wiley:10498923:media:rnc5796:rnc5796-math-0397$ control of systems with polytopic uncertainties. IEEE Trans Circuits Syst II Express Briefs. 2005; 52(7): 380-383.
10.1109/TCSII.2005.850418
Web of Science® Google Scholar
33Leibfritz F COMPl $urn:x-wiley:10498923:media:rnc5796:rnc5796-math-0398$ ib: constraint matrix-optimization problem library-a collection of test examples for nonlinear semidefinite programs control system design and related problems; 2004; Department of Mathematics, University of Trier, Trier, Germany.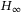
Google Scholar
34Lofberg J. YALMIP: a toolbox for modeling and optimization in MATLAB. Proceedings of the IEEE International Conference on Robotics and Automation. IEEE; 2004: 284-289.
10.1109/CACSD.2004.1393890
Google Scholar
35Sun W, Gao H, Kaynak O. Finite frequency $urn:x-wiley:10498923:media:rnc5796:rnc5796-math-0399$ control for vehicle active suspension systems. IEEE Trans Control Syst Technol. 2010; 19(2): 416-422.
10.1109/TCST.2010.2042296
Web of Science® Google Scholar