In this paper, we study the problem of constructing flat inputs for multi-output dynamical systems, in particular, we address the issue of the minimal modification of the initial dynamical system (the measure of modification being the number of equations that have to be changed by adding flat inputs). We show that in the observable case, control vector fields that distort m equations only (where m is the number of measurements) can always be constructed (and this is the minimal possible number of equations that have to be modified by adding flat inputs), while in the unobservable case, the best that we can hope for is that 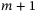equations only are modified such that they involve flat inputs. We discuss when the original output is a flat output of minimal possible differential weight for the minimally modified control system (where by the differential weight, we mean the minimal number of derivatives of components of a flat output needed to express all states and controls). We propose a solution for constructing flat inputs leading to a minimally modified control system consistent with the minimal differential weight and, moreover, for which the observable part is affected by the minimal possible number of controls (this last property being important in applications). We show that, in that case, at least 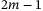equations have to be affected by the flat inputs.