Multiple event-triggered schemes for a class of switched descriptor systems with asynchronous switching
Jiasheng Shi
State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang, China
Key Laboratory of Data Analytics and Optimization for Smart Industry (Northeastern University), Ministry of Education, Shenyang, China
Search for more papers by this authorCorresponding Author
Jun Zhao
State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang, China
College of Information Science and Engineering, Northeastern University, Shenyang, China
Correspondence Jun Zhao, State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang 110819, China; or College of Information Science and Engineering, Northeastern University, Shenyang, 110819, China
Email: [email protected]
Search for more papers by this authorJiasheng Shi
State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang, China
Key Laboratory of Data Analytics and Optimization for Smart Industry (Northeastern University), Ministry of Education, Shenyang, China
Search for more papers by this authorCorresponding Author
Jun Zhao
State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang, China
College of Information Science and Engineering, Northeastern University, Shenyang, China
Correspondence Jun Zhao, State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang 110819, China; or College of Information Science and Engineering, Northeastern University, Shenyang, 110819, China
Email: [email protected]
Search for more papers by this authorFunding information: National Natural Science Foundation of China, 61773098; 61973060; 111 Project, B16009
Abstract
This article studies asynchronous switching for a class of switched descriptor systems (SDSs) under multiple event-triggered schemes (ETSs). First, by using a mode-dependent coordinates transformation, a SDS is equivalently transformed into a reduced-order ordinary switched linear system with state jumps. Then, multiple ETSs are used to transmit the state and switching signal information. The asynchronism between system modes and controller modes inevitably happens in a switching interval. Next, by constructing a controller-mode-dependent Lyapunov functional and using the asynchronous switching strategy, an exponential stability criterion is presented for the closed-loop system with average dwell time switching signals. Meanwhile, the state feedback controller and multiple ETSs are codesigned. Besides, the Zeno behavior is avoided. In the end, the validity of the proposed method is demonstrated by a numerical example.
CONFLICT OF INTEREST
The authors declare no potential conflict of interests.
REFERENCES
- 1
Liberzon D. Switching in Systems and Control. Birkhäuser; 2003.
10.1007/978-1-4612-0017-8 Google Scholar
- 2Long L, Si T. Small-gain technique-based adaptive NN control for switched pure-feedback nonlinear systems. IEEE Trans Cybern. 2019; 49(5): 1873-1884.
- 3Zong G, Ren H, Karimi HR. Event-triggered communication and annular finite-time
filtering for networked switched systems. IEEE Trans Cybern. 2021; 51(1): 309-317.
- 4Shi Y, Zhao J, Liu Y. Switching control for aero-engines based on switched equilibrium manifold expansion model. IEEE Trans Ind Electron. 2017; 64(4): 3156-3165.
- 5 Zong G, Qi W, Karimi HR. L1 control of positive semi-Markov jump systems with state delay. IEEE Trans Syst Man Cybern Syst. 2020. https://doi.org/10.1109/TSMC.2020.2980034
- 6Lin H, Antsaklis PJ. Stability and stabilizability of switched linear systems: a survey of recent results. IEEE Trans Automat Contr. 2009; 54(4): 308-322.
- 7Zhao X, Zhang L, Shi P, Liu M. Stability and stabilization of switched linear systems with mode-dependent average dwell time. IEEE Trans Automat Contr. 2012; 57(7): 1809-1815.
- 8Zhao Y, Liu Y, Ma D. Output regulation for switched systems with multiple disturbances. IEEE Trans Circuits Syst I Regul Pap. 2020; 67(12): 5326-5335.
- 9Liu B, Hill DJ, Sun Z. Input-to-state-KL-stability with criteria for a class of hybrid dynamical systems. Appl Math Comput. 2018; 326: 124-140.
- 10Lu L, Lin Z, Fang H. L2 gain analysis for a class of switched systems. Automatica. 2009; 45: 965-972.
- 11Zhao Y, Yu S, Lian J. Anti-disturbance bumpless transfer control for switched systems with its application to switched circuit model. IEEE Trans Circuits Syst II Express Briefs. 2020; 67(12): 3177-3181.
- 12
Yang D, Zong G, Nguang SK, Zhao X. Bumpless transfer
anti-disturbance control of switching Markovian LPV systems under the hybrid switching. IEEE Trans Cybern. 2020. https://doi.org/10.1109/TCYB.2020.3024988
10.1109/TCYB.2020.3024988 Google Scholar - 13Zong G, Li Y, Sun H. Composite anti-disturbance resilient control for Markovian jump nonlinear systems with general uncertain transition rate. Sci China Inf Sci. 2019; 62(2): 22205.
- 14Park J, Park P. A stability criterion for asynchronously switched linear systems via sampled-data control. Int J Robust Nonlinear Control. 2019; 29(8): 2315-2332.
- 15Li J, Zhang Q. A linear switching function approach to sliding mode control and observation of descriptor systems. Automatica. 2018; 95: 112-121.
- 16
Xu S, Lam J. Robust Control and Filtering of Singular Systems. Springer-Verlag; 2006.
10.1007/11375753_4 Google Scholar
- 17
Duan G. Analysis and Design of Descriptor Linear Systems. Springer-Verlag; 2010.
10.1007/978-1-4419-6397-0 Google Scholar
- 18Liberzon D, Stephan T. On stability of linear switched differential algebraic equations. Proceedings of the IEEE Conference on Decision and Control; 2009:2156-2161.
- 19Zhou L, Ho DW, Zhai G. Stability analysis of switched linear singular systems. Automatica. 2013; 49: 1481-1487.
- 20Zamani I, Shafiee M. On the stability issues of switched singular time-delay systems with slow switching based on average dwell-time. Int J Robust Nonlinear Control. 2014; 24(4): 595-624.
- 21Sun Y, Ma S. Observer-based asynchronous
control for a class of discrete time nonlinear switched singular systems. J Frankl Inst. 2020; 357: 5277-5301.
- 22Yin S, Gao H, Qiu J, Kaynak O. Descriptor reduced-order sliding mode observers design for switched systems with sensor and actuator faults. Automatica. 2017; 76: 282-292.
- 23Zhang J, Zhao X, Zhu F, Karimi HR. Reduced-order observer design for switched descriptor systems with unknown inputs. IEEE Trans Automat Contr. 2019; 65(1): 287-294.
- 24Sajja S, Corless M, Zeheb E, Shorten R. Some stability tests for switched descriptor systems. Automatica. 2019; 106: 257-265.
- 25Mu X, Hu Z. Stability analysis for semi-Markovian switched singular stochastic systems. Automatica. 2020; 118:109014.
- 26Ren W, Xiong J. Razumikhin stability theorems for a general class of stochastic impulsive switched time-delay systems. Int J Robust Nonlinear Control. 2019; 29(12): 3988-4001.
- 27Hetel L, Fridman E. Robust sampled-data control of switched affine systems. IEEE Trans Automat Contr. 2013; 58(11): 2922-2928.
- 28Liberzon D. Finite data-rate feedback stabilization of switched and hybrid linear systems. Automatica. 2014; 50: 409-420.
- 29Lian J, Li C, Xia B. Sampled-data control of switched linear systems with application to an F-18 aircraft. IEEE Trans Ind Electron. 2017; 64(2): 1332-1340.
- 30Tabuada P. Event-triggered real-time scheduling of stabilizing control tasks. IEEE Trans Automat Contr. 2007; 52(9): 1680-1685.
- 31Yue D, Tian E, Han Q. A delay system method for designing event-triggered controllers of networked control systems. IEEE Trans Automat Contr. 2013; 58(2): 475-481.
- 32Shi P, Wang H, Lim C-C. Network-based event-triggered control for singular systems with quantizations. IEEE Trans Ind Electron. 2016; 63(2): 1230-1238.
- 33Peng C, Li F. A survey on recent advances in event-triggered communication and control. Inf Sci. 2018; 457: 113-125.
- 34Zhang X, Han Q, Zhang B. An overview and deep investigation on sampled-data-based event-triggered control and filtering for networked systems. IEEE Trans Ind Inform. 2017; 13(1): 4-16.
- 35Qi Y, Zeng P, Bao W. Event-triggered and self-triggered
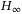control of uncertain switched linear systems. IEEE Trans Syst Man Cybern Syst. 2020; 50(4): 1442-1454.
- 36Li T, Fu J, Deng F, Chai T. Stabilization of switched linear neutral systems: an event-triggered sampling control scheme. IEEE Trans Automat Contr. 2018; 63(10): 3537-3544.
- 37Xiang W, Johnson TT. Event-triggered control for continuous-time switched linear systems. IET Control Theory Appl. 2017; 11(11): 1694-1703.
- 38Ren H, Zong G, Karimi HR. Asynchronous finite-time filtering of networked switched systems and its application: an event-driven method. IEEE Trans Circuits Syst I Regul Pap. 2019; 66(1): 391-402.
- 39Wang Y, Jia Z, Zuo Z. Dynamic event-triggered and self-triggered output feedback control of networked switched linear systems. Neurocomputing. 2018; 314: 39-47.
- 40Liu Y, Zhi H, Wei J, Zhu X, Zhu Q. Event-triggered control for linear continous switched singular systems. Appl Math Comput. 2020; 374:125038.
- 41Xiao X, Zhou L, Ho DW, Lu G. Event-triggered control of continuous-time switched linear systems. IEEE Trans Automat Contr. 2019; 64(4): 1710-1717.
- 42Fei Z, Guan C, Zhao X. Event-triggered dynamic output feedback control for switched systems with frequent asynchronism. IEEE Trans Automat Contr. 2020; 65(7): 3120-3127.
