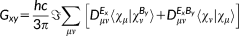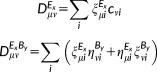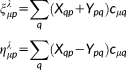Integrated QM/polarizable MM/continuum approaches to model chiroptical properties of strongly interacting solute–solvent systems
Funding Information: Support from the Italian MIUR PRIN 2012 NB3KLK002 and COST CMST-Action CM1405 Molecules in Motion (MOLIM) is acknowledged.
Abstract
Solvent effects on chiroptical properties and spectroscopies can be huge, and affect not only the absolute value but the sign of molecular chiroptical responses. Therefore, the definition of reliable theoretical models and computational protocols to calculate chiroptical responses and assist the assignment of the chiral absolute configuration cannot overlook the effects of the surrounding environment. Continuum solvation methodologies are successful in case of weakly interacting solute–solvent couples, whereas in case of strongly interacting systems, such as those dominated by explicit hydrogen bonding interaction, a change of strategy is required to gain a reliable modeling. In this review, a recently developed integrated Quantum-Mechanical/Polarizable molecular mechanics (MM)/polarizable continuum model (PCM) method is discussed, which combines a fluctuating charge approach to the MM polarization with the PCM. Its theoretical fundamentals, and issues related to the calculation of chiroptical responses are summarized, and the application to few representative test cases in aqueous solution is discussed.
1 Introduction
The calculation of chiroptical properties and chiral spectra by means of Quantum-Mechanical (QM) methods1-5 is a mature research field. Many theoretical developments have been reported in the literature, focusing on the different aspects (accuracy in the description of the molecular Hamiltonian, choice of the basis set, inclusion of environmental effects)3, 6-9 which may contribute to reach an accurate description of chirality. The definition of accurate protocols is nowadays accompanied by several applications, which demonstrate that a significant level of accuracy is accessible, so that QM calculations are universally accepted as a powerful methodology to assist the determination of the molecular absolute configuration.10
In case of standard (non-chiral) spectroscopies, the most relevant information which is extracted from spectra is mainly related to peak positions (energies), whereas peak intensities play a secondary role. This is reflected in the computational methodologies which have been developed so far, which are mainly interested in getting an accurate reproduction of peak positions (infrared/Raman wavenumbers, UV-Vis transition energies, NMR chemical shieldings, etc.), reserving instead much less attention to spectral intensities.11-13 In case of chiroptical properties/spectroscopies, an opposite situation occurs, in fact not only the absolute value but also especially the sign of the spectroscopic response is the most relevant information taken from the spectra. This feature makes chiroptical properties among the most challenging for theoretical models, and the difficulties in their accurate modeling are further increased by that fact that they are formally mixed electric-magnetic properties, where the effects of both the fields are to be considered at the same level of accuracy, as none of the two can be considered as prevailing over the other.
A further complication for a reliable modeling arises from the fact that chiroptical properties and spectroscopies are only seldom measured for isolated systems in the gas phase,14, 15 whereas most experiments are performed for solutions or pure liquids. Also, it has been amply demonstrated that the presence of the external environment may affect not only the absolute value but also especially the sign of the chiroptical response.16, 17 Therefore, the use of either the most accurate levels of calculations may be ineffective if not accompanied by reliable methodologies to take into account environmental effects.9, 18, 19
The most effective strategy to be exploited to model environmental effects on chiroptical properties and spectroscopies is strictly connected to the nature of the environment (solvent)-molecule interactions. In fact, solvent effects may originate both from polarization effects and supramolecular clustering patterns, which cannot be neglected whenever strong interactions, such as hydrogen bonding, dominate the solute–solvent interaction. The extent of such effects, however, strongly depends both on the property and on the solute–solvent couple, being of particular relevance in case of aqueous solutions, which have been demonstrated among the most difficult to be accurately modeled.20
Solvation is surely a complex phenomenon, involving interactions and effects of different nature, which are difficult to be modeled by means of a single theory. In many cases, continuum solvation models are efficient and reliable21-24 especially in their refined formulations including nonequilibrium and local field effects.21, 25, 26 However, they may fail, even dramatically, whenever specific solute–solvent interactions (or solute–solute aggregation effects)21 dominate the solute environment interaction, and especially when a chiral imprinting in the solvation shell can occur.27, 28 In these cases, multiscale QM/MM approaches are required, involving accurate electronic methods to evaluate the chiral properties as well as accurate dynamic simulations to reliably describe the solvent fluctuations, which sustain the chiral response in the solvent cage around the chiral solute.
A well-known case of such a behavior is the optical rotation (OR) of methyloxirane in aqueous solution,29-35 which requires an explicit modeling of the solvation shell around the solute to be adequately described.36 On the contrary, continuum solvation methodologies accurately reproduce the same property of the same molecule in different non-protic solvents, spanning a large range of polarity.29 Also, implicit solvation is accurate enough to reproduce the OR and other chiroptical spectroscopies of aqueous solutions of (S)-N-acetylproline amide,22, 29 where explicit solute–solvent interactions are in principle expected. A different situation occurs for nicotine in aqueous solution,37 where the inclusion of specific solvation effects leads to an improvement in calculated Electronic Circular Dichroism (ECD) spectra, though continuum solvation yields qualitatively correct results, as well as reasonable OR values in isopropanol.29
Therefore, the question of what is the best way to model solvent effects on chiroptical properties of systems in strongly interacting media is far from being finally assessed, especially because implicit solvation model, and the polarizable continuum model (PCM) in particular,38 have been tested thoroughly,9, 17, 39, 40 whereas only few attempts have been performed so far by exploiting explicit or combined explicit/implicit models,28, 36, 39, 41-44 that mainly due to the few hybrid QM/classical molecular mechanics (MM) approaches currently able to calculate chiroptical responses.36, 37, 43, 44 In this review, the latter methodologies are discussed, with particular focus on a recently developed fully polarizable QM/MM/PCM approach,36, 45-50 which has shown to be extremely powerful at overtaking the limitations of continuum solvation approaches.
1.1 QM/classical solvation models for chiroptical properties
Continuum solvation models rooted in the PCM constitute the state-of-the-art of the computational approaches to chiroptical properties/spectroscopies of solvated system, and have become an integral part of the toolkit of scientists working in academia as well as industry. Nowadays, the large majority of the calculations performed to support the assignment of the chiral absolute configuration exploit such approaches, coupled to a QM description of the target system. QM/continuum solvation models for chiroptical properties have been recently reviewed: the interested reader can find a comprehensive discussion in recent literature.9, 18 However, as already mentioned in the Introduction, they suffer from serious limitations. Most important, they may fail dramatically to model strongly interacting molecule-environment couples, such as aqueous solutions, which are nonetheless the natural environment of most biomolecules.
Recent studies36, 37, 42, 44 have demonstrated that such a limitation can be successfully overcome by moving to QM/MM/continuum approaches,51, 52 such as the recently developed fully polarizable QM/FQ/PCM method with nonperiodic boundary conditions,45 which includes polarization effects in the classical MM portion by means of fluctuating charges (FQ)53 and resorts to a continuum PCM treatment of the outer solvation shell. In particular in this model the solvated molecular system is decomposed in three layers, in a multiscale fashion (Figure 1). The inner layer, treated at the QM level (density functional theory [DFT] and coupled-cluster-based methods have been exploited so far, however, the model can be extended to other families of Hamiltonians) is limited to the part of the system which is considered to determine a large part of the property under examination, within the general philosophy of focused models. Within the framework of solvation, such an inner core coincides with the solute. The second layer is constituted by the portion of the environment closer to the solute, and is treated at the atomistic MM level in terms of a set of FQs, which adjust to the QM density. In case of solvation studies, this portion is not covalently bonded to the inner core, however, the formulation of the model is general enough to allow for covalently bonded system to be treated in a ONIOM (our Own N-layer Integrated molecular orbital molecular mechanics)-like structure.54, 55 The QM/FQ system has a droplet-like shape (see Figure 1 for a schematic picture), of which the radius can be adjusted to the needs of the property/system under examination. A third layer, treated as a continuum PCM dielectric is used to account for bulk effects and assures the proper nonperiodic boundary conditions. In the study of solvation, the QM/FQ/PCM approach is used in combination with molecular dynamics (MD) simulations: a series of snapshots from the MD is extracted, which constitute the actual model system on which the QM/FQ/PCM calculations of the desired properties are performed and then averaged out to obtain the final results. Actually, the computational cost of the procedure is mainly determined by the cost of the single QM/FQ/PCM calculation, which basically depends on the QM level and the kind of property (first, second, third derivative, etc.) to be calculated, together with the number of representative snapshots necessary to allow the final results to converge to a sensible value.
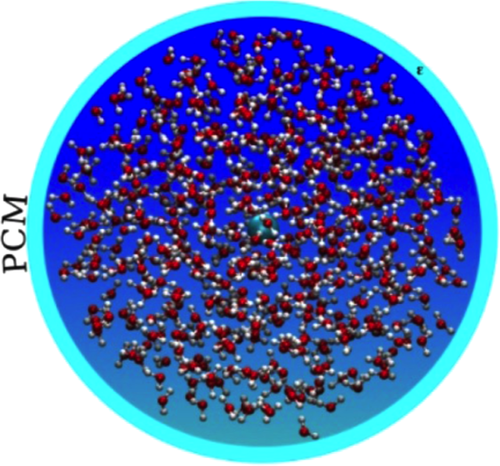
Schematic picture of the QM/FQ/PCM approach
The QM/FQ/PCM approach has recently been extended to treat the evaluation of analytical first and second derivatives,47 response equations,46 magnetic perturbations with gauge including atomic orbitals (GIAOs),48 excitation energies (at the TDDFT46 and EOM-CCSD49 levels of theory), and excitation energy gradients.50 Therefore, most chiroptical responses can be calculated.36, 37, 56 In this section, the physical and computational aspects of this model in connection with the calculation of chiroptical properties are briefly presented, whereas selected examples, showing its potentialities are reported in a forthcoming section.
1.1.1 The QM/FQ/PCM approach
The FQ approach45 is particularly suitable to be employed within a three layer QM/MM/(PCM) framework because of its connection both with quantum mechanics and classical electrostatics. In fact, the model is based on the concepts of atomic hardness and electronegativity, which can be rigorously defined within the DFT,57, 58 and the electronic distribution is represented in terms of a set of classical atomic charges depending on the electrostatic potential. The FQ model, possibly coupled to the PCM can be used to calculate molecular properties by means of response theory or analytical derivatives,46-49 however, it can be also exploited in MD simulations.59 In particular, if the QM/FQ(/PCM) is exploited in a time-independent fashion, the standard machinery of computational chemistry can be employed to calculate structural and spectroscopic properties.37, 46-49
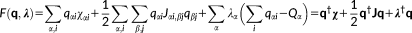 (1)
(1) vector collects the atomic electronegativities, and the J matrix collects the interaction kernel elements between the FQs. In our implementation, the Ohno functional form reference
63 is used:
vector collects the atomic electronegativities, and the J matrix collects the interaction kernel elements between the FQs. In our implementation, the Ohno functional form reference
63 is used:
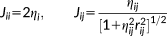 (2)
(2)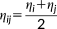
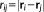 is the distance between two MM atoms. Notice, however, that the implementation is general enough to allow other kernels to be exploited.
is the distance between two MM atoms. Notice, however, that the implementation is general enough to allow other kernels to be exploited.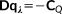 (3)
(3)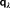 and D includes the J matrix and the Lagrangian blocks.
and D includes the J matrix and the Lagrangian blocks.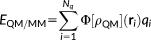 (4)
(4)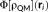 is the electrostatic potential due to the QM density of charge at the ith FQ qi placed at ri.
is the electrostatic potential due to the QM density of charge at the ith FQ qi placed at ri.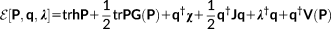 (5)
(5) (6)
(6)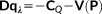 (7)
(7)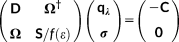 (8)
(8) and with the FQs, respectively, and
and with the FQs, respectively, and
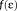 accounts for the dielectric nature of the medium. In addition, a PCM contribution
accounts for the dielectric nature of the medium. In addition, a PCM contribution
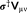 is to be added to
is to be added to
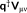 in Equation 6. Further details on the coupling of the PCM with the FQ model can be found elsewhere.45, 46
in Equation 6. Further details on the coupling of the PCM with the FQ model can be found elsewhere.45, 461.1.2 Analytical derivatives and response equations
In the previous section, the physical fundamentals of the QM/FQ/PCM model is given, with the main focus being the definition of the energy. However, the calculation of energies is by definition completely insufficient to address chiroptical phenomena. In fact, to model the chiral response, any theoretical model has to account for the presence of the external polarized radiation. Also, by examining the literature treating the theoretical fundamentals of chirality,64, 65 the reader may be easily convinced that any chiroptical signal arises from the simultaneous interaction of the sample with both the electric and magnetic components of the electromagnetic field. This means that both fields have to be accounted for in the theoretical methodology presented above, and that is generally achieved by resorting to response theory. Also, any computational approach to spectroscopic quantities requires an accurate description of the sample. Among other requirements, this means that a way to determine the minimum energy structure is generally requested, and this is computationally achieved by calculating geometrical energy first (gradients) and second (vibrational frequencies) derivatives. All these quantities have been formulated for the QM/FQ/PCM approach, to enable it to effectively treat chiroptical phenomena. Therefore, this section and the rest of the theoretical part of the article give the technical details of such an extension, up to the formulation of OR and ECD spectra. The reader not interested in the technical details may directly jump to the next part of the article, where some selected examples of application of the method are discussed.
As it was mentioned in the previous paragraph, to discuss the extension of the QM/FQ/PCM method to chiral phenomena, it is worth briefly recalling the extension of the QM/FQ/PCM method to the evaluation of analytical first and second derivatives,47 response equations to electric46 and magnetic perturbations with GIAOs.48 In following treatment, only FQ terms will be considered: extension to PCM does not add any substantial difference, but only makes the notation more cumbersome. The reader interested in the details can find them in references 46 and 47.
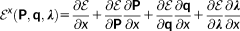 (9)
(9)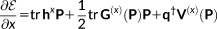 (10)
(10)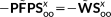
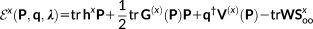 (11)
(11)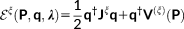 (12)
(12)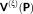 is nothing else than the electric field produced by the QM density acting on the FQs,
is nothing else than the electric field produced by the QM density acting on the FQs,
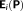 (see reference
47 for more details).
(see reference
47 for more details).Second order response properties can be analytically derived by calculating the second derivatives of the variational QM/FQ energy. According to the philosophy of focused models, the extension of the QM/FQ/PCM approach to second derivatives has been done by assuming the external perturbation (i.e., the electric field or a nuclear displacement) only acting on the QM portion of the system, whereas indirect effects on the MM part through the perturbation on the QM density are considered. This approach cannot be applied when the QM and MM portions are covalently bonded, however, alternative approaches such as the ONIOM54, 55 extrapolation can be applied.
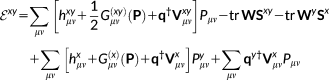 (13)
(13)Equation 13 involves FQ explicit contributions and response contributions, involving density matrix derivatives. The latter are obtained through a set of coupled perturbed Hartree Fock (CPHF) equations including FQ/PCM terms.46, 47 Therefore, electric, magnetic or vibrational properties require the evaluation of the perturbed density matrix and, possibly, of the perturbed FQs (and PCM charges).
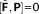 , we obtain the following equation:
, we obtain the following equation:
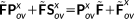 (14)
(14)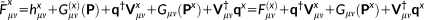 (15)
(15) (16)
(16)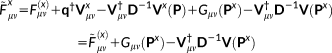 (17)
(17)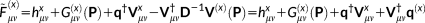
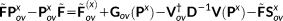 (18)
(18)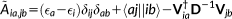 (19)
(19) (20)
(20)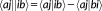 are standard antisymmetrized bielectronic integrals.
are standard antisymmetrized bielectronic integrals.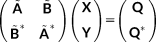 (21)
(21)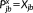 and
and
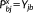 . The solution of Equations 21 and 16 yields the derivatives of the density matrix and the FQs with respect to QM nuclear positions, respectively, thus allowing the calculation of energy second derivatives.
. The solution of Equations 21 and 16 yields the derivatives of the density matrix and the FQs with respect to QM nuclear positions, respectively, thus allowing the calculation of energy second derivatives.The formulas for the full Hessian matrix, that is, including also the QM/MM and MM/MM blocks, can be found in reference 47.
1.1.3 Electric perturbations
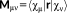 are dipole integrals):
are dipole integrals):
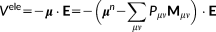 (22)
(22)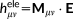 (23)
(23)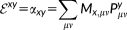 (24)
(24)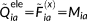 (25)
(25)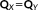 and the equations may be solved for X + Y. By summing up the CPHF equations, we obtain:
and the equations may be solved for X + Y. By summing up the CPHF equations, we obtain:
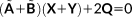 (26)
(26)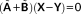 , where
, where
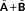 involves an FQ contribution.
involves an FQ contribution.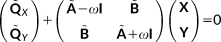 (27)
(27)1.1.4 Magnetic perturbations
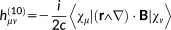 (28)
(28)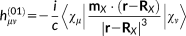 (29)
(29)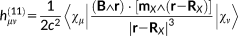 (30)
(30)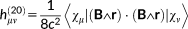 (31)
(31)In the previous equations, the Coulomb Gauge is exploited. h(01) represents the first-order contribution to the interaction between the electronic motion and the external magnetic field; h(10) is the corresponding first-order term which couples the nuclear magnetic moment to the electronic motion; h(20) and h(11) are second order terms connected with the diamagnetic contribution, respectively, to the magnetizability and to the magnetic shielding. Notice that in principle a further h(02) term should be present,69 that is, a second-order term relative to the interaction between the electrons and the nuclear magnetic moment, which is, however, not of interest to the present case.
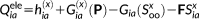 (32)
(32)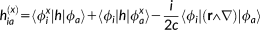 (33)
(33)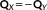 , so that the response equations can be solved for X − Y. By subtracting the response equations
, so that the response equations can be solved for X − Y. By subtracting the response equations
 (34)
(34)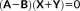 . Notice that in this case A − B does not include any FQ response contribution. The contribution to the right-hand side of the QM/FQ response equation reads
. Notice that in this case A − B does not include any FQ response contribution. The contribution to the right-hand side of the QM/FQ response equation reads
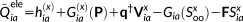 (35)
(35)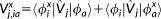
Again, the FQs contribute indirectly to the magnetic response.
1.2 Optical rotation
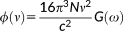
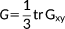
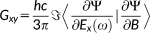 (36)
(36)λ = E, B and the X and Y transition densities are obtained by solving the response equations for the (frequency dependent) electric and magnetic fields, respectively.
1.3 Electronic circular dichroism
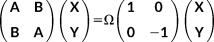 (38)
(38)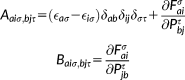 (39)
(39)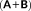 and
and
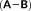 with the (X + Y) and (X − Y) vectors, carried out in the atomic orbital basis.
with the (X + Y) and (X − Y) vectors, carried out in the atomic orbital basis.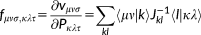 (40)
(40)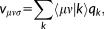 (41)
(41)The FQ contribution is purely electrostatic, and only contributes to the symmetric combination (A + B). Once the Casida equations are solved and excitation energies and transition amplitudes are known, the rotatory strength tensors can be computed in the velocity form, as described in reference 81 The integrals of the electric and magnetic multipoles are computed and stored in AO basis set, and then are traced with the transition densities.
2 Some selected examples
In this section, some illustrative examples are reported, with the aim of showing the potentialities of the QM/FQ/PCM approach. In particular, the first test case concerns a rigid small molecule, methyloxirane in aqueous solution, which has been reported to be particularly challenging for continuum solvent methodologies. The second example refers to a flexible molecule of medium size, nicotine, again in aqueous solution, which has as well been taken as reference for testing the performance of continuum solvation models.18 For each case, the comparison between the QM/FQ/PCM and both experimental data and continuum solvation approaches is proposed, the latter to especially evidence the role of short-range specific interactions with respect to long-range bulk effects.
2.1 The OR of (R)-methyloxirane
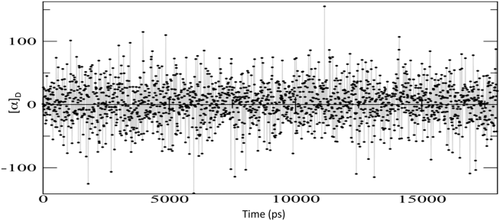
A well-known example of huge solvent effects on chiroptical properties is the OR of methyloxirane in aqueous solution.29, 30, 35, 82, 83 The application of the PCM approach has been amply reported, showing that continuum solvation is a viable tool to describe the OR of methyloxirane whenever solvent effects are dominated by bulk contributions, that is, for weakly interacting solute–solvent couples. Even in this case, however, to obtain reliable results, the basic PCM formulation is not completely adequate, and local field/nonequilibrium effects should be included in the modeling of the electronic property.26, 29 Also, vibrational corrections calculated with the inclusion of anharmonic terms give a substantial contribution to the final computed property, which permit to finally recover the experimental findings. On the contrary, in cases dominated by specific solute–solvent interactions, even this refined model is not able to correctly reproduce solvent effects, which can be large enough to change the sign of the OR value. The reason for such an effect can be understood from the data reported in Figure 2, where the results obtained by calculating with the QM/FQ/PCM approach the OR on 2000 snapshots taken from a MD simulation are given. The set of 2000 representative structures was obtained by cutting, for each snapshot, a sphere centered in the solute's geometrical center of 16 Å. A 1.5 Å larger radius was used to define the PCM spherical cavity representing the third layer (more details on the computational protocol can be found in reference 36). It is in particular worth to notice that the snapshots were extracted from a MD performed by keeping fixed the methyloxirane structure, that is, the snapshots only differ by a different arrangement of the water molecules around methyloxirane. Figure 2 clearly shows a large variability of the OR as a function of the particular geometrical arrangement of water around the target molecule. The OR can vary sensitively, not only in absolute value, but especially in sign, taking any value in the range −150/150 deg dm−1 g−1 cm3. This means that any static approach to such property, such as the PCM or simple cluster-based models, where the specific interaction is modeled by redefining the solute as the target molecule plus a limited number of explicitly treated solvent molecules, will most probably give a result falling in this range, however, a good reproduction of the average value is not guaranteed. This is more clearly explained in Figure 3, which reports the OR calculated values as obtained by using the PCM and the QM/FQ/PCM approach. The experimental value83 is also reported for comparison's sake. The solvent effect modeled by PCM goes in the right direction with respect to the value in vacuo, that is, a decrease in the absolute value is obtained. However, the account of bulk effects only is unable to correctly predict the OR sign, which is instead successfully recovered when the explicit presence of the water around methyloxirane is modeled by means of the QM/FQ/PCM approach. Notably, such an agreement is not limited to a single wavelength (see Figure 4), but the entire ORD curve is well reproduced by the hybrid explicit/implicit QM/FQ/PCM model, also as varying the choice of the density functional.84
Calculated QM/FQ/PCM optical rotation of (s)-methyloxirane at 589 nm as a function of the snapshot extracted form the molecular dynamics simulation. QM level: B3LYP/aug-cc-pVDZ
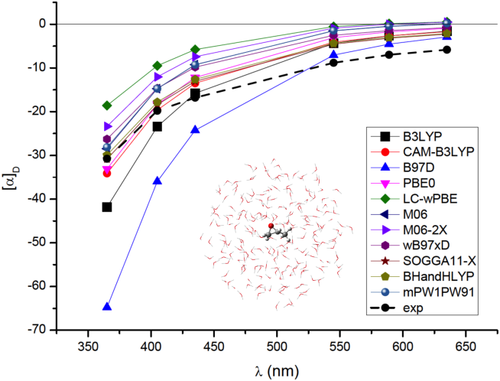
Calculated QM/FQ/PCM optical rotatory dispersion by exploiting the aug-cc-pVDZ basis set and different DFT functionals84
It is also to notice that the analysis of the snapshots of MD simulations did not evidence any dominant solute–solvent configurations, that is, any persistent hydrogen bonding pattern around methyloxirane. This is probably the reason for the slow convergence of the property with respect to the simulation time, and the need of averaging over a huge (2000) number of snaphshots to allow the property to converge to a sensible value. Furthermore, such an absence of predominant patterns explains the failure of computational protocols based on clusters. Such approaches have been applied to this case30, 82 by re-defining the solute molecule in terms of a large number of clusters including only a limited number of solvent molecules, which were then treated at the QM level in the evaluation of the OR. A large effect of specific solute–solvent interactions in determining the sign of the calculated OR was obtained, however, a quantitative agreement with the experimental values was not achieved.
2.2 The ECD of (S)-nicotine
The example which has been reported in the previous section regards a rigid molecule, which has a single prevalent conformation. However, this is not the case of most molecules, which generally have conformational flexibility. As an example of nonrigid chiral molecules, in this section the ECD spectrum of (S)-nicotine is discussed.37, 85
Neutral nicotine (see inset in Figure 5 for its structure) exists in two possible conformations, denoted as A and B, which are defined through a rotation around the
 angle. Calculated populations of the two conformers by exploiting the PCM and the CAM-B3LYP/aug-ccpVDZ/level of theory show a prevalence of the A conformer (55.3% population) over the B one.
angle. Calculated populations of the two conformers by exploiting the PCM and the CAM-B3LYP/aug-ccpVDZ/level of theory show a prevalence of the A conformer (55.3% population) over the B one.
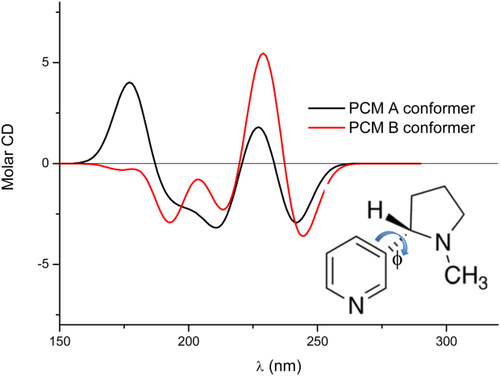
Calculated CAMB3LYP/aug-cc-pVDZ/PCM ECD spectra of the A and B conformers of trans-(S)-nicotine in aqueous solution
The two conformations show a very similar behavior in terms of the oscillator strengths of similar transitions, that is, very similar absorption spectra,37 however, the same is not true for rotatory strengths (R), determining ECD spectra. In fact (see Figure 5), in the region around 175 nm the sign of the rotatory strengths of the two conformers are opposite, with the A conformer showing a positive and large R value, whereas the B conformer has a low, negative value. Around 225 nm the sign of the R of the two conformers is the same, however, the B rotatory strength is generally higher compared with the other conformer. Therefore, despite the B conformation is predicted to be less populated by the PCM, it is expected to dominate the ECD spectrum in that region nonetheless. The final PCM ECD spectrum is therefore the result of the subtle interplay between the conformer populations and their relative R values. The resulting spectrum is shown in Figure 6, where the experimental spectrum37 is also reported for comparison's sake. Clearly, the PCM yields results that qualitatively agree with the experimental values, however, a quantitative reproduction of peak intensities is not achieved. Notice that the variation of the ECD spectrum on conformation (Figure 5) is not surprising. In fact, the close relationship between conformations and sign and magnitude of chiroptical properties has been reported in the literature,86, 87 and has been extensively investigated by Wiberg and coworkers (see reference 87 and references therein).
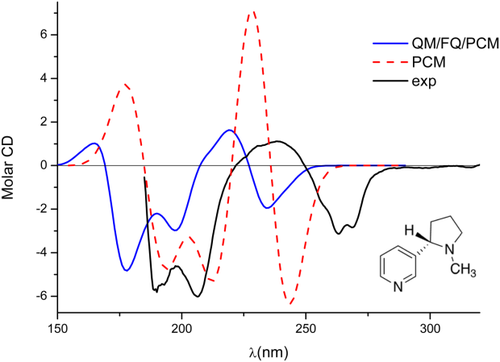
Calculated QM/FQ/PCM and averaged QM/PCM ECD spectra of (S)-nicotine in aqueous solution. In all cases, the CAMB3LYP/aug-cc-pVDZ level is exploited in QM calculations. The experimental spectrum, taken from reference 37 is also reported
Because of its two basic lone pairs, nicotine is expected to undergo hydrogen bonding with water molecules, of which the effects can be evaluated by exploiting a MD simulation followed by QM/FQ/PCM calculations on selected snapshots (more details on the computational protocol can be found in reference 37).
The application of MD simulations to extract data on the conformational preference, shows that by exploiting the general Amber force field88 with atomic charges calculated by applying the multiconformation RESP (MultiRESP)89 procedure and water molecules modeled using the TIP4P/200590 parameter set, the B conformer is found to be the most stable, at variance with QM/PCM findings. The analysis of nitrogen-hydrogen radial distribution functions between nitrogen atoms in nicotine and hydrogen atoms in water molecules indicates the presence of first and second hydration shells separated from the bulk solvent. In particular, the aliphatic nitrogen (see inset in Figure 5) forms a very stable hydrogen bond with one water molecule, whereas the hydration structure of the aromatic nitrogen atom is much less defined compared with that of the aliphatic one. Also, in the case of the A conformer, the aliphatic nitrogen shows well-defined first and second hydration shells, while the aromatic nitrogen hydration structure is less defined. However, when conformer B is considered, the existence of a cooperative effect in which bridging water–water hydrogen bonds stabilize the B conformer, creating less disorder in the water liquid structure, can be found. The results of the MD simulations were also used to extract a set of snapshots to be exploited to compute ECD spectra of nicotine in the QM/FQ/PCM scheme. In particular, each snapshot was centered on the center of mass of the solute, around which a solvation sphere of radius 14 Å, containing an average of 366 water molecules, was cut. A 2.5 Å larger radius was used to define the PCM spherical cavity, used as boundary for the third layer.
The QM/FQ/PCM ECD spectrum was then obtained by averaging out the spectra of the single snapshots. The final result is shown in Figure 6; the sign pattern agrees with experiments, however, the relative intensities of the bands do not perfectly match the experimental spectrum. The discrepancy, however, is much lower than in case of QM/PCM results, thus demonstrating a significant improvement in the results with the inclusion of explicit hydrogen bonding effects, affecting both in TD-DFT calculations and the conformational sampling. It is also to notice that the convergence of the spectrum is achieved by averging 300 snapshots, that is, a number of an order of magnitude less than what is required to allow OR of methyloxirane to converge.
3 Conclusions and perspectives
In this review the modeling of the chiroptical properties of strongly interacting solute–solvent systems is discussed, with particular reference to recently developed integrated fully polarizable QM/FQ/PCM approaches and their formal extension to treat mixed electric-magnetic responses which allow chiroptical responses to be calculated. Surely, solvation is a complex phenomenon, therefore unique and optimal protocols are difficult to be established, so that the selection of the different formulations and combinations of approaches strongly depends on the particular physical phenomenon and on the nature of the molecular system. However, the application of such methods to challenging test cases shows that they are able to accurately describe those systems where the most common continuum solvent methodologies fail, therefore they are very promising for an extensive future application.
Although the formal development of QM/FQ/PCM approaches is mature enough to allow for most chiroptical properties/spectroscopies to be calculated, an extensive and general application would require some further steps. First, it would be necessary to widen the applicability of such approaches to nonaqueous environments, such as benzene solutions, which are dominated by dispersion interactions, and for which the so-called chiral imprint28 has been invoked. To date QM/MM methodologies have been mostly formulated within the so-called electrostatic (polarizable and nonpolarizable) embedding framework, whereas dispersion interactions are accounted for classically. Some steps toward this direction have been done for other families of methods,91-94 and a similar extension of the QM/FQ/PCM approach to treat such interactions would be necessary to enlarge the spectrum of possible applications. Strictly connected to this point is parametrization, which means at the same time a more accurate parametrization for aqueous solutions, able to reproduce the finest spectral features, and the extension to different solvents and different external environments. With regard to this last point, it is to remark that the QM/FQ/PCM approach has been originally formulated to treat solvated systems. However, formally there is not any obstacle to its extension to treat probes in matrices/protein, even in case of covalently bonded systems, provided that a suitable parametrization is achieved and nonelectrostatics is considered. Such an extension would be substantial to model supramolecular chirality,95, 96 as well as enhanced97 and induced98 chirality, which nowadays constitute the most cutting edge fields in the study of chiral systems.
Acknowledgments
Support from the Italian MIUR PRIN 2012 NB3KLK002 and COST CMST-Action CM1405 Molecules in Motion (MOLIM) is acknowledged.
Biography

Chiara Cappelli received a Ph.D. in Chemistry in 2002 from the Scuola Normale Superiore, Pisa, Italy. After four years as postdoctoral fellow at the Italian Institute for the Physics of Matter (INFM-CNR), she joined the faculty at the University of Pisa. From 2015, she is an Associate Professor at the Scuola Normale Superiore in Pisa. Her research activity focuses on the development of theoretical models and computational codes to treat solvent effects on molecular properties and spectroscopies.