Original Article
Lognormal Distributions and Geometric Averages of Symmetric Positive Definite Matrices
Armin Schwartzman,
Armin Schwartzman
Department of Statistics, North Carolina State University, Raleigh, NC, USA
Search for more papers by this authorArmin Schwartzman,
Armin Schwartzman
Department of Statistics, North Carolina State University, Raleigh, NC, USA
Search for more papers by this authorSummary
This article gives a formal definition of a lognormal family of probability distributions on the set of symmetric positive definite (SPD) matrices, seen as a matrix-variate extension of the univariate lognormal family of distributions. Two forms of this distribution are obtained as the large sample limiting distribution via the central limit theorem of two types of geometric averages of i.i.d. SPD matrices: the log-Euclidean average and the canonical geometric average. These averages correspond to two different geometries imposed on the set of SPD matrices. The limiting distributions of these averages are used to provide large-sample confidence regions and two-sample tests for the corresponding population means. The methods are illustrated on a voxelwise analysis of diffusion tensor imaging data, permitting a comparison between the various average types from the point of view of their sampling variability.
References
- Alexander A. L., Hasan K., Kindlmann G., Parker D. L., Tsuruda J. S.. 2000. A geometric analysis of diffusion tensor measurements of the human brain. Magn. Reson. Med. 44(2): 283–291.
- Anderson T. W.. 2003. An Introduction to Multivariate Statistical Analysis, 3. John Wiley & Sons Ltd.: Hoboken, New Jersey.
- Arsigny V., Fillard P., Pennec X., Ayache N.. 2006. Log-Euclidean metrics for fast and simple calculus on diffusion tensors. Magn. Reson. Med. 56(2): 411–421.
- Arsigny V., Fillard P., Pennec X., Ayache N.. 2007. Geometric means in a novel space structure of symmetric positive definite matrices. SIAM J. Matrix. Anal. Appl. 29(1): 328–347.
- Ashburner J., Friston K. J.. 1999. Nonlinear spatial normalization using basis functions. Hum. Brain Map. 7: 254–266.
- Bammer R., Auer M., Keeling S. L., Agustin M., Stables L. A., Prokesch R. W., Stollberger R., Moseley M. E., Fazekas F.. 2002. Diffusion tensor imaging using single-shot SENSE-EPI. Magn. Reson. Med. 48: 128–136.
- Basser P. J., Pierpaoli C.. 1996. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J. Magn. Reson. B 111: 209–219.
- Batchelor P. G., Moakher M., Atkinson D., Calamante F., Connelly A.. 2005. A rigorous framework for diffusion tensor calculus. Magn. Reson. Med. 53: 221–225.
- Benjamini Y., Hochberg Y.. 1995. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Statist. Soc. B 57(1): 289–300.
10.1111/j.2517-6161.1995.tb02031.x Google Scholar
- Bhatia R.. 2007. Positive Definite Matrices.Princeton University Press: Woodstock, Oxfordshire, England.
- Bhatia R., Holbrook J.. 2006. Riemannian geometry and matrix geometric means.Linear Algebra Appl. 413: 594–618.
- Bhattacharya A., Bhattacharya R. N.. 2008. Statistics on Riemannian manifolds: asymptotic distribution and curvature. Proc. Am. Math. Soc. 33(3): 1225–1259.
- Bhattacharya R. N., Elligson L., Liu X., Patrangenaru V., Crane M.. 2012. Extrinsic analysis on manifolds is computationally faster than intrinsic analysis, with applications to quality control by machine vision. Appl. Stochastic Models Bus. Ind. 28: 222–235.
- Bhattacharya R. N., Patrangenaru V.. 2003. Large sample theory of intrinsic and extrinsic sample means on manifolds. I. Ann. Statist. 31(1): 1–29.
- Bhattacharya R. N., Patrangenaru V.. 2005. Large sample theory of intrinsic and extrinsic sample means on manifolds. II. Ann. Statist. 33(3): 1225–1259.
- Calvo M., Oller J. M.. 1991. An explicit solution of information geodesic equations for the multivariate normal model. Stat. Decis. 9: 119–138.
- Chiu T. Y. M., Leonard T., Tsui K. W.. 1996. The matrix-logarithmic covariance model. J. Amer. Statist. Assoc. 91(433): 198–210.
- DoCarmo M. P.. 1992. Riemannian Geometry.Birkhauser: Boston.
- Dougherty R. F., Ben-Shachar M., Deutsch G. K., Hernandez A., Fox G. R., Wandell B. A.. 2007. Temporal-callosal pathway diffusivity predicts phonological skills in children. PNAS 104(20): 8556–8561.
- Dougherty R. F., Ben-Shachar M., Deutsch G. K., Potanina P., Wandell B. A.. 2005. Occipital–callosal pathways in children: validation and atlas development. Ann. N. Y. Acad. Sci. 1064: 98–112.
- Dryden I. L., Koloydenko A., Zhou D.. 2009. Non-Euclidean statistics for covariance matrices, with applicationns to diffusion tensor imaging. Ann. of Appl. Statist. 3(3): 1102–1123.
- Ellingson L., Groisser D., Osborne D., Patrangenaru V., Schwartzman A.. 2012. Nonparametric bootstrap of sample means of positive definite matrices with an application to diffusion tensor imaging data analysis. In Technical Report M1005 http://www.stat.fsu.edu/techreports.php.
- Fillard P., Pennec X., Arsigny V., Ayache N.. 2007. Clinical DT-MRI estimation, smoothing, and fiber tracking with log-Euclidean metrics. IEEE-T. Med. Imaging 26(11): 1472–1482.
- Fletcher P. T., Joshi S.. 2007. Riemannian geometry for the statistical analysis of diffusion tensor data. Signal Process. 87(2): 250–262.
- Forstner W., Moonen B.. 1999. A metric for covariance matrices. In Quo Vadis Geodesia...?, Festschrift for Erik W. Grafarend on the Occasion of his 60th Birthday, S. Volker, F. K. Schwarze (eds), number 1999.6 in Technical Reports Department of Geodesy and Geoinformatics; 113–128. Stuttgart University.
- Fréchet M.. 1948. Les éléments aléatoires de nature quelconque dans un espace distancié. Ann. Inst. H. Poincaré 10: 215–310.
- Goldberg K.. 1956. The formal power series for log(exey). Duke Math. J. 23: 13–21.
- Groisser D.. 2004. Newton's method, zeroes of vector fields, and the Riemannian center of mass. Adv. Appl. Math. 33: 95–135.
- Gupta A. K., Nagar D. K.. 2000. Matrix Variate Distributions. Boca Raton, Florida: Chapman & Hall/CRC.
- Henderson H. V., Searle S. R.. 1979. Vec and vech operators for matrices, with some uses in Jacobians and multivariate statistics. Can. J. Stat. 7: 65–81.
10.2307/3315017 Google Scholar
- Johnson N. L., Kotz S.. 1970. Continuous Univariate Distributions-1.John Wiley & Sons: New York.
- Joshi A. A., Shattuck D. W., Thompson P. M., Leahy R. M.. 2007. Surface-constrained volumetric brain registration using harmonic mappings. IEEE-T. Med. Imaging 26(12): 1657–1669.
- Kobayashi S., Nomizu K.. 1996. Fundamentals of Differential Geometry–Volume II.John Wiley & Sons Inc.: New York.
- Lang S.. 1999. Fundamentals of Differential Geometry.Springer-Verlag: New York.
- Lawson J. D., Lim Y.. 2001. The geometric mean, matrices, metrics, and more. Am. Math. Mon. 108(9): 797–812.
- Lawson J. D., Lim Y.. 2013. Weighted means and Karcher equations of positive operators. PNAS 110(39): 15626–15632.
- LeBihan D., Mangin J. -F., Poupon C., Clark C. A., Pappata S., Molko N., Chabriat H.. 2001. Diffusion tensor imaging: concepts and applications. J. Magn. Reson. Imaging 13: 534–546.
- Lenglet C., Rousson M., Deriche R., Faugeras O.. 2006. Statistics on the manifold of multivariate normal distributions: theory and application to diffusion tensor MRI processing. J. of Math. Imaging and Vision 25(3): 423–444.
- Leonard T., Hsu J. S. J.. 1992. Bayesian inference for a covariance matrix. Ann. Statist. 20(4): 1669–1696.
- Leporé N., Brun C., Chou Y. -Y., Chiang M. -C., Dutton R. A., Hayashi K. M., Lueders E., Lopez O. L., Aizenstein H. J., Toga A. W., Becker J. T., Thompson P. M.. 2008. Generalized tensor-based morphometry of HIV/AIDS using multivariate statistics on deformation tensors. IEEE-T. Med. Imaging 27(1): 129–141.
- Magnus J. R., Neudecker H.. 1980. The elimination matrix: some lemmas and applications. SIAM J. Algebra Discr. Meth. 1: 422–449.
- Mardia K. V., Kent J. T., Bibby J. M.. 1979. Multivariate Analysis.Academic Press: San Diego, California.
- Mehrabadi M. M., Cowin S. C., Jaric J.. 1995. Six-dimensional orthogonal tensor representation of the rotation about an axis in three dimensions. Int. J. Solids Struct. 32(3/4): 439–449.
- Mehta M. L.. 1991. Random Matrices, 2. Academic Press: San Diego, California.
- Moakher M.. 2005. A differential geometric approach to the geometric mean of symmetric positive-definite matrices. SIAM Matrix Anal. Appl. 26(3): 735–747.
- Moakher M., Batchelor P. G.. 2006. Symmetric positive-definite matrices: from geometry to applications and visualization. In Visualization and Processing of Tensor Fields, Ch. 17, pp. 285–298.Springer.
- Moakher M., Zéraï M. 2011. The Riemannian geometry of the space of positive-definite matrices and its application to the regularization of positive-definite matrix-valued data. J. Math. Imaging Vis. 40: 171–187.
- Muirhead R. J.. 1982. Aspects of Multivariate Statistical Theory.John Wiley & Sons Ltd.: Hoboken, New Jersey.
10.1002/9780470316559 Google Scholar
- Newman M., Thompson R. C.. 1987. Numerical values of Goldberg's coefficients in the series for log(exey). Math. Comput. 48(177): 265–271.
- Oller J. M., Corcuera J. M.. 1995. Intrinsic analysis of statistical estimation. Ann. Statist. 23(5): 1562–1581.
- Osborne D., Patrangenaru V., Ellingson L., Groisser D., Schwartzman A.. 2013. Nonparametric two-sample tests on homogeneous Riemannian manifolds, Cholesky decompositions and diffusion tensor image analysis. J. Multivariate Anal. 119: 163–175.
- Pasternak O., Sochen N., Basser P. J.. 2010. The effect of metric selection on the analysis of diffusion tensor MRI data. Neuroimage 49(3): 2190–2204.
- Pennec X., Fillard P., Ayache N.. 2006. A Riemannian framework for tensor computing. Int. J. Comput. Vision 66(1): 41–66.
- Pennec X.. 2006. Intrinsic statistics on Riemannian manifolds: basic tools for geometric measurements. J. Math. Imaging Vis. 25: 127–154.
- Schott J. R.. 2005. Matrix Analysis for Statistics, 2. John Wiley & Sons Ltd.: Hoboken, New Jersey.
- Schwartzman A.. 2006. Random ellipsoids and false discovery rates: statistics for diffusion tensor imaging data. PhD thesis, Stanford University.
- Schwartzman A., Dougherty R. F., Taylor J. E.. 2010. Group comparison of eigenvalues and eigenvectors of diffusion tensors. J. Amer. Statist. Assoc. 105(490): 588–599.
- Schwartzman A., Mascarenhas W., Taylor J. E.. 2008. Inference for eigenvalues and eigenvectors of Gaussian symmetric matrices. Ann. Statist. 36(6): 2886–2919.
- Shurbet G. L., Lewis T. O., Boullion T. L.. 1974. Quadratic matrix equations. Ohio J. Sci. 74(5): 273–277.
- Skovgaard L. T.. 1984. A Riemannian geometry of the multivariate normal model. Scand. J. Stat. 11(4): 211–223.
- Smith S.. 2005. Covariance, subspace, and intrinsic Cramér–Rao bounds. IEEE Trans. Signal Process. 53(5): 1610–1630.
- Terras A.. 1987. Asymptotics of special functions and the central limit theorem on the space
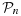of positive n × n matrices. J. Multivariate Anal. 23: 13–36.
- Whitcher B., Wisco J. J., Hadjikhani N., Tuch D. S.. 2007. Statistical group comparison of diffusion tensors via multivariate hypothesis testing. Magn. Reson. Med. 57: 1065–1074.
- Yao Y.. 1965. An approximate degrees of freedom solution to the multivariate Behrens–Fisher problem. Biometrika 52: 139–147.
- Zhu H., Chen Y., Ibrahim J. G., Li Y., Hall C., Lin W.. 2009. Intrinsic regression models for positive-definite matrices with applications to diffusion tensor imaging. J. Amer. Statist. Assoc. 104(487): 1203–1212.
