RESEARCH ARTICLE
control of stochastic networked control systems with time-varying delays: The event-triggered sampling case
Quanxin Zhu,
Tingwen Huang,
Corresponding Author
Quanxin Zhu
MOE-LCSM, School of Mathematics and Statistics, Hunan Normal University, Changsha, China
Correspondence Quanxin Zhu, MOE-LCSM, School of Mathematics and Statistics, Hunan Normal University, Changsha, Hunan 410081, China.
Email: [email protected]
Search for more papers by this authorTingwen Huang
Science Program, Texas A & M University at Qatar, Doha, Qatar
Search for more papers by this authorQuanxin Zhu,
Tingwen Huang,
Corresponding Author
Quanxin Zhu
MOE-LCSM, School of Mathematics and Statistics, Hunan Normal University, Changsha, China
Correspondence Quanxin Zhu, MOE-LCSM, School of Mathematics and Statistics, Hunan Normal University, Changsha, Hunan 410081, China.
Email: [email protected]
Search for more papers by this authorTingwen Huang
Science Program, Texas A & M University at Qatar, Doha, Qatar
Search for more papers by this authorFunding information: the National Natural Science Foundation of China, 62173139
Abstract
In this article, we aim to study the robust stabilization problem for a class of stochastic networked control delay systems with time-varying delays and unknown parameters. By developing an event-triggered strategy, the robustly exponential stability in mean-square of the suggested system with an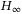 
performance is obtained. Furthermore, the robustly exponential stabilization problem in mean-square is also solved by designing an 
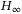controller. Compared with many published results in the literature for discrete-time stochastic systems, our work mainly focuses on the case of continuous-time stochastic systems. In particular, time-varying delays and unknown parameters are also considered. Finally, the applications of the theoretical results are illustrated by two numerical examples.
Open Research
DATA AVAILABILITY STATEMENT
Data sharing not applicable since the article describes entirely theoretical research.
The authors declared that they have no conflicts of interest to this work.
REFERENCES
- 1Zhang W, Yu L. Output feedback stabilization of networked control systems with packet dropouts. IEEE Trans Automat Contr. 2007; 52: 1705-1710.
- 2Bai J, Lu R, Su H, Xue A. Modeling and H1 control of wireless networked control system with both delay and packet loss. J Frankl Inst. 2015; 352: 3915-3928.
- 3Wu Y, Liu T, Wu Y, Zhang Y. H∞ output tracking control for uncertain networked control systems via a switched system approach. Int J Robust Nonlinear Control. 2016; 26: 893-1156.
- 4Hu Z, Deng F. Robust
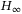control for networked systems with transmission delays and successive packet dropouts under stochastic sampling. Int J Robust Nonlinear Control. 2017; 27: 84-107.
- 5Hu Z, Zhang J, Deng F, Fan Z, Qiu L. A discretization approach to sampled-data stabilization of networked systems with successive packet losses. Internat J Robust Nonlinear Control. 2021; 31: 4589-4601.
- 6Wang Y, Zhang T, Ren J. A novel adaptive event-triggering scheme for network descriptor systems with time-delay. Internat J Robust Nonlinear Control. 2020; 30: 7947-7961.
- 7Donkers M, Heemels W, Van De Wouw N, Hetel L. Stability analysis of networked control systems using a switched linear systems approach. IEEE Trans Automat Contr. 2015; 56: 2101-2115.
- 8Tan C, Li L, Zhang H. Stabilization of networked control systems with both network-induced delay and packet dropout. Automatica. 2015; 59: 194-199.
- 9Zou L, Wang Z, Gao H, Liu X. Event-triggered state estimation for complex networks with mixed time delays via sampled data information: the continuous-time case. IEEE Trans Cybern. 2015; 45: 2804-2815.
- 10Ren Z, Cheng P, Chen J, Shi L, Zhang H. Dynamic sensor transmission power scheduling for remote state estimation. Automatica. 2014; 50: 1235-1242.
- 11Wang Z, Yang F, Ho DW, Liu X. Robust H
control for networked systems with random packet losses. IEEE Trans Syst Man Cybern B Cybern. 2007; 37: 916-924.
- 12Tang Y, Gao H, Kurths J. Robust H
self-triggered control of networked systems under packet dropouts. IEEE Trans Cybern. 2016; 46: 3294-3305.
- 13Liu A, Zhang W, Yu L, Liu S, Chen M. New results on stabilization of networked control systems with packet disordering. Automatica. 2015; 52: 255-259.
- 14Shi Y, Yu B. Robust mixed H
/H
control of networked control systems with random time delays in both forward and backward communication links. Automatica. 2011; 47: 754-760.
- 15Yang X, Zhu Q. Stabilization of stochastic functional differential systems by steepest descent feedback controls. IET Control Theory Appl. 2021; 15: 805-813.
- 16Deng F, Luo Q, Mao X. Stochastic stabilization of hybrid differential equations. Automatica. 2012; 48: 2321-2328.
- 17Zhao Y, Zhu Q. Stabilization by delay feedback control for highly nonlinear switched stochastic systems with time delays. Int J Robust Nonlinear Control. 2021; 31: 3070-3089.
- 18Mao X. Stabilization of continuous-time hybrid stochastic differential equations by discrete-time feedback control. Automatica. 2013; 49: 3677-3681.
- 19Mao X, Liu W, Hu L, Luo Q, Lu J. Stabilization of hybrid stochastic differential equations by feedback control based on discrete-time state observations. Syst Control Lett. 2014; 73: 88-95.
- 20Chen W, Xu S, Zou Y. Stabilization of hybrid neutral stochastic differential delay equations by delay feedback control. Syst Control Lett. 2016; 88: 1-13.
- 21Song G, Zeng B, Luo Q, Mao X. Stabilisation of hybrid stochastic differential equations by feedback control based on discrete-time observations of state and mode. IET Control Theory Appl. 2017; 11: 301-307.
- 22Zhu Q, Zhang Q. pth moment exponential stabilisation of hybrid stochastic differential equations by feedback controls based on discrete-time state observations with a time delay. IET Control Theory Appl. 2017; 11: 1992-2003.
- 23Zhu Q. Stabilization of stochastic nonlinear delay systems with exogenous disturbances and the event-triggered feedback control. IEEE Trans Automat Contr. 2019; 64: 3764-3771.
- 24Gao Y, Sun X, Wen C, Wang W. Event-triggered control for stochastic nonlinear systems. Automatica. 2018; 95: 534-538.
- 25Quevedo D, Gupta V, Ma W, Yuksel S. Stochastic stability of event-triggered anytime control. IEEE Trans Automat Contr. 2014; 59: 3373-3379.
- 26Anderson R, Milutinovic D, Dimarogonas D. Self-triggered sampling for second-moment stability of state-feedback controlled SDE systems. Automatica. 2015; 54: 8-15.
- 27Wu L, Gao Y, Liu J, Li H. Event-triggered sliding mode control of stochastic systems via output feedback. Automatica. 2017; 82: 79-92.
- 28Wang Y, Zheng W, Zhang H. Dynamic event-based control of nonlinear stochastic systems. IEEE Trans Automat Contr. 2017; 62: 6544-6551.
- 29Boyd S, Ghaoui L, Feron E, Balakrishnan V. Linear Matrix Inequalities in System and Control Theory. SIAM; 1994.
10.1137/1.9781611970777 Google Scholar
- 30Zhu Q, Cao J. Exponential stability of stochastic neural networks with both Markovian jump parameters and mixed time delays. IEEE Trans Syst Man Cybern B Cybern. 2011; 41: 341-353.
- 31Léchappé V, Moulay E, Plestan F, Han Q. Discrete predictor-based event-triggered control of networked control systems. Automatica. 2019; 107: 281-288.
- 32Borgers DP, Heemels W. Event-separation properties of event-triggered control systems. IEEE Trans Automat Contr. 2014; 59: 2644-2656.
- 33Donkers MCF, Heemels WPMH. Output-based event-triggered control with guaranteed-gain and improved and decentralized event-triggering. IEEE Trans Automat Contr. 2012; 57: 1362-1376.
- 34Linsenmayer S, Dimarogonas DV, Allgŏwer F. Periodic event-triggered control for networked control systems based on non-monotonic Lyapunov functions. Automatica. 2019; 106: 35-46.
- 35Lunze J, Lehmann D. A state-feedback approach to event-based control. Automatica. 2010; 46: 211-215.
- 36Tabuada P. Event-triggered real-time scheduling of stabilizing control tasks. IEEE Trans Automat Contr. 2007; 52: 1680-1685.
- 37Xie Y, Lin Z. Event-triggered global stabilization of general linear systems with bounded controls. Automatica. 2019; 107: 241-254.
- 38Tallapragada P, Chopra N. On event triggered tracking for nonlinear systems. IEEE Trans Automat Contr. 2013; 58: 2343-2348.
- 39Garcia E, Antsaklis P. Model-based event-triggered control for systems with quantization and time-varying network delays. IEEE Trans Automat Contr. 2013; 58: 422-434.
- 40Poveda JI, Teel AR. A robust event-triggered approach for fast sampled-data extremization and learning. IEEE Trans Automat Contr. 2017; 62: 4949-4964.
- 41Dimarogonas D, Frazzoli E, Johansson K. Distributed event-triggered control for multi-agent systems. IEEE Trans Automat Contr. 2012; 57: 1291-1297.
- 42Song R, Wang B, Zhu Q. Delay-dependent stability of nonlinear hybrid neutral stochastic differential equations with multiple delays. Int J Robust Nonlinear Control. 2021; 31: 250-267.
- 43Zhang M, Zhu Q. Stability analysis for switched stochastic delayed systems under asynchronous switching: a relaxed switching signal. Int J Robust Nonlinear Control. 2020; 30(18): 8278-8298.
- 44Cao W, Zhu Q. Razumikhin-type theorem for pth exponential stability of impulsive stochastic functional differential equations based on vector Lyapunov function. Nonlinear Anal Hybrid Syst. 2021; 39:100983.
- 45 Kong F, Zhu Q, Huang T. New fixed-time stability lemmas and applications to the discontinuous fuzzy inertial neural networks. IEEE Trans Fuzzy Syst. 2020. https://doi.org/10.1109/TFUZZ.2020.3026030
- 46Gao L, Cao Z, Zhang M, Zhu Q. Input-to-state stability for hybrid delayed systems with admissible edge-dependent switching signals. J Frankl Inst. 2020; 357: 8823-8850.
- 47 King D, Zhu Q. Fuzzy intermittent extended dissipative control for delayed distributed parameter systems with stochastic disturbance: a spatial point sampling approach. IEEE Trans Fuzzy Syst. 2021. https://doi.org/10.1109/TFUZZ.2021.3065524
