In this article, a robust model predictive control (MPC) procedure for quasi-linear parameter varying (qLPV) systems is proposed. The novelty resides in considering a recursive extrapolation algorithm to estimate the values of the scheduling parameters along the prediction horizon 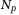, which fastens the sluggish performances achieved with the robust qLPV MPCs from the literature. The bounds on the estimation errors of the scheduling parameters through 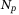are taken into account by the robust MPC, which solves an online min-max problem: first, a constrained convex program is resolved in order to determine the worst-case bound on the cost function and, subsequently, a second constrained quadratic program is solved to minimize this worst-case cost function with respect to a control sequence vector. Since the bounds on the estimation error for the scheduling parameters are usually much smaller than the bounds on the actual scheduling parameter, the conservativeness of the solution is quite reduced. Recursive feasibility and stability of the proposed algorithm are demonstrated with dissipativity arguments given in the form of a linear matrix inequality remedy, which determines the zone of attraction for which input-to-state stability is ensured. The nonlinear temperature regulation problem of a flat solar collector is considered as a case study. Using a realistic simulation benchmark, the proposed technique is compared to other robust min-max LPV MPC algorithms from the literature, proving itself efficient while achieving good performances.