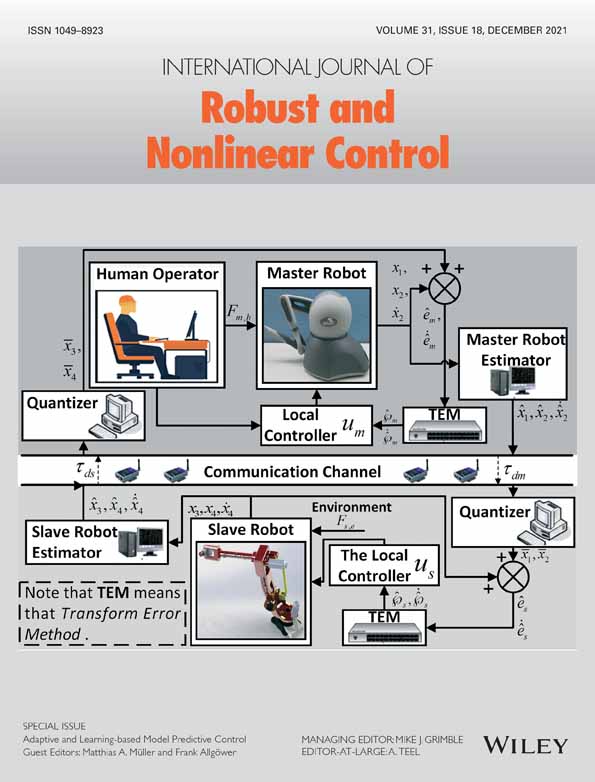
Robust saddle-point criterion in second-order partial differential equation and partial differential inequation constrained control problems
Abstract
In this article, for a given class of multi-dimensional scalar variational control problems (named 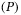 ) with mixed constraints implying second-order partial differential equations and inequations, we introduce an auxiliary (modified) class of variational control problems (named
) with mixed constraints implying second-order partial differential equations and inequations, we introduce an auxiliary (modified) class of variational control problems (named 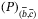 ), which is much easier to study, and provide some characterization results of
), which is much easier to study, and provide some characterization results of 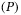 and
and 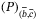 by using the notions of normal weak robust optimal solution and robust saddle-point associated with a Lagrange functional corresponding to
by using the notions of normal weak robust optimal solution and robust saddle-point associated with a Lagrange functional corresponding to 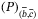 . For this aim, we consider scalar multiple integral cost functionals and the notion of convexity associated with a multiple integral functional driven by an uncertain multi-time controlled second-order Lagrangian.
. For this aim, we consider scalar multiple integral cost functionals and the notion of convexity associated with a multiple integral functional driven by an uncertain multi-time controlled second-order Lagrangian.
CONFLICT OF INTEREST
The author declared no conflict of interest to this work.
Open Research
DATA AVAILABILITY STATEMENT
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.



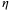 -objective function under invexity
-objective function under invexity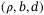 -invexity and
-invexity and 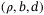 -pseudoinvexity in interval-valued optimization problems
-pseudoinvexity in interval-valued optimization problems