Mean square exponential stabilization of uncertain time-delay stochastic systems with fractional Brownian motion

Majid Parvizian,

Majid Parvizian

School of Electrical and Computer Engineering, Tarbiat Modares University, Tehran, Iran

Search for more papers by this author

Khosro Khandani,

Corresponding Author

Khosro Khandani

[email protected]

orcid.org/0000-0002-1762-3541

Department of Electrical Engineering, Faculty of Engineering, Arak University, Arak, Iran

Correspondence

Khosro Khandani, Department of Electrical Engineering, Faculty of Engineering, Arak University, Arak, Iran.

Email: [email protected]

Search for more papers by this author

Majid Parvizian,

Majid Parvizian

School of Electrical and Computer Engineering, Tarbiat Modares University, Tehran, Iran

Search for more papers by this author

Khosro Khandani,

Corresponding Author

Khosro Khandani

[email protected]

orcid.org/0000-0002-1762-3541

Department of Electrical Engineering, Faculty of Engineering, Arak University, Arak, Iran

Correspondence

Khosro Khandani, Department of Electrical Engineering, Faculty of Engineering, Arak University, Arak, Iran.

Email: [email protected]

Search for more papers by this author

First published: 07 September 2021

https://doi.org/10.1002/rnc.5764

Citations: 7

Share a link

Email
Wechat
Bluesky

Abstract

This article is concerned with exponential mean square stabilization of stochastic systems driven by fractional Brownian motion subject to state-delay and uncertainties by sliding mode control. By applying the proposed method, the states of the system reach the sliding surface in finite time. Then, some sufficient conditions are given in terms of linear matrix inequalities (LMIs) to guarantee the mean-square exponential stability of the sliding motion. The LMI conditions for mean-square exponential stability of the sliding mode dynamics are derived by constructing a novel Lyapunov functional. Finally, a simulation example is presented which corroborates the accuracy of the results.

CONFLICT OF INTEREST

The authors declared there is no conflicts of interest to this work.

Open Research

DATA AVAILABILITY STATEMENT

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

REFERENCES

1Poznyak AS. Stochastic sliding mode control and state estimation. Advances in Variable Structure Systems and Sliding Mode Control—Theory and Applications. Springer; 2018: 57-100.
10.1007/978-3-319-62896-7_3
Google Scholar
2Park K, Willinger W. Self-Similar Network Traffic and Performance Evaluation. Wiley; 2000.
10.1002/047120644X
Google Scholar
3Calif R, Schmitt FG. Modeling of atmospheric wind speed sequence using a lognormal continuous stochastic equation. J Wind Eng Ind Aerod. 2012; 109: 1-8.
10.1016/j.jweia.2012.06.002
Web of Science® Google Scholar
4Meerschaert MM, Sabzikar F. Tempered fractional Brownian motion. Stat Probab Lett. 2013; 83: 2269-2275.
10.1016/j.spl.2013.06.016
Web of Science® Google Scholar
5Novak MM. Paradigms of Complexity: Fractals and Structures in the Sciences. World Scientific; 2000.
10.1142/4409
Google Scholar
6Pei B, Bin Y, Xu JL. Wu, stochastic averaging for stochastic differential equations driven by fractional Brownian motion and standard Brownian motion. Appl Math Lett. 2020; 100:106006.
10.1016/j.aml.2019.106006
Web of Science® Google Scholar
7Xu L, Li Z. Stochastic fractional evolution equations with fractional brownian motion and infinite delay. Appl Math Comput. 2018; 336: 36-46.
10.1016/j.amc.2018.04.060
Web of Science® Google Scholar
8Sathiyaraj T, Wang J, Balasubramaniam P. Ulam's stability of Hilfer fractional stochastic differential systems. Eur Phys J Plus. 2019; 134(12): 605.
10.1140/epjp/i2019-12952-y
Web of Science® Google Scholar
9Zeng C, Yang Q, Chen YQ. Solving nonlinear stochastic differential equations with fractional Brownian motion using reducibility approach. Nonlinear Dyn. 2012; 67: 2719-2726.
10.1007/s11071-011-0183-3
Web of Science® Google Scholar
10Nguyen D. Asymptotic behavior of linear fractional stochastic differential equations with time-varying delays. Commun Nonlinear Sci. 2014; 19: 1-7.
10.1016/j.cnsns.2013.06.004
Web of Science® Google Scholar
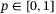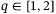11Arthi G, Park JH, Jung HY. Existence and exponential stability for neutral stochastic integrodifferential equations with impulses driven by a fractional Brownian motion. Commun Nonlinear Sci Numer Simul. 2016; 32: 145-157.
10.1016/j.cnsns.2015.08.014
Web of Science® Google Scholar
12Khandani K, Majd VJ, Tahmasebi M. Comments on "solving nonlinear stochastic differential equations with fractional Brownian motion using reducibility approach" [Nonlinear Dyn. 67, 2719–2726 (2012)]. Nonlinear Dyn. 2015; 82(3): 1605-1607.
10.1007/s11071-015-2249-0
Web of Science® Google Scholar
13Sathiyaraj T, Balasubramaniam P. Controllability of fractional neutral stochastic integrodifferential inclusions of order $urn:x-wiley:10498923:media:rnc5764:rnc5764-math-0229$ , $urn:x-wiley:10498923:media:rnc5764:rnc5764-math-0230$ with fractional Brownian motion. Eur Phys J Plus. 2016; 131(10): 1-17.
10.1140/epjp/i2016-16357-2
Web of Science® Google Scholar
14Sathiyaraj T, Balasubramaniam P. Controllability of fractional higher order stochastic integrodifferential systems with fractional Brownian motion. ISA Trans. 2018; 82: 107-119.
10.1016/j.isatra.2017.11.005
CAS PubMed Web of Science® Google Scholar
15Gao Q, Feng G, Liu L, Qiu J, Wang Y. An ISMC approach to robust stabilization of uncertain stochastic time-delay systems. IEEE Trans Ind Electron. 2014; 61: 6986-6994.
10.1109/TIE.2014.2314057
Web of Science® Google Scholar
16Zhang Q, Zhang J, Wang Y. Sliding-mode control for singular Markovian jump systems with Brownian motion based on stochastic sliding mode surface. IEEE Trans Syst Man Cybern Syst. 2019; 49(3): 494-505.
10.1109/TSMC.2017.2713417
Web of Science® Google Scholar
17Song J, Niu Y, Zou Y. A parameter-dependent sliding mode approach for finite-time bounded control of uncertain stochastic systems with randomly varying actuator faults and its application to a parallel active suspension system. IEEE Trans Ind Electron. 2018; 65(10): 8124-8132.
10.1109/TIE.2018.2801801
Web of Science® Google Scholar
18Zhang X, Ding X, Zhou W, Sun Y. Structure-triggered asymptotical synchronization for nonidentical generalized stochastic systems with Markovian jumping parameter based on sliding mode control. Int J Robust Nonlinear Control. 2020; 30(16): 6414-6432.
10.1002/rnc.5102
Web of Science® Google Scholar
19Yao D, Zhang B, Li P, Li H. Event-triggered sliding mode control of discrete-time Markov jump systems. IEEE Trans Syst Man Cybern Syst. 2019; 49(10): 2016-2025.
10.1109/TSMC.2018.2836390
Web of Science® Google Scholar
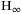20Niu Y, Ho DWC, Wang X. Robust $urn:x-wiley:10498923:media:rnc5764:rnc5764-math-0231$ control for nonlinear stochastic systems: a sliding mode approach. IEEE Trans Automat Contr. 2008; 53(7): 1695-1701.
10.1109/TAC.2008.929376
Web of Science® Google Scholar
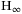21Ma Y, Liu Y. Finite-time $urn:x-wiley:10498923:media:rnc5764:rnc5764-math-0232$ sliding mode control for uncertain singular stochastic system with actuator faults and bounded transition probabilities. Nonlinear Anal-Hybri. 2019; 33: 52-75.
10.1016/j.nahs.2019.02.002
Web of Science® Google Scholar
22Jia F, Hu J, Feng L, Chen D, Tan C. Adaptive sliding-mode-based control for stochastic nonlinear systems subject to probabilistic interval delay: a delay-fractioning method. J Franklin Inst. 2020; 357(2): 1002-1025.
10.1016/j.jfranklin.2019.10.017
Web of Science® Google Scholar
23Ma R, Yan T. Sliding mode tracking control using finite-time differentiator in high-orders nonlinear systems with output stochastic signals. Int J Robust Nonlinear Control. 2020; 30(16): 6961-6977.
10.1002/rnc.5152
Web of Science® Google Scholar
24Ma L, Wang C, Ding S, Dong L. Integral sliding mode control for stochastic Markovian jump system with time-varying delay. Neurocomputing. 2016; 179: 118-125.
10.1016/j.neucom.2015.11.071
Web of Science® Google Scholar
25Khandani K, Majd VJ, Tahmasebi M. Integral sliding mode control for robust stabilization of uncertain stochastic time-delay systems driven by fractional Brownian motion. Int J Syst Sci. 2017; 48(4): 828-837.
10.1080/00207721.2016.1216201
Web of Science® Google Scholar
26Khandani K, Majd VJ, Tahmasebi M. Robust stabilization of uncertain time-delay systems with fractional stochastic noise using the novel fractional stochastic sliding approach and its application to stream water quality regulation. IEEE Trans Automat Contr. 2016; 62(4): 1742-1751.
10.1109/TAC.2016.2594261
Web of Science® Google Scholar
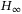27Shi L, Zhang W. Robust $urn:x-wiley:10498923:media:rnc5764:rnc5764-math-0233$ filtering and control for a class of linear systems with fractional stochastic noise. Physica A. 2019; 526:120958.
10.1016/j.physa.2019.04.194
Web of Science® Google Scholar
28Khandani K. A sliding mode observer design for uncertain fractional Ito stochastic systems with state delay. Int J Gen Syst. 2018; 48(1): 48-65.
10.1080/03081079.2018.1534846
Web of Science® Google Scholar
29Boyd S, El Ghaoui L, Feron E, Balakrishnan V. Linear Matrix Inequalities in System and Control Theory. Vol 15. Siam; 1994.
10.1137/1.9781611970777
Google Scholar
30Teel AR, Subbaraman A, Sferlazza A. Stability analysis for stochastic hybrid systems: a survey. Automatica. 2014; 50(10): 2435-2456.
10.1016/j.automatica.2014.08.006
Web of Science® Google Scholar