Aufsatz
Thermodynamik der elektrochemischen Lithiumspeicherung
Prof. Joachim Maier,
Corresponding Author
Prof. Joachim Maier
Max-Planck-Institut für Festkörperforschung, Heisenbergstraße 1, 70569 Stuttgart (Deutschland)
Max-Planck-Institut für Festkörperforschung, Heisenbergstraße 1, 70569 Stuttgart (Deutschland)Search for more papers by this authorProf. Joachim Maier,
Corresponding Author
Prof. Joachim Maier
Max-Planck-Institut für Festkörperforschung, Heisenbergstraße 1, 70569 Stuttgart (Deutschland)
Max-Planck-Institut für Festkörperforschung, Heisenbergstraße 1, 70569 Stuttgart (Deutschland)Search for more papers by this authorAbstract
Die Thermodynamik der elektrochemischen Lithiumspeicherung wird explizit unter dem Aspekt betrachtet, dass es die Punktdefekte sind, die Speicherung ermöglichen. Während Li-Defekte beweglich sind, müssen die meisten der anderen Punktdefekte angesichts der im Vergleich zum Schmelzpunkt der Elektrodenmaterialien niedrigen Prozesstemperatur als eingefroren betrachtet werden. Die Betrachtungsebene der Defektchemie ist für das Verständnis der Lade-/Entladekurven im Gleichgewicht essentiell. Auf dieser Grundlage können Einphasen- und Mehrphasenspeichermechanismen bezüglich theoretischer Speicherkapazität und Spannung diskutiert werden. Von außerordentlichem Interesse auf dem Gebiet der Lithiumbatterien sind metastabile Materialien, vor allem nanokristalliner und amorpher Natur. Die Thermodynamik in Bezug auf Speicherung und Spannung, auch an Grenzflächen, verdient dementsprechend eine spezielle Behandlung. Außerdem wird der Zusammenhang zwischen reversibler Zellspannung und Lithiumgehalt für den neuartigen “Job-Sharing”-Mechanismus abgeleitet. Für die klassischen Arten der Speicherung werden thermodynamische Unterschiede zwischen Kathoden und Anoden herausgearbeitet. Dies geschieht mit speziellem Fokus auf der Suche nach neuen Materialien. Da sich dieser Aufsatz auf den Gleichgewichtszustand konzentriert, werden Phänomene unter Stromleitung nur am Rande diskutiert.
References
- 1J. B. Goodenough in Encyclopedia of Sustainability Science and Technology (Hrsg.: ), Springer, New York, 2012.
- 2M. Armand, J. M. Tarascon, Nature 2008, 451, 652–657.
- 3P. G. Bruce, B. Scrosati, J. M. Tarascon, Angew. Chem. 2008, 120, 2972–2989;
10.1002/ange.200702505 Google ScholarAngew. Chem. Int. Ed. 2008, 47, 2930–2946.
- 4J. Maier in Die Zukunft der Energie, Die Antwort der Wissenschaft, Ein Report der Max-Planck-Gesellschaft (Hrsg.: ), C. H. Beck, München, 2008, S. 282–294.
- 5J. Maier, Nat. Mater. 2005, 4, 805–815.
- 6J. Maier, J. Power Sources 2007, 174, 569–574.
- 7F. A. Kröger, Chemistry of Imperfect Crystals, North-Holland, Amsterdam, 1964.
10.1063/1.3051186 Google Scholar
- 8F. A. Kröger, H. J. Vink, Solid State Physics, Vol. 3 (Hrsg.: ), Academic Press, New York, 1956, S. 307–435.
- 9J. Maier, Solid State Ionics 2001, 143, 17–23.
- 10J. Maier, Physical Chemistry of Ionic Materials, Ions and Electrons in Solids, Wiley, Hoboken, 2004.
10.1002/0470020229 Google Scholar
- 11M. S. Whittingham, F. R. Gamble, Mater. Res. Bull. 1975, 10, 363–372.
- 12K. Mizushima, P. C. Jones, P. J. Wiseman, J. B. Goodenough, Mater. Res. Bull. 1980, 15, 783–789.
- 13A. K. Padhi, K. S. Nanjundaswamy, J. B. Goodenough, J. Electrochem. Soc. 1997, 144, 1188–1194.
- 14I. A. Courtney, J. R. Dahn, J. Electrochem. Soc. 1997, 144, 2045–2052.
- 15H. Li, X. J. Huang, L. Q. Chen, Solid State Ionics 1999, 123, 189–197.
- 16P. Poizot, S. Laruelle, S. Grugeon, L. Dupont, J. M. Tarascon, Nature 2000, 407, 496–499.
- 17P. Balaya, H. Li, L. Kienle, J. Maier, Adv. Funct. Mater. 2003, 13, 621–625.
- 18F. Badway, F. Cosandey, N. Pereira, G. G. Amatucci, J. Electrochem. Soc. 2003, 150, A 1318–A1327.
- 19H. Li, P. Balaya, J. Maier, J. Electrochem. Soc. 2004, 151, A 1878–A1885.
- 20J. Jamnik, J. Maier, Phys. Chem. Chem. Phys. 2003, 5, 5215–5220.
- 21Y. F. Zhukovskii, P. Balaya, E. A. Kotomin, J. Maier, Phys. Rev. Lett. 2006, 96, 058302.
- 22J. Maier, Faraday Discuss. 2007, 134, 51–56.
- 23N. A. Kaskhedikar, J. Maier, Adv. Mater. 2009, 21, 2664–2680.
- 24Die Tatsache, dass der Energieeintrag/Energiegewinn proportional zum Höhenunterschied h als entscheidenden Parameter ist, obwohl das Gravitationspotential proportional zu 1/r (mit r als Abstand zwischen den Gravitationszentren der Massen) ist, stellt keinen Widerspruch dar. Der Grund dafür ist, dass h relativ zu einem Nullpunkt R (Meeresspiegel) definiert ist, sodass h≪R. Dann führt die Taylor-Entwicklung auf
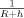≅const−h/R2.
- 25Um die äquivalente Energiemenge durch Bewegung der gleichen Menge Li im Gravitationsfeld speichern zu können, die nötig ist, um Li in einer Batterie bei einer Spannung von 1 V von der Positivelektrode zur Negativelektrode zu bringen, reichen die Höhenunterschiede auf der Erdoberfläche nicht aus.
- 26Während die Begriffe negative und positive Elektrode für das Material klar definiert sind, werden die Rollen der Anode und Kathode vom Lade- zum Entladeprozess vertauscht. Hier verwenden wir die bekannte, aber unpräzise Konvention, sich auf das Entladen zu beziehen und die Negativelektrode als Anode und die Positivelektrode als Kathode zu bezeichnen.
- 27Da sie chemisch identisch sind und eine hohe elektronische Konzentration aufweisen, kann man auch direkt die Unterschiede in den elektrischen Potentialen betrachten.
- 28Dies folgt aus der Tatsache, dass im Gleichgewicht kein Li+-Fluss (
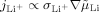) existiert. Dies schließt ein Produkt aus 
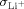(Li+-Leitfähigkeit) und 
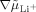ein, das den Wert null annimmt. Für 
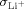ungleich null bedeutet dies 
.
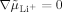- 29J. Maier in Modern Aspects of Electrochemistry (Hrsg.: ), Kluwer/Plenum, New York, 2005, S. 1–173;
10.1007/0-387-25838-8_1 Google ScholarJ. Maier in Modern Aspects of Electrochemistry (Hrsg.: ), Springer, New York, 2007, S. 1–138.10.1007/978-0-387-46108-3_1 Google Scholar
- 30L. D. Burke, O. J. Murphy, J. Electroanal. Chem. Interfacial Electrochem. 1979, 96, 19–27.
- 31D. Muñoz-Rojas, M. Casas-Cabanas, E. Baudrin, Solid State Ionics 2009, 180, 308–313.
- 32Siehe Lehrbücher über chemische Thermodynamik. Wenn sich das chemische Potential mit wachsendem Li-Gehalt verringern würde, wäre der Gleichgewichtszustand natürlich nicht stabil bezüglich der Variation des Li-Gehaltes.
- 33Das chemische Potential von Lithium kann auch mittels neutraler Li-Defekte ausgedrückt werden (
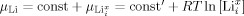, verdünnte Defekte vorausgesetzt).
- 34Wir ignorieren Einbau durch Substitution, da dies 1) eine hohe Mobilität des zu ersetzenden Ions erfordert und 2) zu Komplikationen bei Stromumkehr führen würde.
- 35C. Wagner, W. Schottky, Z. Phys. Chem. 1930, B11, 163–210.
- 36C. Wagner, Z. Phys. Chem. 1936, B32, 447–462.
- 37Bezüglich der Aktivitätskoeffizienten von Punktdefekten wird der Leser auf A. Lidiard, Phys. Rev. 1954, 94, 29–37 verwiesen.
- 38
- 38aJ. Maier, Z. Phys. Chem. 2005, 219, 35–46;
- 38bJ. Maier, Z. Phys. Chem. 2012, 226, 863–870.
- 39R. Merkle, J. Maier, Phys. Chem. Chem. Phys. 2003, 5, 2297–2303.
- 40Zugunsten einer symmetrischen Form zu Gleichung (21) mag es ratsam sein, eine Massenwirkungskonstante
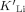einzuführen, die definiert ist durch 
. Es ist zu beachten, dass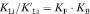 
- 41R. Waser, J. Am. Ceram. Soc. 1991, 74, 1934–1940.
- 42J. Maier, Phys. Chem. Chem. Phys. 2003, 5, 2164–2173.
- 43P. Kofstad, Nonstoichiometry, Diffusion and Electrical Conductivity in Binary Oxides, Wiley, New York, 1972.
- 44K. Hauffe, Reaktionen in und an festen Stoffen, Springer, Berlin, 1955.
10.1007/978-3-642-52680-0 Google Scholar
- 45G. Brouwer, Philips Res. Rep. 1954, 9, 366–376.
- 46N. Valverde, Z. Phys. Chem. 1970, 70, 113–127.
- 47R. Merkle, J. Maier, Angew. Chem. 2008, 120, 3936–3958;
10.1002/ange.200700987 Google ScholarAngew. Chem. Int. Ed. 2008, 47, 3874–3894.
- 48S. R. Bishop, T. S. Stefanik, H. L. Tuller, Phys. Chem. Chem. Phys. 2011, 13, 10165–10173.
- 49J. Maier, R. Amin, J. Electrochem. Soc. 2008, 155, A 339–A344.
- 50J.-Y. Shin, D. Samuelis, J. Maier, Solid State Ionics 2012, 225, 590–593.
- 51J. Maier, Phys. Chem. Chem. Phys. 2009, 11, 3011–3022.
- 52P. Debye, E. Hückel, Phys. Z. 1923, 24, 185–206; P. Debye, E. Hückel, Phys. Z. 1923, 24, 305–325.
- 53In einem System aus n Komponenten
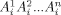für i, welches von 1 bis 2 läuft, müssen alle n chemischen Potentiale μ(Ai) im absoluten Gleichgewicht denselben Wert haben. Da eines dieser Potentiale die Zellspannung bestimmt, folgt die Lösung aus einem Satz von n Gleichungen mit n Unbekannten. Für eine Anwendung von EMK-Messungen in Zellen mit oxidischem Festelektrolyten siehe z. B.: W. Piekarczyk, W. Weppner, A. Rabenau, Z. Naturforsch. A 1979, 34, 430–436.
- 54N. A. Godshall, I. D. Raistrick, R. A. Huggins, J. Electrochem. Soc. 1984, 131, 543–549.
- 55Für winzige Partikelgrößen kann der amorphe Zustand sogar eine geringere Gibbs-Energie als der nanokristalline Zustand haben. Dies ist immer dann der Fall, wenn die Freie Oberflächenenergie des amorphen Zustands gegenüber der kristallinen Situation so viel geringer ist, dass die höhere Freie Volumenenergie überkompensiert wird. Siehe beispielsweise: M. Pitcher, S. V. Ushakov, A. Navrotsky, J. Am. Ceram. Soc. 2005, 88, 160–167.
- 56R. Defay, I. Prigogine, A. Bellemans, H. Everett, Surface Tension and Adsorption, Wiley, New York, 1960.
- 57A. I. Rusanov, Phasengleichgewichte und Grenzflächenerscheinungen, Akademie Verlag, Berlin, 1978.
10.1515/9783112531709 Google Scholar
- 58J. Maier, Adv. Mater. 2009, 21, 2571–2585.
- 59J. Maier, Solid State Ionics 2002, 154, 291–301.
- 60T. L. Hill, Thermodynamics of Small Systems, W. A. Benjamin, New York, 1963.
- 61D. Kramer, J. Weissmueller, Surf. Sci. 2007, 601, 3042–3051.
- 62Y. T. Cheng, M. W. Verbrugge, J. Appl. Phys. 2008, 104, 083521–083521.
- 63L. D. Landau, E. M. Lifshitz, Statistical Physics, Vol. 5 (Course of Theoretical Physics), Pergamon, Oxford, 1968.
- 64Lit. [38a].
- 65P. Buffat, J.-P. Borel, Phys. Rev. A 1976, 13, 2287–2298.
- 66P. Knauth, G. Schwitzgebel, A. Tschöpe, S. Villain, J. Solid State Chem. 1998, 140, 295–299.
- 67A. Schroeder, J. Fleig, H. Drings, R. Wuerschum, J. Maier, W. Sitte, Solid State Ionics 2004, 173, 95–101.
- 68P. Balaya, J. Maier, Phys. Chem. Chem. Phys. 2010, 12, 215–219.
- 69C. Zhu, Dissertation, Stuttgart, 2012.
- 70O. Delmer, P. Balaya, L. Kienle, J. Maier, Adv. Mater. 2008, 20, 501–505.
- 71O. Delmer, J. Maier, Phys. Chem. Chem. Phys. 2009, 11, 6424–6429.
- 72Während die Interpretation der EMK im Zwei-Phasen-System in Lit. [70] und [71] präzise ist, überschätzt die Betrachtung des Ein-Phasen-Regimes basierend auf einem konstanten Δ die Kapillareffekte, wie in diesem Abschnitt dargestellt.
- 73D. Wagner, J. Optoelectron. Adv. Mater. 2004, 6, 345–347.
- 74M. Wagemaker, F. M. Mulder, A. Van der Ven, Adv. Mater. 2009, 21, 2703–2709.
- 75N. Meethong, H.-Y. S. Huang, S. A. Speakman, W. C. Carter, Y.-M. Chiang, Adv. Funct. Mater. 2007, 17, 1115–1123.
- 76J. Cahn, J. Hilliard, J. Chem. Phys. 1958, 28, 258–267.
- 77M. Wagemaker, B. L. Ellis, D. Luetzenkirchen-Hecht, F. M. Mulder, L. F. Nazar, Chem. Mater. 2008, 20, 6313–6315.
- 78L. Gu, C. Zhu, H. Li, Y. Yu, C. L. Li, S. Tsukimoto, J. Maier, Y. Ikuhara, J. Am. Chem. Soc. 2011, 133, 4661–4663.
- 79L. Suo, W. Han, X. Lu, L. Gu, Y. Hu, H. Li, D. Chen, L. Chen, S. Tsukimoto, Y. Ikuhara, Phys. Chem. Chem. Phys. 2012, 14, 5363–5367.
- 80Lit. [20].
- 81Lit. [5].
- 82J. Maier, Prog. Solid State Chem. 1995, 23, 171–263.
- 83E. Peled, J. Electrochem. Soc. 1979, 126, 2047–2051.
- 84D. Aurbach, J. Power Sources 2000, 89, 206–218.
- 85Siehe z. B. Lit. [82].
- 86J. Maier, Ber. Bunsen-Ges. Phys. Chem. 1985, 89, 355–362.
- 87S. R. de Groot, Thermodynamics of Irreversible Processes, North-Holland, Amsterdam, 1960.
- 88J.-Y. Shin, D. Samuelis, J. Maier, Adv. Funct. Mater. 2011, 21, 3464–3472.
- 89A. J. Bhattacharyya, J. Maier, Adv. Mater. 2004, 16, 811–814.
- 90Y.-G. Guo, Y.-S. Hu, W. Sigle, J. Maier, Adv. Mater. 2007, 19, 2087–2091.
- 91F.-F. Cao, Y.-G. Guo, S.-F. Zheng, X.-L. Wu, L.-Y. Jiang, R.-R. Bi, L.-J. Wan, J. Maier, Chem. Mater. 2010, 22, 1908–1914.
- 92Y. Yu, L. Gu, C. Wang, A. Dhanabalan, P. A. van Aken, J. Maier, Angew. Chem. 2009, 121, 6607–6611; Angew. Chem. Int. Ed. 2009, 48, 6485–6489.
- 93Y. Yu, L. Gu, C. Zhu, P. A. van Aken, J. Maier, J. Am. Chem. Soc. 2009, 131, 15984–15985.
- 94H. Wu, G. Chan, J. W. Choi, I. Ryu, Y. Yao, M. T. McDowell, S. W. Lee, A. Jackson, Y. Yang, L. Hu, Y. Cui, Nat. Nanotechnol. 2012, 7, 309–314.
- 95Y.-S. Hu, P. Adelhelm, B. M. Smarsly, S. Hore, M. Antonietti, J. Maier, Adv. Funct. Mater. 2007, 17, 1873–1878.
- 96Y.-S. Hu, X. Liu, J.-O. Müller, R. Schlögl, J. Maier, D.-S. Su, Angew. Chem. 2009, 121, 216–220; Angew. Chem. Int. Ed. 2009, 48, 210–214.
- 97L. Bazin, S. Mitra, P. L. Taberna, P. Poizot, M. Gressier, M. J. Menu, A. Barnabe, P. Simon, J.-M. Tarascon, J. Power Sources 2009, 188, 578–582; M. Morcrette, P. Rozier, L. Dupont, E. Mugnier, L. Sannier, J. Galy, J.-M. Tarascon, Nat. Mater. 2003, 2, 755–761.
- 98A. R. Armstrong, G. Armstrong, J. Canales, R. Garcia, P. G. Bruce, Adv. Mater. 2005, 17, 862–865.
- 99S. Yang, X. Feng, L. Wang, K. Tang, J. Maier, K. Müllen, Angew. Chem. 2010, 122, 4905–4909; Angew. Chem. Int. Ed. 2010, 49, 4795–4799.
- 100W. Dreyer, J. Jamnik, C. Guhlke, R. Huth, J. Moškon, M. Gaberšček, Nat. Mater. 2010, 9, 448–453.
- 101C. Delmas, M. Maccario, L. Croguennec, F. Le Cras, F. Weill, Nat. Mater. 2008, 7, 665–671.
- 102R. Malik, F. Zhou, G. Ceder, Nat. Mater. 2011, 10, 587–590.
- 103P. G. Bruce, S. A. Freunberger, L. J. Hardwick, J. M. Tarascon, Nat. Mater. 2012, 11, 19–29.
- 104A. Débart, A. J. Paterson, J. Bao, P. G. Bruce, Angew. Chem. 2008, 120, 4597–4600;
10.1002/ange.200705648 Google ScholarAngew. Chem. Int. Ed. 2008, 47, 4521–4524.
- 105Z.-Q. Peng, S. A. Freunberger, Y.-H. Chen, P. G. Bruce, Science 2012, 337, 563–566.
- 106>P. Hartmann, C. L. Bender, M. Vračar, A. K. Dürr, A. Garsuch, J. Janek, P. Adelhelm, Nat. Mater. 2013, 12, 228–232.
- 107X. Ji, K. T. Lee, L. F. Nazar, Nat. Mater. 2009, 8, 500–506.
- 108T. Oshima, M. Kajita, A. Okuno, Int. J. Appl. Ceram. Technol. 2004, 1, 269–276.
- 109N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto, A. Mitsui, Nat. Mater. 2011, 10, 682–686.
- 110A. Jarosik, C. Pfaffenhuber, A. Bunde, J. Maier, Adv. Funct. Mater. 2011, 21, 3961–3966.
- 111K.-D. Kreuer, A. Wohlfarth, C. C. de Araujo, A. Fuchs, J. Maier, ChemPhysChem 2011, 12, 2558–2560.
- 112M. Armand, F. Endres, D. R. MacFarlane, H. Ohno, B. Scrosati, Nat. Mater. 2009, 8, 621–629.
- 113G. Ceder, MRS Bull. 2010, 35, 693–701.
- 114G. H. Carey, J. R. Dahn, ACS Comb. Sci. 2011, 13, 186–189.
- 115A. Magasinski, P. Dixon, B. Hertzberg, A. Kvit, J. Ayala, G. Yushin, Nat. Mater. 2010, 9, 353–358.
- 116G. Derrien, J. Hassoun, S. Panero, B. Scrosati, Adv. Mater. 2007, 19, 2336–2340.
- 117Der hohe Oxidationsgrad wird am eindrucksvollsten durch den am Ende von Abschnitt 4 genannten Zusammenhang zwischen dem Gleichgewichtspartialdruck von Sauerstoff bei non-varianten Systemen und der Zellspannung widergespiegelt.
- 118Nehmen wir einen Leiter vom n-Typ als Beispiel. Was die Veränderung von μLi mit δ betrifft, so ist der interessante Term,
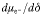dessen Wert durch χeon/ceon mit ceon=[e′] bestimmt wird (J. Maier, J. Am. Ceram. Soc. 1993, 76, 1212–1217). χeon ist der elektronische differentielle Trapping-Faktor, der durch die Valenzänderung des Dotieratoms bedingt ist, die ihrerseits mit den Massenwirkungskonstanten der internen Redoxreaktion und der Dotierkonzentration zusammenhängt. Wenn für die Reaktion Fe3+e−⇌Fe2+ die freie Elektronenkonzentration als klein im Vergleich zur Konzentration der Redoxzustände angenommen werden kann, so ist der Term proportional zu 
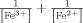und hat damit sein Maximum für [Fe3+]=[Fe2+]=m/2. Dieses drückt die Pufferkapazität bei elektronischer Veränderung aus.
- 119Diesen Aspekt betreffend herrscht ein bemerkenswertes Durcheinander in der Literatur.
- 120Siehe z. B.: C. H. P. Lupis, Chemical Thermodynamics of Materials, North-Holland, Amsterdam, 1983.
- 121Siehe z. B.: W. Schottky, Halbleiterprobleme I (Hrsg.: ), Vieweg, Braunschweig, 1954.
- 122Y.-G. Guo, Y.-S. Hu, J. Maier, Chem. Commun. 2006, 2783–2785.
Citing Literature
This is the
German version
of Angewandte Chemie.
Note for articles published since 1962:
Do not cite this version alone.
Take me to the International Edition version with citable page numbers, DOI, and citation export.
We apologize for the inconvenience.
