A mathematical and dosimetric approach to validate auto-contouring by Varian Smart segmentation for prostate cancer patients
Abstract
Purpose
The aim of this study was to quantify the discrepancies in geometrical and dosimetric impacts (in volumetric modulated arc therapy) between manually segmented (MS) contours and smart segmentation (SS) auto-contours (by Varian Eclipse Treatment Planning System SS v13.5) for prostate cancer patients.
Methods
The automated segmentation was carried out by Eclipse Treatment Planning System (Varian, version 13.5) Smart Segmentation (SS) workspace of 10 prostate cancer patients for four regions of interest; such as, bladder, rectum, femoral head left, and femoral head right. The geometric and dosimetric deviation between SS and MS contours have been quantified in the form of different parameters. The organ-wise correlation between different validation parameters was addressed.
Results
The organ-wise correlation analysis showed the good and consistent correlation between different geometric validation parameters for the bladder. The hypothesis test for checking compliance of different parameters with AAPM 132 tolerance was addressed and validated between MS and SS bladder with p-value = 0.01 and 0.05. There was no significant dosimetric difference between the dose–volume histogram (DVH) estimated for the SS bladder and standard DVH constraints protocol (as per the TMH PRIME trial) with p-value = 0.01 and 0.05. The difference between DVH estimated for MS and SS bladder was also not significant, with p-value = 0.05.
Conclusion
This study shows that “well correlated validation parameters infer correctly about the matching or coincidence between auto and manually segmented contours,” and the bladder contouring by Smart Segmentation and plan optimization can achieve acceptable DVH constraints.
1 INTRODUCTION
In radiotherapy (RT), imaging and image segmentation are the most essential and important parts of the treatment protocol to delineate the treatment target and the normal structures. The different regions of interest (ROIs; including targets, normal tissues) are routinely delineated by the radiologists and oncologists with the help of diagnostic imaging and pathological remarks. The segmented images are used for treatment planning in the treatment planning system (TPS). Hence, segmentation plays a critical role in treatment outcomes. With the rapid advancement in image-guided RT and adaptive RT, a fast and accurate segmentation is a decisive part of the treatment outcome.1 Two different methods of delineation are considered; such as, manual (gold standard) and automatic through software. These two methods have different advantages and disadvantages. For the manual method, the probability of missing important ROIs is much less as the ROIs are segmented and checked at every slice by expert professionals. However, it consumes more time and is prone to intra- and interobserver variations. In other ways, the auto-segmentation may significantly decrease the delineation workload in a high patient load scenario. The quality of segmentation encompasses spatial accuracy and dose calculation accuracy. The necessity for high-throughput image segmentation machinery can be achieved only by using automated methods. Smart segmentation (SS) is a knowledge-based segmentation, which allows to do automated segmentation, using case-based segmentation from an expert case library containing cases provided by Varian or added by the user. Delpon et al. studied the different perspectives of five atlas-based auto-contouring algorithms in prostate cancer patients and compared them with contours delineated by the radiation oncologist, and suggested that the comparison of these algorithms was very efficient for high-contrast organs.2 W. Jeffrey Zabel et al. compared a standard manual contouring workflow with two auto-contouring workflows (i.e. atlas and deep learning) for contouring the bladder and rectum in patients with prostate cancer, and concluded that deep-learning auto-contouring for bladder and rectum contour delineation decreases contouring time without any negative effect on ROI editing times.3 Jeremiah Hwee et al. performed an evaluation of the accuracy, reliability, and potential time-savings by using automated atlas-based segmentation, and found good time-saving in the case of OARs (i.e. bladder, rectum, femoral head left [FHL], and right [FHR]) contouring, but suggested improvement for the prostate bed and penile bulb.4 All these studies validated different contours of ROIs by considering average parameters, such as the Dice similarity coefficient (DSC) and mean surface distance to quantify the discrepancies.
Therefore, the main purpose of the present study was to quantify the deviation between auto-segmented SS contours and manually segmented (MS) contours with five geometrical parameters; such as, DSC, Hausdorff distance (HD), centroid of planner contour, distance to agreement-% (DTA-%), center of mass (COM), and their organ-wise correlation between each other. Moreover, the parameters have been quantified for each and every slice of different organs to build more confidence on the validation. The dosimetric differences and compliance with institutional dose–volume histogram (DVH) protocol (Tata Memorial Hospital [TMH] prime trial5) have been estimated between MS and SS bladder.
2 METHODS
- DSC
- HD
- Centroid distance of planner contour (Δdcentroid)
- Center of mass distance (ΔdCOM)
- DTA-%
- Dosimetric analysis
The first five parameters can be classified as the geometric validation parameters, as they are associated with geometric discrepancies and the last one provides the dosimetric discrepancies (for more details see Supporting Information).7-10
2.1 Workflow
- A segmentation library of prostate cancer cases was created by selecting patients retrospectively from already treated patients at TMH, Mumbai, for making different contours in SS by Varian.
- The 10 prostate cancer patients were retrospectively and randomly selected (which are not included in the segmentation library) for this study. Additionally, four ROIs were selected for this work; such as, the bladder, rectum, FHL, and right.
- For metric, like DSC, the volume of each type of ROI contour (MS and SS) and their intersection (created by the Boolean operator at the contouring tab) were taken separately from Eclipse TPS 13.5. The volume DSC was computed by using Equation (1) (see Supporting Information). The number of slices segmented for one type of ROI by SS was not the same as MS contours of same type ROI. Therefore, the number of slices, where MS and SS contours (of same ROI) are present were counted separately, and the number of slices where they coexisted were also counted to calculate the slice number DSC by Equation (2) (see Supporting Information). Combined DSC was computed by multiplying the volume and slice number DSC.
- The parameter, like ΔdCOM, was computed from the COM of each 3-D ROI. For that, the external beam radiotherapy plan (in Eclipse TPS 13.5) was created making each ROI (for both MS and SS) as the target separately. The field iso-center (automatically generated by TPS) of the plan was the geometric center; that is, the COM of that target ROI. Then, the ΔdCOM of each MS and SS ROI contour was determined by Equation (5) (see Supporting Information).
- The parameters, such as HD and Δdcentroid, DTA-% were computed by Matlab 2020a coding. The structure-set containing MS and SS contours of four type ROIs was exported from TPS in DICOM file format. The Matlab 2020a version was used to analyze the DICOM data. The Matlab code was programmed to extract the coordinates (x, y, z) of each planner contour of different ROIs from the DICOM file format. In the case of parameters obtained from Matlab coding, there are two types of averaging; such as, slice average of the parameter value (the average of the parameter value over each and every contour point of a single slice is planner averaging) and average parameter value (the average of the parameter value over all slices of ROIs is 3-D averaging).
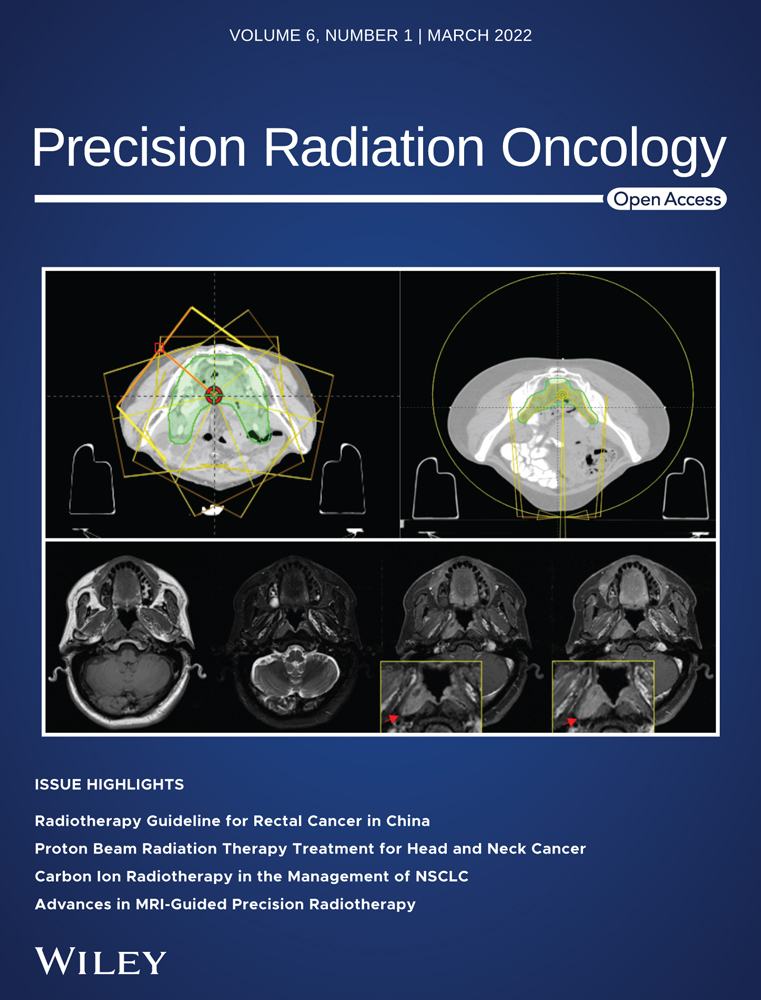
- Phantom study: The coordinate extraction coding was validated by the following method.
- The cylindrical-shaped ROIs named as planning target volume (PTV)-1 (radius 20 mm) and PTV-2 (radius 40 mm) were segmented on 10 consecutive computed tomography slices of computed tomography data of head–body phantom. The copy contour of PTV-1 was created and named as PTV-3 (radius 20 mm).
- The structure set was exported to DICOM file format, and the coordinates of that ROIs were extracted and plotted in Figure 1. The verification of extraction coding is shown in Table 1.
- The extracted contours coordinates are with respect to DICOM origin of structure set. The extensive Matlab coding for computing HD, Δdcentroid, and DTA-% from coordinates was programmed using Matlab 2020a. This coding was also verified by computing the same parameters from the aforementioned ROIs (such as PTV-1, 2, and 3). The computed data are shown in Table 1.
- The validation parameters for four different organs (i.e. bladder, rectum, FHL, and FHR) were computed and are shown in Tables 2 and 3.
- The ROI-wise correlation was found between different metrics or validation parameters. The Pearson correlation coefficient (r), coefficient of determination (R2), and p-value of correlation are shown in Tables 4 and 5. The hypothesis ‘well correlated parameters infer correctly about the matching or coincidence between auto-segmented and MS contours’ was adopted (as shown in Figure 2, Figure 3, Figure 4, and Figure 5). The above hypothesis was tested on the basis of the correlation obtained between different parameters and the significance of the correlation (p-value).
- Another hypothesis ‘parametric comparison between atlas-based SS (of Varian Eclipse 13.5) and manual segmentation bladder contour lie within the standard tolerance level as per AAPM 132′ was also adopted to test the basis of parameters’ value obtained from analysis (Table 6).6
- Dosimetric tests were performed for 10 prostate cancer patients. The DVH-based comparison of the bladder (for MS and SS contour) was studied and tabulated as per institutional stereotactic body radiotherapy (SBRT) DVH constraints in Table 7. The DVH of MS and SS bladder is plotted at Figure 6. Student's t-test was performed to test the significance of difference between the standard DVH constraints (as per TMH prime trial protocol5 for SBRT cases i.e., V14Gy < 40%, V17.5 Gy < 27%, V28Gy < 20%, V35Gy < 3%) and DVH constraints achieved in SS bladder (Table 8). Additionally, this test (Student's t-test) was also performed to check the significance of dose difference between MS and SS bladder estimated from volumetric modulated arc therapy plan with α = 0.05 level (Table 9).
| ROIs | No. slices contoured in TPS | No. slices from Matlab | Radius (mm) | Avg. HD (mm) | Avg. CD (mm) | Avg. DTA-% |
|---|---|---|---|---|---|---|
| PTV_1 | 10 | 10 | 20 | 20.41 (0.006) | 0.14 (0.18) | 0 |
| PTV_2 | 10 | 10 | 40 | |||
| PTV_1 | 10 | 10 | 20 | 0 | 0 | 100 |
| PTV_3 | 10 | 10 | 20 |
- Abbreviations: Avg. CD. average centroid distance; Avg. HD, average Hausdorff distance; DTA-%, distance to agreement-%; ROIs, regions of interest; TPS, treatment planning system.
- Note: Values in parentheses are the standard deviation of main parameters.
| ROIs | Patients | ΔdCOM (mm) | Volume DSC | Slice DSC | Combined DSC |
|---|---|---|---|---|---|
| Bladder | 1 | 2.098 | 0.927 | 0.985 | 0.913 |
| 2 | 0.55 | 0.958 | 0.960 | 0.920 | |
| 3 | 0.64 | 0.945 | 0.958 | 0.905 | |
| 4 | 1.39 | 0.926 | 0.900 | 0.833 | |
| 5 | 5.32 | 0.841 | 0.862 | 0.725 | |
| 6 | 0.88 | 0.933 | 0.935 | 0.873 | |
| 7 | 0.58 | 0.971 | 0.961 | 0.932 | |
| 8 | 3.06 | 0.939 | 0.923 | 0.867 | |
| 9 | 0.94 | 0.955 | 0.948 | 0.906 | |
| 10 | 1.09 | 1.000 | 0.965 | 0.965 | |
| FHR | 1 | 32.55 | 0.431 | 0.582 | 0.251 |
| 2 | 31.93 | 0.495 | 0.613 | 0.303 | |
| 3 | 25.92 | 0.537 | 0.691 | 0.371 | |
| 4 | 33.63 | 0.455 | 0.576 | 0.262 | |
| 5 | 33.77 | 0.451 | 0.533 | 0.241 | |
| 6 | 32.15 | 0.610 | 0.446 | 0.272 | |
| 7 | 9.18 | 0.895 | 0.661 | 0.591 | |
| 8 | 40.09 | 0.338 | 0.244 | 0.082 | |
| 9 | 30.62 | 0.600 | 0.499 | 0.300 | |
| 10 | 32.01 | 0.644 | 0.479 | 0.308 | |
| FHL | 1 | 32.94 | 0.441 | 0.604 | 0.266 |
| 2 | 32.59 | 0.487 | 0.667 | 0.325 | |
| 3 | 26.69 | 0.491 | 0.607 | 0.298 | |
| 4 | 35.72 | 0.507 | 0.533 | 0.270 | |
| 5 | 33.32 | 0.460 | 0.525 | 0.241 | |
| 6 | 34.33 | 0.552 | 0.454 | 0.250 | |
| 7 | 9.47 | 0.630 | 0.720 | 0.454 | |
| 8 | 26.09 | 0.640 | 0.484 | 0.310 | |
| 9 | 34.74 | 0.531 | 0.449 | 0.239 | |
| 10 | 35.47 | 0.571 | 0.492 | 0.281 | |
| Rectum | 1 | 13.53 | 0.596 | 0.897 | 0.534 |
| 2 | 15.34 | 0.489 | 0.688 | 0.336 | |
| 3 | 10.6 | 0.241 | 0.676 | 0.163 | |
| 4 | 14.2 | 0.588 | 0.776 | 0.456 | |
| 5 | 5.40 | 0.475 | 0.812 | 0.386 | |
| 6 | 36.17 | 0.630 | 0.278 | 0.175 | |
| 7 | 24 | 0.737 | 0.523 | 0.385 | |
| 8 | 10.38 | 0.696 | 0.492 | 0.343 | |
| 9 | 7.61 | 0.921 | 0.696 | 0.641 | |
| 10 | 15.55 | 0.681 | 0.630 | 0.429 |
- Abbreviations: ΔdCOM, center of mass distance; DSC, Dice similarity coefficient; FHL, femoral head left; FHR, femoral head right; ROIs, regions of interest.
| HD (mm) | Δdcentroid (mm) | DTA-% (mm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ROIs | Patients | Mean (SD) | Max | Min | Mean (SD) | Max | Min | Mean (SD) | Max | Min |
| Bladder | 1 | 2.50 (1.07) | 20.5 | 0 | 4.14 (3.84) | 16.16 | 0.09 | 67.36 (14.12) | 95.83 | 38.23 |
| 2 | 1.68 (0.83) | 15.17 | 0 | 1.51 (1.31) | 6.53 | 0.17 | 79.70 (15.87) | 97.56 | 40.9 | |
| 3 | 2.11 (0.94) | 14.52 | 0 | 2.15 (2.09) | 8.11 | 0.07 | 70.22 (18.54) | 93.52 | 30.7 | |
| 4 | 1.42 (1.06) | 23.1 | 0 | 1.35 (1.31) | 4.59 | 0.03 | 87.89 (12.95) | 99.35 | 50.73 | |
| 5 | 3.24 (1.82) | 31.46 | 0.00 | 7.55 (6.18) | 18.21 | 0.26 | 60.27 (21.76) | 95.77 | 19.31 | |
| 6 | 1.67 (0.75) | 10.83 | 0 | 1.19 (1.17) | 5.16 | 0.05 | 78.46 (18.8) | 97.2 | 21.42 | |
| 7 | 1.84 (1.62) | 15.3 | 0 | 1.23 (1.51) | 5.8 | 0.02 | 82.11 (24.1) | 100 | 0 | |
| 8 | 3.95 (5.47) | 48.9 | 0 | 4.05 (6.21) | 22.2 | 0.29 | 70.44 (20.5) | 98.7 | 7.14 | |
| 9 | 1.84 (1.07) | 26.6 | 0 | 2.08 (2.18) | 8.01 | 0.15 | 77.8 (16.65) | 97.53 | 30 | |
| 10 | 1.58 (0.78) | 15.9 | 0 | 1.38 (1.51) | 6.64 | 0.02 | 82.2 (14.19) | 97.33 | 52.94 | |
| FHR | 1 | 10.61(7.14) | 53.89 | 0 | 11.86 (8.89) | 22.68 | 1.36 | 40.71 (29.06) | 81.94 | 0 |
| 2 | 7.81(9.13) | 53.43 | 0.01 | 9.78 (13.09) | 32.71 | 0.76 | 51.19 (24.21) | 93.42 | 12.07 | |
| 3 | 8.51 (8.15) | 53.14 | 0 | 10.54 (10.9) | 28.88 | 0.68 | 48.17 (23.93) | 87.5 | 0 | |
| 4 | 9.26 (8.37) | 57.16 | 0.02 | 12.13 (10.77) | 30.73 | 1.72 | 55.15 (9.54) | 73.8 | 39.3 | |
| 5 | 7.91 (7.88) | 50.87 | 0 | 7.26 (9.61) | 26.51 | 0.46 | 45.45 (33.55) | 92.85 | 0 | |
| 6 | 9.15 (7.83) | 53.6 | 0.01 | 10.54 (11.03) | 31.2 | 0.933 | 47.95 (30.95) | 83.78 | 0 | |
| 7 | 7.74 (5.8) | 44.07 | 0 | 9.39 (6.5) | 22.82 | 2.51 | 43.52 (9.01) | 57.8 | 17.8 | |
| 8 | 6.64 (4.23) | 18.51 | 0 | 1.99 (1.67) | 4.55 | 0.31 | 19.09 (27.7) | 73.8 | 0 | |
| 9 | 10.05 (6.18) | 52.83 | 0.02 | 12.27 (9.94) | 32.45 | 2.4 | 32.6 (22.9) | 66.21 | 0 | |
| 10 | 10.82 (9.7) | 64.97 | 0 | 10.05 (10.38) | 24.28 | 1.06 | 28.13 (29.52) | 87.5 | 0 | |
| FHL | 1 | 11.46 (8.64) | 59.08 | 0.01 | 14.21 (11.20) | 33.91 | 0.58 | 49.62 (33.56) | 86.11 | 0 |
| 2 | 9.65 (9.41) | 57.31 | 0 | 11.9 (13.10) | 32.68 | 1.27 | 31.56 (12.81) | 61.11 | 13.46 | |
| 3 | 8.47 (7.4) | 48.57 | 0.01 | 11.6 (10.13) | 28.6 | 0.41 | 58.7 (19.7) | 83.8 | 20 | |
| 4 | 9.42 (8.42) | 55.6 | 0 | 11.61 (11.19) | 29.86 | 1.42 | 49.15 (26.23) | 83.78 | 0 | |
| 5 | 7.79 (7.77) | 49.73 | 0.01 | 8.34 (9.56) | 27.97 | 0.45 | 46.91 (33.81) | 85.29 | 0.00 | |
| 6 | 8.99 (7.5) | 53.13 | 0.01 | 10.09 (10.15) | 25.5 | 0.81 | 46.74 (31.33) | 90.22 | 0 | |
| 7 | 6.43 (4.67) | 41.02 | 0 | 7.73 (6.84) | 20.84 | 1.25 | 39.4 (16.32) | 57.81 | 0 | |
| 8 | 8.19 (7.9) | 49.9 | 0.04 | 7.61 (9.7) | 27.9 | 0.42 | 40.41 (21.7) | 78.37 | 10.71 | |
| 9 | 11.21 (6.97) | 56.53 | 0 | 13.21 (10.16) | 32.86 | 2.69 | 35.64 (25.62) | 79.41 | 0 | |
| 10 | 12.38 (9.4) | 69.12 | 0.01 | 14.16 (13.57) | 30.49 | 0.32 | 44.35 (27.35) | 81.71 | 0 | |
| Rectum | 1 | 4.49 (2.57) | 17.13 | 0.01 | 6.92 (4.75) | 14.73 | 0.47 | 43.74 (23.6) | 90.91 | 14.71 |
| 2 | 5.31 (4.55) | 24.28 | 0 | 4.81 (4.81) | 14.76 | 0.11 | 48.94 (34.30) | 100 | 0 | |
| 3 | 6.18 (2.21) | 23.37 | 0.02 | 6.41 (3.71) | 14.1 | 0.88 | 39.6 (20.9) | 77.77 | 0 | |
| 4 | 3.34 (1.77) | 12.98 | 0 | 4.77 (3.29) | 10.17 | 0.42 | 45.4 (27.01) | 95.23 | 13.33 | |
| 5 | 7.38 (6.01) | 30.45 | 0.02 | 9.02 (6.74) | 22.72 | 1.19 | 39.13 (25.51) | 88.88 | 0.00 | |
| 6 | 5.78 (3.6) | 31.56 | 0 | 6.5 (4.8) | 18.43 | 0.66 | 43.8 (24.53) | 75 | 0 | |
| 7 | 4.69 (0.99) | 15.09 | 0 | 4.57 (2.41) | 8.21 | 1.08 | 23.03 (11.1) | 42.3 | 4.16 | |
| 8 | 5.72 (5.26) | 30.17 | 0 | 6.77 (7.47) | 24.11 | 0.25 | 38.25 (25.13) | 84.21 | 0 | |
| 9 | 7.32 (5.23) | 27.97 | 0 | 10.06 (7.07) | 24.75 | 1.92 | 40.25 (24.7) | 73.44 | 0 | |
| 10 | 3.28 (0.99) | 10.48 | 0.01 | 4.47 (2.07) | 7.84 | 0.7 | 40.8 (17.17) | 95.83 | 16.6 | |
- Δdcentroid, centroid distance of planner contour; DTA, distance to agreement; FHL, femoral head left; FHR, femoral head right; ROIs, regions of interest.
| Slice Avg. HD vs. Slice Avg. CD | Slice Avg. HD vs, Slice Avg. DTA-% | Slice Avg. CD vs. Slice Avg. DTA-% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ROIs | Patient | r | R2 | p | r | R2 | p | r | R2 | p |
| Bladder | 1 | 0.750 | 0.563 | 7.57E–07 | –0.783 | 0.613 | 1.18E–07 | -0.814 | 0.662 | 1.47E–08 |
| 2 | 0.732 | 0.536 | 3.94E–07 | –0.953 | 0.908 | 3.64E–19 | –0.681 | 0.464 | 4.80E–06 | |
| 3 | 0.810 | 0.657 | 6.37E–09 | –0.956 | 0.914 | 1.28E–18 | –0.777 | 0.603 | 6.72E–08 | |
| 4 | 0.851 | 0.724 | 7.60E–06 | –0.858 | 0.736 | 5.22E–06 | –0.842 | 0.708 | 1.20E–05 | |
| 5 | 0.815 | 0.664 | 7.16E–07 | –0.911 | 0.831 | 2.40E–10 | –0.655 | 0.429 | 3.84E–04 | |
| 6 | 0.857 | 0.735 | 6.92E–07 | –0.974 | 0.949 | 1.06E–13 | –0.861 | 0.741 | 5.41E–07 | |
| 7 | 0.843 | 0.709 | 7.78E–10 | –0.947 | 0.897 | 7.39E–17 | –0.734 | 0.538 | 1.19E–06 | |
| 8 | 0.981 | 0.962 | 3.77E–22 | –0.580 | 0.335 | 6.00E–04 | –0.523 | 0.273 | 2.50E–03 | |
| 9 | 0.812 | 0.659 | 1.69E–08 | –0.830 | 0.688 | 4.36E–09 | –0.780 | 0.607 | 1.46E–07 | |
| 10 | 0.826 | 0.682 | 1.86E–08 | –0.897 | 0.804 | 1.94E–09 | –0.688 | 0.473 | 2.61E–07 | |
| FHR | 1 | 0.893 | 0.798 | 3.19E–06 | –0.250 | 0.063 | 3.50E–01 | 0.127 | 0.016 | 6.39E–01 |
| 2 | 0.984 | 0.968 | 3.67E–14 | –0.759 | 0.576 | 1.64E–04 | –0.712 | 0.506 | 6.35E–04 | |
| 3 | 0.956 | 0.913 | 1.84E–10 | –0.322 | 0.104 | 1.78E–01 | –0.333 | 0.111 | 1.63E–01 | |
| 4 | 0.983 | 0.966 | 6.69E–14 | –0.142 | 0.020 | 5.63E–01 | –0.125 | 0.016 | 6.11E–01 | |
| 5 | 0.940 | 0.884 | 6.31E–08 | –0.481 | 0.231 | 5.93E–02 | –0.234 | 0.055 | 3.83E–01 | |
| 6 | 0.939 | 0.881 | 7.88E–09 | –0.083 | 0.007 | 7.44E–01 | 0.225 | 0.051 | 3.68E–01 | |
| 7 | 0.976 | 0.952 | 2.36E–11 | –0.504 | 0.254 | 3.90E–02 | –0.409 | 0.167 | 1.02E–01 | |
| 8 | 0.579 | 0.335 | 6.18E–02 | –0.754 | 0.568 | 7.30E–03 | –0.238 | 0.057 | 4.80E–01 | |
| 9 | 0.902 | 0.813 | 3.10E–07 | 0.188 | 0.035 | 4.54E–01 | 0.553 | 0.306 | 1.70E–02 | |
| 10 | 0.944 | 0.891 | 1.28E–09 | –0.580 | 0.336 | 9.20E–03 | –0.423 | 0.178 | 7.14E–02 | |
| FHL | 1 | 0.922 | 0.850 | 3.91E–07 | –0.271 | 0.073 | 3.11E–01 | 0.062 | 0.004 | 8.18E–01 |
| 2 | 0.968 | 0.937 | 1.15E–11 | –0.031 | 0.001 | 8.98E–01 | –0.148 | 0.022 | 5.46E–01 | |
| 3 | 0.979 | 0.958 | 9.29E–12 | –0.480 | 0.231 | 5.10E–02 | –0.396 | 0.157 | 1.15E–01 | |
| 4 | 0.966 | 0.934 | 1.23E–09 | –0.415 | 0.172 | 1.10E–01 | –0.191 | 0.036 | 4.79E–01 | |
| 5 | 0.952 | 0.907 | 1.32E–08 | –0.491 | 0.241 | 5.37E–02 | –0.314 | 0.099 | 2.36E–01 | |
| 6 | 0.916 | 0.839 | 6.14E–07 | –0.316 | 0.099 | 2.32E–01 | 0.049 | 0.002 | 8.57E–01 | |
| 7 | 0.928 | 0.862 | 7.65E–08 | –0.275 | 0.075 | 2.85E–01 | –0.004 | 0.000 | 9.87E–01 | |
| 8 | 0.980 | 0.959 | 3.81E–11 | –0.417 | 0.173 | 1.07E–01 | –0.284 | 0.081 | 2.86E–01 | |
| 9 | 0.876 | 0.767 | 3.97E–06 | 0.176 | 0.031 | 4.98E–01 | 0.564 | 0.317 | 1.84E–02 | |
| 10 | 0.941 | 0.885 | 6.00E–09 | –0.161 | 0.026 | 5.22E–01 | 0.104 | 0.011 | 6.81E–01 | |
| Rectum | 1 | 0.903 | 0.816 | 3.58E–15 | –0.739 | 0.546 | 7.66E–08 | –0.836 | 0.699 | 3.47E–11 |
| 2 | 0.920 | 0.847 | 1.34E–09 | –0.353 | 0.124 | 1.07E–01 | –0.263 | 0.069 | 2.36E–01 | |
| 3 | 0.887 | 0.787 | 7.51E–09 | 0.153 | 0.023 | 4.76E–01 | 0.267 | 0.071 | 2.08E–01 | |
| 4 | 0.961 | 0.923 | 7.65E–15 | –0.885 | 0.783 | 1.99E–09 | –0.881 | 0.776 | 2.82E–09 | |
| 5 | 0.977 | 0.955 | 4.38E–19 | –0.787 | 0.619 | 6.82E–07 | –0.852 | 0.726 | 8.88E–09 | |
| 6 | 0.785 | 0.615 | 9.24E–06 | –0.669 | 0.447 | 4.80E–04 | –0.417 | 0.173 | 4.70E–02 | |
| 7 | 0.398 | 0.158 | 3.59E–02 | –0.355 | 0.126 | 6.36E–02 | –0.035 | 0.001 | 8.58E–01 | |
| 8 | 0.972 | 0.945 | 2.14E–15 | –0.786 | 0.618 | 5.20E–06 | –0.760 | 0.577 | 1.66E–05 | |
| 9 | 0.973 | 0.946 | 9.55E–19 | –0.831 | 0.69 | 2.44E–08 | –0.889 | 0.789 | 1.23E–10 | |
| 10 | 0.727 | 0.528 | 2.46E–06 | –0.776 | 0.602 | 1.78E–07 | –0.496 | 0.245 | 0.0039 | |
- Avg. CD. average centroid distance; Avg. HD, average Hausdorff distance; DTA-%, distance to agreement-%; ROIs, regions of interest; Slice-Avg. HD, average over every slice of regions of interest; TPS, treatment planning system.
| ΔdCOM (mm) versus Combined DSC | ΔdCOM (mm) versus Avg. HD (mm) | ΔdCOM (mm) versus Avg. DTA-% | ΔdCOM (mm) versus Avg. CD (mm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ROIs | r | R2 | p | r | R2 | p | r | R2 | P | r | R2 | p |
| Bladder | −0.821 | 0.674 | 4E–03 | 0.780 | 0.608 | 8E–03 | −0.741 | 0.549 | 1E–02 | 0.955 | 0.911 | 2E–05 |
| FHR | −0.972 | 0.946 | 2E–06 | 0.079 | 0.006 | 8E–01 | −0.280 | 0.079 | 4E–01 | −0.291 | 0.084 | 4E–01 |
| FHL | −0.918 | 0.844 | 2E–04 | 0.705 | 0.497 | 2E–02 | 0.101 | 0.010 | 8E–01 | 0.599 | 0.359 | 7E–02 |
| Rectum | −0.462 | 0.213 | 2E–01 | −0.299 | 0.090 | 4E–01 | −0.114 | 0.013 | 8E–01 | −0.451 | 0.204 | 2E–01 |
- ΔdCOM, center of mass distance; Avg. HD, average Hausdorff distance; DSC, Dice similarity coefficient; FHL, femoral head left; FHR, femoral head right; ROIs, regions of interest.
| Parameters | Avg. HD (mm) | Δdcentroid (mm) | ΔdCOM (mm) | Combined DSC |
|---|---|---|---|---|
| Sample mean | 2.18 | 2.66 | 1.65 | 0.88 |
| Sample SD | 0.82 | 2.04 | 1.51 | 0.07 |
| Population mean | 3 | 3 | 3 | 0.9 |
| t-value | −3.15 | −0.52 | −2.82 | −0.76 |
| Null hypothesis(H0) | μ ≤ 3 | μ ≤ 3 | μ ≤ 3 | μ ≥ 0.9 |
| Alternate hypothesis (H1) | μ > 3 | μ > 3 | μ > 3 | μ < 0.9 |
| p-value | 0.99 | 0.69 | 0.99 | 0.23 |
| α = 0.05 | Accept H0 | Accept H0 | Accept H0 | Accept H0 |
| α = 0.01 | Accept H0 | Accept H0 | Accept H0 | Accept H0 |
- Δdcentroid, centroid distance of planner contour; ΔdCOM, center of mass distance; Avg. HD, average Hausdorff distance; DSC, Dice similarity coefficient;
| Difference between DVH constraints archived for MS and SS bladder (as per TMH prime trail protocol) | Difference between doses achieved for MS and SS bladder | |||||||
|---|---|---|---|---|---|---|---|---|
| Patient | Prescription (cGy/#) | V14 Gy (%) | V17.5 Gy (%) | V28 Gy (%) | V35 Gy (%) | Max (cGy) | Min (cGy) | Mean (cGy) |
| 1 | 3625/5# (SBRT) | 4 | 3 | 2.5 | 1.8 | 18 | 0.8 | 110 |
| 2 | 3625/5# (SBRT) | 0 | 0 | 0 | 0 | 0 | 0 | 6 |
| 3 | 3625/5# (SBRT) | 0 | 0 | 0 | 0 | −176.2 | 5.2 | −12.2 |
| 4 | 3625/5# (SBRT) | 3.3 | 3.37 | 0.64 | −0.9 | −24 | −0.5 | 69 |
| 5 | 3625/5# (SBRT) | 0 | −0.5 | −1.16 | −1.25 | −46 | 5.4 | 17.2 |
| 6 | 3625/5# (SBRT) | −2.17 | −2.18 | −2.11 | 2.07 | −2.8 | −0.8 | −72 |
| 7 | 3625/5# (SBRT) | 1.46 | 1.48 | 1.4 | 1.07 | 28.2 | 1.1 | 49.6 |
| 8 | 3625/5# (SBRT) | 5.75 | 5.91 | 3.11 | 1.9 | 4.1 | 2 | 165.9 |
| 9 | 3625/5# (SBRT) | 0.69 | 0.66 | −0.01 | 0.39 | 0 | 0.2 | 23.2 |
| 10 | 3625/5# (SBRT) | 0 | −1.14 | −1.44 | −1.14 | −102.7 | 0 | −27.9 |
- DVH, dose–volume histogram; MS, manually segmented; SBRT, stereotactic body radiotherapy; SS, smart segmentation.
| Parameters | V14 Gy (%) | V17.5 Gy (%) | V28 Gy (%) | V35 Gy (%) |
|---|---|---|---|---|
| Sample average | 14.19 | 10.50 | 4.70 | 2.02 |
| Sample SD | 9.63 | 6.31 | 2.66 | 1.50 |
| Population mean (μ) | 40 | 27 | 20 | 3 |
| t-value | −8.04 | −7.84 | −17.26 | −1.96 |
| Null hypothesis (H0) | μ ≤ 40 | μ ≤ 27 | μ ≤ 20 | μ ≤ 3 |
| Alternate hypothesis (H1) | μ > 40 | μ > 27 | μ > 20 | μ > 3 |
| P value | 0.99 | 1 | 1 | 0.957 |
| α = 0.05 | Accept H0 | Accept H0 | Accept H0 | Accept H0 |
| α = 0.01 | Accept H0 | Accept H0 | Accept H0 | Accept H0 |
| Parameters | V14 Gy (%) | V17.5 Gy (%) | V28 Gy (%) | V35 Gy (%) | Max (cGy) | Min (cGy) | Mean (cGy) |
|---|---|---|---|---|---|---|---|
| t-value | 1.75 | 1.38 | 0.55 | 0.97 | −1.49 | 1.89 | 1.50 |
| p-value (α = 0.05) | 0.11 | 0.20 | 0.59 | 0.35 | 0.16 | 0.09 | 0.16 |
3 RESULTS
3.1 Phantom study
PTV_3 is the copy contour of PTV_1, therefore, by definition, HD and centroid distance (CD) should ideally be zero and the DTA% should be 100. PTV_2 (radius 40 mm) is a concentric cylinder of PTV_1 and 3 (radius 20 mm), so for those parameters the values, ideally, are HD = 20 mm, CD = 0 mm, and average DTA-% = 0. The verification table (Table 1) data and Figure 1 shows that the computed values of different parameters are quite near to their ideal values. The values of parameters comply with the variation of much less than 2–3 mm with respect to the ideal values as recommended by AAPM 132.6 The coordinate data extraction coding also was verified by parameters, such as number of slices segmented and the radius of the ROIs. Therefore, the Matlab 2020a coding for the coordinate data extraction and computing parameters efficiently does the job.
3.2 Patient study
3.2.1 Geometric validation parameters
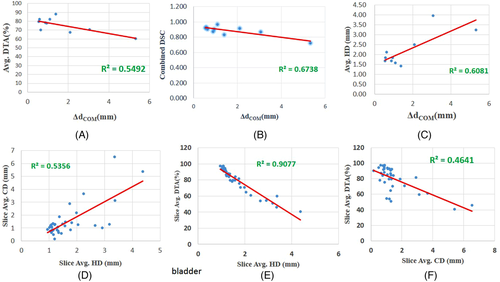
- Bladder: The combined DSC value (both slice number and volume DSC) for the bladder is close to 0.9, which is suggested by AAPM-1326 (Table 2). Now the other parameters, such as ΔdCOM and Δdcentroid, show that the average value over 10 patients for the bladder is also less than or equal to the voxel dimension (∼2–3 mm) (Tables 2 and 3). The average HD value over 10 patients is 2.18 mm, which is within the range of mean distance to agreement tolerance (2–3 mm). The values of average DTA-% (over all slices) for every patient are also higher in percentage (Table 3). The value of maximum DTA-% for every patient is >90%.
- Rectum: The combined DSC values (both slice number and volume DSC) are not proximal to the compliance of AAPM-132. The other parameters, such as ΔdCOM, average HD (over all slices), average CD (Δdcentroid), and the average DTA-%, show large discrepancies from the AAPM 132 tolerances.
- FHR and FHL: The values of different validation parameters also show large deviations from compliance values, such as the rectum.
3.2.2 Correlation analysis between geometric validation parameters
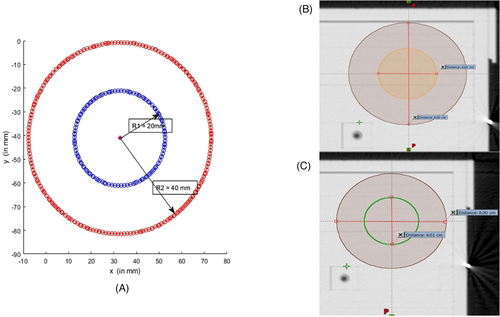
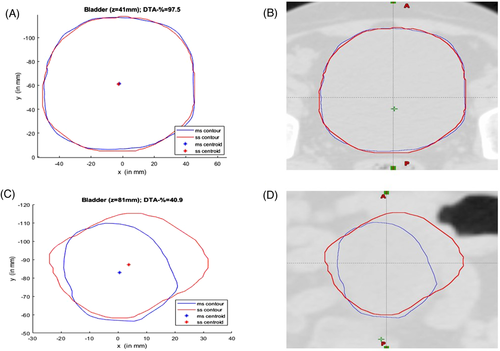
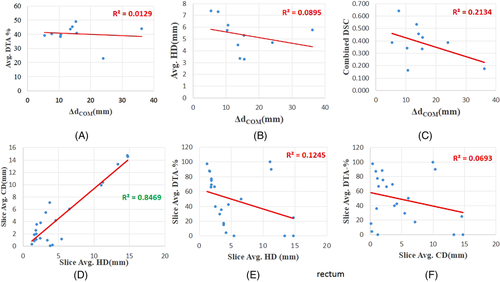
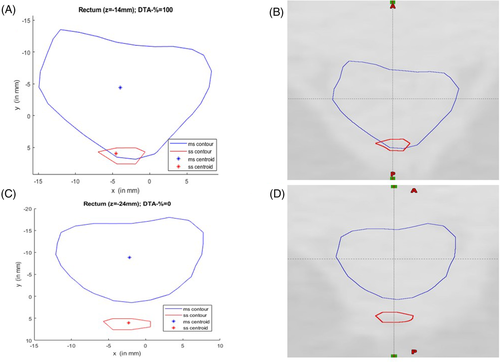
- Bladder: It is quite obvious that the values of Pearson's r, R2 (coefficient of determination) of the mutual correlation of slice average HD, slice average CD (Δdcentroid), and slice average DTA-% for the bladder are on the higher side. Therefore, they are well correlated (Table 4). The p-value confirms the significance of their correlation with significance levels of 0.01 and 0.05 (Table 4). The intercorrelation between different average parameters estimated are quite good for the bladder (Table 5). The correlation plots of all the parameters of the bladder show clear conformation as well (Figure 2). The slice of the maximum and minimum DTA-% for patient 2 are shown in Figure 3.
- Rectum: The slice average HD and slice average CD are strongly correlated with p-value < 0.01 and 0.05. The intercorrelation between slice average HD slice average DTA-% is also quite good, except in the case of patients 2 and 3. The intercorrelation between slice average CD versus slice average DTA-% shows higher R2 values, except for patients 2 and 3. But the intercorrelation between ΔdCOM versus combined DSC (r = –0.462, R2 = 0.213) and ΔdCOM versus average CD (r = –0.451, R2 = 0.204) are weak. There is no correlation between other parameters (such as ΔdCOM vs. average HD and ΔdCOM vs. average DTA-%) for the rectum.
- FHR and FHL: In the case of FHR, for every patient the slice average HD and slice average CD are strongly correlated, yet in the case of some patients, there is less or no correlation for other slice average parameters (slice average HD vs. slice average DTA-% and slice average CD vs. slice average DTA-%). The intercorrelation between ΔdCOM versus combined DSC (r = −0.972, R2 = 0.946) is good, but there is no correlation between other parameters (such as ΔdCOM vs. average CD, ΔdCOM vs. average HD and ΔdCOM vs. average DTA-%). In the case of FHL, the same is also observed from correlation analysis, except there is a weak correlation between average HD and ΔdCOM.
The significance of an organ-wise correlation study of different validation parameters can be described by using the case of patient 2.
For patient 2, the r (R2) value of the correlation between slice average HD versus slice average CD, slice average HD versus slice average DTA-%, and slice average CD versus slice average DTA-% are 0.732 (0.536), −0.953 (0.908), and −0.681 (0.464), respectively, for the bladder, and the p-values of the correlation show better significance with p-value < 0.01 or 0.05 (the null hypothesis has been adopted, as all parameters are independent). For the bladder, the r (R2) value for the correlation between ΔdCOM versus combined DSC, ΔdCOM versus average HD, ΔdCOM versus average DTA-%, ΔdCOM versus average CD are −0.821 (0.674), 0.780 (0.608), −0.741 (0.549) and 0.955 (0.911), respectively (Table 5). The bladder slice of maximum DTA-% (of patient 2) shows the true coincidence of MS and SS contours (Figure 3). The bladder slice of minimum DTA-% (of patient 2) also shows less coincidence. However, in the case of the rectum, slice average HD versus slice average CD are strongly correlated (r = 0.920, R2 = 0.847) with p < 0.01 significance level, but slice average HD versus slice average DTA-% (r = −0.353, R2 = 0.124) and slice average CD versus slice average DTA-% (r = −0.263, R2 = 0.069) are not correlated statistically with p < 0.01 or 0.05 significance levels (Table 4). The r (R2) value for the correlation between ΔdCOM versus combined DSC (Table 5) is −0.462 (0.213; not strongly correlated). The same can be concluded for the correlation between other parameters also (Table 5). Figure 4 confirms the absence of a good correlation between some parameters for the rectum. As a result, it can be seen from Figure 5 that the maximum DTA-% is 100 in the case the rectum, but it does not mean the ideal coincidence of MS and SS contours. The same can also be observed for FHL and FHR.
From this above case, it can be well understood that the better inference of coincidence between MS and SS contours is directly related to an organ-wise correlation between all the validation parameters. The present study also suggests that the one validation parameter cannot infer correctly about the coincidence of contours. The correct inference about the coincidence of MS and SS contours can be only made if, and only if, good correlation between different validation parameters of any organ exists.
It can be seen that the validation parameters for the bladder show a good and consistent correlation. Hence, the second hypothesis ‘parametric comparison between SS (of Varian Eclipse 13.5) and manual segmentation bladder contour lie within the standard tolerance level as per AAPM 1326’ has been adopted to test. In the present study, the hypothesis tested with both α = 0.05 and 0.01 significance levels. The 10 patients were sampled. The test has performed for all the computed parameters. The expected population mean (μ) of parameters were assumed the tolerance value of metrics to evaluate image registration, as prescribed by AAPM-132.6 As per AAPM 132, (a) the mean surface distance between two contours on registered images (here i.e. average HD) should be within the contouring uncertainty of the structure or maximum voxel dimension (∼2–3 mm), and (b) the volumetric overlap of two contours on registered images (i.e. DSC) should be 0.8–0.9. Hence, the population mean (μ) for average HD, ΔdCOM, and average Δdcentroid were taken as 3 mm. The population mean value for DSC was assumed as 0.9. The average value and standard deviation were calculated for the sample of 10 patients. The information about the hypothesis test is shown in Table 6. It was assumed that the sample follows Student's t-distribution, as its degree of freedom is 9. The null hypothesis (H0) for every parameter is shown in Table 6. In the case of all the parameters, such as average HD, average Δdcentroid, ΔdCOM, and combined DSC, the hypothesis test accepts H0 with α = 0.01 and 0.05 significance levels (Table 6).
3.2.3 Dosimetric analysis
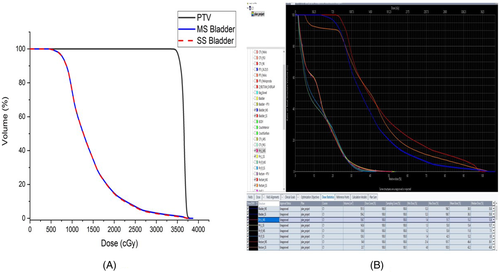
The difference between MS and SS bladder, as per the DVH reporting protocol of TMH, are shown in Table 7. Dose differences (for maximum, minimum, and mean) are shown in the same table. The relative volume difference (as per TMH dose reporting protocol for SBRT) between the MS and SS bladder is much less. The DVH of MS and SS bladder for SBRT cases almost coincide with each other. The DVH for MS and SS bladder (for patient two) is shown in Figure 6. The maximum dose difference between MS and SS bladder is reported for patient 3 (maximum difference is 176 cGy). The minimum dose difference is much less. The mean dose difference is higher only for patient 1. Student's t-test has performed and tabulated to check the significance of difference between the dose estimated for MS and SS bladder with α = 0.05 (Table 9). The null hypothesis was assumed as “there is no difference between doses of MS and SS bladder.” This test suggests that the difference is not significant, with p-value > 0.05. The hypothesis test was performed to check the significance of the difference between standard DVH dose constraints (as per TMH prime trial5) and the SS bladder for SBRT cases (Table 8). The Student's t-distribution was assumed to estimate the p-value. The null hypothesis was assumed as the compliance of DVH constraints. For all 10 SBRT cases, the result of the test inferred to accept the null hypothesis with both α = 0.01 and 0.05 level of significance.
4 DISCUSSION
From the phantom study, it can be concluded that the Matlab 2020a coding for the coordinate data extraction and computing parameters efficiently did the job. By investigating the organ-wise correlation of different geometrical validation parameters, there exists a good and consistent correlation for the bladder. Henceforth, from the organ-wise correlation analysis between geometric validation parameters, it can be also inferred the hypothesis “well correlated parameters infer correctly about the matching or coincidence between auto-segmented and MS contours” has been validated. According to the present study, the organ-wise correlation of different validation parameters plays a major role for validation of auto-segmented ROI contours. Delpon et al. reported a mean DSC value of 0.81 ± 0.13 for the bladder for ABAS, which is quite similar to the combined DSC of 0.88 ± 0.07 for SS contour of the bladder.2 In the clinical evaluation study carried out by Caria et al., the auto-contours by SS were clinically evaluated and graded by expert clinicians by their accuracy, for prostate cases, and they reported that the bladder has the most accurate and accepted auto-contours, whereas the rectum is the least accurate, as it changes its shape and position.11 As per the results of the present study, the investigation also suggests that the geometrical validation parameter for SS bladder complies with the AAPM 132 tolerances, and this has been hypothetically proven with p-value = 0.01 and 0.05. However, in the case of other ROIs, the value of geometric parameters are beyond the AAPM tolerances. The study carried out by Huyskens et al. also reported expert clinicians’ grading of the bladder, rectum, and femoral head auto-contouring, and the Smart segmentation showed 36% excellent, 42% good, 12% acceptable, and 9% unacceptable auto-contouring for the bladder; 3% excellent, 24% good, 27% acceptable, and 45% unacceptable auto-contouring for the rectum; and 12% excellent, 27% good, 6% acceptable, and 54% unacceptable auto-contouring for the femoral head, and in this study, the DSC value for bladder auto-segmentation was reported as 0.9.12 In the case of dosimetric study, it can also be reported that the auto-segmented bladder dosimetrically complies with the standard DVH constraints (TMH prime trial protocol), with 0.05 and 0.01 level of significance. Therefore, it can be concluded that the SS of Varian Eclipse 13.5 can be used to contour the bladder for prostate patients.
However, the metrics are intuitive and quantitative, but might not always reflect the clinical impact due to discrepancy. It should be emphasized that even though MS contours were considered the as references, they may not be the exact gold standard, as manual segmentations are subjected to inter- and intra-observer variation.1 However, that requires many more additional endeavors to segment for the same atlas, and it has not been pursued in this course of study. The different studies reported the interrater variability in terms of DSC being near 0.9–0.94, whereas auto-segmentation accuracy is in the range of 0.86–0.93 for the bladder.12, 13 In this present study, the value of auto-segmentation accuracy for the bladder in terms of DSC is 0.88 ± 0.07. For interpretation of the significance of the geometric discrepancies in the given results, the result should be compared with the magnitude of typical inter- and intra-observer variations.
5 CONCLUSIONS
The present study shows that both bladder contouring by Varian SS and plan optimization on this bladder can achieve the acceptable DVH constraints. The dose difference between MS and SS bladder is not statistically significant (p-value > 0.05). Yet, some of the dosimetric difference (such as maximum, minimum, and average doses) due to contour differences may be substantial. Therefore, this also requires human intervention to achieve clinically significant contours for the bladder, and acceptable plans even when automated Smart Segmentation is used. The quality of Varian Smart Segmentation for other ROIs; such as, the rectum, FHL, and FHR, is not able to achieve the significant level of compliance with the standard AAPM 1326 in the present study.
ACKNOWLEDGMENTS
Authors would like to acknowledge Dr J.P. Agarwal, Dr Anil Tibdewal, Dr V Murthy, all the Radiation Oncologists (who have segmented the patient CT images) and all the Medical Physicists (who have made the final treatment plan for the treatment and done the Dosimetric Validation QA) at Tata Memorial Hospital, Mumbai. The authors also acknowledge Varian Medical Systems.
CONFLICT OF INTERESTS
None.
AUTHORS’ CONTRIBUTION
Sudipta Mandal: Investigation, Data Collection, Formal and Statistical analysis, Matlab 2020a Coding, Writing & Editing- original draft etc. Shrikant N. Kale: Conceptualization, Supervision, Literature survey, reviewing & editing of original draft. Rajesh A. Kinhikar: Resources, Supervision.