A novel ensemble ARIMA-LSTM approach for evaluating COVID-19 cases and future outbreak preparedness
Somit Jain, Shobhit Agrawal, and Eshaan Mohapatra contributed equally to this study.
Abstract
Background
The global impact of the highly contagious COVID-19 virus has created unprecedented challenges, significantly impacting public health and economies worldwide. This research article conducts a time series analysis of COVID-19 data across various countries, including India, Brazil, Russia, and the United States, with a particular emphasis on total confirmed cases.
Methods
The proposed approach combines auto-regressive integrated moving average (ARIMA)'s ability to capture linear trends and seasonality with long short-term memory (LSTM) networks, which are designed to learn complex nonlinear dependencies in the data. This hybrid approach surpasses both individual models and existing ARIMA-artificial neural network (ANN) hybrids, which often struggle with highly nonlinear time series like COVID-19 data. By integrating ARIMA and LSTM, the model aims to achieve superior forecasting accuracy compared to baseline models, including ARIMA, Gated Recurrent Unit (GRU), LSTM, and Prophet.
Results
The hybrid ARIMA-LSTM model outperformed the benchmark models, achieving a mean absolute percentage error (MAPE) score of 2.4%. Among the benchmark models, GRU performed the best with a MAPE score of 2.9%, followed by LSTM with a score of 3.6%.
Conclusions
The proposed ARIMA-LSTM hybrid model outperforms ARIMA, GRU, LSTM, Prophet, and the ARIMA-ANN hybrid model when evaluating using metrics like MAPE, symmetric mean absolute percentage error, and median absolute percentage error across all countries analyzed. These findings have the potential to significantly improve preparedness and response efforts by public health authorities, allowing for more efficient resource allocation and targeted interventions.
Abbreviations
-
- ANN
-
- artificial neural network
-
- ARIMA
-
- auto-regressive integrated moving average
-
- CNN
-
- convolutional neural network
-
- GRU
-
- Gated Recurrent Unit
-
- LSTM
-
- long short-term memory
-
- MAPE
-
- mean absolute percentage error
-
- MDAPE
-
- median absolute percentage error
-
- RNN
-
- recurrent neural network
-
- SMAPE
-
- symmetric mean absolute percentage error
1 INTRODUCTION
The emergence of COVID-19 in late 2019 sparked a global pandemic, posing unprecedented challenges to public health and economies worldwide. India, with its vast population and diverse socioeconomic landscape, has become a crucial case study for understanding the virus's dynamics. Previous studies have explored the potential of deep learning methodologies for COVID-19 forecasting, highlighting their effectiveness in capturing complex data relationships. For instance, Shastri et al. [1] compared the performance of different deep learning models in predicting caseloads for India and the United States, while Zeroual et al. [2] emphasized the benefits of deep learning algorithms in capturing the nonlinear relationships inherent in COVID-19 data.
However, traditional statistical models have also proven valuable in time series forecasting, demonstrating competitive performance in various domains. Ang et al. [3] offered a thorough review of deep learning approaches for time series data, acknowledging their strengths while recognizing the continued relevance of traditional techniques. Azad et al. [4] successfully implemented a hybrid auto-regressive integrated moving average (ARIMA)-artificial neural network (ANN) model for water level prediction, showcasing the potential of combining established statistical approaches with the flexibility of ANNs. Similarly, Swaraj et al. [5] illustrated the effectiveness of ARIMA-based stacking models in predicting COVID-19 cases in India, emphasizing the value of these well-understood methods in pandemic forecasting. Additionally, Paidipati and Banik [6] demonstrated the competitiveness of ARIMA models compared to long short-term memory (LSTM)-NNs in rice cultivation forecasting, suggesting their applicability to diverse time series problems.
This research focuses on analyzing COVID-19 temporal patterns in India and introduces an ARIMA-LSTM approach to enhance predictive accuracy. This study aims to improve forecasting precision for targeted interventions and resource allocation at the state level. By assessing predictive accuracy and identifying key influencing factors, the research seeks to deepen the understanding of the pandemic's impact on diverse Indian populations, while offering insights for broader time series analysis beyond COVID-19.
The study aims to enhance predictive accuracy by merging traditional statistical models such as ARIMA with modern deep learning approaches like LSTM, specifically focusing on COVID-19 data in India. By developing a novel hybrid model tailored to the unique dynamics of COVID-19, the research seeks to provide valuable insights to public health authorities and policymakers, facilitating better preparedness and response efforts. While hybrid time series models have shown promise in forecasting real-world phenomena, their application to accurately predict COVID-19 cases in India remains largely unexplored. Most existing studies rely on individual statistical models or deep learning techniques, potentially overlooking the advantages of combining these approaches.
The objectives of the study are elaborated as follows:
- (1)
Compare the performance of Gated Recurrent Unit (GRU), ARIMA, Prophet, LSTM, and the hybrid ARIMA-LSTM.
- (2)
Leverage ARIMA's ability to capture linear trends alongside LSTM's capacity to model complex, nonlinear relationships in time series data.
- (3)
Apply the hybrid ARIMA-LSTM model to data sets from diverse regions for comparative evaluation.
- (4)
If successful, this approach could be used to predict future outbreaks similar to COVID-19, enabling targeted interventions by public health authorities, and leading to more efficient resource allocation and a more resilient global health system.
Table 1 represents an analysis of existing scholarly research and literature on time series analysis.
| Reference No. | Methods | Data set | Remarks | Limitations/future work |
|---|---|---|---|---|
| [1] | Stacked LSTM, bidirectional LSTM, ConvLSTM | COVID-19 confirmed and death cases of India and the United States from various government health agencies | According to the authors, for both the countries, there will be an increase for the next 1 month in both confirmed and death cases | Study COVID-19's economic impact to guide recovery strategies. Predict future cases and verify aerosol transmission to inform countries' preparedness |
| [2] | NN-based models such as VAE, BiLSTM, RNN, LSTM, and GRU | Data sets of confirmed and recovered cases that are accessible to the public, gathered from six nations: China, the United States, Australia, Spain, Italy, and France. (by Johns Hopkins University's Center for Systems Science and Engineering) | VAE performed the best among all the models | Models don't incorporate external factors like interventions and social dynamics |
| [5] | ARIMA, NAR, hybrid ARIMA-NAR, LSTM, SIR | Confirmed cases, reported deaths, and recovered cases were taken from the official COVID-19 Data Repository of Johns Hopkins University | Proposed hybrid ARIMA model, ARIMA-NAR, performed the best | Model accuracy diminishes for longer-term forecasts (months) on larger data sets |
| [7] | LSTM | The Canadian Health Authority and Johns Hopkins University provided the COVID-19 data utilized in this study, which included the number of confirmed cases up until March 31, 2020 | Compared to other provinces, those that enforced social distancing policies before the pandemic have fewer confirmed cases | Limitation in the number of methods used to forecast, only one model LSTM was used |
| [8] | SEIR, Regression model | Indian COVID-19 data (January 30–May 10, 2020) | SEIR model outperformed Regression model | Restricted to May 2020, limiting generalizability and does not take into account the seasonality |
| [9] | LSTM, ARIMA with AIC optimized and model retraining, ARIMA with AIC optimized and simple forecasting | Confirmed and death cases from the website ourworldindata.org for a period from February 22, 2020, to April 23, 2020 | ARIMA retraining model works best for all the countries. LSTM is deviating from the actual trend | Limited timeframe of the data is used, might not capture future changes in behavior |
| [10] | ARIMA | Johns Hopkins COVID-19 data for Gulf countries | The model performed the best for Qatar | Limited to early pandemic phase, model assumptions might not hold in all scenarios |
| [11] | ARIMA, NAR | Daily confirmed COVID-19 cases from India (January 31, 2020 to April 5, 2020) | NAR model achieved lower RMSE compared to ARIMA model | Considers data from early pandemic and does not use any new hybrid method. |
| [12] | ARIMA, Simple Average, Naive method, Moving Average, Holt Linear Trend Method, Single Exponential Smoothing, Holt-Winters Method | Daily COVID-19 confirmed cases along with deaths and recoveries from WHO dashboard (January–May 2020) | Naive method performed best for predicting death cases and ARIMA model predicted increasing death cases | Machine learning methods performs better than time series methods |
| [13] | Random Forest, SVM, Linear Regression, MLP | COVID-19 data between a period of January 20, 2020 and September 18, 2020 of the United States, Germany, and the global was collected from WHO | SVM outperformed all the other models | Could have used the time series analysis using ARIMA or neural networks |
| [14] | Segmented regression and Lee Carter model | Human mortality database | YLL in women was higher than that of men | No usage of time series model or hybrid time series model with Machine learning models |
| [15] | MLP ANN with moving average filter | WHO data till May 11, 2020 | Two hidden layers, nine and four neurons for layers first and second and sigmoid tangent activation functions for the hidden layers and linear to the output layer provided the best results | Effective predictions for up to only 6 days for all cases and deaths categories in most countries |
| [16] | ANN, RNN | Spread of the COVID-19 disease throughout Indonesia from 2020 to April 2022 | RNN performed better than ANN | Discover a more effective way to boost ANN models' performance while using time series-based data sets for classification, The use of “binary cross-entropy” for the RNN model's loss parameter, as well as the construction of a more refined model by either utilizing a different activation function or adding additional nodes |
| [17] | Basic, Stacked, and Bidirectional LSTM | Daily cases in nine cities across three countries with varying climatic zones, including Sweden, India, and the United States | Univariate models were outperformed by the multivariate LSTM model | Enhance the predictive power of these models by data augmentation, generative adversarial networks, and transfer learning by utilizing some of the previous epidemiological models as a network that has already been trained |
| [18] | ARIMA, Prophet, GLMNet, Random Forest, XGBoost | COVID-19 data set taken from ourworldindata.org, considering only one variable “number of confirmed COVID-19 cases” for SAARC countries | ARIMA model works best for predicting COVID-19 cases in the aforementioned nations | The authors plan to investigate the projection methodology and apply statistical models for prediction to update the data set |
| [19] | Beesham's prediction model and Boltzmann Function-based model | Positive cases in India from a period of January 1 to October 31, 2021 | ANN-BP model was used and the previous 14-day value was used to predict covid cases | The work is done as an initial benchmark, further work can be done to predict more accurately |
| [20] | CNN-LSTM | A range of symptoms as well as basic patient data, including the date of the test, gender, age, and COVID-19 test findings for about 2.75 million people | CNN-LSTM worked better than all other models | Boosting accuracy by combining fuzzy logic frameworks with machine learning models and applying meta-learning strategies |
| [21] | Stochastic Forecasting Models—LSSVM, SIR, SEIR | Positive, negative and death cases for COVID-19 | Provides an overview of various methods | Forecasting efficiency can be impacted by several circumstances, and appropriate methodology and explicit consent are not available for all data sets |
| Supervised Machine Learning Models—SVM, Random Forest, ETS, Linear Regression, Lasso Regression | ||||
| Soft Computing—ANN, ARIMA, MLP, ELM, Neural Network Auto Regression Model (NNETAR) | ||||
| Deep Learning Models—CNN, RNN, LSTM, GRU, NARNN, Bi-LSTM | ||||
| [22] | Vanilla RNN, GRU, LSTM, and (Bi-LSTM) | Data set created—periodic and nonperiodic sequences, electric load forecasting data, traffic flow, exchange rate, solar energy | Prediction was better in robust RNNs when noise was reduced | Adaptive technique for automatically adjusting robust RNN hyper-parameters |
- Abbreviations: AIC, akaike information criteria; ANN, artificial neural network; ANN-BP, artificial neural networks-back propagation; ARIMA, auto-regressive integrated moving average; CNN, convolutional neural network; ELM, extreme learning machine; ETS, exponential smoothing; GRU, Gated Recurrent Unit; LSSVM, least square support vector machine; LSTM, long short-term memory; MLP, multilayer perceptron; NAR, nonlinear autoregressive; NARNN, nonlinear autoregression neural network; RMSE, root mean square error; RNN, recurrent neural network; SEIR, susceptible, exposed, infection and recover; SIR, susceptible, infection and recover; SVM, support vector machine; VAE, variational autoencoder; YLL, years of life lost.
Ensafi et al. [23] conducted time-series forecasting of seasonal item sales using various techniques on the Superstore Sales data set. They found that neural network models, especially Stacked LSTM, outperformed traditional methods in terms of accuracy. The study recommended further research to compare these models and evaluate forecasting techniques for additional seasonal items. Performance metrics included mean squared error (MSE) = 16515.49, root mean square error (RMSE) = 128.51, and mean absolute percentage error (MAPE) = 17.34.
Livieris et al. [24] introduced a model namely convolutional neural network (CNN)-LSTM for forecasting gold prices using data from January 2014 to April 2018 sourced from finance.yahoo.com. By combining LSTM models with convolutional layers, they improved the model's forecasting capacity. The study emphasized the need to address anomalies in gold prices during periods of global unrest in future research. Performance metrics included mean absolute error (MAE) = 0.0099, RMSE = 0.0127, accuracy = 55.26%, area under the curve (AUC) = 0.553, sensitivity = 0.553, and specificity = 0.553.
Mudassir et al. [25] utilized machine learning for Bitcoin price time-series forecasting, comparing ANN, Stacked ANN, support vector machine, and LSTM models using data from bitinfocharts.com. LSTM was the best-performing model. The study suggested incorporating hourly prices, technical indicators, and ensemble models for improved accuracy. Performance metrics included MAE = 2.20, RMSE = 3.01, and MAPE = 0.93.
Kumar et al. [26] introduced a hybrid model, beta seasonal autoregressive moving average (βSARMA)-LSTM, which combines βSARMA and LSTM networks for time-series forecasting. They utilized data sets such as Sunspot, Air Passenger, Relative Humidity of India, and Mackey Glass series. Results favored the βSARMA-LSTM model, with suggestions to explore nonlinear models beyond LSTM and use dynamic selection techniques for optimal model combinations. Reported performance metrics included median absolute error = 7.791007, symmetric mean absolute percentage error (SMAPE) = 0.298088, and mean absolute scaled error (MASE) = 0.507512.
Borges et al. [27] used LSTM and Prophet models in a two-stage approach to data from São José dos Campos municipality. They introduced a Prophet-LSTM ensemble technique that outperformed benchmarks, although the models were not validated with benchmark data sets. The reported performance metric was an MAE = 0.99.
Mostafiz et al. [28] used generative adversarial network (GAN) for data generation and region-based convolutional neural network (R-CNN) for diagnosing COVID-19 and chest infections, analyzing 6406 images from various sources. R-CNN outperformed traditional methods, supported by GAN-generated data. The study did not explore hybrid models or benchmark data sets. Reported metrics included accuracy = 99.16% and AUC = 98.36%.
Hanif et al. [29] examined time series forecasting of student enrollment using Moving Average (MA) and the Fuzzy Interval Partitioning Method on an Enrollments data set. The fuzzy interval method outperformed other tested methods, though the authors noted the need to explore the impact of interval length on forecast accuracy. Reported metrics included RMSE = 213.75, MSE = 45689.062, and mean forecast error = 1.22.
Semenoglou et al. [30] introduced the Augmented Neural Network for univariate time series forecasting and evaluated it on the M4 and Tourism data sets. They found that upsampling and time-series combinations consistently improved accuracy, while other augmentation techniques had mixed results. The study recommended exploring more neural networks and machine learning models. Reported performance metrics included MASE = 2.93.
Ahmed et al. [31] used the M3 data set to compare machine learning methods for time-series forecasting. The models comprised support vector regression, kernel regression, K-nearest neighbor regression, radial basis functions, Bayesian neural networks, multilayer perceptron (MLP), and Gaussian processes. MLP and Gaussian processes were the top performers, though the study recommended the inclusion of newer algorithms for a comprehensive comparison. Reported metric: SMAPE = 0.0384.
2 METHODS
2.1 Data set description
The COVID-19 data used in this study was sourced from the Center for Systems Science and Engineering at Johns Hopkins University, a well-established and reliable data repository [32]. The data set focuses on worldwide time series data for confirmed COVID-19 cases and includes key columns such as Province/State, Country/Region, Latitude (Lat), Longitude (Long), and specific dates recorded as independent columns. The data set originally consists of 289 rows (representing various counties and locations) and 1147 columns (representing dates and location coordinates). It covers a comprehensive timeframe of 1143 days, starting from January 22, 2020, through March 9, 2023.
2.1.1 Hardware and software
The models were operated on a PC with Windows 11, equipped with an AMD Ryzen 7 processor clocked at 2.9 GHz and 16 GB of RAM. The software used Python 3.11.1, along with several essential libraries, including NumPy (v1.23.5), Pandas (v1.5.3), matplotlib (v3.7.1), seaborn (v0.12.2), sklearn (v1.2.1), and Keras (v2.12.0).
2.1.2 Data preprocessing
The data set was mostly clean, with no null values, making preprocessing straightforward. After removing irrelevant columns, the scope was narrowed specifically to focus on COVID-19 data related to India. The data was then transformed and prepared for analysis by transposing the rows and columns for easier analysis and visualization. Before feeding the data into the model, the target variable was scaled using the Min–Max Scaler technique to normalize the data and capture better intradata relationships, minimizing biases in the predictions.
2.2 Models analyzed
Figure 1 provides an overview of the implementation of the baseline models in this study.
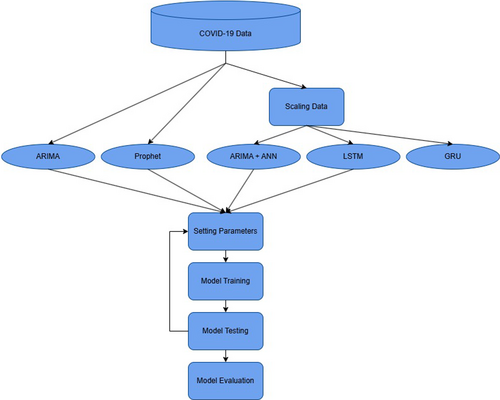
The workflow of the benchmark models resembles a data pipeline with several key stages. First, COVID-19 data is collected, followed by pre-processing to ensure data quality. Since the data values were very large, feature scaling, specifically Min–Max scaling, was implemented to standardize the data set. The data set was then divided into training, validation, and testing sets, and multiple models—such as ARIMA, Prophet, LSTM, and GRU—were trained on the data. Hyperparameter tuning on the validation/testing set optimized each model's performance, and finally, the models were evaluated for their sensitivity to the error rate.
2.2.1 Prophet
Prophet is a time series forecasting method that accounts for nonlinear trends with yearly, monthly, and daily seasonality, as well as the effects of holidays, using an additive model. It performs best on time series with several seasons of historical data and strong seasonal influences. Prophet manages anomalies well and is resilient to missing data and shifting trends [8].
2.2.2 Recurrent neural networks (RNN)
RNNs are excellent deep learning tools for time series analysis. However, RNNs struggle with long-term dependencies due to the vanishing gradient problem. Unlike traditional models that only consider the current state, RNNs use hidden layers to capture temporal information. However, the flow of information is limited, reducing performance in tasks requiring long-term memory. LSTM and GRU address this limitation, making RNNs a valuable tool for time series forecasting [1, 2].
The LSTM was designed to overcome the vanishing gradient problem that limits the performance of basic RNN. The vanishing gradient occurs when the weights barely change during training, affecting the optimizer's backpropagates [2]. LSTM solves this issue by employing a memory mechanism. The forget, input, and output gates in LSTM regulate the information flow, determining how much of the input data from the current timestep should be merged with the hidden and prior memory states. These gates then output the following memory and hidden states [3].
The GRU is another variation of RNN that addresses the vanishing gradient problem while lowering processing costs [3]. GRU merges the input and forget gates of the LSTM model into a single gate, known as the update gate. GRU has only two gates: the update controls the quantity of previously stored memory, while the reset gate manages the combination of new inputs and past memory [2].
2.2.3 Hybrid ARIMA-ANN
In hybrid ARIMA-ANN models, ARIMA handles the linear components of time series data, while ANN are used for the nonlinear components. In this model, ANN models the error sequence from the ARIMA forecast as a nonlinear function. The final prediction is a combination of the results from both the ARIMA and ANN models, which improves efficiency and performance compared to using either ARIMA or ANN alone [33].
2.3 Proposed model ARIMA-LSTM
Figure 2 illustrates the workflow of the proposed ARIMA-LSTM model.
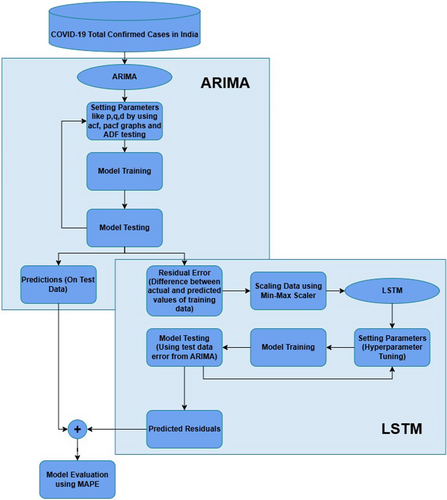
The model integrates the strengths of ARIMA and LSTM to improve time series prediction precision by leveraging both linear and nonlinear modeling capabilities. The process starts with ARIMA to capture linear trends and seasonality, involving data preprocessing, stationarity checks, and parameter selection using autocorrelation function and partial autocorrelation function analysis.
Once ARIMA parameters are determined and the model is fitted to the training data, residuals are computed. These residuals represent the variation between the ARIMA model's predictions and the actual values. To capture nonlinear patterns in the data, the residuals are fed into an LSTM neural network.
Before inputting the residuals into the LSTM, Min–Max scaling is applied for normalization. Hyperparameters of the LSTM model, such as neuron count, activation function, learning rate, and epochs, are systematically explored for optional values. Early stopping is employed during training to prevent overfitting.
After the LSTM model is trained, residuals for the test data are generated and transformed back to the original scale. Final predictions are made by combining the ARIMA model's output (for test data) and LSTM model's output (for residuals). The model's performance is evaluated using MAPE, and predictions are visualized for thorough analysis. This hybrid approach ensures a robust combination of linear and nonlinear modeling for improved accuracy.
2.3.1 Methodology adapted
The proposed ARIMA-LSTM ensemble model integrates ARIMA with LSTM to forecast COVID-19 cases more precisely. ARIMA is a statistical analysis model that use time series data to comprehend and forecast future patterns. It has three components: Auto Regressive (AR), which considers the variable's dependence on its past values; Integrated (I), which involves differencing raw observations to achieve stationarity; MA, which captures dependencies between observations and their residual errors, collectively capturing trends.
For ARIMA to function, the data set must be stationary. The Augmented Dickey-Fuller test is used to verify if the data meets this condition. If the series lacks stationarity, trends, and seasonality are removed through transformations like logarithmic functions or polynomial fittings, while differencing or decomposing handles seasonality.
ARIMA relies on three parameters—p, d, and q—that govern lag order, differencing degree, and the size of the MA window, respectively. Once these parameters are selected optimally, the model is built to make predictions.
Differenced data refers to the difference between successive values in a time series, which ensures stationarity.
The LSTM model, a type of RNN, is trained using the residuals from the ARIMA model (the difference between the actual and predicted values). The LSTM learns a function that converts historical data points into future observations. The data are transformed into sequences, and the model uses these sequences to predict future values. It requires a list of features (X) and their related labels (y), as well as the time_steps number. The process generates target values (ys) and input sequences (Xs) by swiping a time_step window across the data. The target value, ys, is the value that comes after the window in the input sequence Xs, which consists of time_steps consecutive feature values.
LSTM is particularly effective for long-term memory retention and avoids the vanishing gradient issue. It functions using a chain of memory blocks, where each block has gates that regulate the flow of information. There are three types of gates. The input gate controls what information is written into the memory cell; the forget gate determines what information should be kept or erased; the output gate controls the data read from the memory cell.
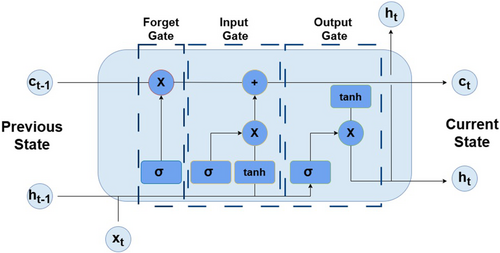
Finally, the output of the LSTM model is achieved [34].
Time series data contains both linear and nonlinear elements. ARIMA is effective at predicting average trends for linear patterns but struggles with capturing nonlinear aspects. On the other hand, LSTM excels at modeling nonlinear patterns. By sequentially combining LSTM with ARIMA, the ensemble model leverages the strengths of both, enabling it to identify and represent both linear and nonlinear patterns in the data.
2.3.2 Proposed model approach
The proposed model utilizes a bidirectional LSTM architecture to process sequential data of shape (n_input, n_features). The first Bidirectional-LSTM layer with 128 units and tanh activation captures long-term dependencies in both directions of the sequence, with return_sequences=True preserving the sequence length for further processing. A Dropout layer with a rate of 0.3 is then applied to prevent overfitting. The second Bidirectional-LSTM layer with 64 units extracts higher-level features, followed by Batch Normalization to normalize activations and accelerate training. A Dense layer with 64 units and tanh (hyperbolic tangent) activation introduces nonlinearity. Another Dropout layer (0.3) is included for regularization. Finally, a single output neuron with linear activation predicts the target value. The RMSprop optimizer with a learning rate of 0.001, is used to efficiently navigate the error surface during training. The model is optimized using the MSE loss function, which is ideal for continuously estimating real-valued outputs. To prevent overfitting, early stopping with a patience of five epochs is implemented, halting training if the validation loss does not improve over successive epochs, which saves the best model weights during the training process.
2.3.3 Pseudo Code
| Algorithm 1. Proposed model. |
| //df is the original data set from Johns Hopkins Github Repo |
| function createData(df) |
| setIndex ← Country/Region |
| country_df ← selectCountry(df) |
| transpose(Country_df) |
| data ← toDataFrame(country_df) |
| RenameColumn(“Total Confirmed,”“CountryName”) |
| return data |
| //data is available globally |
| data ← createData(df) |
| function visualizeData(data) |
| Plot(data) |
| function ARIMA(data) |
| P-value (PV) ← ADFtest(data) |
| if PV > 0.05 then |
| while PV > 0.05 |
| differenced_data ← diff(data) |
| increment(d) |
| p ← pacfPlot(differenced_data) |
| q ← acfPlot(differenced_data) |
| train,test ← Split(data,80%) |
| model← ARIMA(train,p,d,q) |
| pred ← fitArima(model,test) |
| res ← resid(fitArima(model,test)) |
| return pred,train_res,test_res |
| function LSTM(train_res,test_res) |
| train,test ← minMaxScaler(train_res,test_res) |
| strain,sval ← Split(train,80%) |
| model ← createModel(layers,hyperparamters) |
| fmod ← fitModel(model) |
| res_pred ← predict(fmod) |
| return res_pred |
| function Result() |
| pres, train_res, test_res ← ARIMA(data) |
| final_res ← pred + LSTM(train_res, test_res) |
| MAPE(final_res) |
| SMAPE(final_res) |
| MDAPE(final_res) |
2.4 Performance evaluation metrics
A time series model's correctness can be assessed by contrasting the expected and actual/true values. Although there are other performance indicators available, MAPE, SMAPE, and median absolute percentage error (MDAPE) are the ones used in this study. They are explained as follows:
2.4.1 MAPE
A lower MAPE indicates a more accurate model, with 0% being a perfect prediction (no error).
2.4.2 SMAPE
Like MAPE, a lower SMAPE indicates better predictive accuracy.
2.4.3 MDAPE
Median function calculates the middle value in a sorted list of absolute percentage errors.
In each case, the multiplication by 100 indicates that the final result is expressed as a percentage error.
3 RESULTS
India, Brazil, Russia, and the United States were chosen for examination because of their distinct pandemic paths and notable effects on worldwide COVID-19 data. This choice guarantees a thorough assessment of the model in various geographical areas and epidemic patterns, emphasizing its resilience and flexibility to changing data attributes.
Tables 2–5 represent the comparison of error metrics for India, Brazil, Russia, and the United States, respectively.
| Country | Category | Model | MAPE (%) | SMAPE (%) | MDAPE (%) |
|---|---|---|---|---|---|
| India | Baseline model | ARIMA | 3.75 | 3.65 | 3.54 |
| Prophet | 15.47 | 13.88 | 14.23 | ||
| LSTM | 3.81 | 3.73 | 3.86 | ||
| GRU | 2.81 | 2.77 | 2.80 | ||
| Hybrid model | ARIMA+ANN | 2.66 | 2.69 | 2.59 | |
| Proposed model | ARIMA+LSTM | 2.46 | 2.47 | 2.55 |
- Abbreviations: ANN, artificial neural network; ARIMA, auto-regressive integrated moving average; GRU, Gated Recurrent Unit; LSTM, long short-term memory; MAPE, mean absolute percentage error; MDAPE, median absolute percentage error; SMAPE, symmetric mean absolute percentage error.
| Country | Category | Model | MAPE (%) | SMAPE (%) | MDAPE (%) |
|---|---|---|---|---|---|
| Brazil | Baseline model | ARIMA | 1.28 | 1.30 | 0.76 |
| Prophet | 3.33 | 3.21 | 2.37 | ||
| LSTM | 7.72 | 7.43 | 7.42 | ||
| GRU | 0.96 | 0.96 | 1.00 | ||
| Hybrid model | ARIMA+ANN | 1.64 | 1.66 | 1.10 | |
| Proposed model | ARIMA+LSTM | 0.96 | 0.96 | 0.80 |
- Abbreviations: ANN, artificial neural network; ARIMA, auto-regressive integrated moving average; GRU, Gated Recurrent Unit; LSTM, long short-term memory; MAPE, mean absolute percentage error; MDAPE, median absolute percentage error; SMAPE, symmetric mean absolute percentage error.
| Country | Category | Model | MAPE (%) | SMAPE (%) | MDAPE (%) |
|---|---|---|---|---|---|
| Russia | Baseline model | ARIMA | 5.53 | 5.72 | 5.88 |
| Prophet | 13.77 | 12.56 | 12.38 | ||
| LSTM | 8.40 | 8.05 | 9.01 | ||
| GRU | 4.03 | 4.11 | 4.01 | ||
| Hybrid model | ARIMA+ANN | 3.10 | 3.13 | 3.17 | |
| Proposed model | ARIMA+LSTM | 2.89 | 2.92 | 2.98 |
- Abbreviations: ANN, artificial neural network; ARIMA, auto-regressive integrated moving average; GRU, Gated Recurrent Unit; LSTM, long short-term memory; MAPE, mean absolute percentage error; MDAPE, median absolute percentage error; SMAPE, symmetric mean absolute percentage error.
In Table 2, the best-performing benchmark model was GRU, which achieved a MAPE score of 2.81%, closely followed by the ARIMA+ANN with a MAPE score of 2.66%.
However, the hybrid model that combines ARIMA and LSTM outperformed both benchmark models with a MAPE score of 2.46%. It also demonstrated superior performance in terms of MDAPE and SMAPE, surpassing the ARIMA+ANN model even when using the same hyperparameters.
The decision to use MAPE as the primary evaluation metric stems from its scale independence and interpretability. Since MAPE is not influenced by the magnitude of the values in the data set, it is highly useful for comparing accuracy across time series data set. MAPE emphasizes proportional errors rather than absolute errors, making it ideal for evaluating model performance on data sets with varying scales.
Additionally, the other performance metrics used in this study are SMAPE and MDAPE. MDAPE uses the median instead of the mean to calculate the absolute percentage error. This makes MDAPE less sensitive to outliers, which improves the generalizability of the model. SMAPE avoids issues like division by zero error and undefined MAPE values, providing a more robust measure of model accuracy.
Tables 3–5 compare the performance metrics for Brazil, Russia and the United States. The proposed ARIMA-LSTM hybrid model outperformed both the hybrid ARIMA-ANN model and the baseline models, as demonstrated in the tables. Figure 4 showcases the MAPE values for various models applied to different country data sets such as India, Brazil, Russia, and the United States, respectively.
| Country | Category | Model | MAPE (%) | SMAPE (%) | MDAPE (%) |
|---|---|---|---|---|---|
| The United States | Baseline model | ARIMA | 3.57 | 3.47 | 3.63 |
| Prophet | 5.80 | 5.48 | 3.27 | ||
| LSTM | 7.96 | 7.66 | 7.96 | ||
| GRU | 3.24 | 3.30 | 3.24 | ||
| Hybrid model | ARIMA+ANN | 5.05 | 5.17 | 4.75 | |
| Proposed model | ARIMA+LSTM | 2.75 | 2.77 | 2.85 |
- Abbreviations: ANN, artificial neural network; ARIMA, auto-regressive integrated moving average; GRU, Gated Recurrent Unit; LSTM, long short-term memory; MAPE, mean absolute percentage error; MDAPE, median absolute percentage error; SMAPE, symmetric mean absolute percentage error.
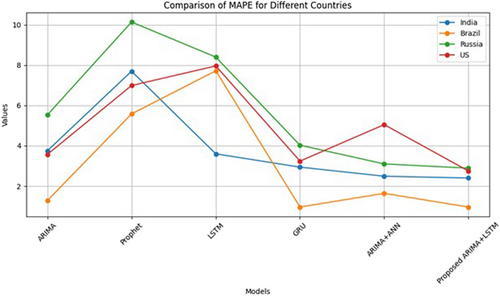
Figure 4 compares the MAPE values of various models, with different colors representing different countries. The models compared include ARIMA, Prophet, LSTM, GRU, ARIMA+ANN, and the proposed ARIMA+LSTM model. The results indicate that traditional models like ARIMA and Prophet exhibit relatively high MAPE values, particularly for India and Russia, reflecting lower predictive accuracy. In contrast, deep learning models such as LSTM and GRU demonstrate improved performance, with lower MAPE values, especially for Brazil and the United States. The ARIMA+ANN hybrid model further reduces the error across all countries, but the proposed ARIMA+LSTM model achieves the lowest MAPE values overall, indicating superior predictive accuracy. This is particularly evident in Brazil and the United States, where the proposed model significantly outperforms the others. These findings suggest that the combination of ARIMA with LSTM captures complex time-series patterns more effectively, making the hybrid ARIMA+LSTM model a robust choice for forecasting tasks in various contexts.
Figure 5 illustrates the comparison of actual outcomes versus predicted outcomes using the proposed ensemble ARIMA-LSTM approach for India (a), Brazil (b), Russia (c), and the United States (d), respectively.
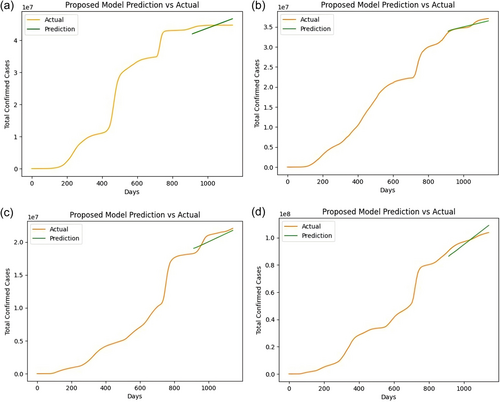
Figure 5 illustrates the performance of the proposed ARIMA+LSTM model in predicting the total confirmed COVID-19 cases over time for four countries: India, Brazil, Russia, and the United States. The green lines represent the model's predictions, while the yellow lines depict the actual observed data. Across all four countries, the model's predictions closely follow the actual data trends, indicating that the proposed model effectively captures the underlying patterns in the time-series data. In particular, the prediction accuracy is notable in Brazil and the United States, where the predicted and actual lines almost overlap, reflecting a high degree of precision. While there are minor deviations in India and Russia, the model still performs well, accurately reflecting the general trend of the pandemic in these countries. Overall, these plots validate the effectiveness of the proposed ARIMA+LSTM model in forecasting COVID-19 cases across diverse regions.
4 DISCUSSION
The proposed model has demonstrated superior performance, achieving the best MAPE score compared to all other models for each of the countries studied. Beyond MAPE, the model also outperformed other models using MDAPE and SMAPE metrics. The model performed particularly well in predicting confirmed COVID-19 cases in Brazil, where its predictions align closely with actual data. This enhanced forecast accuracy in Brazil may be due to the country's pandemic trajectory showing clearer patterns, making it easier for the hybrid ARIMA-LSTM model to capture trends, seasonality, and nonlinear relationships in the data. For the other countries, the proposed model also produced promising results, aligning closely with the actual time series data, as represented in the graphs. The proposed architecture could help the healthcare industry in early decision-making, leveraging its high precision to help improve future preparedness. This model can be especially useful in targeting interventions for demographics at higher risk, improving hospital system preparedness, and ultimately improving patient outcomes. One of the main challenges encountered during the implementation of the proposed model was overfitting. To address this, early stopping was used to improve generalizability. While the hybrid ARIMA-LSTM ensemble technique is more accurate, it does involve a trade-off between time and accuracy. The hybrid model takes approximately 296 s to run, whereas the combined baseline models take only 47 s. However, in the context of a healthcare crisis or pandemic, the hybrid model's superior accuracy justifies the additional time, making it a valuable tool for more secure healthcare systems and response strategies.
The Ensemble ARIMA-LSTM model can be used in future research to forecast outbreaks and guide resource distribution in the chosen nations (the United States, Brazil, Russia, and India). Using our model, the following approaches to resource allocation and outbreak preparedness are proposed: Pre-emptive Resource Allocation—Based on the model's estimates, identify high-risk areas and preallocate healthcare resources, such as hospital beds, ventilators, and medical supplies, Targeted Preventive Measures—Use the model's predictions to improve the efficacy of measurably high-risk areas by implementing limited lockdowns, mass testing, and vaccination programs, Dynamic Healthcare Personnel Deployment—Make sure that medical professionals and personnel are easily accessible when they are most needed by optimizing the deployment of healthcare professionals and support staff to high-risk regions that the model has identified. By comparing scenarios with and without the model's predictions, these tactics can be quantified, showcasing the model's enormous potential and benefit in improving public health readiness and responses.
5 CONCLUSIONS
The article proposes a hybrid ARIMA-LSTM model that predicts COVID-19 cases more accurately than traditional base models. The model offers significant potential to improve healthcare preparedness by allowing for earlier decision-making, targeted interventions, and better hospital resource allocation. Although the model is more complex and requires longer runtimes than simpler models, its improved accuracy makes it a valuable tool for managing pandemics. The paper also suggests that this model could be adapted for future outbreaks, with the potential to incorporate additional environmental factors for even better predictions. While the model was tested using data from Brazil, Russia, India, and the United States, it may perform differently in other nations with distinct epidemic patterns and healthcare systems. Therefore, further validation in different nations and under varying circumstances would be necessary to ensure its generalizability. Despite outperforming the benchmark models in this study, newer developing models and methodologies not taken into consideration here may challenge the model's performance. To maintain its relevance and accuracy, the ARIMA-LSTM model should be regularly updated and compared to newer models. Looking ahead, the development of hybrid model-based real-time forecasting systems could provide public health authorities with up-to-date forecasts, enabling prompt decision-making and action. Furthermore, enhancing the model's input by employing multivariate time series analysis could further improve its predictive power. Including extra data sources such as mobility data, vaccination rates, social media trends, and healthcare capacity could significantly boost the model's performance and make it even more robust for future public health challenges.
AUTHOR CONTRIBUTIONS
Somit Jain: Conceptualization; data curation; formal analysis; investigation; methodology; resources; software; validation; visualization; writing—original draft preparation; writing—review and editing (equal). Shobhit Agrawal: Conceptualization; data curation; formal analysis; investigation; methodology; resources; software; validation; visualization; writing—original draft preparation; writing—review and editing (equal). Eshaan Mohapatra: Conceptualization; data curation; formal analysis; investigation; methodology; resources; software; validation; visualization; writing—original draft preparation; writing—review and editing (equal). Kathiravan Srinivasan: Methodology; project administration; resources; supervision; validation; visualization; writing—original draft preparation; writing—review and editing.
ACKNOWLEDGMENTS
None.
CONFLICT OF INTEREST STATEMENT
The authors declare no conflict of interest.
ETHICS STATEMENT
Not applicable.
INFORMED CONSENT
Not applicable.
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are openly available in CSSEGISandData/COVID-19 at https://github.com/CSSEGISandData/COVID-19/blob/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv, reference number [32].




