Correlation for the Sauter Mean Diameter of a Prefilmer Airblast Atomizer at Varying Operating Conditions
Abstract
One of the key factors that affect the combustion performance in gas turbines and therefore the amount of pollutant emission and the efficiency is the atomization quality of the liquid fuel. Often reliable droplet size distributions for combustion simulations are missing. In this work a correlation for the Sauter mean diameter based on energy equilibrium is derived and compared to results from three-dimensional numerical simulation of the atomization of a liquid film and to an empirical correlation from the literature. It is shown that the derived correlation agrees better with the results of the simulations than the empirical correlation.
1 Introduction
The more stringent requirements in the design of combustion systems for aero engine applications to enhance efficiency and to lower pollutant emissions require, amongst others, the optimization of the injection system 1 as the atomization process is one of the main factors influencing the combustion performance 2. One technical implementation for injection systems is the airblast atomizer. It creates a thin kerosene film on the inner wall of a cylinder called prefilmer. A parallel fast flowing air stream accelerates the liquid fuel which is supposed to disintegrate at the end of the prefilmer (atomizing lip).
Due to the limited computational resources it is difficult to simulate the whole atomization process in combination with the combustion in a single calculation in a reasonable time. Therefore, the primary formation process of the spray is often neglected in combustion simulations. Instead, droplet size distributions, which are measured downstream of the atomizer, are used as initial conditions 3 or even empirical correlations 6. The disadvantage is that those measurements normally run at lower pressure than the technical application due to the limited applicability of the measurement techniques to high pressure. However, the phenomenon called surface stripping (separation of droplets of the interface from a liquid film 11), which gets important at high working pressure, changes the droplet size distribution. Therefore, the use of a droplet size distribution measured at low pressure in a simulation at higher pressure is not possible without uncertainties.
In 12 an energy equilibrium is used to derive a correlation for the generated Sauter mean diameter of the atomization of a liquid sheet produced by a flat-sheet airblast atomizer. The same procedure is used for the derivation of a correlation for the Sauter mean diameter of an atomized liquid jet generated by a plain-jet airblast atomizer. Based on the idea of the energy equilibrium a correlation for the Sauter mean diameter of an atomized liquid jet produced by an external-mixing twin-fluid atomizer is derived in 13. In comparison to the work of Lefebvre 12, this correlation is not only fitted to experimental results at different pressure with the help of fit parameters, but also with the help of exponents.
In the presented work the energy equilibrium is adapted to a simplified planar prefilmer airblast atomizer. The proportionality factors of this correlation are determined with the help of numerical simulations of a three-dimensional multiphase flow. The results of the derived correlation are compared to a correlation from literature 10 that is based on experimental results at atmospheric conditions. In those experiments, amongst others, the air velocity, surface tension and liquid viscosity is changed to investigate the influence on the produced droplet size.
In this work it is shown that the newly derived correlation agrees well with the results from the numerical simulations, so that more reliable boundary conditions for combustion simulations can be gained with the help of the presented correlation.
2 Numerical Models
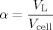 (1)
(1) (2)
(2)where the index L denotes the liquid and the index G the gas phase.
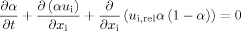 (3)
(3)where t describes the time, ui the velocity in xi-direction and ui,rel the relative interface velocity 16. The third term on the left hand side describes the artificial compression of the interface of the fluids to reduce the numerical diffusion.
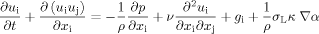 (4)
(4)where κ denotes the curvature of the interface.
The turbulence is modeled with the k-ϵ turbulence model, which is adapted for two-phase flows. The volume of fluid method and the adapted k-ϵ turbulence model for two-phase flows are described in detail in 18.
3 Numerical Setup
The numerical setup is the same as in 18 and is shown in Fig. 1. The wedge separates the liquid and gas phase entry before the fluids interact on the prefilmer. The cubical cells of the computational grid have an edge size of 30 µm and are equidistantly distributed into the flow direction (y-axis).
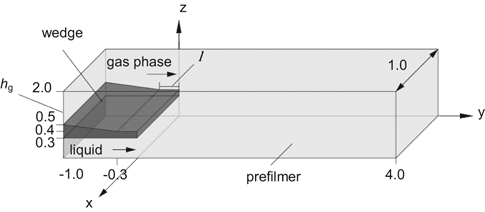
Computational domain (all dimensions in [mm]).
The operating conditions of the investigated case are listed in Tab. 1. The gas properties are taken from REFPROP 8 19. The standard gas phase is air and the standard liquid is kerosene. The calculation of the kerosene properties are based on 20 for an ambient temperature of 20 °C (density ρL = 805.48 kg m−3). A fully developed liquid velocity profile is used as boundary condition with a mean velocity of vL = 1 m s−1. The air inlet velocity is varied in a range of 30 to 90 m s−1. Additionally, the influence of the pressure is investigated between 2 and 12 bar. For the investigation of the influence of surface tension σL and gaseous kinematic viscosity νG these parameters are varied separately. Consequently, the properties of the liquid and gas phase chosen for some of the simulations do not correspond to realistic fluids.
| Case | vG [m s−1] | p [bar] | ρG [kg m−3] | νG [mm2 s−1] | νL [mm2s−1] | σL [10−3 N m−1] | We [–] |
|---|---|---|---|---|---|---|---|
| 1 | 60 | 6 | 7.14 | 2.57 | 1.82 | 22.8 | 338 |
| 2 | 30 | 6 | 7.14 | 2.57 | 1.82 | 22.8 | 84 |
| 3 | 40 | 6 | 7.14 | 2.57 | 1.82 | 22.8 | 150 |
| 4 | 90 | 6 | 7.14 | 2.57 | 1.82 | 22.8 | 760 |
| 5 | 60 | 2 | 2.38 | 7.68 | 1.82 | 22.8 | 112 |
| 6 | 60 | 3 | 3.57 | 5.12 | 1.82 | 22.8 | 169 |
| 7 | 60 | 4 | 4.76 | 3.84 | 1.82 | 22.8 | 225 |
| 8 | 60 | 6 | 7.14 | 2.57 | 1.82 | 9.8 | 790 |
| 9 | 60 | 6 | 7.14 | 2.57 | 1.82 | 49.2 | 157 |
| 10 | 90 | 6 | 7.14 | 2.57 | 1.82 | 9.8 | 1776 |
| 11 | 90 | 6 | 7.14 | 2.57 | 1.82 | 49.2 | 353 |
| 12 | 60 | 6 | 7.14 | 1.285 | 1.82 | 22.8 | 338 |
| 13 | 60 | 6 | 7.14 | 5.14 | 1.82 | 22.8 | 338 |
| 14 | 60 | 3 | 3.57 | 5.12 | 1.82 | 11.4 | 338 |
| 15 | 42.4 | 6 | 7.14 | 2.57 | 1.82 | 11.4 | 338 |
| 16 | 42.4 | 12 | 14.29 | 1.29 | 1.82 | 22.8 | 338 |
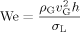 (5)
(5)4 Analysis Methods
The complex surface topology existing of breaking waves, ligaments and droplets on the film initiated by the fast moving gas flow is shown in Fig. 2. The arrows mark the definition of the film thickness. As a consequence of this definition, droplets above the film and the upper part of breaking waves are not considered.

Determination of the film thickness (liquid is marked with gray color).
550 time steps with a time difference of 10−4 s have been analyzed for each case of Tab. 1. The droplets and ligaments consist of those cells that are filled with liquid (α ≥ 0.5) and are not considered in the determination of the film thickness as illustrated in Fig. 3. In the shown two-dimensional plane the white cells mark the gaseous phase (α < 0.5) and the gray cells the liquid phase (α ≥ 0.5). The gray cells with a black number 1 represent the liquid film, while droplets are represented by gray cells with a white number 1. In the two-dimensional case a droplet is a region of cells that are connected with the edges of the neighbor cells and filled with liquid (α ≥ 0.5). Therefore, three droplets are shown in Fig. 3. If two neighbor cells are only connected with one corner of those cells, it is assumed that they belong to two different droplets.

Determination of droplet volumes.
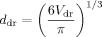 (6)
(6)This calculation step is performed for every droplet at every considered time step on the prefilmer in order to describe the whole emerging droplet collective.
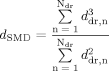 (7)
(7)The number of all considered droplets is Ndr.
5 Derivation of a Correlation Based on Energy Balance
Based on the above mentioned simulations a correlation for the Sauter mean diameter dSMD is derived in a similar way as described in 12, 19. The main idea of the derivation is that energy is necessary to increase the surface of a liquid phase when waves and droplets are formed against the surface tension of the liquid. The energy necessary for this process is transferred from the gas phase to the liquid phase. Equating both energies results in the correlation of the Sauter mean diameter.
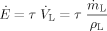 (8)
(8)with 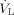 being the volume flow of the liquid film, which is the ratio of the mass flow of liquid
being the volume flow of the liquid film, which is the ratio of the mass flow of liquid 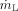 to the density of the liquid ρL. The acceleration of the film due to the shear stress depends on the volume flow of the liquid. The probability for the formation of ligaments and droplets increases with higher acceleration of the film.
to the density of the liquid ρL. The acceleration of the film due to the shear stress depends on the volume flow of the liquid. The probability for the formation of ligaments and droplets increases with higher acceleration of the film.
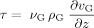 (9)
(9) (10)
(10)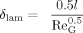 (11)
(11) (12)
(12)with the characteristic length hG being the height of the domain in which the gas phase enters it (hG = 1.5 mm).
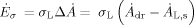 (14)
(14)where Δ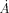 is the increase of the surface per second due to the formation of droplets.
is the increase of the surface per second due to the formation of droplets.
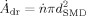 (15)
(15) being the number of produced droplets per second. The mass flow of droplets is:
being the number of produced droplets per second. The mass flow of droplets is:
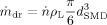 (16)
(16)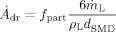 (18)
(18) (19)
(19) (20)
(20)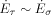 (21)
(21) (22)
(22) (23)
(23)The two unknown constants are determined using results of the numerical simulations together with error minimization by the least squares method to flam = 2.23 and fpart = 0.34. This result can be interpreted that 34 % of the liquid is atomized on its way on the prefilmer. The root mean square of the least squares method is 0.0002.
6 Results and Discussion
 (24)
(24)where the characteristic length lc is the initial height of the liquid film (lc= 300 µm) and l is the length of the prefilmer (l = 4 mm). The factors f1 = 44.78 and f2 = 1.02 have been determined with the least squares method to minimize the difference between the results of Eq. 24 and the simulations. The method results in a root mean square error of 0.0004.
This correlation is used for example in 21 and 23 for the comparison with experimental data. It is shown that the correlation can predict the experimental results, but more often it fails.
For comparison the Sauter mean diameter of the numerical simulations (filled symbols) are plotted together with the Sauter mean diameter calculated with the correlation (23) (empty symbols and marked with “corr”) in Fig. 4. The numbers in the legends correspond to the case number of the parameter variation given in Tab. 1. For a better overview, the cases are ordered in such a way that the varied parameter increases from top to bottom in the legend. In addition, the results from the empirical correlation Eq. 24 are included in Fig. 4 and marked with “lit”.

Comparison of the numerical results with the correlations. a) Variation of gas velocity; b) variation of working pressure; c) variation of surface tension; d) variation of gaseous kinematic viscosity; e) constant Weber number We = 338.
Fig. 4a shows that the Sauter mean diameter from both, the simulations and from the derived correlation Eq. 23, agree qualitatively and quantitatively well with each other. The correlation from literature (Eq. 24) instead captures only the tendencies. For high gas velocity the deviations from the results of the correlation Eq. 23 is over ten times smaller than the deviation of correlation Eq. 24 from the simulations.
As illustrated in Fig. 4b the dependency of the working pressures is correctly described from the results of the correlation derived in this work (see Eq. 23). The following comparison emphasizes the important influence of the gas velocity on the atomization process as it is reported in literature 8, 10: by an increase of the working pressure of a factor of 2 (from 3 to 6 bar), the Sauter mean diameter of the correlation decreases by approximately 13 % and the Sauter mean diameter of the simulation by approximately 28 %. Increase of the gas velocity by a factor of 2 (from 30 to 60 m s−1) results in a decrease of the Sauter mean diameter of the correlation by approximately 32 % and for the simulation by approximately 40 %. The correlation from the literature Eq. 24 captures this tendency, but the difference between its results and the data from the simulation increases for lower (2 bar) and higher pressure (6 bar).
Fig. 4c shows the comparison of the results of the Sauter mean diameter by a variation of the surface tension for the gas velocity of 60 and 90 m s−1. The same tendency is observed for the simulation and the derived correlation Eq. 23: the Sauter mean diameter increases with higher surface tension. Furthermore, the Sauter mean diameter decreases for a constant surface tension but increasing velocity of the gas phase. The correlation from the literature Eq. 24 again is able to capture the tendencies, but underestimates the results.
The influence of the kinematic viscosity of the gaseous phase on the Sauter mean diameter is shown in Fig. 4d. The diameter slightly decreases with higher kinematic viscosity. The derived correlation from the literature Eq. 24 predicts a constant Sauter mean diameter because Eq. 24 does not depend on the kinematic viscosity.
Fig. 4e shows the Sauter mean diameter in dependency of the working pressure for a constant Weber number We = 338. As a result of the comparison it can be stated that the Weber number is not sufficient to consider all the relevant effects of the simulated atomization process (as it is also reported in 21). This conclusion is based on the fact that different diameters are observed by the variation of the parameters of the constant Weber number. The maximum deviation of the Sauter mean diameter from the simulation is 18 % and from Eq. 23 23 %. The variation of the results can also be used to show the influence of different parameters. At a constant surface tension (case 16 and 17, 1 and 18) the Sauter mean diameter increases by a decrease of gas velocity and an increase of working pressure. Consequently smaller droplets are created by higher gas velocity. The correlation from the literature Eq. 24 instead predicts that the Sauter mean diameter decreases with increasing pressure.
Summarizing the above shown results the Sauter mean diameter of the correlations are plotted against the Sauter mean diameter from the numerical simulations (Fig. 5). The overview depicts the improved capability of the newly derived correlation to resemble the Sauter mean diameter from the detailed simulations. The averaged difference between the Sauter mean diameter of the simulation and the derived correlation Eq. 23 is 41 µm whereas the averaged difference between the Sauter mean diameter of the simulation and of the correlation from the literature Eq. 24 is 79 µm. The constant deviation of the Sauter mean diameter of the simulation is ± 25 % (dotted line), while the deviation of the correlation from the literature is ± 50 % (dashed line).
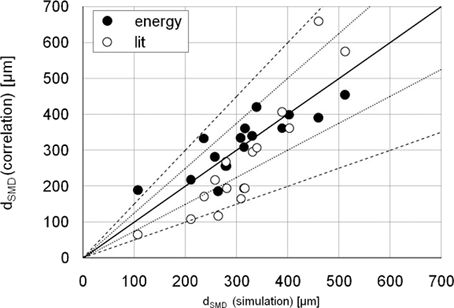
Comparison of the Sauter mean diameter of the correlations.
7 Conclusion
A broad range of parameters influencing the Sauter mean diameter of droplets which are separated from a liquid film on a prefilmer of a simplified airblast atomizer are simulated. The results show that the Sauter mean diameter depends mainly on the gas velocity. These results are compared with a correlation that has been derived considering the equilibrium of the energy which is necessary to increase a liquid surface and the energy which is transferred by the shear stress from the gas to the liquid phase, and a correlation from literature. Qualitatively and quantitatively there is a good agreement between the Sauter mean diameter from the correlation derived in the current work and from numerical simulations. The literature correlation instead is able to capture most tendencies, but fails when reproducing the absolute values.
Acknowledgements
The authors gratefully acknowledge the financial support by the federal state Baden-Württemberg, Germany through the project “Future Offensive IV: Innovation and Excellence“. The computation time has been kindly provided by the Steinbuch Centre for Computing of the Karlsruhe Institute of Technology.
Symbols used
-
 [m2s−1]
[m2s−1] -
surface flow
-
- d [m]
-
diameter
-
- dSMD [m]
-
Sauter mean diameter
-
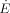 [J s−1]
[J s−1] -
energy flow
-
- f [–]
-
factor
-
- gi [m s−2]
-
gravitational component in i-direction
-
- h [m]
-
height
-
- l [m]
-
length
-
 [kg s−1]
[kg s−1] -
mass flow
-
 [s−1]
[s−1] -
number per second
-
- p [N m−2]
-
working pressure
-
- Re [–]
-
Reynolds number
-
- u, v, w [m s−1]
-
velocity components in x, y, z-direction
-
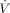 [m3s−1]
[m3s−1] -
volume flow
-
- We [–]
-
Weber number
-
- x, y, z [m]
-
Cartesian coordinates
Greek symbols
-
- α [–]
-
liquid volume fraction
-
- κ [m−1]
-
curvature
-
- δlam [m]
-
laminar boundary thickness
-
- ν [m2s−1]
-
kinematic viscosity
-
- ρ [kg m−3]
-
density
-
- σ [N m−1]
-
surface tension
-
- τ [N m−2]
-
shear stress
Subscripts
-
- c
-
characteristic
-
- cell
-
mesh cell
-
- G
-
gas phase
-
- i
-
running index (i = 1, 2, 3)
-
- j
-
running index (j = 1, 2, 3)
-
- dr
-
droplet
-
- L
-
liquid
-
- lam
-
laminar
-
- part
-
partial
-
- s
-
surface







