Volume 4, Issue 3 e317

REVIEW ARTICLE

Open Access

Deep learning for predicting synergistic drug combinations: State-of-the-arts and future directions

Yu Wang,

Yu Wang

Putuo District Ganquan Street Community Healthcare Center, Shanghai, China

Search for more papers by this author

Junjie Wang,

Junjie Wang

orcid.org/0000-0003-0732-051X

Department of Medical Informatics, School of Biomedical Engineering and Informatics, Nanjing Medical University, Nanjing, China

Search for more papers by this author

Yun Liu,

Corresponding Author

Yun Liu

[email protected]

Department of Medical Informatics, School of Biomedical Engineering and Informatics, Nanjing Medical University, Nanjing, China

Department of Information, the First Affiliated Hospital, Nanjing Medical University, Nanjing, China

Correspondence

Yun Liu, Department of Information, the First Affiliated Hospital, Nanjing Medical University, Nanjing, 210029, China.

Email: [email protected]

Search for more papers by this author

Yu Wang,

Yu Wang

Putuo District Ganquan Street Community Healthcare Center, Shanghai, China

Search for more papers by this author

Junjie Wang,

Junjie Wang

orcid.org/0000-0003-0732-051X

Department of Medical Informatics, School of Biomedical Engineering and Informatics, Nanjing Medical University, Nanjing, China

Search for more papers by this author

Yun Liu,

Corresponding Author

Yun Liu

[email protected]

Department of Medical Informatics, School of Biomedical Engineering and Informatics, Nanjing Medical University, Nanjing, China

Department of Information, the First Affiliated Hospital, Nanjing Medical University, Nanjing, China

Correspondence

Yun Liu, Department of Information, the First Affiliated Hospital, Nanjing Medical University, Nanjing, 210029, China.

Email: [email protected]

Search for more papers by this author

First published: 17 June 2024

https://doi.org/10.1002/ctd2.317

Share a link

Email
Wechat
Bluesky

Abstract

Combination therapy has emerged as an efficacy strategy for treating complex diseases. Its potential to overcome drug resistance and minimize toxicity makes it highly desirable. However, the vast number of potential drug pairs presents a significant challenge, rendering exhaustive clinical testing impractical. In recent years, deep learning-based methods have emerged as promising tools for predicting synergistic drug combinations. This review aims to provide a comprehensive overview of applying diverse deep-learning architectures for drug combination prediction. This review commences by elucidating the quantitative measures employed to assess drug combination synergy. Subsequently, we delve into the various deep-learning methods currently employed for drug combination prediction. Finally, the review concludes by outlining the key challenges facing deep learning approaches and proposes potential challenges for future research.

1 INTRODUCTION

The practice of combining multiple pharmaceutical agents for disease treatment, known as drug combination therapy, is commonly employed for complicated diseases including cancer,^1-3 hypertension^{4, 5} and infectious diseases.^6-8 Compared to monotherapy, drug combination therapy offers several advantages such as improved efficacy and reduced side effects and toxicity. However, it is important to note that not all drug combinations exhibit synergistic effects; in fact, some combinations may show antagonistic effects.⁹ For example, remdesivir with amodiaquine to treat coronavirus disease 2019 shows a strong antagonistic effect.¹⁰

Early studies on screening drug combination synergy typically rely on wet-lab experiments, which are characterized by their time-consuming nature and considerable cost implications.¹¹ Furthermore, drug combination trials carry inherent risks of adverse side effects or potentially harmful reactions. Consequently, preclinical strategies have emerged as vital tools for identifying and assessing drug combinations within the context of cancer research.

With the accumulation of large-scale datasets, computational approaches have emerged as an alternative for efficiently screening and prioritizing candidate drug pairs. For example, Li et al.¹² proposed a random forests-based method for predicting synergistic anticancer combinations. Meng et all.¹³ trained an extreme gradient boosting (XGBoost) to predict the synergistic drug combinations using the features by runing struc2vec on protein interaction network. Sidorov et al.¹⁴ also proposed an XGBoost-based model, but it trains a unique model for each cell line.

Deep learning-based methods have garnered significant attention across various research domains in bioinformatics, encompassing areas such as drug-target interaction,^{15, 16} hydrogel design and optimization,¹⁷ Organoids¹⁸ and drug design.¹⁹ These methods employ diverse architectures, including fully connected neural networks (FCNN), convolutional neural networks (CNNs),²⁰ Transformer networks²¹ and Graph Neural Networks (GNNs),²² which have demonstrated their efficacy in extracting meaningful features from raw data and effective modelling complex and high-dimensional datasets. Consequently, the prediction of drug combination synergy through deep learning approaches has emerged as a promising and advancing trend in this field.

This review comprehensively examines recent applications in the realm of deep learning-based drug combination synergy prediction. We start with an abridged overview of the synergy metrics employed in the drug combination synergy prediction task, alongside the datasets utilized for model development. Subsequently, the review delves into the latest developments in deep learning-based drug combination synergy prediction models. Finally, we outline the limitations and future research.

2 METRICS OF SYNERGISTIC EFFECT IN DRUG COMBINATIONS PREDICTION TASK

In deep learning-based drug combination synergy prediction models, synergy scores serve as the gold standard (label). However, a central challenge lies in the lack of consensus on a universal synergy criterion for characterizing the degree of synergistic effects. While several metrics exist, they each present distinct underlying assumptions and may not comprehensively capture the complexity of drug combinations. Among the most widely used metrics are the Loewe additivity model,²³ Bliss independence model,²⁴ highest single agents (HSAs),²⁵ and zero interaction potency (ZIP).²⁶

The Loewe additivity model assumes no self-interaction between drugs and interchangeability within a combination. According to this model, for two drugs a and b, the expected effect under Loewe additivity satisfies the equation:

\begin{equation} \def\eqcellsep{&}\begin{array}{*{20}{c}} {\frac{a}{A} + \ \frac{b}{B} = \ 1\ } \end{array} \end{equation}

()

where A and B represent the equivalent doses of drug A and drug B alone that produce the expected effect.

The Bliss operates under the assumption that the relative effect of each drug is independent of the other. The expected effect

{{E}_{AB}}

is thus articulated as:

\begin{equation} \def\eqcellsep{&}\begin{array}{*{20}{c}} {\ {{E}_{AB}} = {{E}_A}\ + {{E}_B} - {{E}_{AB}}} \end{array} \end{equation}

()

where

{{E}_A}

and

{{E}_B}

denote the monotherapy effect of drugs A and B, respectively.

The drug combination synergy effect is determined by the maximum effect of each drug under the HSA metric. Thus the expected effect

{{E}_{AB}}

can be given by:

\begin{equation} \def\eqcellsep{&}\begin{array}{*{20}{c}} {\ {{E}_{AB}} = {\mathrm{max}}({{E}_A}\ ,{{E}_B})} \end{array} \end{equation}

()

The expected effect under the ZIP metric is based on the concept that two drugs do not potentiate each other. Except for these metrics, there also exist other metrics including Combination Index (CI),²⁷ S score²⁸ and ComboScore.²⁹ Even though these metrics can provide a view to quantify synergy, no consensus exists. Besides, most of them do not distinguish the potency and efficacy. Recently, multi-dimensional Synergy of Combinations (MuSyC) aims to provide a more consistent and unbiased metric and model with the synergy by enhancing potency and/or efficacy of the single agents.^{30, 31} Following the MuSyC idea, SynBa uses the Baysian approach to estimate the synergistic.

As deep learning-based models are increasingly applied in real-world settings, the development of a standardized synergy metric becomes even more critical. While efforts towards unifying existing frameworks are ongoing, achieving consensus remains an unresolved issue. In the meantime, it is imperative that deep learning models be evaluated across multiple metrics to demonstrate their efficacy and reliability for future applications.

3 DEEP LEARNING BASED DRUG COMBINATION PREDICTION

The schematic representation of drug combination synergy prediction is illustrated in Figure 1. The foundational pipeline comprises four distinct stages: dataset preparation, input data processing, deployment of deep learning models, and model evaluation. In the dataset preparation stage, several crucial tasks are undertaken, including the selection of appropriate synergy score metrics and the filtering of the dataset to ensure its relevance and quality. Subsequently, careful consideration is given to the input data for the deep learning models, with an emphasis on capturing the intricate interactions between drugs and their effects. The design of the deep learning models constitutes a critical aspect of the process, requiring meticulous attention to detail to effectively capture the underlying complexities of drug combinations. Finally, the evaluation stage involves assessing the performance of the model using multiple metrics and methodologies to ensure robustness and reliability. we present a detailed investigation in terms of input data, datasets, models and evaluation in Figure 4.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Schematic view of the generic pipeline of deep learning-based models.

3.1 Datasets

The mechanisms underpinning deep learning-based drug combination prediction models are inherently data-driven, with their performance contingent upon the availability of large-scale datasets. In Table 1, we enumerate several datasets for reference. Except for these six datasets, there also exist some databases such as FORCINA, CLOUD, etc. It should be noted that these datasets show a significant overlap. These datasets play a crucial role in supplying the necessary volume and diversity of data essential for training and validating the predictive algorithms embedded within deep learning models. The accessibility of these drug synergy combination datasets enables the development and refinement of deep learning-based models, thereby advancing research in the field.

TABLE 1. Summary of drug synergy combination datasets.

Dataset	# of drugs	# of cell lines	# of drug pairs	# of combination	References
DrugComb	8397	2040	74421	751498	³²
O'Neil	38	39	583	22737	³³
DrugCombDB	2887	124	448555	6055926	³⁴
ALMANAC	104	60	5232	304549	²⁹
SYNERGxDB	1977	151	22507	536596	³⁵

It is important to note that the aforementioned drug synergy combination datasets primarily stem from in-vitro experiments and emphasize synthetic compound drugs. However, recent efforts have introduced in-silico models, such as CDCDB, curated from sources like ClinicalTrials.gov.³⁶ Additionally, the NPCDR dataset offers comprehensive molecular regulation data pertaining to natural product-based drug combinations across various disease cell lines and model organisms³⁷. These diverse datasets contribute to a more comprehensive understanding of drug synergy.

3.2 Input data

For deep learning-based models to accurately predict the synergy effects, it is imperative to incorporate relevant drug and cell features into the models. A thorough examination of the features utilized in recent models reveals that they can be categorized into two distinct classes: biological attributes and biological knowledge.

Biological attributes pertain to the inherent characteristics of drugs and cells that directly impact their interactions and subsequent effects. For drugs, common biological attributes include SMILES representations, drug structures, descriptors, and fingerprints. Conversely, for cell lines, key biological attributes encompass gene expression profiles, genomic mutations (MUT), copy number variations (CNV), and other genomic data.

In the domain of deep learning-based models, a variety of methods have been developed that leverage biological attributes to enhance predictive accuracy. DeepSynergy,³⁸ for example, utilizes molecular fingerprints and descriptors to characterize drugs, while gene expression data is employed to profile cell lines. This methodology has consistently demonstrated competitive performance across diverse scenarios. The approach adopted by DeepSynergy has been mirrored in other models such as MatchMaker³⁹ and SDCNet,⁴⁰ which also rely on similar input data for predictive purposes. Subsequent to DeepSynergy's establishment of this approach, there has been a shift in focus towards innovative representation of drug information. Some recent studies have eschewed the traditional reliance on fingerprints and descriptors, instead opting to model drug structures as graphs. These studies harness Graph Neural Networks (GNNs) to distil structural information from these graph representations. DeepDDS⁴¹ and AttenSyn⁴² exemplify this novel methodology, showcasing the potential of GNNs in capturing the intricate relationships within molecular structures to refine drug synergy predictions. Beyond drug feature exploration, research has also expanded to incorporate multi-omic data for cell line characterization. SynergyX, for instance, integrates six types of omic data, demonstrating enhanced predictive performance.⁴³ The findings from this study suggest that utilizing two or three types of omic data can yield robust results.⁴³ In light of the diverse drug features and varied cell line representations, CCSynergy introduces various levels of bioactivity profiles, providing a foundation for future research endeavours.⁴⁴

On the other hand, biological knowledge encompasses the vast array of information that has been accumulated through scientific research and experimentation. This includes but is not limited to, known drug-target interactions, and protein-protein interaction networks. Early works like TranSynergy⁴⁵ and GraphSynergy⁴⁶ use the PPI network to model the drug and cell line representations. KGANSynergy⁴⁷ uses multiple drug-related knowledge graphs to construct protein-related knowledge graphs for representing the drug and cell line. Except for the exploration of the external resources, some works also model the drug combination into a heterogeneous graph, such as Hypergraphsynergy,⁴⁸ CGMS⁴⁹ and HypertranSynergy⁵⁰.

3.3 Basic neural networks

Based on the related drugs and cell line information, modelling the intricate relationships via the neural networks to effectively predict the synergistic effects is a pivotal pursuit and challenging task. This survey aims to review the prevalent deep learning-based methodologies and categorize their underlying neural network architectures into distinct classes: FCNNs, RNNs, CNNs, GNNs, Attention and Transformer. Figure 2 presents the representative structures of these fundamental neural network types.

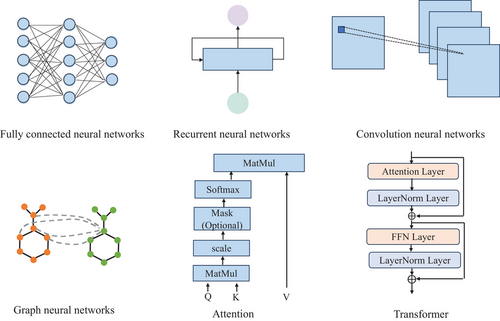
FCNNs are typically characterized by a set of learned weights and biases applied across all input features, which can be succinctly represented by the matrix multiplication formula $y\ = \ Wx + b$ , where $W,b$ denote the trainable weight matrix and bias vector, x represents the input features.

CNNs aim to capture the local patterns via convolutional operations. The convolutional operation applies several filters or kernels to input data to extract and represent spatial information in data. The convolution can be formulated as:

\begin{equation} \def\eqcellsep{&}\begin{array}{*{20}{c}} {\left( {f*g} \right)\ \left( t \right) = \mathop \smallint \limits_{\tau \in {{\Omega}}} g\left( \tau \right)f\left( {t + \tau } \right)d\tau \ } \end{array} \end{equation}

()

where

f( \cdot )

and

g( \cdot )

represent the feature and parametric kernel function.

{\mathrm{\Omega \ }}

represents a neighbourhood in a given space.

RNNs possess a distinct characteristic compared to FCNNs and CNNs which incorporate feedback loops. This allows the network to utilize its output at a prior time step

t - 1

as additional input for subsequent time steps

t

. As a consequence, RNNs demonstrate remarkable proficiency in handling sequential data. Given the input

{{x}_t}

at current time

t

and the corresponding hidden state

{{h}_{t - 1}}

which from the previous time

t - 1

output. The mathematical formulation for the update of the hidden state in an RNN is given by:

\begin{equation} \def\eqcellsep{&}\begin{array}{*{20}{c}} {\ {{h}_t} = \ tanh\left( {W\left[ {{{x}_t},{{h}_{t - 1}}} \right] + b} \right)} \end{array} \end{equation}

()

where

W\

and

\ b

are the trainable weights and bias, which are shared temporally.

The concept of Attention has initially been utilized in natural language processing tasks, allowing for explicit modelling of long-range dependencies in sequences and handling information derived from diverse representation spaces. An attention function maps queries (

Q

), keys (

K

), and values (

V

) to an output as follows:

\begin{equation} \def\eqcellsep{&}\begin{array}{*{20}{c}} {\ Attention\ \left( {Q,K,V} \right) = \ softmax\left( {\frac{{Q{{K}^T}}}{{\sqrt d }}} \right)V} \end{array} \end{equation}

()

where

\sqrt d

is the dimensionality of the query vector.

Building on the foundation of attention mechanisms, Vaswani et al.²¹ introduced the Transformer architecture, which exhibits exceptional capability in capturing long-range dependencies and contextual relationships within sequential data. The Transformer leverages an encoder-decoder structure. Given an input sequences, the encoder generates a contextualized representation, while the decoder utilizes this representation to generate the output sequences. Both the encoder and decoder comprise multiple identical layers. The core component of the Transformer is the multi-head attention mechanism (MHA). The MHA breaks down the input into multiple attention ‘heads’, each of which focuses on different subspace. These heads operate in parallel, focusing on extracting distinct features from the input. Following individual attention computations within each head, the resulting outputs are concatenated to form a comprehensive representation. Given the number of head as

h

, the MHA can be formulated as:

\begin{equation} \def\eqcellsep{&}\begin{array}{*{20}{c}} {MHA\ \left( {Q,K,V} \right) = Concat\left( {hea{{d}_1}, \ldots ,hea{{d}_h}} \right)}\\ {where;{{head}_i} = \ Attention\left( {{{Q}_i},\ {{K}_i},\ {{V}_i}} \right)} \end{array} \end{equation}

()

where

{{Q}_i} = \ X\ {{W}_{{{Q}_i}}}

{{K}_i} = \ X\ {{W}_{{{K}_i}}}

, and

{{V}_i} = \ X\ {{W}_{{{V}_i}}}

denote the respective subspaces defined by the weight matrices

{{W}_{{{Q}_i}}}

{{W}_{{{K}_i}}}

and

{{W}_{{{V}_i}}}

GNNs are designed to process graph-structured data. The foundational idea of GNN is to generate node or edge representations by aggregating information from neighbouring nodes. This is achieved by the message-passing function via an iterative process. Given a graph as

G\ = \ ( {V,\ E} )

, this process can be formulated as follows:

\begin{equation} \def\eqcellsep{&}\begin{array}{*{20}{c}} {\ {{h}_i} = \ \phi \left( {{{x}_i},\ {{ \oplus }_{{{v}_j}\ \in N\left( {{{v}_i}} \right)}}\ \psi \left( {{{x}_i},\ {{x}_j},\ {{e}_{ij}}} \right)} \right)} \end{array} \end{equation}

()

where

\oplus

is the permutation-invariant aggregation operator,

\phi ( \cdot )

and

\psi ( \cdot )

are typically implemented as neural networks, which aggregate information from neighbouring nodes

N( {{{v}_i}} )

3.4 Deep learning based models

In the context of employing deep learning techniques, it is essential to contemplate two principal elements: the backbone architecture of the model and the training objective that guides the learning process. Recent research has witnessed a proliferation of models utilizing backbone architectures such as FCNN, GNN, and Transformers. Regarding the training objectives, single-task learning (STL) and multi-task learning (MTL) have emerged as prevalent strategies. STL models are specifically tailored to optimize the prediction of drug combination synergy. Conversely, MTL models are trained to simultaneously achieve performance on multiple related tasks. These tasks may encompass not only the prediction of synergy but also other pertinent objectives such as drug-drug interaction classification⁵¹ and single-drug response prediction.⁵²

The selection of the backbone architecture in deep learning models is primarily influenced by the nature of the drug features and cell line representation. Specifically, when dealing with one-dimensional (1D) data such as molecular fingerprints and gene expression profiles, FCNN often emerge as the architecture of choice. DeepSynergy³⁸ is a representative model that utilizes FCNN and employs concatenated features of drug pairs and cell lines as input. Similarly, AuDNNsynergy⁵³ adopts a comparable FCNN-based network, which incorporates three autoencoders to extract latent features. Principal Component Analysis precedes the input into the FCNN to ensure that the data is represented in a lower-dimensional space, as demonstrated in SynPred.⁵⁴ KGE-DC⁵⁵ employs a three-layer FCNN to predict drug combination synergy by integrating information from knowledge graphs (KGs) about drugs and cell lines with molecular fingerprints and gene expression data. Recent models like CCSynergy⁴⁴ and SynPathy⁵⁶ also utilize FCNNs but integrate a broader range of drug and cell features to improve prediction accuracy. In contrast to the DeepSynergy architecture, which treats drug pair and cell line features as a single entity, MatchMaker³⁹ introduces a novel FCNN model that uses two subnetworks to individually model the interactions of each drug with the cell line. This design principle has been adopted by MARSY⁵² and MTLSynergy.⁵⁷ However, this architecture must satisfy the permutation invariant requirement to ensure consistent predictions regardless of the input order.

Beyond the 1D input data, drug structures and biological knowledge are also utilized as inputs in deep learning models, with GNNs being employed to model these data structures effectively. Drug structures are commonly represented as graphs, where nodes correspond to atoms and edges, represent chemical bonds. This graph representation allows for the application of various GNNs to extract features from the molecular structure, which are crucial for understanding the pharmacological properties of drugs. Studies such as DeepDDS,⁴¹ AttenSyn⁴² and GTextSyn⁵⁸ have leveraged GNNs to capture these structural features. In contrast to the representation of drug structures, some studies have attempted to design cell line-specific graphs. For instance, MGAE-DC models each cell line as three distinct graphs based on the interactions between drugs.⁵⁹ This model employs a graph encoder-decoder architecture to capture drug embeddings that are common across different cell lines. Similarly, SDCNet⁴⁰ constructs unique relational graphs for each cell line and utilizes a relational GCN to learn invariant patterns of drug combinations.

In addition to constructing individual graphs for each cell line, drug combination synergy data can be conceptualized as a graph where drugs and cell lines serve as nodes. CGMS treats this graph as a heterogeneous graph and employs the heterogeneous graph attention network to generate graph embeddings.⁴⁹ HypergraphSynergy⁴⁸ and HypertranSynergy⁵⁰ model this graph as a hypergraph and utilize different hypergraph neural networks to model the synergy prediction task. Furthermore, by incorporating external biological knowledge, early works such as GraphSynergy⁴⁶ and PRODeepSyn,⁶⁰ which utilize PPI networks to represent drug and cell line features, have shown comparable performance.

The Transformer architecture has demonstrated its effectiveness across various domains. DTSyn introduces a dual Transformer encoder framework designed to extract correlations among drugs, targets, and cell lines.⁶¹ DFFNDDS employs a pre-trained chemical language model that utilizes the Transformer as its foundational element to distil drug features from the SMILES.⁶² DeepTraSynergy also harnesses the power of Transformers as feature extractors.⁶³ SynergyX takes advantage of the Transformer's capability to model cross-modal biological knowledge.⁴³ Inspired by the success of large language models (LLMs) in natural language processing, several studies have extended the application of LLMs to the domain of drug combination synergy prediction. CancerGPT,⁶⁴ for example, utilizes LLMs to predict the synergy, demonstrating the potential of transfer learning from language models to biomedical applications. SynerGPT introduces a GPT model to learn drug synergy functions.⁶⁵

In Figure 3 , we present a detailed report on the parameter count and inference times for a selection of representative models, including DeepSynergy, DeepDDS-GAT, DeepDDS-GCN, HypergraphSynergy, DFFNDDS, SynegyX, MF- SynDCP and PermuteDDS.⁶⁶ These metrics were obtained using an Intel(R) Xeon(R) Gold 6226R CPU @ 2.90 GHz in conjunction with a GeForce RTX 3090 graphics card. It is important to note that this analysis does not encompass all existing models.

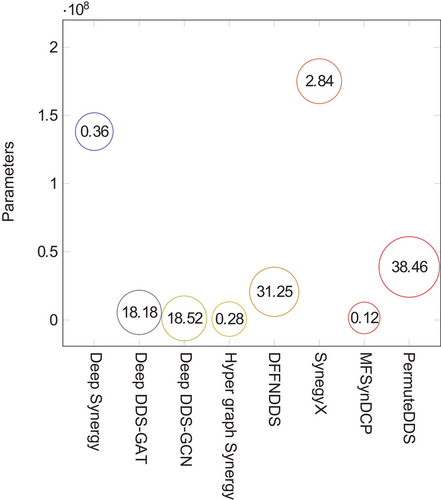
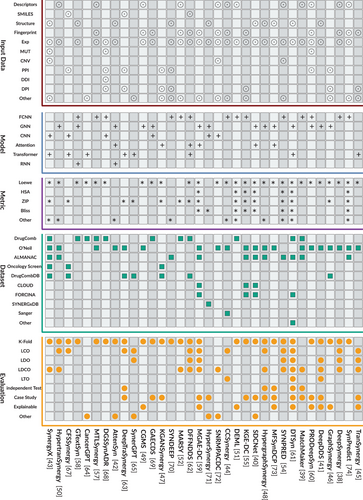
Figure 3 presents a comparative analysis of the efficiency and complexity of the aforementioned models, as measured by their parameter count and inference time, respectively. The ordinate (y-axis) delineates the parameter count for each model, with each represented as a discrete point on the graph. Adjacent to each point, the inference time is annotated, providing a direct indication of the model's operational latency when processing new data. Upon examination of the figure, it is evident that the parameter count varies substantially, extending from approximately 5.86 million parameters for the DeepDDS-GAT model to a more considerable 175 million parameters for the SynegyX model. Con- currently, the inference times exhibit a similarly broad spectrum, with the MFSynDCP model demonstrating the most expeditious performance at roughly 0.12 ms, while the PermuteDDS model exhibits the longest latency, at 38.46 ms.

3.5 Evaluation

The evaluation of model performance is a crucial step in assessing the efficacy of these models. While k-fold cross-validation (CV) techniques are commonly employed, certain studies have adopted specialized CV strategies to better simulate real-world scenarios.^67-74 These strategies include:

Leave Cell Line Out (LCO): This strategy involves excluding specific cell lines from the training data, enabling assessment of the model's performance across different diseases. LCO variants may exclude a certain percentage of specific cell lines or leave out one cell line entirely.^{48, 41}
Leave Drug Out (LDO): In this strategy, a single drug is omitted from the training dataset, allowing evaluation of the model's predictive capabilities for the excluded drug. Like LCO, LDO variants may exclude a certain percentage of specific drugs or leave out one drug entirely.
Leave Drugs Out (LDSO): Similar to LDO, LDPO extends the evaluation to drug pairs, excluding certain drug combinations from the training set to assess the model's robustness.
Leave Drug Combination Out (LDCO): This strategy involves removing specific drug combinations to evaluate the model's ability to predict the synergy of new drug combinations.
Leave Tissue Out: By excluding specific tissue types, this approach tests the model's generalizability to different biological contexts.

By simulating challenges such as predicting outcomes in new diseases or with new drugs, these specialized CV strategies better prepare models for clinical use and drug development.

In addition to CV strategies, other evaluation approaches include independent testing,^{48, 50} case studies^{39, 43} and explainable experiments.^{41, 43, 45, 46} Among these experiments, Interpretability is crucial for understanding why a model makes a particular decision. However, there are limitations in current approaches. Some studies evaluate interpretability only through examples, and evaluations often rely on visualizing attention weights⁴³ or Euclidean distances via dimensionality reduction methods,⁵⁹ lacking a unified standard for systematically assessing interpretability.

4 CHALLENGES AND FUTURE DIRECTIONS

While current deep learning-based models have demonstrated commendable performance in drug combination synergy prediction, it is essential to recognize the limitations inherent in these models. One such limitation pertains to the input features, where the majority of existing models rely on 1D and 2D information, with the 3D structural in the formation of drugs being notably underutilized. Research has indicated that the three-dimensional conformations of drugs are crucial for understanding Drug-Drug Interactions.⁷⁵

Furthermore, while trained chemical models have been employed with notable success in drug-related tasks, the specialized models such as GraphMVP,⁷⁶ MolCLR⁷⁷ and UNI-MOL⁷⁸ outperform traditional fingerprint and chemical descriptor-based approaches, as well as SMILES-derived representations. These models offer a more nuanced understanding of molecular structures and their pharmacological properties.

In addition to drug features, the representation of cell line features warrants reevaluation. It has been observed that many models exhibit subpar performance under the LCO strategy,^{49, 59, 54} which suggests a need to rethink the way cell lines are characterized within these models. The LCO strategy is particularly revealing, as it tests the model's generalised ability for real-world applications.

LLMs have demonstrated remarkable efficacy across a spectrum of natural language processing tasks. This success has catalyzed growing interest in the fields of bioinformatics and biomedicine, where researchers are integrating the sophisticated reasoning capabilities of LLMs with biomedical data.^{79, 80} Notably, initiatives like CancerGPT have begun exploring the application of LLMs for drug combination synergy prediction.⁶⁴ Concurrently, the evolution of multi-modal LLMs (MLLMs) has extended the capacity to comprehend information spanning various modalities.⁸¹^– ⁸³ Despite these advancements, the potential of MLLMs in the context of drug combination synergy prediction remains largely untapped.

AUTHOR CONTRIBUTIONS

Yu Wang did a literature search. Junjie Wang and Yun Liu conceived and designed this study. Junjie Wang oversaw the drafting and editing. All authors reviewed the manuscript.

ACKNOWLEDGEMENTS

We thank the reviewers who provided helpful comments on earlier drafts of the manuscript. This work was supported by the National Key R&D Program of China (Grant No.2023YFC3605800) and the National Natural Science Foundation of China (NSFC, Grant Nos. 62271174 and 62102191).

CONFLICT OF INTEREST STATEMENT

The authors declare no conflict of interest.

ETHICS STATEMENT

This article does not contain any studies with human participants or animals performed by any of the authors.

Open Research

DATA AVAILABILITY STATEMENT

No data are available.

REFERENCES

1Kim Y, Zheng S, Tang J, Jim Zheng W, Li Z, Jiang X. Anticancer drug synergy prediction in understudied tissues using transfer learning. J Am Med Inform Assoc 2021; 28(1): 42-51.
10.1093/jamia/ocaa212
PubMed Web of Science® Google Scholar
2Vitiello PP, Martini G, Mele L, et al. Vulnerability to low-dose combination of irinotecan and niraparib in ATM-mutated colorectal cancer. J Exp Clin Cancer Res 2021; 40: 1-15.
10.1186/s13046-020-01811-8
PubMed Web of Science® Google Scholar
3Alruwaili MM, Zonneville J, Naranjo MN, et al. A synergistic two-drug therapy specifically targets a DNA repair dysregulation that occurs in p53-deficient colorectal and pancreatic cancers. Cell Rep Med. 2024; 5(3):101434. https://www.sciencedirect.com/science/article/pii/S2666379124000570
10.1016/j.xcrm.2024.101434
CAS PubMed Google Scholar
4Neutel JM, Giles TD, Punzi H, Weiss RJ, Li H, Finck A. Long-term safety of nebivolol and valsartan combination therapy in patients with hypertension: an open-label, single-arm, multicenter study. J Am Soc Hypertension. 2014; 8(12): 915-920.
10.1016/j.jash.2014.09.017
CAS PubMed Web of Science® Google Scholar
5Giles TD, Weber MA, Basile J, et al. Efficacy and safety of nebivolol and valsartan as fixed-dose combination in hypertension: a randomised, multicentre study. Lancet North Am Ed. 2014; 383(9932): 1889-1898.
10.1016/S0140-6736(14)60614-0
CAS PubMed Web of Science® Google Scholar
6Zheng W, Sun W, Simeonov A. Drug repurposing screens and synergistic drug-combinations for infectious diseases. Br J Pharmacol 2018; 175(2): 181-191.
10.1111/bph.13895
CAS PubMed Web of Science® Google Scholar
7Guo H, Guo M, Xia Z, Shao Z. Membrane-coated nanoparticles as a biomimetic targeted delivery system for tumour therapy. Biomater Transl. 2024; 5(1): 33.
Google Scholar
8Kingsak M, Meethong T, Jongkhumkrong J, Cai L, Wang Q. Therapeutic potential of oncolytic viruses in the era of precision oncology. Biomater Transl. 2023; 4(2): 67.
PubMed Google Scholar
9Azam F, Vazquez A. Trends in phase ii trials for cancer therapies. Cancers. 2021; 13(2): 178.
10.3390/cancers13020178
CAS PubMed Web of Science® Google Scholar
10Bobrowski T, Chen L, Eastman RT, et al. Synergistic and antagonistic drug combinations against SARS-CoV-2. Mol Ther. 2021; 29(2): 873-885.
10.1016/j.ymthe.2020.12.016
CAS PubMed Web of Science® Google Scholar
11Li P, Huang C, Fu Y, et al. Large-scale exploration and analysis of drug combinations. Bioinformatics 2015: 31(12): 2007-2016.
10.1093/bioinformatics/btv080
CAS PubMed Web of Science® Google Scholar
12Li H, Li T, Quang D, Guan Y. Network propagation predicts drug synergy in cancers predict drug synergy with network propagation. Cancer Res. 2018: 78(18): 5446-5457.
10.1158/0008-5472.CAN-18-0740
CAS PubMed Web of Science® Google Scholar
13Meng F, Li F, Liu JX, Shang J, Liu X, Li Y. NEXGB: a network embedding framework for anticancer drug combination prediction. Int J Mol Sci. 2022; 23(17): 9838.
10.3390/ijms23179838
CAS PubMed Web of Science® Google Scholar
14Sidorov P, Naulaerts S, Ariey-Bonnet J, Pasquier E, Ballester PJ. Predicting synergism of cancer drug combinations using NCI-ALMANAC data. Front Chem. 2019: 7: 509.
10.3389/fchem.2019.00509
PubMed Web of Science® Google Scholar
15Öztürk H, Özgür A, Ozkirimli E. DeepDTA: deep drug–target binding affinity prediction. Bioinformatics 2018; 34(17): i821-i829.
10.1093/bioinformatics/bty593
PubMed Web of Science® Google Scholar
16Luo X. Wang L, Hu P. Hu L. Predicting Protein-Protein Interactions Using Sequence and Network lnformation via Variational Graph Autoencoder. IEEE/ACM Transactions on Computational Biology and Bioinformatics; 2023.
Google Scholar
17Li Z, Song P, Li G, et al. AI energized hydrogel design, optimization and application in biomedicine. Mater Today Bio. 2024; 25:101014.
10.1016/j.mtbio.2024.101014
CAS PubMed Google Scholar
18Bai L, Wu Y, Li G, Zhang W, Zhang H, Su J. AI-enabled organoids: construction, analysis, and application. Bioact Mater. 2024; 31: 525-548.
10.1016/j.bioactmat.2023.09.005
PubMed Web of Science® Google Scholar
19Morrone JA, Weber JK, Huynh T, Luo H, Cornell WD. Combining docking pose rank and structure with deep learning improves protein–ligand binding mode prediction over a baseline docking approach. J Chem Inf Model. 2020; 60(9): 4170-4179.
10.1021/acs.jcim.9b00927
CAS PubMed Web of Science® Google Scholar
20O'Shea K, Nash R. An introduction to convolutional neural networks. 2015.
Google Scholar
21Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. 2017.
Google Scholar
22Scarselli F, Gori M, Tsoi AC, Hagenbuchner M, Monfardini G. The graph neural network model. IEEE Trans Neural Networks. 2008; 20(1): 61-80.
10.1109/TNN.2008.2005605
PubMed Google Scholar
23Loewe S. The problem of synergism and antagonism of combined drugs. Arzneimitte-Forschung. 1953: 3(6): 285-290.
CAS PubMed Web of Science® Google Scholar
24Bliss Cl. The toxicity of poisons applied jointly 1. Ann Appl Biol 1939; 26(3): 585-615.
10.1111/j.1744-7348.1939.tb06990.x
CAS Google Scholar
25Lavigne GJ, Montplaisir JV. Bruxism: epidemiology, diagnosis, pathophysiology, and pharmacology. In: JR Fricton, R Dubner, eds. Orofacial pain and temporomandibular disorders: advances in pain research and therapy. New York: Raven Press; 1995. pp. 387-404.
Google Scholar
26Yadav B, Wennerberg K, Aittokallio T, Tang J. Searching for drug synergy in complex dose–response landscapes using an interaction potency model. Comput Struct Biotechnol J. 2015; 13: 504-513.
10.1016/j.csbj.2015.09.001
CAS PubMed Web of Science® Google Scholar
27Chou TC, Talalay P. Quantitative analysis of dose-effect relationships: the combined effects of multiple drugs or enzyme inhibitors. Adv Enzyme Regul. 1984; 22: 27-55.
10.1016/0065-2571(84)90007-4
CAS PubMed Web of Science® Google Scholar
28Malyutina A, Maiumder MM, Wang W, Pessia A, Heckman CA, Tang J. Drug combination sensitivity scoring facilitates the discovery of synergistic and efficacious drug combinations in cancer. PLoS Comput Biol. 2019; 15(5):e1006752.
10.1371/journal.pcbi.1006752
CAS PubMed Web of Science® Google Scholar
29Holbeck SL, Camalier R, Crowell JA, et al. The National Cancer Institute ALMANAC: a comprehensive screening resource for the detection of anticancer drug pairs with enhanced therapeutic activity. Cancer Res. 2017; 77(13): 3564-3576.
10.1158/0008-5472.CAN-17-0489
CAS PubMed Web of Science® Google Scholar
30Wooten DJ, Meyer CT, Lubbock AL, Quaranta V, Lopez CF. MuSyC is a consensus framework that unifies multi-drug synergy metrics for combinatorial drug discovery. Nat Commun. 2021; 12(1): 4607.
10.1038/s41467-021-24789-z
CAS PubMed Web of Science® Google Scholar
31Zhang H, Ek CH, Rattray M, Milo M. SynBa: improved estimation of drug combination synergies with uncertainty quantification. Bioinformatics. 2023; 39(Supplement_1): i121-i130.
10.1093/bioinformatics/btad240
PubMed Google Scholar
32Zheng S, Aldahdooh J, Shadbahr T, et al. DrugComb update: a more comprehensive drug sensitivity data repository and analysis portal. Nucleic Acids Res. 2021; 49(W1): W174-W184. doi:10.1093/nar/gkab438
10.1093/nar/gkab438
CAS PubMed Web of Science® Google Scholar
33O'Neil J, Benita Y, Feldman I, et al. An unbiased oncology compound screen to identify novel combination strategies. Mol Cancer Ther. 2016; 15(6): 1155-1162.
10.1158/1535-7163.MCT-15-0843
PubMed Web of Science® Google Scholar
34Liu H, Zhang W, Zou B, Wang J, Deng DL. DrugCombDB: a comprehensive database of drug combinations toward the discovery of combinatorial therapy. Nucleic Acids Res. 2020: 48(D1): D871-D881.
CAS PubMed Web of Science® Google Scholar
35Seo H, Tkachuk D, Ho C, et al. SYNERGxDB: an integrative pharmacogenomic portal to identify synergistic drug combinations for precision oncology. Nucleic Acids Res. 2020; 48(W1): W494-W501.
10.1093/nar/gkaa421
CAS PubMed Web of Science® Google Scholar
36Shtar G, Azulay L. Nizri O, Rokach L, Shapira B. CDCDB: a large and continuously updated drug combination database. Sci Data. 2022: 9(1): 263.
10.1038/s41597-022-01360-z
PubMed Web of Science® Google Scholar
37Sun X, Zhang Y, Zhou Y, et al. NPCDR: natural product-based drug combination and its disease-specific molecular regulation. Nucleic Acids Res. 2022; 50(D1): D1324-D1333.
10.1093/nar/gkab913
CAS PubMed Web of Science® Google Scholar
38Preuer K, Lewis RP, Hochreiter S, Bender A, Bulusu KC, Klambauer G. DeepSynergy: predicting anti-cancer drug synergy with deep learning. Bioinformatics. 2018; 34(9): 1538-1546.
10.1093/bioinformatics/btx806
CAS PubMed Web of Science® Google Scholar
39Kuru HL, Tastan O, Cicek AE. MatchMaker: a deep learning framework for drug synergy prediction. IEEE/ACM Trans Comput Biol Bioinf. 2021; 19(4): 2334-2344.
10.1109/TCBB.2021.3086702
Web of Science® Google Scholar
40Zhang P, Tu S, Zhang W, Xu L. Predicting cell line-specific synergistic drug combinations through a relational graph convolutional network with attention mechanism. Brief Bioinf. 2022; 23(6):bbac403.
10.1093/bib/bbac403
Web of Science® Google Scholar
41Wang J, Liu X, Shen S, Deng L, Liu H. DeepDDS: deep graph neural network with attention mechanism to predict synergistic drug combinations. Brief Bioinf. 2022; 23(1):bbab390.
10.1093/bib/bbab390
PubMed Web of Science® Google Scholar
42Wang T, Wang R, Wei L. AttenSyn: an attention-based deep graph neural network for anticancer synergistic drug combination prediction. J Chem Inf Model. 2024; 64(7) 2854-2862.
10.1021/acs.jcim.3c00709
CAS PubMed Web of Science® Google Scholar
43Guo Y, Hu H, Chen W, et al. SynergyX: a multi-modality mutual attention network for interpretable drug synergy prediction. Brief Bioinf. 2024: 25(2):bbae015. doi:10.1093/bib/bbae015
10.1093/bib/bbae015
PubMed Web of Science® Google Scholar
44Hosseini SR, Zhou X. CCSynergy: an integrative deep-learning framework enabling context-aware prediction of anti-cancer drug synergy. Brief Bioinf. 2023; 24(1):bbac588.
10.1093/bib/bbac588
PubMed Web of Science® Google Scholar
45Liu Q, Xie L. TranSynergy: mechanism-driven interpretable deep neural network for the synergistic prediction and pathway deconvolution of drug combinations. PLoS Comput Biol. 2021; 17(2):e1008653.
10.1371/journal.pcbi.1008653
CAS PubMed Web of Science® Google Scholar
46Yang J, Xu Z, Wu WKK, Chu Q, Zhang Q. GraphSynergy: a network-inspired deep learning model for anticancer drug combination prediction. J Am Med Inform Assoc. 2021; 28(11): 2336-2345.
10.1093/jamia/ocab162
PubMed Web of Science® Google Scholar
47Zhang G, Gao Z, Yan C, et al. KGANSynergy: knowledge graph attention network for drug synergy prediction. Brief Bioinf. 2023; 24(3):bbad167.
10.1093/bib/bbad167
PubMed Web of Science® Google Scholar
48Liu X, Song C, Liu S, Li M, Zhou X, Zhang W. Multi-way relation-enhanced hypergraph representation learning for anti-cancer drug synergy prediction. Bioinformatics. 2022; 38(20): 4782-4789.
10.1093/bioinformatics/btac579
CAS PubMed Web of Science® Google Scholar
49Wang X, Zhu H, Chen D, Yu Y, Liu Q, Liu Q. A complete graph-based approach with multi-task learning for predicting synergistic drug combinations. Bioinformatics. 2023; 39(6):btad351.
10.1093/bioinformatics/btad351
CAS PubMed Web of Science® Google Scholar
50Wang W, Yuan G, Wan S, et al. A granularity-level information fusion strategy on hypergraphtransformer for predicting synergistic effects of anticancer drugs. Brief Bioinf. 2024: 25(1):bbad522.
10.1093/bib/bbad522
Web of Science® Google Scholar
51Wang Z, Dong J, Wu L, et al. DEML: drug synergy and interaction prediction using ensemble-based multi-task learning. Molecules. 2023; 28(2): 844.
10.3390/molecules28020844
CAS PubMed Web of Science® Google Scholar
52El Khili MR, Memon SA, Emad A. MARSY: a multitask deep-learning framework for prediction of drug combination synergy scores. Bioinformatics. 2023; 39(4):btad177.
10.1093/bioinformatics/btad177
CAS PubMed Web of Science® Google Scholar
53Zhang T, Zhang L, Payne PR, Li F. Synergistic drug combination prediction by integrating multiomics data in deep learningmodels. Methods Mol Biol. 2021; 2194: 223-238.
10.1007/978-1-0716-0849-4_12
CAS PubMed Google Scholar
54Preto AJ, Matos-Filipe P, Mourão J, Moreira IS. SYNPRED: prediction of drug combination effects in cancer using different synergy metrics and ensemble learning. GigaScience. 2022; 11:giac087.
10.1093/gigascience/giac087
PubMed Web of Science® Google Scholar
55Zhang P. Tu S. A knowledge graph embedding-based method for predicting the synergistic effects of drug combinations. In: 2022 IEEE International Conference on Bioinformatics and Biomedicine (BIBM) IEEE: 2022. pp. 1974-1981.
Google Scholar
56Tang YC, Gottlieb A. SynPathy: predicting drug synergy through drug-associated pathways using deep learning. Mol Cancer Res. 2022; 20(5): 762-769.
10.1158/1541-7786.MCR-21-0735
CAS PubMed Web of Science® Google Scholar
57Chen D, Wang X, Zhu H, et al. Predicting anticancer synergistic drug combinations based on multi-task learning. BMC Bioinf. 2023: 24(1): 448.
10.1186/s12859-023-05524-5
PubMed Web of Science® Google Scholar
58Yan S, Zheng D. A deep neural network for predicting synergistic drug combinations on cancer. Interdiscip Sci. 2024; 16(1): 218-230.
10.1007/s12539-023-00596-6
PubMed Web of Science® Google Scholar
59Zhang P, Tu S. MGAE-DC: predicting the synergistic effects of drug combinations through multi-channel graph autoencoders. PLoS Comput Biol. 2023; 19(3)e1010951.
10.1371/journal.pcbi.1010951
CAS PubMed Web of Science® Google Scholar
60Wang X, Zhu H, Jiang Y, et al. PRODeepSyn: predicting anticancer synergistic drug combinations by embedding cell lines with protein–protein interaction network. Brief Bioinf. 2022; 23(2):bbab587.
10.1093/bib/bbab587
PubMed Web of Science® Google Scholar
61Hu J, Gao J, Fang X, et al. DTSyn: a dual-transformer-based neural network to predict synergistic drug combinations. Brief Bioinf. 2022: 23(5):bbac302.
10.1093/bib/bbac302
PubMed Web of Science® Google Scholar
62Xu M, Zhao X, Wang J, et al. DFFNDDS: prediction of synergistic drug combinations with dual feature fusion networks. J Cheminform. 2023: 15(1): 33.
10.1186/s13321-023-00690-3
PubMed Web of Science® Google Scholar
63Rafiei F, Zeraati H, Abbasi K, Ghasemi JB, Parsaeian M, Masoudi-Nejad A. DeepTraSynergy: drug combinations using multimodal deep learning with transformers. Bioinformatics. 2023; 39(8):btad438.
10.1093/bioinformatics/btad438
CAS PubMed Web of Science® Google Scholar
64Li T, Shetty S, Kamath A, et al. CancerGPT for few shot drug pair synergy prediction using large pretrained language models. NPJ Digital Med. 2024; 7(1): 40.
10.1038/s41746-024-01024-9
PubMed Web of Science® Google Scholar
65Edwards CN, Naik A, Khot T, Burke MD, Ji H, Hope T. SynerGPT: in-context learning for personalized drug synergy prediction and drug design. Biorxiv. 2023;p. 2007-2023.
Google Scholar
66Zhao X, Xu J, Shui Y, et al, PermuteDDS: a permutable feature fusion network for drug-drug synergyprediction. J Cheminform. 2024; 16(1): 41.
10.1186/s13321-024-00839-8
PubMed Web of Science® Google Scholar
67Rafiei F, Zeraati H, Abbasi K, et al. CFSSynergy: combining feature-based and similarity-based methods for drug synergy prediction. J Chem Inf Model. 2024.
10.1021/acs.jcim.3c01486
PubMed Web of Science® Google Scholar
68Gan Y, Huang X, Guo W, Yan C, Zou G. Predicting synergistic anticancer drug combination based on low-rank global attention mechanism and bilinear predictor. Bioinformatics. 2023; 39(10):btad607.
10.1093/bioinformatics/btad607
CAS PubMed Web of Science® Google Scholar
69Li H, Zou L, Kowah JA, et al. Predicting drug synergy and discovering new drug combinations based on a graph autoencoder and convolutional neural network. Interdiscipl Sci. 2023; 15(2): 316-330.
10.1007/s12539-023-00558-y
PubMed Web of Science® Google Scholar
70Torkamannia A, Omidi Y, Ferdousi R. SYNDEEP: a deep learning approach for the prediction of cancer drugs synergy. Sci Rep. 2023; 13(1): 6184.
10.1038/s41598-023-33271-3
CAS PubMed Google Scholar
71Zhang Q, Zhang S, Feng Y, Shi J. Few-shot drug synergy prediction with a prior-guided hypernetwork architecture. IEEE Trans Pattern Anal Mach Intell. 2023; 45(8): 9709-9725.
10.1109/TPAMI.2023.3248041
PubMed Web of Science® Google Scholar
72Li TH, Wang CC, Zhang L, Chen X. SNRMPACDC: computational model focused on Siamese network and random matrixprojection for anticancer synergistic drug combination prediction. Brief Bioinf. 2023: 24(1):bbac503.
10.1093/bib/bbac503
PubMed Web of Science® Google Scholar
73Dong Y, Chang Y, Wang Y, et al. MFSynDCP: multi-source feature collaborative interactive learning for drug combination synergy prediction. BMC Bioinf. 2024; 25(1): 140.
10.1186/s12859-024-05765-y
PubMed Web of Science® Google Scholar
74Alsherbiny MA, Radwan I, Moustafa N, et al. Trustworthy deep neural network for inferring anticancer synergistic combinations. IEEE J Biomed Health Inf. 2021; 27(4): 1691-1700.
10.1109/JBHI.2021.3126339
Web of Science® Google Scholar
75He H, Chen G, Yu-Chian Chen C. 3DGT-DDI: 3D graph and text based neural network for drug–drug interaction pre- diction. Brief Bioinf. 2022; 23(3):bbac134.
10.1093/bib/bbac134
PubMed Web of Science® Google Scholar
76Liu S, Wang H, Liu W, Lasenby J, Guo H, Tang J. Pre-training molecular graph representation with 3D geometry. In: The Tenth International Conference on Learning Representations, ICLR 2022, Virtual Event, April 25–29.
Google Scholar
77Wang Y, Wang J, Cao Z, Barati Farimani A. Molecular contrastive learning of representations via graph neural networks. Nat Machine Intell. 2022: 4(3): 279-287.
10.1038/s42256-022-00447-x
Google Scholar
78Zhou G, Gao Z, Ding Q, et al. Uni-Mol: a universal 3D molecular representation learning framework. In: The Eleventh International Conference on Learning Representations, ICLR 2023, Kigali, Rwanda, May 1–5.
Google Scholar
79Thirunavukarasu AJ, Ting DS, Elangovan K, Gutierrez L, Tan TF, Ting DSW. Large language models in medicine. Nat Med. 2023: 29(8): 1930-1940.
10.1038/s41591-023-02448-8
CAS PubMed Web of Science® Google Scholar
80Schubert MC. Wick W. Venkataramani V. Performance of large language models on a neurology board-style examination. JAMA Netw Open. 2023: 6(12):e2346721.
10.1001/jamanetworkopen.2023.46721
PubMed Web of Science® Google Scholar
81Ma K, Zang X, Feng Z, et al. LLaViLo: boosting video moment retrieval via adapter-based multimodal modeling. In: Proceedings of the IEEE/CVF International Conference on Computer Vision; 2023. p. 2798-2803.
Google Scholar
82Xu H, Ye Q, Yan M, et al. mPLUG-2: a modularized multi-modal foundation model across text, image and video. In: A Krause, E Brunskill, K Cho, B Engelhardt, S Sabato, J Scarlett, eds. International Conference on Machine Learning, ICML 2023, 23–29 July 2023, Honolulu, Hawaii, USA, vol. 202 of Proceedings of Machine Learning Research PMLR; 2023. pp. 38728-38748. https://proceedings.mlr.press/v202/xu23s.html
Google Scholar
83Li J, Li D, Savarese S, Hoi SCH. BLIP-2: bootstrapping language-image pre-training with frozen image encoders and large language models. In: A Krause, E Brunskill, K Cho, B Engelhardt, S Sabato, J Scarlett, eds. International Conference on Machine Learning, ICML 2023, 23–29 July 2023, Honolulu, Hawaii, USA, vol. 202 of Proceedings of Machine Learning Research PMLR; 2023. pp. 19730-19742. https://proceedings.mlr.press/v202/li23q.html
Google Scholar

Volume4, Issue3

June 2024

e317

Deep learning for predicting synergistic drug combinations: State-of-the-arts and future directions

Abstract

1 INTRODUCTION

2 METRICS OF SYNERGISTIC EFFECT IN DRUG COMBINATIONS PREDICTION TASK