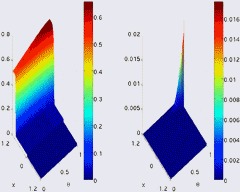
The continuous sedimentation process in a clarifier-thickener can be described by a scalar nonlinear conservation law for the local solids volume fraction. The flux density function is discontinuous with respect to spatial position due to feed and discharge mechanisms. Typically, the feed flow cannot be given deterministically and efficient numerical simulation requires a concept for quantifying uncertainty. In this paper uncertainty quantification is expressed by a new hybrid stochastic Galerkin (HSG) method that extends the classical polynomial chaos approximation by multiresolution discretization in the stochastic space.

The analysis of problem of joined elastic beams is presented in comparison with the engineering and asymptotic approaches. The analysis is based on three-dimensional elasticity theory model and recently developed method of local perturbation [Gaudiello and Kolpakov, Int. J. Eng. Sci. 49, 295–309 (2011)], which seems to be an effective tool for analysis of fields in the vicinity of joint. Due to the strong localization of perturbation of solution, computation of local strains and stresses in the vicinity of joint can be realized with standard FEM software.

Considering crack surface friction and using complex stress function theory, the exact analytical solution of stress intensity factors (SIFs) for an infinite plane containing three collinear cracks is obtained. The effects of confining stresses, crack distances and the crack surface frictions on SIFs are analyzed through the theoretical results and the Abaqus code. A photoelastic experiment was conducted to validate the theoretical result about the effect of confining stresses.

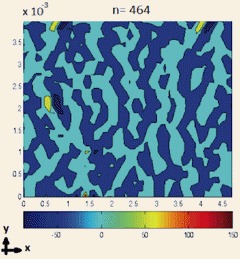
Lattice models are powerful tools to investigate damage processes in quasi-brittle material by a microscale perspective. This paper explores the connection between the series of critical strains at which the microcracks form (i.e. lattice links fail) and the second gradient of the microscale displacement field. Note worthy, the results support the new view that the damage evolution is a three regimes process (I dilute damage, II homogeneous interaction, III localization.) The featured connection with the second gradient of the microscale displacement field is applicable in regions II–III, where microcracks interactions grow stronger and the lattice transitions to the softening regime.