Journal list menu
Export Citations
Download PDFs
ISSUE INFORMATION
RESEARCH ARTICLE
Development of a new solver for homogenous mixture based on regularized gas dynamic equation system
- Pages: 1-19
- First Published: 06 September 2024
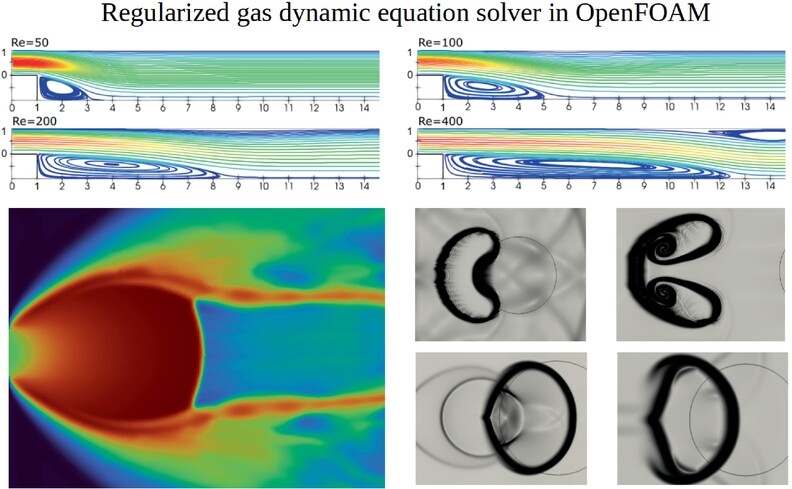
The paper presents an improved approach for modelling multi-component gas mixtures based on quasi-gasdynamic equations. The proposed numerical algorithm is implemented as a reactingQGDFoam solver based on the open-source OpenFOAM platform. This solver has been extensively validated and verified through a variety of well-described test problems. The stability and convergence parameters of the proposed numerical algorithm are determined. The simulation results are found to be in agreement with analytical solutions and experimental data.
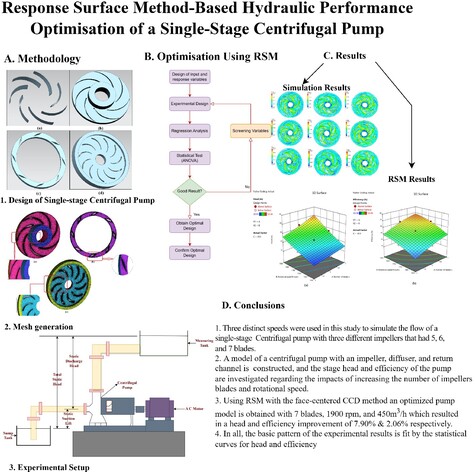
Response surface method-based hydraulic performance optimization of a single-stage centrifugal pump
- Pages: 20-43
- First Published: 07 September 2024
Turbulence effects in the topology optimization of compressible subsonic flow
- Pages: 44-68
- First Published: 16 September 2024

This paper highlights the impact and importance of including turbulence effects on topology optimization of compressible flow. The study proposes a novel approach based on Favre-Averaged Navier–Stokes equations and the compressible version of the Spalart–Allmaras model and solves first the compressible turbulent adjoint model by coupling dolphin adjoint from FEniCS and OpenFOAM software. Examples demonstrate the effects of turbulence on compressible flow and analyze industrial cases such as pipes, diffusers and mixers chambers where non-intuitive and efficient designs are presented.
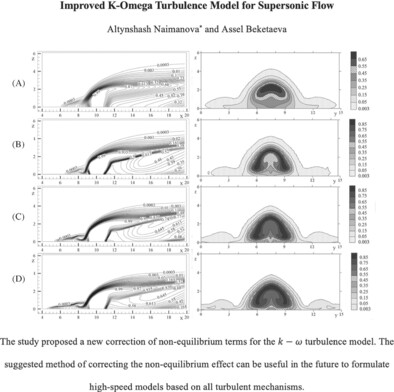
A new non-equilibrium modification of the turbulence model for supersonic turbulent flows with transverse jet
- Pages: 69-87
- First Published: 17 September 2024
Semi-implicit Lagrangian Voronoi approximation for the incompressible Navier–Stokes equations
- Pages: 88-115
- First Published: 17 September 2024
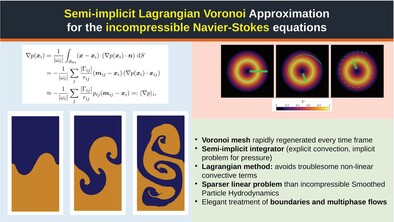
We introduce semi-implicit Lagrangian Voronoi approximation (SILVA), a novel numerical method for the solution of the incompressible Euler and Navier–Stokes equations, which combines semi-implicit time marching with time-dependent Voronoi tessellations with topology changes. In SILVA, the numerical solution is stored at particles, which move with the fluid velocity and play the role of the generators of the computational mesh. The velocity field is projected onto a divergence-free manifold. We validate SILVA by illustrative benchmarks, including viscous, inviscid, and multiphase flows.