The cover image, by Thomas-Peter Fries, is based on the Research Article Higher-order surface FEM for incompressible Navier-Stokes flows on manifolds, https://doi.org/10.1002/fld.4510.

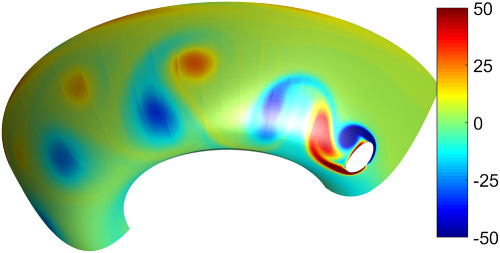
The higher-order surface FEM is used for the approximation of (in)stationary (Navier-)Stokes flows on curved manifolds. Streamline-upwind stabilization is used at high Reynolds numbers. Benchmark test cases for flows on manifolds are proposed, solutions are presented, and higher-order convergence rates are confirmed.

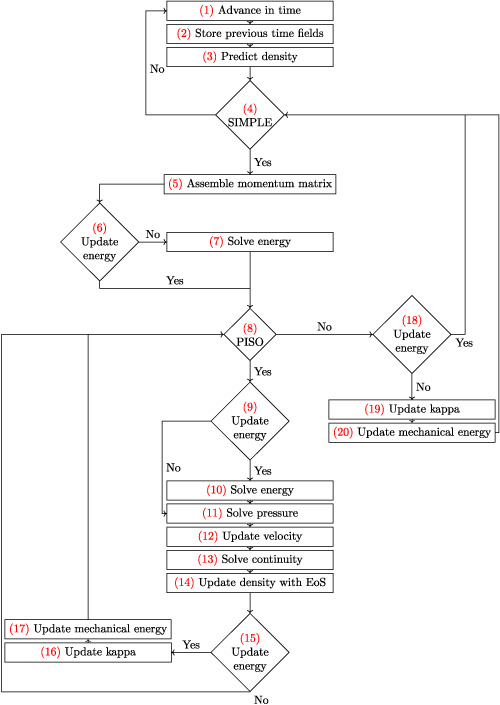
This work is an extension of a previously developed hybrid solver including arbitrary equations of state to account for nonlinear fluid behavior. Numerous test cases are described and considered showing the author a detailed overview of its capabilities. Moreover, the solver is suitable to work also with nonorthogonal meshes of varying types (hexahedral, quadrilateral, tetrahedral, triangular), making it relevant for industry applications.

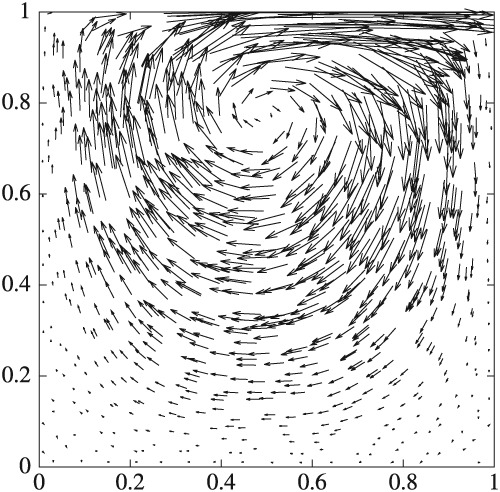
Galerkin local maximum entropy method by Nils-Arne Dreier*, Christian Engwer, Dirk Hartmann. We reinterpret the OTM by Li, Habbal, and Ortiz in the context of Galerkin discretization. This enables us to introduce constraints, like incompressibility, and stabilization terms. Ultimately, this allows the use of larger time steps and thus faster simulation. Furthermore, we provide results of numerical tests, which approve the robustness of the method.