ORIGINAL PAPER
On the bifurcation results for fractional Laplace equations
G. Dwivedi,
J. Tyagi,
R. B. Verma,
G. Dwivedi
Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar, Gujarat, 382355 India
Search for more papers by this authorCorresponding Author
J. Tyagi
Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar, Gujarat, 382355 India
Corresponding author:
email: [email protected]
Search for more papers by this authorR. B. Verma
Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar, Gujarat, 382355 India
Search for more papers by this authorG. Dwivedi,
J. Tyagi,
R. B. Verma,
G. Dwivedi
Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar, Gujarat, 382355 India
Search for more papers by this authorCorresponding Author
J. Tyagi
Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar, Gujarat, 382355 India
Corresponding author:
email: [email protected]
Search for more papers by this authorR. B. Verma
Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar, Gujarat, 382355 India
Search for more papers by this authorAbstract
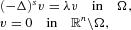
In this paper, we consider the bifurcation problem for the fractional Laplace equation
is an open bounded subset with smooth boundary, 
stands for the fractional Laplacian. We show that a continuum of solutions bifurcates out from the principal eigenvalue λ1 of the problem
References
- 1D. Applebaum, Lévy processes-from probability to finance and quantum groups, Notices Amer. Math. Soc. 51, 1336–1347 (2004).
- 2D. A. Benson, S. W. Wheatcraft, and M. M. Meerschaert, Application of a fractional advection-dispersion equation, Water Resources Res. 36, 1403–1412 (2000).
- 3J. Bertoin, Lévy Processes, Cambridge Tracts in Mathematics Vol. 121 (Cambridge Univ. Press, Cambridge, 1996).
- 4G. M. Bisci and R. Servadei, A bifurcation result for nonlocal fractional equations, Anal. Appl. 13(4), 371–394 (2015).
- 5J. Busca, Maria J. Esteban, and A. Quaas, Nonlinear eigenvalues and bifurcation problems for Pucci's operators, Ann. I. H. Poincaré 22, 187–206 (2005).
- 6X. Cabré and Y. Sire, Nonlinear equations for fractional Laplacians, I: Regularity, maximum principles, and Hamiltonian estimates, Ann. I. H. Poincaré 31, 23–53 (2014).
- 7L. Caffarelli, J. M. Roquejoffre, and Y. Sire, Variational problems for free boundaries for the fractional Laplacian, J. Eur. Math. Soc. (JEMS) 12, 1151–1179 (2010).
- 8L. Caffarelli, S. Salsa, and L. Silvestre, Regularity estimates for the solution and the free boundary of the obstacle problem for the fractional Laplacian, Invent. Math. 171, 425–461 (2008).
- 9L. Caffarelli and L. Silvestre, An extension problem related to the fractional Laplacian, Comm. Partial Differential Equations 32, 1245–1260 (2007).
- 10A. Capella, J. Dávila, L. Dupaigne, and Y. Sire, Regularity of radial extremal solutions for some non-local semilinear equations, Comm. Partial Differential Equations 36(8), 1353–1384 (2011).
- 11S. Y. A. Chang and M. González, Fractional Laplacian in conformal geometry, Adv. Math. 226, 1410–1432 (2011).
- 12M. A. Del Pino and R. Manásevich, Global bifurcation from the eigenvalues of the p-Laplacian, J. Differential Equations 92, 226–251 (1991).
- 13E. Di Nezza, G. Palatucci, and E. Valdinoci, Hitchhiker's guide to the fractional Sobolev spaces, Bull. Sci. Math. 136(5), 521–573 (2012).
- 14S. Dipierro, L. Caffarelli, and E. Valdinoci, A logistic equation with nonlocal interactions, Kinet. Relat. Models 10(1), 141–170 (2017).
- 15S. Dipierro, G. Palatucci, and E. Valdinoci, Dislocation dynamics in crystals: a macroscopic theory in a fractional Laplace setting, Comm. Math. Phys. 333(2), 1061–1105 (2015).
- 16S. Dipierro, M. Medina, I. Peral, and E. Valdinoci, Bifurcation results for a fractional elliptic equation with critical exponent in
, Manuscripta Math. (2016), DOI: 10.1007/s00229-016-0878-3.
- 17S. Dipierro, O. Savin, and E. Valdinoci, A nonlocal free boundary problem, SIAM J. Math. Anal. 47(6), 4559–4605 (2015).
- 18P. Drábek, On the global bifurcation for a class of degenerate equations, Ann. Mat. Pura Appl. 159, 1–16 (1991).
- 19P. Drábek, Solvability and Bifurcations of Nonlinear Equations, Pitman Research Notes in Mathematics Vol. 264 (Longman, Harlow, 1992).
- 20P. Drábek and Y. X. Huang, Bifurcation problems for the p-Laplacian in
, Trans. Amer. Math. Soc. 349(1), 171–188 (1997).
- 21Maria J. Esteban, P. Felmer, and A. Quaas, Eigenvalues for radially symmetric fully nonlinear operators, Comm. Partial Differential Equations 35(9), 1716–1737 (2010).
- 22A. Garroni and S. Müller, Γ-limit of a phase-field model of dislocations, SIAM J. Math. Anal. 36, 1943–1964 (2005).
- 23R. Musina and A. I. Nazarov, On fractional Laplacians, Comm. Partial Differential Equations 39(9), 1780–1790 (2014).
- 24K. Perera, M. Squassina, and Y. Yang, Bifurcation and multiplicity results for critical fractional p-laplacian problems, Math. Nachr. 289(2-3), 332–342 (2016).
- 25P. H. Rabinowitz, Some global results for nonlinear eigenvalue problems, J. Funct. Anal. 7, 487–513 (1971).
10.1016/0022-1236(71)90030-9 Google Scholar
- 26P. H. Rabinowitz, Some aspect of nonlinear eigenvalue problem, Rocky Mountain J. Math. 74, 161–202 (1973).
10.1216/RMJ-1973-3-2-161 Google Scholar
- 27X. Ros-Oton and J. Serra, The extremal solution for the fractional Laplacian, Calc. Var. Partial Differential Equations 50, 723–750 (2014).
- 28A. J. Rumbos and A. L. Edelson, Bifurcation properties of semilinear elliptic equations in
, Differential Integral Equations 7(2), 399–410 (1994).
- 29M. Saxton, Anomalous subdiffusion in fluorescence photobleaching recovery: A Monte Carlo study, J. Biophys. 81, 2226–2240 (2001).
- 30R. Servadei and E. Valdinoci, Mountain pass solutions for non-local elliptic operators, J. Math. Anal. Appl. 389(2), 887–898 (2012).
- 31R. Servadei and E. Valdinoci, On the spectrum of two different fractional operators, Proc. Roy. Soc. Edinburgh Sect A 144(4), 831–855 (2014).
- 32R. Servadei and E. Valdinoci, Weak and viscosity solutions of the fractional Laplace equations, Publ. Mat. 58(1), 133–154 (2014).
- 33L. Silvestre, Regularity of the obstacle problem for a fractional power of the Laplace operator, Comm. Pure Appl. Math. 60(1), 67–112 (2007).
- 34Y. Sire and E. Valdinoci, Fractional Laplacian phase transitions and boundary reactions: a geometric inequality and a symmetry result, J. Funct. Anal. 256(6), 1842–1864 (2009).
- 35I. V. Skrypnik, Methods for Analysis of Nonlinear Elliptic Boundary Value Problems Vol. 139 Translations of Mathematical Monographs (American Mathematical Society, 1994).
- 36J. Tan, The Brezis–Nirenberg type problem involving the square root of the Laplacian, Calc. Var. Partial Differential Equations 42(1-2), 21–41 (2011).
- 37J. Tan, Y. Wang, and J. Yang, Nonlinear fractional field equations, Nonlinear Anal. 75(4), 2098–2110 (2012).
- 38J. L. Vázquez, Recent progress in the theory of nonlinear diffusion with fractional Laplacian operators, Discrete Contin. Dyn. Syst. Ser. S 7(4), 857–885 (2014).
