Volume 2025, Issue 1 7656300

Research Article

Open Access

ACOCMPMI: An Ant Colony Optimization Algorithm Based on Composite Multiscale Part Mutual Information for Detecting Epistatic Interactions

Yan Sun,

Corresponding Author

Yan Sun

[email protected]

orcid.org/0000-0001-8422-5730

College of Engineering , Qufu Normal University , Rizhao , Shandong , China , qfnu.edu.cn

Search for more papers by this author

Jing Wang,

Jing Wang

School of Computer Science , Qufu Normal University , Rizhao , Shandong , China , qfnu.edu.cn

Search for more papers by this author

Yaxuan Zhang,

Yaxuan Zhang

School of Computer Science , Qufu Normal University , Rizhao , Shandong , China , qfnu.edu.cn

Search for more papers by this author

Junliang Shang,

Junliang Shang

orcid.org/0000-0002-8488-2228

School of Computer Science , Qufu Normal University , Rizhao , Shandong , China , qfnu.edu.cn

Search for more papers by this author

Jin-Xing Liu,

Jin-Xing Liu

School of Health and Life Science , University of Health and Rehabilitation Sciences , Qingdao , Shandong , China

Search for more papers by this author

Yan Sun,

Corresponding Author

Yan Sun

[email protected]

orcid.org/0000-0001-8422-5730

College of Engineering , Qufu Normal University , Rizhao , Shandong , China , qfnu.edu.cn

Search for more papers by this author

Jing Wang,

Jing Wang

School of Computer Science , Qufu Normal University , Rizhao , Shandong , China , qfnu.edu.cn

Search for more papers by this author

Yaxuan Zhang,

Yaxuan Zhang

School of Computer Science , Qufu Normal University , Rizhao , Shandong , China , qfnu.edu.cn

Search for more papers by this author

Junliang Shang,

Junliang Shang

orcid.org/0000-0002-8488-2228

School of Computer Science , Qufu Normal University , Rizhao , Shandong , China , qfnu.edu.cn

Search for more papers by this author

Jin-Xing Liu,

Jin-Xing Liu

School of Health and Life Science , University of Health and Rehabilitation Sciences , Qingdao , Shandong , China

Search for more papers by this author

First published: 13 June 2025

https://doi.org/10.1155/humu/7656300

Academic Editor: Priya Gusain

Share a link

Email
Wechat
Bluesky

Abstract

Epistatic interaction detection plays a pivotal role in understanding the genetic mechanisms underlying complex diseases. The effectiveness of epistatic interaction detection methods primarily depends on their interaction quantification measures and search strategies. In this study, a two-stage ant colony optimization algorithm based on composite multiscale part mutual information (ACOCMPMI) is proposed for detecting epistatic interactions. In the first stage, composite multiscale part mutual information is developed to quantify epistatic interactions, and an improved ant colony optimization algorithm incorporating filter and memory strategies is employed to search for potential epistatic interactions. In the second stage, an exhaustive search strategy and a Bayesian network score are adopted to further identify epistatic interactions within the candidate SNP set obtained in the first stage. ACOCMPMI is compared with five state-of-the-art methods, including epiACO, FDHE-IW, AntEpiSeeker, SIPSO, and MACOED, using simulation data generated from 11 epistatic interaction models. Furthermore, ACOCMPMI is applied to detect epistatic interactions in a real dataset of age-related macular degeneration. The experimental results show that ACOCMPMI is a promising method for epistatic interaction detection.

1. Introduction

In recent years, numerous single nucleotide polymorphisms (SNPs) associated with complex diseases have been successfully detected through genome-wide association studies (GWAS) [1]. However, the explanatory power of individual SNPs is limited in some complex diseases, such as cancer [2] and Alzheimer’s disease [3]. Epistatic interactions, broadly defined as nonlinear interactions between SNPs, have emerged as a key mechanism to overcome these limitations. Therefore, the precise detection of epistatic interactions has become a focal point of research [4–6].

Epistatic interaction detection focuses on two key aspects: interaction quantification measures and search strategies. Interaction can be likened to a specific type of association, predominantly manifesting as nonlinear direct associations. Quantifying these interactions relies on various association measures. Traditional statistical measures, such as logistic regression [7, 8], chi-square statistic [9], distance covariance [10], and Pearson’s correlation coefficient [11], are limited to quantifying nonlinear direct associations among target variables. Measures based on information entropy, which do not strictly depend on specific association forms, have gained significant attention in recent years. The mutual information (MI) and conditional mutual information (CMI) are commonly employed for quantifying nonlinear interactions among variables [12–15]. However, they may lead to overestimation and underestimation problems [16]. To precisely quantify nonlinear direct interactions, several measures have emerged, including maximum information coefficient (MIC) [17], conditional mutual inclusive information (CMI2) [18], part mutual information (PMI) [16], partial association (PA) [19] and multiscale part mutual information (MPMI) [20]. Notably, MPMI demonstrates higher accuracy compared with other measures and has not been applied to SNP data. Therefore, this study adopts MPMI and its variant to quantify interaction between SNPs.

The search strategy can be broadly categorized into three groups: exhaustive search, stochastic search, and heuristic search. Exhaustive search methods typically attempt to evaluate all possible SNP combinations within a dataset. However, the high dimensionality of GWAS data imposes a heavy computational burden on exhaustive methods [21]. Stochastic search methods are limited in the number of features they can handle [22]. Heuristic search transforms the epistatic interaction detection problem into an optimization problem. Heuristic search mainly focuses on metaheuristic optimization algorithms, such as the firefly algorithm [23], tree seed algorithm [24], tunicate swarm algorithm [25], side-blotched lizard algorithm [26], African vultures optimization algorithm (AVOA) [27], ant colony optimization (ACO) algorithm [28], symbiotic organisms search algorithm [29], spotted hyena optimizer algorithm [30], yellow saddle goatfish behavior optimization model [31], and grey wolf optimizer [32]. In this study, the ACO algorithm (ACO∗) is employed for searching epistatic interactions, and an improved version of the ACO∗ is presented. The ACO∗ has been widely used in this field [33] and is considered one of the most promising methods among these metaheuristic optimization algorithms.

The main contributions of this work are as follows.

•
A composite version of MPMI, termed CMPMI, is proposed. CMPMI is specifically designed for detecting nonlinear direct interactions in SNP datasets.
•
Memory and filtering strategies are integrated into the ACO∗ to improve the accuracy of epistatic interaction detection.
•
Epistatic interactions are detected in a two-stage framework. In the first stage, an improved ACO∗ combined with CMPMI is used to generate a candidate SNP set. In the second stage, an exhaustive search strategy and a Bayesian network (BN) score are adopted to further identify epistatic interactions within the candidate set.

2. Related Works

Various methods have been proposed to detect epistatic interactions. For instance, multifactor dimensionality reduction (MDR) [34], backward genotype-trait association (BGTA) [35], Boolean operation-based screening and testing (BOOST) [8], factored spectrally transformed linear mixed models (FaST-LMM) [36], and tree-based epistasis association mapping (TEAM) [37] are epistatic interaction detection methods based on exhaustive search strategies. Bayesian epistasis association mapping (BEAM) [22] and epistatic module detection (EpiMODE) [38] employ stochastic search strategies. BEAM integrates the Bayesian partitioning model with Markov chain Monte Carlo to assess and identify disease-associated SNPs and epistatic interactions. EpiMODE utilizes a Bayesian marker partition model alongside a Gibbs sampling strategy to detect epistatic interactions. For heuristic search methods, CINOEDV is designed to detect and visualize epistatic interactions of various orders, leveraging the particle swarm optimization algorithm and co-information measure [39]. AntEpiSeeker uses a two-stage ACO∗ for identifying epistatic interactions in large datasets [40]. Similarly, MACOED is a multiobjective ACO supervised heuristic method for epistasis detection [41], and IACO applies an improved ACO∗ to search for epistatic interactions [42]. MTHSA-DHEI is proposed for detecting high-order epistatic interactions based on a multitasking harmony search algorithm [43]. Building on this framework, MTHS-EE-DHEI is introduced as an enhanced variant that incorporates explicit encoding into the multitasking harmony search algorithm to further optimize the epistasis detection [44].

3. Materials and Methods

3.1. MPMI

MPMI is an innovative measure designed to quantify direct associations between target variables [20]. Unlike traditional measures, it is not confined to specific interaction forms during quantification. Furthermore, its higher accuracy and superior statistical power render it a significant advancement in this field. The MPMI between X and Y given Z is defined as

()

where both X and Z represent SNPs and Y represents the phenotype. x and z are genotypes of SNPs X and Z, and y is the class label of Y. MI(X; Z) is the MI between X and Z, and MI(Y; Z) is the MI between Y and Z. Both of them are defined as

()

where p(x, z) is the joint probability distribution of x and z, p(y, z) is the joint probability distribution of y and z, and CMI(X; Y|Z) is the CMI between X and Y given Z, which is defined as

()

where p(x, y, z) is the joint probability distribution of x, y, and z.

In addition, both D(p(x|z)‖p^∗(x|z)) and D(p(y|z)‖p^∗(y|z)) are the extended Kullback–Leibler divergences [16]. They are defined as

()

where p(x|z) and p(y|z) are the probability distributions of x and y conditioned on z, respectively, and p(x|z, y) is the probability distribution of x conditioned on both z and y.

3.2. ACO∗

The ACO∗ is a classical swarm intelligence optimization algorithm designed to solve complex combinatorial optimization problems by simulating the cooperative behavior of ant colonies [45]. The basic idea of the ACO∗ is to map feasible solutions of optimization problems to paths traversed by ants. Ants tend to release more pheromones along shorter paths during their traversal. Meanwhile, pheromones guide ants in selecting subsequent paths. Ultimately, through positive feedback, all ants converge on the optimal path, which corresponds to the optimal solution of the optimization problem. The basic ACO∗ primarily involves two core strategies: path selection and pheromone update.

Ants navigate paths based on a combination of pheromones and heuristic information. Typically, the probability of an ant selecting the next position from a given current position during an iteration is defined as

()

where τ_ij(t) is the pheromone of path i⟶j in iteration t. Similarly, η_ij represents the heuristic information of path i⟶j. α and β are the weight coefficients of pheromone and heuristic information, respectively, both of which are usually set to 1. M_k(t) represents the set of positions that are not detected by ant k in iteration t.

In iteration t + 1, the pheromone of path i⟶j is defined as

()

where τ_ij(t) is the pheromone of path i⟶j in iteration t, ρ is an evaporation coefficient, τ_ij(t) is the pheromone variation of path i⟶j in iteration t, Q is a user-defined constant, and S_k(t) is the path length of ant k in iteration t.

3.3. BNs

A BN is a network structure based on a directed acyclic graph, used to represent dependencies among observed variables. In this network, nodes represent either SNPs or phenotypes, and edges connecting nodes signify causal dependencies. The K2 score, based on BN, is widely used to quantify causal dependencies between two variables.

The K2 score is derived from the Bayesian score. The Bayesian score computes the posterior probability P(M|D) of the BN model M given the data D, which can be written as

()

where P(D|M) is the class-conditional density and P(D) and P(M) are the probabilities of the data D and the model M, respectively. Building upon prior studies [41, 46, 47], in the context of a case-control study, if all variables in the directed acyclic graph are discrete, we can derive

()

where I is the number of combinations of SNP nodes with different genotypes, r_i is the case number of SNP nodes taking the i_th combination numbers, and r_ij is the number of cases with phenotypes taking the j_th state while its parents take the i_th combination. J is the state number of phenotypes. α_ij is the prior belief about case numbers with model nodes taking the i_th combination and j_th state, which is a hyperparameter when the model satisfies the Dirichlet distribution. If α_ij = 1, P(M) and P(D) are constants, then,

()

The Bayesian score can be transformed into the K2 score. Subsequently, the logarithmic form of the K2 score can be derived.

()

3.4. ACOCMPMI

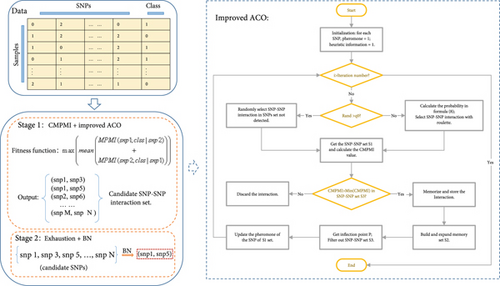
Figure 1 is the flow chart of ACOCMPMI. It can be seen that the ACOCMPMI mainly consists of two parts: Stage 1 (CMPMI + improved ACO) and Stage 2 (exhaustion search + BN). Among them, Stage 1 is the highlight of ACOCMPMI.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Flow chart of the ACOCMPMI.

3.5. CMPMI

The MPMI possesses several properties that prove beneficial for the investigation of epistatic interaction detection. For instance, (1) MPMI(X; Y|Z) ≥ 0; (2) MPMI(X; Y|Z) = 0 if and only if there is no direct association between X and Y under the condition of Z; (3) when both X and Y are independent of Z, MPMI(X; Y|Z) = CMI(X; Y|Z) = MI(X; Y); (4) MPMI(X; Y|Z) is a vsconstant when X is directly associated with Y regardless of the influence intensity of Z on their association; (5) for the target variables X and Y, MPMI(X; Y|Z) = MPMI(Y; X|Z).

It is seen that the MPMI can be regarded as “asymmetric” for the two-order SNP combination (X, Z) and the phenotype Y, which is inconsistent with the basic principle of association. Hence, to capture symmetric information in the detection of two-order epistatic interactions, we define the CMPMI as

()

CMPMI is essentially the mean form of MPMI between the involved target variables, indicating the integration of association information related to SNPs and phenotypes. Furthermore, CMPMI incorporates the interconnectedness of SNP combinations, making it symmetric in terms of describing associations.

3.6. An Improved ACO∗

Given that the basic ACO∗ exhibits low convergence speed and faces challenges with local minima problems [28, 48–50], we developed an improved ACO∗.

To avoid getting trapped in local optima, it is crucial to expand the search space for ants. Based on the original path selection strategy, incorporating suitable random strategies can guide ants out of cyclic paths, thereby providing them with a more diverse set of path selections [51]. The corresponding formulas for path selection can be written as

()

where

is the probability that ant k selects SNP i in iteration t, R is the original path selection strategy, q is a randomly generated value satisfying a uniform distribution, and q₀ is the user specified threshold that is set to the reciprocal of the number of iterations.

For pheromone updating, the original updating strategy is adopted. Thus,

can be written as

()

where

is the pheromone variation of SNP i selected by ant k at iteration t,

represents the set of ants that select SNP i at iteration t, CMPMI(S) represents the CMPMI value of SNP combination S.

The memory-based strategy can retain superior solutions generated in each iteration, enhancing the overall convergence of the algorithm [51, 52]. Specifically, for each iteration, solutions captured by ants are sorted in descending order based on their CMPMI values. Subsequently, a turning point can be determined.

()

where CMPMI(S_g) is the CMPMI value of the SNP combination S_g, g represents the ant. In each iteration, SNP combinations before the turning point are regarded as candidate solutions, and their corresponding fitness values are stored.

To further expedite convergence, a filtering operation based on the memory strategy is incorporated into ACOCMPMI. Within the candidate solution set obtained from each iteration, min(CMPMI) is utilized as the filter criterion. For subsequent iterations, those SNP combinations with CMPMI values greater than the filter criterion are retained and stored in the candidate solution set.

4. Results and Discussion

4.1. Evaluation Metrics

In the experiments, three evaluation metrics, including detection power, F-measure, and running time, are employed to assess the performance of compared methods.

Detection power is a widely used and effective metric for assessing the performance of methods for detecting epistatic interactions [39] and is defined as

()

where D_T is the number of datasets that epistatic interaction models in them are successfully detected and D is the total number of datasets. Besides, the F-measure is defined as

()

where true positives (TPs) represent that the detected SNP combinations are truly associated with the phenotype, false positives (FPs) represent that the detected SNP combinations are not associated with the phenotype, and false negatives (FNs) represent that the undetected SNP combinations are indeed associated with the phenotype.

4.2. Simulation Datasets

There are 11 epistatic interaction models to evaluate the performance of compared methods, where Models 1–8 are models displaying marginal effects (DMEs), and Models 9–11 are models displaying no marginal effects (DNMEs). Table 1 lists details of these models, in which MAF represents minor allele frequency, AA is the homozygous common genotype, Aa is the heterozygous genotype, and aa is the homozygous minor genotype [49, 53]. Using these models, the simulator EpiSIM was applied to generate datasets of different scales [54]. For small-scale datasets, each model was used to generate 100 datasets, in which the sample number is 4000 and the SNP number is 100. For large-scale datasets, each model was used to generate 50 datasets, in which the sample number is 4000 and the SNP number is 1000.

Table 1. Details of epistatic interaction models.

Models	MAF(a)	MAF(b)	*AABB*	*AABb*	*AAbb*	*AaBB*	*AaBb*	*Aabb*	*aaBB*	*aaBb*	*aabb*
Model 1	0.2	0.2	0.087	0.087	0.087	0.087	0.146	0.190	0.087	0.190	0.247
Model 2	0.5	0.5	0.009	0.009	0.009	0.013	0.006	0.006	0.013	0.006	0.006
Model 3	0.5	0.5	0.092	0.092	0.092	0.092	0.319	0.319	0.092	0.319	0.319
Model 4	0.2	0.2	0.084	0.084	0.084	0.084	0.210	0.210	0.084	0.210	0.210
Model 5	0.5	0.5	0.052	0.052	0.052	0.052	0.137	0.137	0.052	0.137	0.137
Model 6	0.5	0.5	0.072	0.164	0.164	0.164	0.072	0.072	0.164	0.072	0.072
Model 7	0.5	0.5	0.067	0.155	0.155	0.155	0.067	0.067	0.155	0.067	0.067
Model 8	0.3	0.3	0.486	0.960	0.538	0.947	0.004	0.811	0.640	0.606	0.909
Model 9	0.2	0.5	0.103	0.063	0.124	0.098	0.086	0.069	0.021	0.147	0.059
Model 10	0.5	0.5	0.000	0.000	0.000	0.000	0.050	0.000	0.100	0.000	0.000
Model 11	0.3	0.3	0.000	0.020	0.000	0.020	0.000	0.020	0.000	0.020	0.000

4.3. Results on Simulation Datasets

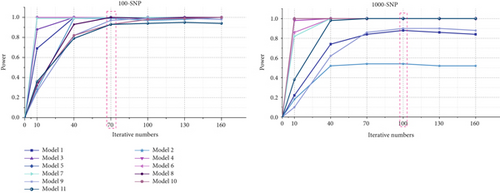
For small-scale datasets, the ant number and the iteration number are set to 200 and 70, respectively, while for large-scale datasets, the ant number and the iteration number are set to 2000 and 100, respectively. The detection power of ACOCMPMI with different iteration numbers is precomputed for all models, and those iteration numbers close to the optimal convergence point are selected as the iteration parameters, as illustrated in Figure 2.

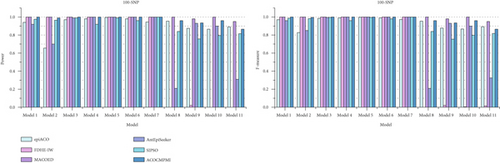
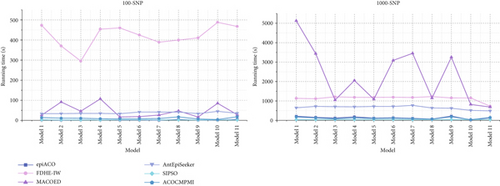
For small-scale datasets, detection power and F-measure of compared methods are presented in Figure 3. In terms of detection power, most methods perform well and detect almost all epistatic interactions in various datasets. Specifically, ACOCMPMI demonstrates high and stable detection power in DMEs, comparable to FDHE-IW and MACOED. Notably, FDHE-IW is a method specifically designed for detecting DMEs [55]. ACOCMPMI exhibits lower detection power than MACOED in small-scale DNME datasets, contrasting with its superior performance in large-scale datasets. Although AntEpiSeeker performs effectively in Model 4–7 datasets, it fails to detect epistatic interactions in Model 2, 8, and 11 datasets, implying that AntEpiSeeker may be inconsistent and exhibit model preference. SIPSO shows similar performance to AntEpiSeeker but with greater stability. However, SIPSO struggles to adapt to DNMEs. In terms of F-measure, ACOCMPMI significantly outperforms most compared methods in DMEs, though its performance is inferior to MACOED in DNMEs.

For large-scale datasets, detection power and F-measure of compared methods are presented in Figure 4. In terms of detection power, ACOCMPMI outperforms all compared methods in almost all datasets except Model 1–2 datasets. Performance of ACOCMPMI ranks second only to SIPSO in Model 1 datasets and to FDHE-IW in Model 2 datasets, respectively, further demonstrating the stability of its detection capability. AntEpiSeeker and MACOED show detection power ranging from 0.1 to 0.5 in most models, which is significantly lower than the detection power of ACOCMPMI. SIPSO performs effectively in datasets of Models 1, 5, and 9–11, but fails to identify over 60% of epistatic interactions in other datasets. epiACO and FDHE-IW exhibit detection power comparable to ACOCMPMI. epiACO performs well in most models since both it and ACOCMPMI use the ACO∗ and the information theory-based quantification measure. In terms of F-measure, ACOCMPMI has higher values than those of compared methods in almost all datasets except Model 1–2 datasets. Although epiACO and FDHE-IW are as effective as ACOCMPMI in identifying epistatic interactions in most models, their F-measure values vary widely among models, implying that both have weaker stability than ACOCMPMI. SIPSO, AntEpiSeeker, and MACOED generally have low F-measure values in most models, which is consistent with their performance in detection power.

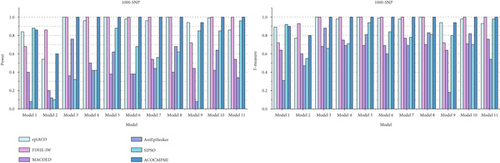
Running times of compared methods in different datasets are shown in Figure 5. It is seen that in small-scale datasets, ACOCMPMI has similar running times to those of both epiACO and SIPSO in various models. Running times of AntEpiSeeker in all models are relatively stable, though it takes more time than ACOCMPMI, epiACO, and SIPSO. MACOED shows significantly varying running times across models, implying that it is sensitive to model type. FDHE-IW requires unacceptable running times in all models. For large-scale datasets, in DMEs and DNMEs, ACOCMPMI has a clear advantage in terms of running time. Unlike FDHE-IW, which has the worst running times in small-scale datasets, MACOED becomes the most time-consuming method in large-scale datasets. Though SIPSO and epiACO have acceptable running times, their detection power is low.

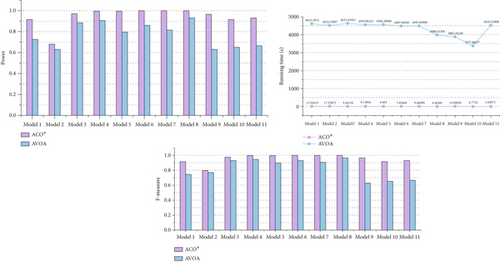
To demonstrate that the improved ACO∗ in ACOCMPMI is effective for searching epistatic interactions, ACO∗ is compared with AVOA in small-scale datasets, using CMPMI as their fitness function, in terms of detection power, F-measure, and running time, as shown in Figure 6. It is seen that even when facing the recently developed meta-heuristic algorithm AVOA, ACO∗ still has an advantage in search performance. In general, the random strategy and memory-filter strategy incorporated into the basic ACO∗ improve its detection capability without increasing running time.

4.4. Case Study

ACOCMPMI is applied to a real AMD dataset to detect two-order epistatic interactions. The AMD dataset contains 103,611 SNPs with 50 controls and 96 cases and has become a widely used benchmark dataset [39, 53]. ACOCMPMI runs four times on this AMD dataset, using ants and iterations as (10,000, 500), (10,000, 1000), (20,000, 250), and (20,000, 1000), respectively, to capture more epistatic interactions. Table 2 lists the Top 15 detected epistatic interactions associated with AMD.

Table 2. Top 15 detected epistatic interactions associated with AMD.

SNP 1			SNP 2			Fitness value	p value	Times
Name	Gene	Chr	Name	Gene	Chr	Fitness value	p value	Times
rs3775652	INPP4B	4	rs380390	CFH	1	123.48	0.0175	3
rs3775652	INPP4B	4	rs725518	RRM1	11	121.99	0.0149	3
rs380390	CFH	1	rs725518	RRM1	11	121.05	0.0039	3
rs380390	CFH	1	rs54816	RRM1	11	120.19	0.0064	3
rs3775652	INPP4B	4	rs54816	RRM1	11	119.90	0.0081	3
rs7863587	/	9	rs380390	CFH	1	119.63	0.0415	2
rs4772270	PCCA	13	rs380390	CFH	1	118.82	0.0265	1
rs6480996	/	10	rs380390	CFH	1	118.11	0.0052	1
rs2019727	CFH	1	rs380390	CFH	1	118.05	0.0082	1
rs380390	CFH	1	rs365299	/	1	117.10	0.0190	1
rs3775652	INPP4B	4	rs4772270	PCCA	13	115.98	0.0458	1
rs7863587	/	9	rs3775652	INPP4B	4	115.49	0.0394	1
rs3775652	INPP4B	4	rs3775650	INPP4B	4	113.31	0.0234	1
rs3775650	INPP4B	4	rs4772270	PCCA	13	112.69	0.0046	1
rs7863587	/	9	rs725518	RRM1	11	111.21	0.0285	1

rs380390 is a G/A/T/C single-nucleotide variation in the CFH gene on human chromosome 1, and rs2019727, also located in CFH, is considered to be significantly associated with AMD in several studies [56–61]. rs3775652 is a C/T single-nucleotide variation located in the INPP4B gene on chromosome 4, and rs725518 is an A/G single-nucleotide variation in the RRM1 gene on chromosome 11, both of which have been detected as AMD-related SNPs [62, 63]. rs4772270 is a G/A/T/C single-nucleotide variation in the PCCA gene on chromosome 13, which has also been reported to be associated with AMD [55, 62, 63]. More recently, rs7863587 was reported to be highly associated with AMD [64]. Although further experiments and clinical studies are needed to confirm real epistatic interactions with AMD, we hope that these findings of ACOCMPMI can provide some clues for the pathological study of AMD.

5. Conclusions and Future Works

Epistatic interaction detection plays a pivotal role in understanding the genetic mechanisms underlying complex diseases. The effectiveness of epistatic interaction detection methods primarily depends on their interaction quantification measures and search strategies. Therefore, both are significant challenges for epistatic interaction detection. In this study, ACOCMPMI, a two-stage ACO∗ based on composite MPMI is proposed for detecting epistatic interactions. In the first stage, CMPMI is introduced to quantify epistatic interactions, and an improved ACO∗, incorporating filter and memory strategies, is employed to search for epistatic interactions. In the second stage, an exhaustive strategy and a BN score, that is, K2 score, are adopted to further identify epistatic interactions within the candidate SNP set obtained from the first stage. ACOCMPMI is compared with five state-of-the-art methods, including epiACO, FDHE-IW, AntEpiSeeker, SIPSO, and MACOED, using simulation data based on 11 epistatic interaction models. Furthermore, ACOCMPMI is applied to detect epistatic interactions in a real dataset related to AMD. The experimental results show that ACOCMPMI is an alternative method for epistatic interaction detection. The time complexity of ACOCMPMI is O(NT + nm²), where N, T, n, and m are numbers of ants, iterations, SNPs, and samples, respectively.

However, there are still several limitations in ACOCMPMI, which inspire us to continue working. First, how to adjust parameter settings to adapt to different scales of input SNP datasets should be further discussed. Second, the practical applicability and scalability of ACOCMPMI require a more detailed analysis. Although some of the identified SNPs have been validated, it remains unclear whether their two-order combinations are indeed causal factors of AMD. Furthermore, the current version of ACOCMPMI focuses on capturing two-order epistatic interactions. In reality, complex diseases are often caused by epistatic interactions with different orders, especially higher orders. Therefore, its future version should be developed to detect higher order epistatic interactions.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Yan Sun and Jing Wang contributed equally to this work.

Funding

This work was supported by the National Natural Science Foundation of China (62472250, 62473179, and 62172254).

Open Research

Data Availability Statement

Data is available on request.

References

1 Dinu I., Mahasirimongkol S., Liu Q., Yanai H., Sharaf Eldin N., Kreiter E., Wu X., Jabbari S., Tokunaga K., and Yasui Y., SNP-SNP Interactions Discovered by Logic Regression Explain Crohn′s Disease Genetics, PLoS One. (2012) 7, no. 10, e43035, https://doi.org/10.1371/journal.pone.0043035, 2-s2.0-84867411475, 23071489.
10.1371/journal.pone.0043035
CAS PubMed Web of Science® Google Scholar
2 Ritchie M. D., Using Biological Knowledge to Uncover the Mystery in the Search for Epistasis in Genome-Wide Association Studies, Annals of Human Genetics. (2011) 75, no. 1, 172–182, https://doi.org/10.1111/j.1469-1809.2010.00630.x, 2-s2.0-78650136869, 21158748.
10.1111/j.1469-1809.2010.00630.x
PubMed Web of Science® Google Scholar
3 Zhao T., Hu Y., Zang T., and Wang Y., Integrate GWAS, eQTL, and mQTL Data to Identify Alzheimer’s Disease-Related Genes, Frontiers in Genetics. (2019) 10, https://doi.org/10.3389/fgene.2019.01021, 31708967.
10.3389/fgene.2019.01021
PubMed Web of Science® Google Scholar
4 Sailer Z. R. and Harms M. J., Detecting High-Order Epistasis in Nonlinear Genotype-Phenotype Maps, Genetics. (2017) 205, no. 3, 1079–1088, https://doi.org/10.1534/genetics.116.195214, 2-s2.0-85020084429, 28100592.
10.1534/genetics.116.195214
CAS PubMed Web of Science® Google Scholar
5 Jiang Y. and Reif J. C., Efficient Algorithms for Calculating Epistatic Genomic Relationship Matrices, Genetics. (2020) 216, no. 3, 651–669, https://doi.org/10.1534/genetics.120.303459, 32973077.
10.1534/genetics.120.303459
PubMed Web of Science® Google Scholar
6 Morrison A. J., Wonderlick D. R., and Harms M. J., Ensemble Epistasis: Thermodynamic Origins of Nonadditivity Between Mutations, Genetics. (2021) 219, no. 1, https://doi.org/10.1093/genetics/iyab105, 34849909.
10.1093/genetics/iyab105
PubMed Web of Science® Google Scholar
7 Wienbrandt L., Kässens J. C., Hübenthal M., and Ellinghaus D., 1000× Faster Than PLINK: Combined FPGA and GPU Accelerators for Logistic Regression-Based Detection of Epistasis, Journal of Computational Science. (2019) 30, 183–193, https://doi.org/10.1016/j.jocs.2018.12.013, 2-s2.0-85059124705.
10.1016/j.jocs.2018.12.013
Google Scholar
8 Wan X., Yang C., Yang Q., Xue H., Fan X., Tang N. L., and Yu W., BOOST: A Fast Approach to Detecting Gene-Gene Interactions in Genome-Wide Case-Control Studies, The American Journal of Human Genetics. (2010) 87, no. 3, 325–340, https://doi.org/10.1016/j.ajhg.2010.07.021, 2-s2.0-77956395423, 20817139.
10.1016/j.ajhg.2010.07.021
CAS PubMed Web of Science® Google Scholar
9 Xie M., Li J., and Jiang T., Detecting Genome-Wide Epistases Based on the Clustering of Relatively Frequent Items, Bioinformatics. (2012) 28, no. 1, 5–12, https://doi.org/10.1093/bioinformatics/btr603, 2-s2.0-84855175318, 22053078.
10.1093/bioinformatics/btr603
CAS PubMed Web of Science® Google Scholar
10 Pitsillou M. and Fokianos K., dCovTS: Distance Covariance/Correlation for Time Series, 2016, The R Foundation for Statistical Computing.
Google Scholar
11 Ding Q., Shang J., Sun Y., Liu G., Li F., Yuan X., and Liu J.-X., NIPMI: A Network Method Based on Interaction Part Mutual Information to Detect Characteristic Genes From Integrated Data on Multi-Cancers, IEEE Access. (2019) 7, 135845–135854, https://doi.org/10.1109/ACCESS.2019.2941520.
10.1109/ACCESS.2019.2941520
Web of Science® Google Scholar
12 Zhang X., Zhao X.-M., He K., Lu L., Cao Y., Liu J., Hao J.-K., Liu Z.-P., and Chen L., Inferring Gene Regulatory Networks From Gene Expression Data by Path Consistency Algorithm Based on Conditional Mutual Information, Bioinformatics. (2012) 28, no. 1, 98–104, https://doi.org/10.1093/bioinformatics/btr626, 2-s2.0-84855160951, 22088843.
10.1093/bioinformatics/btr626
CAS PubMed Web of Science® Google Scholar
13 Kontio J. A., Rinta-Aho M. J., and Sillanpää M. J., Estimating Linear and Nonlinear Gene Coexpression Networks by Semiparametric Neighborhood Selection, Genetics. (2020) 215, no. 3, 597–607, https://doi.org/10.1534/genetics.120.303186, 32414870.
10.1534/genetics.120.303186
CAS PubMed Web of Science® Google Scholar
14 Hernández Lahme D. G. and Samengo I., Estimating the Mutual Information Between Two Discrete, Asymmetric Variables With Limited Samples, Entropy. (2019) 21, no. 6, https://doi.org/10.3390/e21060623, 2-s2.0-85068069184.
10.3390/e21060623
Google Scholar
15 Cao X., Yu G., Liu J., Jia L., and Wang J., Clustermi: Detecting High-Order SNP Interactions Based on Clustering and Mutual Information, International Journal of Molecular Sciences. (2018) 19, no. 8, https://doi.org/10.3390/ijms19082267, 2-s2.0-85052087724, 30072632.
10.3390/ijms19082267
PubMed Web of Science® Google Scholar
16 Zhao J., Zhou Y., Zhang X., and Chen L., Part Mutual Information for Quantifying Direct Associations in Networks, Proceedings of the National Academy of Sciences. (2016) 113, no. 18, 5130–5135, https://doi.org/10.1073/pnas.1522586113, 2-s2.0-84965168859, 27092000.
10.1073/pnas.1522586113
CAS PubMed Web of Science® Google Scholar
17 Reshef D. N., Reshef Y. A., Finucane H. K., Grossman S. R., McVean G., Turnbaugh P. J., Lander E. S., Mitzenmacher M., and Sabeti P. C., Detecting Novel Associations in Large Data Sets, Science. (2011) 334, no. 6062, 1518–1524, https://doi.org/10.1126/science.1205438, 2-s2.0-83755163018, 22174245.
10.1126/science.1205438
CAS PubMed Web of Science® Google Scholar
18 Zhang X., Zhao J., Hao J.-K., Zhao X.-M., and Chen L., Conditional Mutual Inclusive Information Enables Accurate Quantification of Associations in Gene Regulatory Networks, Nucleic Acids Research. (2015) 43, no. 5, e31–e31, https://doi.org/10.1093/nar/gku1315, 2-s2.0-84937548212, 25539927.
10.1093/nar/gku1315
PubMed Web of Science® Google Scholar
19 Shi J., Zhao J., Liu X., Chen L., and Li T., Quantifying Direct Dependencies in Biological Networks by Multiscale Association Analysis, IEEE/ACM Transactions on Computational Biology and Bioinformatics. (2020) 17, no. 2, 449–458, https://doi.org/10.1109/TCBB.2018.2846648, 2-s2.0-85048589297, 29994264.
10.1109/TCBB.2018.2846648
CAS PubMed Web of Science® Google Scholar
20 Shang J., Wang J., Sun Y., Li F., Liu J.-X., and Zhang H., Multiscale Part Mutual Information for Quantifying Nonlinear Direct Associations in Networks, Bioinformatics. (2021) 37, no. 18, 2920–2929, https://doi.org/10.1093/bioinformatics/btab182, 33730153.
10.1093/bioinformatics/btab182
CAS PubMed Web of Science® Google Scholar
21 Upton A., Trelles O., Cornejo-García J. A., and Perkins J. R., Review: High-Performance Computing to Detect Epistasis in Genome Scale Data Sets, Briefings in Bioinformatics. (2016) 17, no. 3, 368–379, https://doi.org/10.1093/bib/bbv058, 2-s2.0-84971619991, 26272945.
10.1093/bib/bbv058
PubMed Web of Science® Google Scholar
22 Zhang Y. and Liu J. S., Bayesian Inference of Epistatic Interactions in Case-Control Studies, Nature Genetics. (2007) 39, no. 9, 1167–1173, 17721534.
10.1038/ng2110
CAS PubMed Web of Science® Google Scholar
23 Abedi M. and Gharehchopogh F. S., An Improved Opposition Based Learning Firefly Algorithm With Dragonfly Algorithm for Solving Continuous Optimization Problems, Intelligent Data Analysis. (2020) 24, no. 2, 309–338, https://doi.org/10.3233/IDA-194485.
10.3233/IDA-194485
Web of Science® Google Scholar
24 Gharehchopogh F. S., Advances in Tree Seed Algorithm: A Comprehensive Survey, Archives of Computational Methods in Engineering. (2022) 29, no. 5, 3281–3304, https://doi.org/10.1007/s11831-021-09698-0.
10.1007/s11831-021-09698-0
Web of Science® Google Scholar
25 Gharehchopogh F. S., An Improved Tunicate Swarm Algorithm With Best-Random Mutation Strategy for Global Optimization Problems, Journal of Bionic Engineering. (2022) 19, no. 4, 1177–1202, https://doi.org/10.1007/s42235-022-00185-1.
10.1007/s42235-022-00185-1
Web of Science® Google Scholar
26 Maciel O., Cuevas E., Navarro M. A., Zaldívar D., and Hinojosa S., Side-Blotched Lizard Algorithm: A Polymorphic Population Approach, Applied Soft Computing. (2020) 88, 106039, https://doi.org/10.1016/j.asoc.2019.106039.
10.1016/j.asoc.2019.106039
Web of Science® Google Scholar
27 Abdollahzadeh B., Gharehchopogh F. S., and Mirjalili S., African Vultures Optimization Algorithm: A New Nature-Inspired Metaheuristic Algorithm for Global Optimization Problems, Computers & Industrial Engineering. (2021) 158, 107408, https://doi.org/10.1016/j.cie.2021.107408.
10.1016/j.cie.2021.107408
Web of Science® Google Scholar
28 Shang J., Wang X., Wu X., Sun Y., Ding Q., Liu J.-X., and Zhang H., A Review of Ant Colony Optimization Based Methods for Detecting Epistatic Interactions, IEEE Access. (2019) 7, 13497–13509, https://doi.org/10.1109/ACCESS.2019.2894676, 2-s2.0-85061743425.
10.1109/ACCESS.2019.2894676
Web of Science® Google Scholar
29 Mohammadzadeh H. and Gharehchopogh F. S., Feature Selection With Binary Symbiotic Organisms Search Algorithm for Email Spam Detection, International Journal of Information Technology & Decision Making. (2021) 20, no. 1, 469–515, https://doi.org/10.1142/S0219622020500546.
10.1142/S0219622020500546
Web of Science® Google Scholar
30 Ghafori S. and Gharehchopogh F. S., Advances in Spotted Hyena Optimizer: A Comprehensive Survey, Archives of Computational Methods in Engineering. (2022) 29, no. 3, 1569–1590, https://doi.org/10.1007/s11831-021-09624-4.
10.1007/s11831-021-09624-4
Web of Science® Google Scholar
31 Zaldívar D., Morales B., Rodríguez A., Valdivia-G A., Cuevas E., and Pérez-Cisneros M., A Novel Bio-Inspired Optimization Model Based on Yellow Saddle Goatfish Behavior, Biosystems. (2018) 174, 1–21, https://doi.org/10.1016/j.biosystems.2018.09.007, 2-s2.0-85054161300, 30261229.
10.1016/j.biosystems.2018.09.007
PubMed Web of Science® Google Scholar
32 Rodríguez A., Camarena O., Cuevas E., Aranguren I., Valdivia-G A., Morales-Castañeda B., Zaldívar D., and Pérez-Cisneros M., Group-Based Synchronous-Asynchronous Grey Wolf Optimizer, Applied Mathematical Modelling. (2021) 93, 226–243, https://doi.org/10.1016/j.apm.2020.12.016.
10.1016/j.apm.2020.12.016
Web of Science® Google Scholar
33 Tuo S., Li C., Liu F., Zhu Y., Chen T., Feng Z., Liu H., and Li A., A Novel Multitasking Ant Colony Optimization Method for Detecting Multiorder SNP Interactions, Interdisciplinary Sciences: Computational LIfe Sciences. (2022) 14, no. 4, 814–832, https://doi.org/10.1007/s12539-022-00530-2, 35788965.
10.1007/s12539-022-00530-2
CAS PubMed Web of Science® Google Scholar
34 Ritchie M. D., Hahn L. W., Roodi N., Bailey L. R., Dupont W. D., Parl F. F., and Moore J. H., Multifactor-Dimensionality Reduction Reveals High-Order Interactions Among Estrogen-Metabolism Genes in Sporadic Breast Cancer, The American Journal of Human Genetics. (2001) 69, no. 1, 138–147, 11404819.
10.1086/321276
CAS PubMed Web of Science® Google Scholar
35 Zheng T., Wang H., and Lo S.-H., Backward Genotype-Trait Association (BGTA)-Based Dissection of Complex Traits in Case-Control Designs, Human Heredity. (2006) 62, no. 4, 196–212, 17114886.
10.1159/000096995
PubMed Web of Science® Google Scholar
36 Lippert C., Listgarten J., Davidson R. I., Baxter J., Poon H., Kadie C. M., and Heckerman D., An Exhaustive Epistatic SNP Association Analysis on Expanded Wellcome Trust Data, Scientific Reports. (2013) 3, no. 1, https://doi.org/10.1038/srep01099, 2-s2.0-84873181536, 23346356.
10.1038/srep01099
PubMed Web of Science® Google Scholar
37 Zhang X., Huang S., Zou F., and Wang W., TEAM: Efficient Two-Locus Epistasis Tests in Human Genome-Wide Association Study, Bioinformatics. (2010) 26, no. 12, i217–i227, https://doi.org/10.1093/bioinformatics/btq186, 2-s2.0-77954182718, 20529910.
10.1093/bioinformatics/btq186
CAS PubMed Web of Science® Google Scholar
38 Tang W., Wu X., Jiang R., and Li Y., Epistatic Module Detection for Case-Control Studies: A Bayesian Model With a Gibbs Sampling Strategy, PLoS Genetics. (2009) 5, no. 5, e1000464, https://doi.org/10.1371/journal.pgen.1000464, 2-s2.0-66649108315, 19412524.
10.1371/journal.pgen.1000464
PubMed Web of Science® Google Scholar
39 Shang J., Sun Y., Liu J.-X., Xia J., Zhang J., and Zheng C.-H., CINOEDV: A Co-Information Based Method for Detecting and Visualizing N-Order Epistatic Interactions, BMC Bioinformatics. (2016) 17, no. 1, 1–15, https://doi.org/10.1186/s12859-016-1076-8, 2-s2.0-84969579622.
10.1186/s12859-016-1076-8
PubMed Web of Science® Google Scholar
40 Wang Y., Liu X., Robbins K., and Rekaya R., AntEpiSeeker: Detecting Epistatic Interactions for Case-Control Studies Using a Two-Stage Ant Colony Optimization Algorithm, BMC Research Notes. (2010) 3, 1–8.
10.1186/1756-0500-3-117
PubMed Google Scholar
41 Jing P.-J. and Shen H.-B., MACOED: A Multi-Objective Ant Colony Optimization Algorithm for SNP Epistasis Detection in Genome-Wide Association Studies, Bioinformatics. (2015) 31, no. 5, 634–641, https://doi.org/10.1093/bioinformatics/btu702, 2-s2.0-84928987535, 25338719.
10.1093/bioinformatics/btu702
CAS PubMed Web of Science® Google Scholar
42 Sun Y., Shang J., Liu J., and Li S., An Improved Ant Colony Optimization Algorithm for the Detection of SNP-SNP Interactions, Intelligent Computing Methodologies: 12th International Conference, ICIC 2016, Lanzhou, China, August 2-5, 2016, Proceedings, Part III 12, 2016, Springer, 21–32.
10.1007/978-3-319-42297-8_3
Google Scholar
43 Tuo S., Li C., Liu F., Li A., He L., Geem Z. W., Shang J., Liu H., Zhu Y., Feng Z., and Chen T. R., MTHSA-DHEI: Multitasking Harmony Search Algorithm for Detecting High-Order SNP Epistatic Interactions, Complex & Intelligent Systems. (2023) 9, no. 1, 637–658, https://doi.org/10.1007/s40747-022-00813-7.
10.1007/s40747-022-00813-7
Web of Science® Google Scholar
44 Tuo S. and Jiang J., A Novel Detection Method for High-Order SNP Epistatic Interactions Based on Explicit-Encoding-Based Multitasking Harmony Search, Interdisciplinary Sciences: Computational LIfe Sciences. (2024) 16, no. 3, 688–711, https://doi.org/10.1007/s12539-024-00621-2.
10.1007/s12539-024-00621-2
PubMed Web of Science® Google Scholar
45 Shang J., Zhang J., Lei X., Zhang Y., and Chen B., Incorporating Heuristic Information Into Ant Colony Optimization for Epistasis Detection, Genes & Genomics. (2012) 34, no. 3, 321–327, https://doi.org/10.1007/s13258-012-0003-2, 2-s2.0-84864146891.
10.1007/s13258-012-0003-2
Web of Science® Google Scholar
46 Bielza C. and Larranaga P., Discrete Bayesian Network Classifiers, ACM Computing Surveys (CSUR). (2014) 47, no. 1, 1–43, https://doi.org/10.1145/2576868, 2-s2.0-84905815981.
10.1145/2576868
Web of Science® Google Scholar
47 Cooper G. F. and Herskovits E., A Bayesian Method for the Induction of Probabilistic Networks From Data, Machine Learning. (1992) 9, no. 4, 309–347, https://doi.org/10.1007/BF00994110.
10.1007/BF00994110
Web of Science® Google Scholar
48 Chowdhury S., Marufuzzaman M., Tunc H., Bian L., and Bullington W., A Modified Ant Colony Optimization Algorithm to Solve a Dynamic Traveling Salesman Problem: A Case Study With Drones for Wildlife Surveillance, Journal of Computational Design and Engineering. (2019) 6, no. 3, 368–386, https://doi.org/10.1016/j.jcde.2018.10.004, 2-s2.0-85063134359.
10.1016/j.jcde.2018.10.004
Web of Science® Google Scholar
49 Dahan F., El Hindi K., Mathkour H., and AlSalman H., Dynamic Flying Ant Colony Optimization (DFACO) for Solving the Traveling Salesman Problem, Sensors. (2019) 19, no. 8, https://doi.org/10.3390/s19081837, 2-s2.0-85065055158, 30999688.
10.3390/s19081837
PubMed Web of Science® Google Scholar
50 Guan B. and Zhao Y., Self-Adjusting Ant Colony Optimization Based on Information Entropy for Detecting Epistatic Interactions, Genes. (2019) 10, no. 2, https://doi.org/10.3390/genes10020114, 2-s2.0-85067260969, 30717303.
10.3390/genes10020114
PubMed Web of Science® Google Scholar
51 Sun Y., Shang J., Liu J.-X., Li S., and Zheng C.-H., epiACO-a Method for Identifying Epistasis Based on Ant Colony Optimization Algorithm, Biodata Mining. (2017) 10, 1–17.
10.1186/s13040-017-0143-7
PubMed Web of Science® Google Scholar
52 Sun Y., Wang X., Shang J., Liu J.-X., Zheng C.-H., and Lei X., Introducing Heuristic Information Into Ant Colony Optimization Algorithm for Identifying Epistasis, IEEE/ACM Transactions on Computational Biology and Bioinformatics. (2020) 17, no. 4, 1253–1261, https://doi.org/10.1109/TCBB.2018.2879673, 2-s2.0-85056174886, 30403637.
10.1109/TCBB.2018.2879673
CAS PubMed Web of Science® Google Scholar
53 Mitchell P., Liew G., Gopinath B., and Wong T. Y., Age-Related Macular Degeneration, Lancet. (2018) 392, no. 10153, 1147–1159, https://doi.org/10.1016/S0140-6736(18)31550-2, 2-s2.0-85053849614.
10.1016/S0140-6736(18)31550-2
PubMed Web of Science® Google Scholar
54 Shang J., Zhang J., Lei X., Zhao W., and Dong Y., EpiSIM: Simulation of Multiple Epistasis, Linkage Disequilibrium Patterns and Haplotype Blocks for Genome-Wide Interaction Analysis, Genes & Genomics. (2013) 35, no. 3, 305–316, https://doi.org/10.1007/s13258-013-0081-9, 2-s2.0-84878761178.
10.1007/s13258-013-0081-9
CAS Web of Science® Google Scholar
55 Tuo S., FDHE-IW: A Fast Approach for Detecting High-Order Epistasis in Genome-Wide Case-Control Studies, Genes. (2018) 9, no. 9, https://doi.org/10.3390/genes9090435, 2-s2.0-85052625255, 30158504.
10.3390/genes9090435
PubMed Web of Science® Google Scholar
56 Lin W.-Y. and Lee W.-C., Incorporating Prior Knowledge to Facilitate Discoveries in a Genome-Wide Association Study on Age-Related Macular Degeneration, BMC Research Notes. (2010) 3, no. 1, 25–26, https://doi.org/10.1186/1756-0500-3-26, 2-s2.0-77949907406.
10.1186/1756-0500-3-26
PubMed Google Scholar
57 Tuo J., Ross R. J., Reed G. F., Yan Q., Wang J. J., Bojanowski C. M., Chew E. Y., Feng X., Olsen T. W., and FerrisF. L.III, The HtrA1 Promoter Polymorphism, Smoking, and Age-Related Macular Degeneration in Multiple Case-Control Samples, Ophthalmology. (2008) 115, no. 11, 1891–1898, https://doi.org/10.1016/j.ophtha.2008.05.021, 2-s2.0-54949101967, 18718667.
10.1016/j.ophtha.2008.05.021
PubMed Web of Science® Google Scholar
58 Tian J., Yu W., Qin X., Fang K., Chen Q., Hou J., Li J., Chen D., Hu Y., and Li X., Association of Genetic Polymorphisms and Age-Related Macular Degeneration in Chinese Population, Investigative Ophthalmology & Visual Science. (2012) 53, no. 7, 4262–4269, https://doi.org/10.1167/iovs.11-8542, 2-s2.0-84866287123, 22618592.
10.1167/iovs.11-8542
CAS PubMed Web of Science® Google Scholar
59 Gili P., Lloreda Martín L., Martín-Rodrigo J.-C., Kim-Yeon N., Modamio-Gardeta L., Fernández-García J. L., Rebolledo-Poves A. B., Gómez-Blazquez E., Pazos-Rodriguez R., Pérez-Fernández E., and Velasco M., Gene Polymorphisms Associated With an Increased Risk of Exudative Age-Related Macular Degeneration in a Spanish Population, European Journal of Ophthalmology. (2022) 32, no. 1, 651–657, https://doi.org/10.1177/11206721211002698, 33765843.
10.1177/11206721211002698
PubMed Web of Science® Google Scholar
60 Feigl B., Morris C. P., Brown B., and Zele A. J., Relationship Among CFH and ARMS2 Genotypes, Macular Pigment Optical Density, and Neuroretinal Function in Persons Without Age-Related Macular Degeneration, Archives of Ophthalmology. (2012) 130, no. 11, 1402–1409, https://doi.org/10.1001/archophthalmol.2012.1940, 2-s2.0-84869123294, 22777494.
10.1001/archophthalmol.2012.1940
PubMed Web of Science® Google Scholar
61 Budzinskaia M., Pogoda T., Generozov É., Chikun E., Shchegoleva I., Kazarian É., and Galoian N., Influence of Genetic Mutations on Clinical Presentation of Subretinal Neovascularization. Report 1: The Impact of CFH and Il-8 Genes Polymorphism, Vestnik Oftalmologii. (2011) 127, no. 4, 3–8, 21882633.
CAS PubMed Google Scholar
62 Tuo S., Zhang J., Yuan X., Zhang Y., and Liu Z., FHSA-SED: Two-Locus Model Detection for Genome-Wide Association Study With Harmony Search Algorithm, PLoS One. (2016) 11, no. 3, e0150669, https://doi.org/10.1371/journal.pone.0150669, 2-s2.0-84962141594, 27014873.
10.1371/journal.pone.0150669
PubMed Web of Science® Google Scholar
63 Guo Y., Zhong Z., Yang C., Hu J., Jiang Y., Liang Z., Gao H., and Liu J., Epi-GTBN: An Approach of Epistasis Mining Based on Genetic Tabu Algorithm and Bayesian Network, BMC Bioinformatics. (2019) 20, no. 1, 1–18, https://doi.org/10.1186/s12859-019-3022-z, 2-s2.0-85071652416.
10.1186/s12859-019-3022-z
PubMed Web of Science® Google Scholar
64 Jiang R., Tang W., Wu X., and Fu W., A Random Forest Approach to the Detection of Epistatic Interactions in Case-Control Studies, BMC Bioinformatics. (2009) 10, no. S1, 1–12, https://doi.org/10.1186/1471-2105-10-S1-S65, 2-s2.0-60849093174.
10.1186/1471-2105-10-S1-S65
PubMed Web of Science® Google Scholar

All articles

ACOCMPMI: An Ant Colony Optimization Algorithm Based on Composite Multiscale Part Mutual Information for Detecting Epistatic Interactions

Abstract

1. Introduction

2. Related Works

3. Materials and Methods

3.1. MPMI

3.2. ACO∗

3.3. BNs

3.4. ACOCMPMI

3.5. CMPMI

3.6. An Improved ACO∗

4. Results and Discussion

4.1. Evaluation Metrics

4.2. Simulation Datasets

4.3. Results on Simulation Datasets

4.4. Case Study

5. Conclusions and Future Works

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley