Recently, the Reconfigurable FSM has drawn the attention of the researchers for multistage signal processing applications. The optimal synthesis of Reconfigurable finite state machine with input multiplexing (Reconfigurable FSMIM) architecture is done by the iterative greedy heuristic based Hungarian algorithm (IGHA). The major problem concerning IGHA is the disintegration of a state encoding technique. This paper proposes the integration of IGHA with the state assignment using logarithmic barrier function based gradient descent approach to reduce the hardware consumption of Reconfigurable FSMIM. Experiments have been performed using MCNC FSM benchmarks which illustrate a significant area and speed improvement over other architectures during field programmable gate array (FPGA) implementation.

1. Introduction

Digital signal processing (DSP) [1–3], pattern matching [4], and circuit testing [5] are the primary applications for most of the digital systems. These applications require a hardware-oriented as well as high-speed control unit. A finite state machine (FSM) is an integral part of any complex digital system. Its inputs are multiplexed to make it hardware oriented, which is known as the finite state machine with input multiplexing (FSMIM). It serves as a control unit, and its operating speed determines the processing speed of the system. The applications as mentioned earlier can be observed as cascaded stages (i.e., multistage) of operations [2], where each stage requires a specific FSM. Hence, a Reconfigurable FSM is investigated in the literature for optimal performance in such applications [6, 7]. A Reconfigurable FSM is defined as a single FSM, which acts as one of the FSMs from the set (i.e., set of FSMs for a specific application) by applying particular mode bits. Its implementation is performed on field programmable gate array (FPGA) platforms [6].

The Reconfigurable FSMIM architecture is created by joining (A) Conventional FSMIM architecture [8] and (B) multiplexer bank (which defines the mode based reconfiguration). The optimal synthesis of both the constituting elements is done by Iterative greedy heuristic based Hungarian algorithm (IGHA) [6]. An efficient state encoding technique for an FSM serves as a vital tool to optimize the hardware utilization while implementing on an FPGA platform [9, 10]. In the case of Reconfigurable FSMIM, the state encoding of the constituent FSMs altogether affects the look-up table (LUT) requirement of the Reconfigurable FSMIM [6].

The major problem concerning IGHA is the disintegration of a state encoding technique. It uses binary state encoding as a default state assignment technique for operation. The state assignment method for the Reconfigurable FSMIM architecture leads to an optimization problem [6]. To the best of the authors’ knowledge, all the state assignment techniques proposed in the literature provide state codes only for a single FSM. Therefore, the objective of this work is the integration of IGHA with an optimal state encoding technique to reduce the hardware consumption of Reconfigurable FSMIM on an FPGA platform.

In the literature, another direction in the implementation of an FSM is RAM-based architectures. The following three types of RAM-based FSM architectures are studied [11]: (a) basic RAM-based FSM architecture, (b) RAM-based FSM architecture with transition-controlled multiplexers, and (c) RAM-based FSM architecture with state-controlled multiplexers. In the basic RAM-based FSM architecture, bits are stored in the form of words. For each transition (i.e., present state combined with the external inputs), the outputs and the state assignment bits for next state are stored in the RAM-word memory [12, 13]. The RAM size required for basic RAM-based FSM implementation is enormous. Hence, to reduce the RAM depth, RAM-based FSM architecture with transition-controlled multiplexers is used. It consists of an input selector bank, which provides active inputs from the external inputs for selecting a particular state [11]. RAM-based FSM architecture with state-controlled multiplexers is used to reduce the RAM size further. It consists of two separate RAM blocks, out of which the smaller RAM block is assigned to operate the input selector bank [11]. Thus, designing such architecture is very complicated.

In this paper, the Improved Reconfigurable FSMIM architecture is proposed, which surmounts the issue of high LUT consumption during FPGA implementation. The proposed architecture is formed using the improved iterative greedy heuristic based Hungarian algorithm (Improved-IGHA). The Improved-IGHA is the integration of IGHA with the state assignment using logarithmic barrier function based gradient descent approach.

To validate the proposed approach, experiments have been performed using MCNC FSM benchmarks [14]. Experimental results for the proposed architecture illustrate a significant area reduction by an average of 20.38% and speed improvement by an average of 32.73% over VRMUX [11] during FPGA implementation. It also demonstrates an adequate area reduction by an average of 16.05% and speed improvement by an average of 1.77% over Reconfigurable FSMIM-S architecture [6] during FPGA implementation. When these results are compared with CRMUX [11], a speed improvement by an average of 11.06% is obtained. The proposed architecture requires an average of 58.38% more LUTs as compared with CRMUX [11] during FPGA implementation. It is the only trade-off for the proposed design.

The remainder of this article is formed as follows. The research problem formulation is made in Section 2. Section 3 consists of state assignment using logarithmic barrier function based gradient descent approach and an illustrative example. Experimental setup and comparative analysis of this work with the literature are devised in Section 4. In the end, concluding remarks are drawn in Section 5.

2. Problem Formulation

Recently, the Reconfigurable FSM has drawn the attention of the researchers for multistage signal processing applications. A novel framework for the creation of Reconfigurable FSMIM is given in [6].

A Mealy FSM is represented in a vector form, such as (S, X, Y, δ, π, S0) where

S = (S0, …, S(M))⟵ set of states;
X = (x₁, …, x_L)⟵ set of input variables;
Y = (y₁, …, y_N)⟵ set of output variables;
δ⇒S∗X → S⟵ transition function;
π⇒S∗X → Y⟵ output function;
S0⟵ initial state.

Moreover, the following variables are defined to illustrate the complete functionality of an FSM:

S(m)⟵ any instantaneous state S(m) ∈ S where m ∈ (0,1, …, M);
K(S(m))⟵ binary state code for the, state S(m) ∈ S;
H = (t₁, …, t_M)⟵ set of number of transitions per state corresponding to S;
h⟵ number of transitions per state where h ∈ (1,2, …, H);
R⟵ the minimum length of a binary-state code, R = ⌈log₂⁡M⌉.

The Reconfigurable FSMIM is defined as a single FSM, which acts as any one of the FSM from the set (i.e., set of FSMs for a specific application) by applying particular mode bits. A set of FSM for a specific application is chosen, where base_ckt⟵ the largest FSM (i.e., the FSM with the highest total number of transitions, states, and inputs) in the set and recon_ckt_1, recon_ckt_2, …, recon_ckt_B⟵ rest of the FSMs in the set. base_ckt-mode is the default mode of operation for the Reconfigurable FSMIM [6].

The Reconfigurable FSMIM architecture is created by joining the following two parts: (A) Conventional FSMIM architecture [8], & (B) Multiplexer bank (which defines the mode based reconfiguration). The optimal synthesis of the Multiplexer bank is done by iterative greedy heuristic based Hungarian algorithm (IGHA) [6]. At the last phase of IGHA, state transitions of each constituent FSM of the Reconfigurable FSMIM architecture are presented in Figure 1. Therefore, the state encoding of the constituent FSMs altogether affects the LUT requirement of the Reconfigurable FSMIM architecture. At the end of IGHA, a modified description of a single FSM (i.e., base_ckt) is obtained which is used to create the Conventional FSMIM part [6].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

State transitions of each constituent FSM of the Reconfigurable FSMIM architecture at the last phase of iterative greedy heuristic based Hungarian algorithm (IGHA).

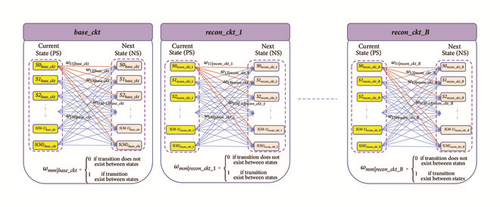
In FSM implementation on an FPGA platform, state encoding technique acts as a tool for minimizing the hardware consumption [9, 10]. For example, an MCNC FSM benchmark tbk requires 82 LUTs when implemented on a Xilinx xc6vlx75t-3 device (Virtex-6) using the Grey encoding technique. But it needs only 41 LUTs on the same platform using the binary encoding technique.

The major problem concerning IGHA is the disintegration of a state encoding technique. It uses binary state encoding as a default state assignment technique for operation [6]. The state assignment method for the Reconfigurable FSMIM architecture leads to an optimization problem as evident from Figure 1. To the best of the authors’ knowledge, all the state assignment techniques proposed in the literature provide state codes only for a single FSM.

Therefore, the objective of this work is the integration of IGHA with an optimal state encoding technique to reduce the hardware consumption of Reconfigurable FSMIM on an FPGA platform.

3. Methodology

This work is an extension of work presented in [6]. Hence, all the variables from [6] are used in the same context throughout the article. An improved version of IGHA (Improved-IGHA) is proposed. It addresses the issue of optimal state encoding.

A recent body of literature has investigated the performance of three fundamental types of state encoding techniques on an FPGA platform [9]. The studied methods are as follows: (a) structural approaches, (b) heuristic approaches, and (c) pragmatic approaches. Out of these three approaches, structural state encoding technique outperforms on an FPGA platform [9, 10]. It uses the knowledge of internal structure (i.e., state transition) of the FSM to generate optimal state codes. Therefore, structural information of FSMs is considered to develop the proposed state encoding technique for the Reconfigurable FSMIM.

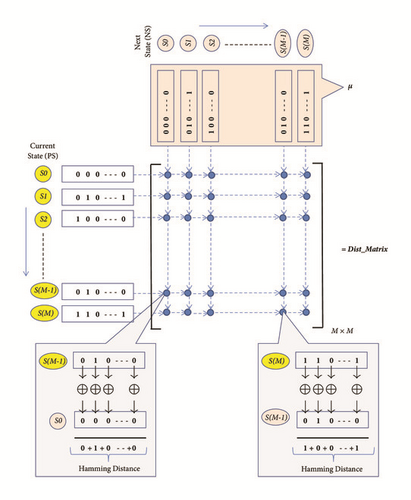
The structural information of the Reconfigurable FSMIM (i.e., state transition) is obtained from Figure 1. Hence, a unified weight matrix is defined by adding the weight of all component FSMs for the same corresponding states. It is given in (1).

The mathematical formulation of the cost function for an FSM is given in [15]. It uses the structural information (i.e., state transitions) of the particular FSM. Let ω_ij⟵ element of weight matrix and Dist_Matrix_ij be the hamming distance between two particular state codes. Dist_Matrix_ij is obtained by counting the number of 1’s after an exclusive-OR operation between the binary state codes as shown in Figure 2. Therefore, from the literature [15], the cost associated with a particular set of state codes (i.e., μ) is defined by (2).

(1)

(2)

3.1. State Assignment Using Logarithmic Barrier Function Based Gradient Descent Approach for the Reconfigurable FSM

Let the graph described by (2) be G_map = (V_map, E_map), where E_map ( i.e., ω_ij) indicates the edge weights between the nodes & V_map ( i.e., columns of μ) represents the set of nodes. Hence, each node corresponds to a particular binary state code because μ_ij opts only the binary labels. M symbolizes the total number of nodes in the graph G_map.

Let a hypercube be characterized as χ_η = (V_χ, E_χ), where η is the dimension, E_χ is the set of edges, and V_χ is the set of vertices of the hypercube [16]. The cardinality of E_χ and V_χ is given in (3) and (4), respectively.

(3)

(4)

Now, the concept of hypercube embedding is used to reduce (2). An embedding is performed from graph G_map onto a hypercube χ_η as described earlier [16, 17]. It is defined as μ : V_map → V_χ which is a one-to-one mapping function. Consequently, M-binary η-vectors are defined as in (5). Thus, if a node of graph G_map (i.e., i) is expressed by a binary state code, the corresponding vertex of the hypercube (i.e., k_i) is represented by the same binary state code.

(5)

In a hypercube, Dist_Matrix_ij (i, j ∈ V_map) represents the hamming distance between k_i and k_j. It is shown in (6), where τ_ij is the instantaneous value of k_ij. The value of τ_ij varies between −1 and 1. Therefore, the cost function is reduced to (7) using hypercube embedding.

(6)

(7)

The objective is thus confined to minimize the cost function given in (7). Evidently, it is a discrete optimization problem, where each state can opt only a particular binary state code.

The convergence of Improved-IGHA depends on the convergence of its constituent algorithms, i.e., IGHA and the applied state assignment technique. Therefore, an algorithm with a high convergence speed is preferred to construct the state assignment technique for Improved-IGHA.

The evolutionary technique, such as genetic algorithm (GA), presents a significant shortcoming as its convergence speed slows down near the global optimum [18, 19]. Similarly, particle swarm optimization (PSO) and differential evolution (DE) operate with a high convergence rate but offer premature convergence which is a critical drawback [20, 21]. In the literature, penalty-based approaches, such as Lagrangian technique and logarithmic-barrier function (LBF) method, have proven their potentials to obtain the optimum solution with a high convergence speed [22, 23]. These methods are advantageous in solving a discrete or combinatorial optimization problem [24, 25].

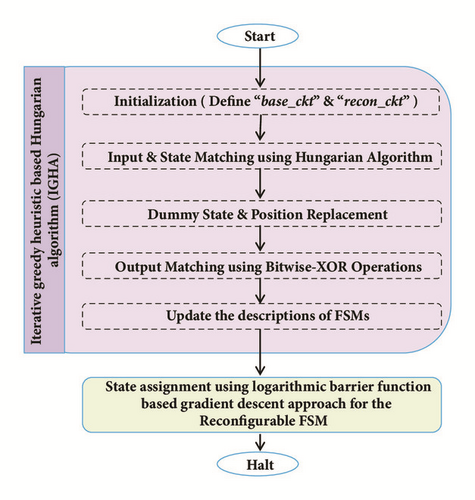
Therefore, the LBF-based Gradient descent approach is adopted to construct the state assignment technique for Improved-IGHA. It is an interior point method that assures the feasible solution. The mathematical formulation of the cost minimization function is performed by LBF. Then, it is reduced iteratively by the gradient-projection approach. The flow chart for the Improved-IGHA is presented in Figure 3.

In LBF technique, the search operation is performed in a continuous space domain to deduce the optimal points. Then, these points are discretized to obtain the optimal solution [26, 27].

In LBF method, an objective function subject to inequality constraints is given in

(8)

The logarithmic barrier function to minimize the cost function (as in (7)) is given in (9). In LBF search, for any move which omits the constraints, the second term serves as a barrier [28] as shown in

(9)

At the iteration iter_t, (9) is defined as shown in

(10)

Initially, LBF selects a feasible τ⁰ and ϕ⁰ > 0. Then, it chooses ϕ^iter_t+1 = σ · ϕ^iter_t, where σ < 1. This iterative process goes on until ϕ^iter_t reaches an adequately small value.

A full-fledged method is required to solve (10) with respect to τ. A first-order gradient-projection approach [29] is well-suited for iteratively minimizing (10). In this approach, the model parameters (a.k.a. weight vectors) are evaluated to minimize the objective function when an analytical calculation is not possible [30, 31]. In this approach, the underlying representation of the objective function of the problem is given in

(11)

An iteration of this projection method is defined by (12). In (12), ρ denotes the step size. ρ is chosen to be a small positive real number [29].

(12)

Thus, small steps (i.e., ρ) are taken in the negative gradient direction of the objective function as illustrated in (12). Then, (13) is used to outline the value of τ on the constraint surface at the next iteration (i.e., τ^(iter_t+1)).

(13)

The convergence criterion for this iterative process is defined by (14), where θ ∈ [0,1].

(14)

In this way, embedding problem is reduced to the determination of M-binary η-vectors (as shown in (15)) which optimizes the cost function (i.e., (7)).

(15)

Hence, the cost function (from (7)) is defined in terms of Hamming distance as shown in

(16)

The constraint (i.e., boundary condition) for this problem is formed, such as any two vertices on hypercube should not contain the same binary state code (i.e., τ_i − τ_j ≠ 0). Hence, the mathematical representation of the constraint is presented in

(17)

By applying (16) and (17) on (9), the objective function for LBF is reduced to

(18)

Therefore, the entity ϑ(τ) (from (13)) is defined by

(19)

The evaluation of the derivative term (i.e., ∇ψ(τ, ϕ)) is required to move in the gradient descent direction as shown in (12). The needed derivative term is obtained by putting (20), (21), (22), and (23) into (18). Hence, ∇ψ(τ, ϕ) is defined by (24).

(20)

(21)

(22)

(23)

(24)

By applying (19) into (13), the normalized vector τ is defined as shown in

(25)

If (14) is satisfied, a solution vector which is defined as

is obtained at the end of the iteration. Therefore, the required set of state codes (i.e.,

) is deduced by discretizing

using

(26)

The pseudocode for the proposed state assignment approach is presented in Algorithm 1.

Algorithm 1: State assignment using logarithmic barrier-function based gradient descent approach for the Reconfigurable FSM.

Input:the objective function defined by Equation (7)
Output:μ^∗ (i.e., the final state code vector)
begin
Initialization: μ ← Binary state codes;
ϕ ← initial_ϕ (s.t. ϕ⁰ > 0);
while (ϕ > final_ϕ)do
repeat
for iter_t ← 1 to θ
τ^iter_t ← τ^(iter_t−1)
−ρ{∇ψ(τ, ϕ)};
/∗by Equation (12)
& Equation (24)∗/
end
return
at the iteration θ);
evaluate
/∗by Equation (26)∗/
Compute cost for the new value of μ
using Equation (7);
if (cost(old_μ)
≥cost(new_μ))then
update, μ^∗ ← new_μ;
else if (cost(old_μ)
<cost(new_μ))then
update, μ^∗ ← old_μ;
end
untilthe algorithm converges
ϕ ← σ · ϕ;
end
returnμ^∗;
end

3.2. An Illustrative Example for the Improved Reconfigurable FSMIM Architecture

The following MCNC FSM benchmarks [14] are considered to demonstrate the steps involved in the creation of the Improved Reconfigurable FSMIM architecture:

(1)
train11 (description is provided in Table 1)
(2)
lion9 (description is provided in Table 2)

Table 1. Description of train11 from MCNC FSM Benchmarks [14].

Input		PS	NS	O/P
x₁	x₂	PS	NS	y₁
0	0	S0	S0	0
1	0	S0	S1	-
0	1	S0	S2	-

1	0	S1	S1	1
0	0	S1	S3	1
1	1	S1	S5	1

0	1	S2	S2	1
0	0	S2	S7	1
1	1	S2	S9	1

0	0	S3	S3	1
0	1	S3	S4	1

0	1	S4	S4	1
0	0	S4	S0	-

1	1	S5	S5	1
0	1	S5	S6	1

0	1	S6	S6	1
0	0	S6	S0	-

0	0	S7	S7	1
1	0	S7	S8	1

1	0	S8	S8	1
0	0	S8	S0	-

1	1	S9	S9	1
1	0	S9	S10	1

1	0	S10	S10	1
0	0	S10	S0	-

Table 2. Description of lion9 from MCNC FSM Benchmarks [14].

Input		PS	NS	O/P
x₁	x₂	PS	NS	y₁
1	0	S0	S1	0
0	0	S0	S0	0

0	0	S1	S0	0
1	0	S1	S1	0
1	1	S1	S2	0

1	0	S2	S1	0
1	1	S2	S2	0
0	1	S2	S3	0

1	1	S3	S2	1
0	1	S3	S3	1
0	0	S3	S4	1

0	1	S4	S3	1
0	0	S4	S4	1
1	0	S4	S5	1

0	0	S5	S4	1
1	0	S5	S5	1
1	1	S5	S6	1

1	0	S6	S5	1
1	1	S6	S6	1
0	1	S6	S7	1

1	1	S7	S6	1
0	1	S7	S7	1
0	0	S7	S8	1

0	1	S8	S7	1
0	0	S8	S8	1

The improved Reconfigurable FSMIM architecture is created by joining (A) Conventional FSMIM architecture and (B) Multiplexer bank (which defines the mode based reconfiguration). The optimal synthesis of the Multiplexer bank is done by the proposed Improved-IGHA. At the end of the proposed algorithm, a modified description of a single FSM (i.e., base_ckt) is obtained which is used to create the Conventional FSMIM part [6]. The Improved-IGHA consists of the following steps:

(i)
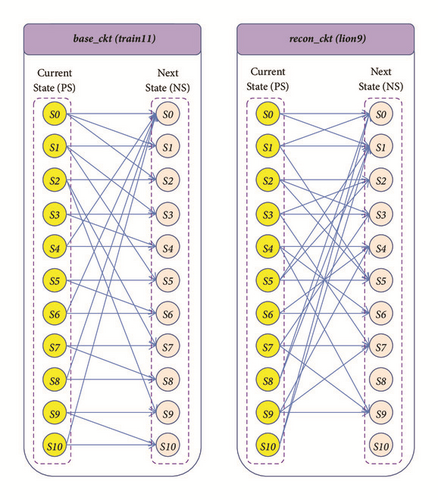
Initialization (Define base_ckt and recon_ckt): train11 is selected as base_ckt because its complexity is greater than lion9 as observed from their descriptions. Consequently, lion9 acts as recon_ckt.
(ii)
Input and State Matching using Hungarian Algorithm: Input and state matchings are performed together using Algorithms 1, 2, 5, and 6 from [6]. Combinations of input lines of base_ckt (i.e., ²P₂ = 2) are generated. For the first combination (x_1∣train11, x_2∣train11), states are matched as S0_lion9 → S0_train11, S1_lion9 → S1_train11, S3_lion9 → S2_train11, S4_lion9 → S3_train11, S7_lion9 → S4_train11, S2_lion9 → S5_train11, S8_lion9 → S6_train11, S5_lion9 → S7_train11, Dummy state → S8_train11, S6_lion9 → S9_train11, and Dummy state → S10_train11. It offers zero assignment_cost and total_cost. For the second combination (x_2∣train11, x_1∣train11), states are matched as S0_lion9 → S0_train11, S3_lion9 → S1_train11, S1_lion9 → S2_train11, S4_lion9 → S3_train11, S5_lion9 → S4_train11, S2_lion9 → S5_train11, Dummy state → S6_train11, S7_lion9 → S7_train11, S8_lion9 → S8_train11, S6_lion9 → S9_train11, and Dummy state → S10_train11. It also offers zero assignment_cost and total_cost. Therefore, the first combination (x_1∣train11, x_2∣train11) is finalized to match with (x_1∣lion9, x_2∣lion9).
(iii)
Dummy State and Position Replacement: The replacements of the dummy states and positions in base_ckt and recon_ckt are performed using Algorithm 3 from [6]. The replaced dummy states (highlighted in “bold italic font”) and dummy positions (highlighted in “bold font”) are presented in Tables 3 and 4.
(iv)
Output Matching using Bitwise-XOR Operations: Output Matching is not required in this case, as there is a single output line in base_ckt as well as in recon_ckt.
(v)
Update the descriptions of FSMs: The updated descriptions of base_ckt and recon_ckt are presented in Tables 3 and 4, respectively.
(vi)
State assignment using logarithmic barrier function based gradient descent approach for the Reconfigurable FSM: The pictorial representation of state transitions for base_ckt and recon_ckt (from Tables 3 and 4) is given in Figure 4. Therefore, the weight matrix ω is formed using (1). It is given in
(27)
The proposed state assignment algorithm starts by considering the binary state codes as an initial solution. It offers the cost as 62 (from (2)).
At the 100^th iteration, the instantaneous value τ (from previous iteration, τ^(iter_99)) is obtained as defined by
(28)
The derivative (from (24)) is evaluated as defined by
(29)
So, the current value of τ (i.e., τ^(iter_100)) is obtained from (12). It is given in (30) by choosing ρ = 10⁻³ (a very small value).
(30)
Then, τ is directed towards the unity radius hypersphere. It is given in
(31)
The required set of state codes is deduced as S0 → 1110, S1 → 1010, S2 → 0000, S3 → 1000, S4 → 0100, S5 → 0010, S6 → 0110, S7 → 1001, S8 → 1101, S9 → 0001, and S10 → 1100 by discretizing the current value of τ using (26). Hence, the cost is reduced to 48 (from (2)).

Table 3. Updated description of train11.

Input		PS	NS	O/P
x₁	x₂	PS	NS	y₁
0	0	S0	S0	0
1	0	S0	S1	-
0	1	S0	S2	-

1	0	S1	S1	1
0	0	S1	S3	1
1	1	S1	S5	1

0	1	S2	S2	1
0	0	S2	S7	1
1	1	S2	S9	1

0	0	S3	S3	1
0	1	S3	S4	1
0	0	S3	S3	1

0	1	S4	S4	1
0	0	S4	S0	-
0	1	S4	S4	1

1	1	S5	S5	1
0	1	S5	S6	1
1	1	S5	S5	1

0	1	S6	S6	1
0	0	S6	S0	-

0	0	S7	S7	1
1	0	S7	S8	1
1	0	S7	S8	1

1	0	S8	S8	1
0	0	S8	S0	-
0	0	S8	S0	-

1	1	S9	S9	1
1	0	S9	S10	1
1	1	S9	S9	1

1	0	S10	S10	1
0	0	S10	S0	-
0	0	S10	S0	-

Table 4. Updated description of lion9.

Input		PS	NS	O/P
x₁	x₂	PS	NS	y₁
0	0	S0	S0	0
1	0	S0	S1	0
0	0	S0	S0	0

1	0	S1	S1	0
0	0	S1	S0	0
1	1	S1	S5	0

0	1	S2	S2	1
0	0	S2	S3	1
1	1	S2	S5	1

0	0	S3	S3	1
0	1	S3	S2	1
1	0	S3	S7	1

0	1	S4	S4	1
0	0	S4	S6	1
1	1	S4	S9	1

1	1	S5	S5	0
0	1	S5	S2	0
1	0	S5	S1	0

0	1	S6	S4	1
0	0	S6	S6	1

0	0	S7	S3	1
1	0	S7	S7	1
1	1	S7	S9	1

1	0	S8	S1	0
0	0	S8	S0	0
0	0	S8	S0	0

1	1	S9	S9	1
1	0	S9	S7	1
0	1	S9	S4	1

1	0	*S10*	S1	0
0	0	*S10*	S0	0
0	0	*S10*	S0	0

In the end, a Bitwise-XOR operation is performed between the updated descriptions of train11 and lion9. It provides the Multiplexer bank (i.e., part-B). The updated descriptions of train11 are used to construct the Conventional FSMIM part (i.e., part-A).

4. Numerical Results and Discussions

To validate the proposed approach, experiments have been performed using MCNC FSM benchmarks [14]. MATLAB (2016b) environment is used to implement the proposed Improved-IGHA. It produces the optimized description for the constituting parts of the Improved Reconfigurable FSMIM architecture. The obtained description is then converted into the Verilog HDL code using MATLAB HDL Coder tool-box. The implementation of the Improved Reconfigurable FSMIM architecture is performed on the Virtex-6 speed-3 device as in [6, 11]. The configuration of the workstation to execute computations is as follows: Intel(R) Core i7 (6th Gen), 16 GB RAM, and 3.5 GHz CPU.

In Improved-IGHA, combinations of input lines, states, and output lines are generated using permutation to perform input, state, and output matching, respectively. The number of input and output lines used for matching is restricted to 7 (i.e., ⁷P₇ = 5040 combinations) to utilize the resources efficiently. Hence, the information content of an input/output line becomes the criteria for selection. An input/output line with high information content is preferred.

The following MCNC FSM benchmarks [14] are selected to illustrate the implementation of the Improved Reconfigurable FSMIM architecture and present its comparative analysis with the existing literature: s1494, s832, s208, planet, s386, sand, mc, styr, cse, ex6, planet1, and s1488.

s1494 is chosen as base_ckt (i.e., the circuit added at the 0^th iteration of Improved-IGHA), as it is more complex (i.e., the total number of transitions is high) as compared with the other FSMs in the set. The other FSMs in the set are added iteratively in the design in their respective order.

In an FSM, a specific state is chosen only if a particular set of input bits (i.e., 1’s or 0’s) are present. Hence, the percentage of 1’s and 0’s together in an input line acts as information content as shown in Table 5 (the selected input lines to match with base_ckt are highlighted). Similarly, the output is always defined by “1.” Hence, the percentage of 1’s in an output line serves as information content as shown in Tables 6 and 7 (the selected output lines to match with base_ckt are highlighted).

Table 5. The information content for input lines of MCNC FSM Benchmarks and their matching with input lines of base_ckt.

FSM	No. of I/P	Input lines with their	Matched with base_ckt	No. of state
FSM	No. of I/P	information content	Matched with base_ckt	No. of state
s1494	8	x₁(99.6%), x₂(10%),	x₁, x₃,	48
		x₃(25.6%), x₄(24.8%),	x₄, x₅,
		x₅(12.4%), x₆(66%),	x₆, x₇,
		x₇(41.6%), x₈(20.4%)	x₈

s832	18	x₁(2.04%), x₂(6.93%),		25
		x₃(2.44%), x₄(4.48%),
		x₅(70.61%), x₆(1.63%),
		x₇(14.28%), x₈(9.79%),	x₉, x₁₁,
		x₉(8.97%), x₁₀(8.16%),	x₁₈, x₁₇,
		x₁₁(8.57%), x₁₂(6.12%),	x₈, x₇, x₅
		x₁₃(4.081%), x₁₄(4.08%),
		x₁₅(1.63%), x₁₆(1.63%),
		x₁₇(59.18%), x₁₈(81.63%),

s208	11	x₁(96.73%), x₂(91.5%),		18
		x₃(0%), x₄(0%),	x₁, x₈,
		x₅(0%), x₆(2.61%),	x₆, x₉,
		x₇(2.61%), x₈(5.22%),	x₁₁, x₂,
		x₉(12.41%), x₁₀(49.01%),	x₁₀
		x₁₁(77.12%)

planet	7	x₁, x₂,	x₆, x₃,	48
		x₃, x₄,	x₄, x₂,
		x₅, x₆,	x₅, x₇,
		x₇	x₁

s386	7	x₁, x₂,	x₄, x₃,	13
		x₃, x₄,	x₂, x₇,
		x₅, x₆,	x₁, x₅,
		x₇	x₆

sand	11	x₁(52.17%), x₂(52.17%),		32
		x₃(52.17%), x₄(52.17%),	x₄, x₂,
		x₅(24.45%), x₆(3.26%),	x₁, x₁₀,
		x₇(18.47%), x₈(26.63%),	x₅, x₃,
		x₉(1.08%), x₁₀(79.89%),	x₈
		x₁₁(19.56%)

mc	3		−, x₃,	4
		x₁, x₂,	x₁,−,
		x₃	x₂, −,
			−

styr	9	x₁(92.16%), x₂(4.81%),		30
		x₃(48.79%), x₄(69.87%),	x₂, x₄,
		x₅(68.67%), x₆(39.15%),	x₅, x₃,
		x₇(4.81%), x₈(5.42%),	x₈, x₆, x₁
		x₉(3.61%)

cse	7	x₁, x₂,	x₅, x₂,	16
		x₃, x₄,	x₇, x₃,
		x₅, x₆,	x₄, x₁,
		x₇	x₆

ex6	5		x₃, x₄,	8
		x₁, x₂,	−, x₁,
		x₃, x₄, x₅	x₂, −,
			x₅

planet1	7	x₁, x₂,	x₅, x₁,	48
		x₃, x₄,	x₆, x₃,
		x₅, x₆,	x₄, x₂,
		x₇	x₇

s1488	8	x₁(98.8%), x₂(12.74%),	x₁, x₅,	48
		x₃(23.5%), x₄(23.9%),	x₃, x₄,
		x₅(16.33%), x₆(65.73%),	x₈, x₇,
		x₇(40.23%), x₈(18.32%)	x₆

Table 6. The information content for output lines of MCNC FSM Benchmarks & their matching with output lines of base_ckt.

FSM	No. of O/P	Output lines with their	Matched with base_ckt
FSM	No. of O/P	information content	Matched with base_ckt
s1494	19	y₁(24.8%), y₂(4.8%), y₃(5.2%),
		y₄(3.2%), y₅(2.4%), y₆(2.4%),	y₁₁, y₁₂,
		y₇(15.2%), y₈(25.2%), y₉(1.6%),	y₁₃, y₁₄,
		y₁₀(6.4%), y₁₁(87.2%), y₁₂(40.4%),	y₁₅, y₁₇,
		y₁₃(32.8%), y₁₄(70.4%), y₁₅(38.4%),	y₁₉
		y₁₆(18.4%), y₁₇(70%), y₁₈(31.2%),
		y₁₉(49.2%)

s832	19	y₁(5.71%), y₂(2.44%), y₃(1.22%),
		y₄(1.63%), y₅(2.44%), y₆(0.81%),	y₁₉, y₁₅,
		y₇(2.44%), y₈(73.06%), y₉(0.81%),	y₂, y₈,
		y₁₀(0.81%), y₁₁(5.3%), y₁₂(2.44%),	y₇, y₁,
		y₁₃(0.81%), y₁₄(1.63%), y₁₅(6.12%),	y₁₁
		y₁₆(0.81%), y₁₇(1.63%), y₁₈(2.44%),
		y₁₉(41.22%)

s208	2	y₁, y₂	−, y₁,
			−, −,
			y₂, −,
			−

planet	19	y₁(54.78%), y₂(23.47%), y₃(69.56%),
		y₄(16.52%), y₅(32.17%), y₆(73.91%),	y₆, y₈,
		y₇(26.08%), y₈(28.69%), y₉(91.3%),	y₉, y₅,
		y₁₀(4.34%), y₁₁(1.73%), y₁₂(22.6%),	y₃, y₁,
		y₁₃(11.3%), y₁₄(2.6%), y₁₅(3.47%),	y₇
		y₁₆(1.73%), y₁₇(3.47%), y₁₈(3.47%),
		y₁₉(20%)

s386	7		y₆, y₁,
		y₁, y₂, y₃,	y₃, y₄,
		y₄, y₅, y₆, y₇	y₇, y₅,
			y₂

sand	9	y₁(22.28%), y₂(36.41%), y₃(16.84%),	y₄, y₆,
		y₄(62.5%), y₅(15.76%), y₆(8.15%),	y₂, y₇,
		y₇(17.39%), y₈(1.63%), y₉(3.26%)	y₃, y₅, y₁

mc	5		y₄, y₂,
		y₁, y₂, y₃,	y₅, y₁,
		y₄, y₅	y₃, −,
			−

styr	10	y₁(15.66%), y₂(33.73%), y₃(25.9%),	y₅, y₆,
		y₄(3.012%), y₅(8.43%), y₆(7.22%),	y₇, y₈,
		y₇(5.42%), y₈(11.445%), y₉(3.614%),	y₃, y₂,
		y₁₀(4.819%)	y₁

cse	7		y₇, y₃,
		y₁, y₂, y₃,	y₅, y₁,
		y₄, y₅, y₆, y₇	y₄, y₆,
			y₂

ex6	8	y₁(58.82%), y₂(29.41%), y₃(55.88%),	y₅, y₈,
		y₄(29.41%), y₅(50%), y₆(26.47%),	y₄, y₁,
		y₇(5.88%), y₈(23.52%)	y₆, y₂, y₃

Table 7. The information content for output lines of MCNC FSM Benchmarks and their matching with output lines of base_ckt.

FSM	No. of O/P	Output lines with their	Matched with base_ckt
FSM	No. of O/P	information content	Matched with base_ckt
planet1	19	y₁(54.78%), y₂(23.47%), y₃(69.56%),
		y₄(16.52%), y₅(32.17%), y₆(73.91%),	y₆, y₇,
		y₇(26.08%), y₈(28.69%), y₉(91.3%),	y₁, y₈,
		y₁₀(4.34%), y₁₁(1.73%), y₁₂(22.6%),	y₅, y₃,
		y₁₃(11.3%), y₁₄(2.6%), y₁₅(3.47%),	y₉
		y₁₆(1.73%), y₁₇(3.47%), y₁₈(3.47%),
		y₁₉(20%)

s1488	19	y₁(2.39%), y₂(2.78%), y₃(1.59%),
		y₄(5.17%), y₅(2.39%), y₆(15.13%),	y₁₈, y₇,
		y₇(71.31%), y₈(3.98%), y₉(51.39%),	y₁₃, y₁₉,
		y₁₀(6.3%), y₁₁(16.7%), y₁₂(37.1%),	y₉, y₁₅,
		y₁₃(70.5%), y₁₄(24.3%), y₁₅(87.6%),	y₁₂
		y₁₆(31.1%), y₁₇(25.4%), y₁₈(31.4%),
		y₁₉(39.84%)

At the first phase of Improved-IGHA, input and state matching are performed together, and optimal assignments (with respect to base_ckt) are made. It is presented in Table 5. All the recon_ckt states are mapped onto base_ckt states in their respective order. Output matching (with respect to base_ckt) is performed iteratively by Bitwise-XOR operations. It is presented in Tables 6 and 7. Then, after updating the descriptions of constituting FSMs, the state assignment using logarithmic barrier function based gradient descent approach is performed.

To present a comparative analysis of the total computation time required by IGHA [6] and Improved-IGHA, an inbuilt feature in MATLAB named “stopwatch timer” is used. It evaluates the elapsed time (i.e., the execution time between the starting and stopping of a function). As evident from the literature [6], linear assignment problems (LAPs) are solved several times by IGHA to perform matchings among all generated combinations to add recon_ckt_b ∈ {recon_ckt_1, …, recon_ckt_B} iteratively. The convergence period of IGHA to solve a single LAP ranges from 0.03 ms to 0.6 ms. Hence, the total elapsed time taken by IGHA (i.e., t_IG) is given in (32). The convergence time for the state assignment using LBF-based gradient descent approach (i.e., t_SE) to add recon_ckt_b ∈ {recon_ckt_1, …, recon_ckt_B} iteratively is given in Table 8. Therefore, the total elapsed time taken by Improved-IGHA (i.e., t_Proposed) is an addition of t_IG and t_SE (from Figure 3). It is presented in Table 8.

(32)

Table 8. Comparative analysis of the total computation time required by IGHA [6] and Improved-IGHA.

Iteration No.	FSM included	Total elapsed time	Total elapsed time	Total elapsed time for Improved-IGHA
	in the specific	for IGHA [6]	for state encoding	(Hrs) t_Proposed = t_IG + t_SE
	iteration	(Hrs) t_IG	tech. (ms) t_SE	∵t_IG ≫ t_SE, ∴t_Proposed≅t_IG
0^th	s1494	0	296.529	0
1^st	s832	25.34	214.468	25.34
2^nd	s208	18.57	156.062	18.57
3^rd	planet	48.65	338.560	48.65
4^th	s386	13.17	182.808	13.17
5^th	sand	32.43	293.894	32.43
6^th	mc	0.182	148.784	0.182
7^th	styr	30.409	249.509	30.409
8^th	cse	16.21	387.923	16.21
9^th	ex6	4.38	167.144	4.38
10^th	planet1	48.544	312.809	48.544
11^th	s1488	48.654	326.406	48.654

The experimental results presented in Table 8 illustrate that the total computation time required by IGHA is far higher than the convergence time for the proposed state assignment technique (i.e., t_IG ≫ t_SE). Therefore, the total computation time required by Improved-IGHA is equivalent to the total computation time needed by IGHA (i.e., t_Proposed≅t_IG).

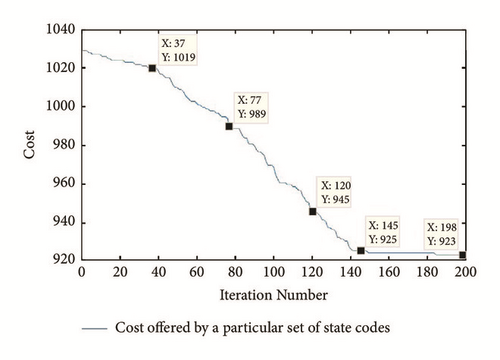
Convergence plot for the state assignment using logarithmic barrier function based gradient descent approach after adding the last constituting FSM in the proposed architecture is presented in Figure 5. It starts by taking binary state codes as an initial code. The cost offered to the proposed architecture is calculated by (2). It converges to 200 iterations. The cost is reduced from 1028 to 923 as shown in Figure 5. Consequently, at 200^th iteration, the following state codes are obtained: S0 → 010111, S1 → 000000, S2 → 000111, S3 → 110000, S4 → 010100, S5 → 110101, S6 → 000110, S7 → 011101, S8 → 001100, S9 → 011010, S10 → 011110, S11 → 001110, S12 → 010110, S13 → 111011, S14 → 000011, S15 → 100110, S16 → 110111, S17 → 001010, S18 → 011100, S19 → 100001, S20 → 101001, S21 → 110010, S22 → 100000, S23 → 001000, S24 → 001111, S25 → 101101, S26 → 010011, S27 → 101010, S28 → 110001, S29 → 001011, S30 → 111010, S31 → 011111, S32 → 000101, S33 → 000100, S34 → 111101, S35 → 000001, S36 → 001101, S37 → 101000, S38 → 000010, S39 → 100111, S40 → 110110, S41 → 011001, S42 → 100010, S43 → 001001, S44 → 010001, S45 → 100101, S46 → 101111, and S47 → 010010.

At the last phase of Improved-IGHA, a mutual Bitwise-XOR operation is conducted between the updated descriptions of FSMs. Therefore, the constituting parts of the proposed architecture are created. The individual share of constituent FSMs in the Improved-Reconfigurable FSMIM architecture is determined by the difference between the occupied LUTs in the recent and its previous iteration. After adding all the constituting FSMs in the proposed design (i.e., at the last iteration), the total LUT consumption and operating frequency are obtained. It is presented in Table 9.

Table 9. Implementation of the Improved Reconfigurable FSMIM architecture on the Virtex-6 speed-3 device in an iterative manner.

Iteration No.	FSM included	#LUTs occupied	Maximum	Maximum	#LUTs occupied by the FSM
	in the specific	in the specific	Operating	Path	(#LUTs in the current iteration
	iteration	iteration	Frequency (MHz)	Delay (ns)	- #LUTs in the previous iteration)
0^th	s1494	40	831.693	3.898	40
1^st	s832	97	803.44	4.288	57
2^nd	s208	114	793.583	5.252	17
3^rd	planet	142	785.326	4.219	28
4^th	s386	157	776.863	4.534	15
5^th	sand	187	760.88	4.117	30
6^th	mc	198	757.237	3.854	11
7^th	styr	217	743.431	4.204	19
8^th	cse	240	713.929	4.401	23
9^th	ex6	249	704.892	4.649	9
10^th	planet1	274	690.83	4.977	25
11^th	s1488	293	676.928	5.151	19

#LUTs → number of LUTs occupied in ISE

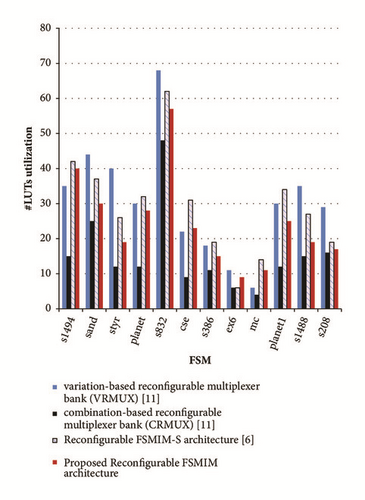
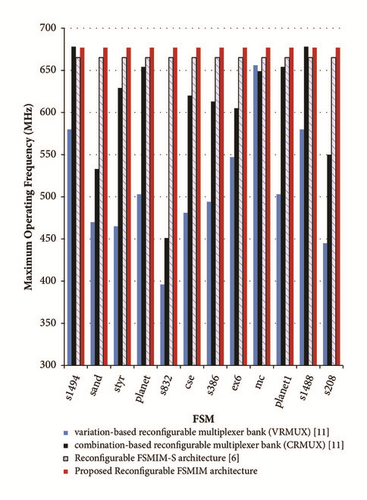
Experimental results for the proposed architecture illustrates a significant area reduction by an average of 20.38% and speed improvement by an average of 32.73% over VRMUX [11] during FPGA implementation. It also demonstrates an adequate area reduction by an average of 16.05% and speed improvement by an average of 1.77% over Reconfigurable FSMIM-S architecture [6] during FPGA implementation. When these results are compared with CRMUX [11], a speed improvement by an average of 11.06% is obtained. The proposed architecture requires an average of 58.38% more LUTs as compared with CRMUX [11] during FPGA implementation. It is the only trade-off for the proposed design. A comparative analysis of the hardware consumption and maximum operating frequency variation on FPGA implementation is presented in Figures 6 and 7, respectively.

5. Concluding Remarks

This article furnishes the framework for the Improved-Reconfigurable FSMIM architecture. The Improved-Reconfigurable FSMIM architecture is created by joining the following two parts: (A) Conventional FSMIM architecture and (B) Multiplexer bank (which defines the mode based reconfiguration). An improved version of iterative greedy heuristic based Hungarian algorithm (Improved-IGHA) is proposed to establish the constituting parts as mentioned earlier. Improved-IGHA is an integration of IGHA [6] and a state assignment using logarithmic barrier function based gradient descent approach. It reduces the hardware consumption of the proposed architecture by performing an optimal state encoding. An illustrative example using MCNC FSM benchmarks is also given to demonstrate the steps involved in the creation of the proposed architecture.

The proposed architecture illustrates a significant area reduction by an average of 20.38% and speed improvement by an average of 32.73% over VRMUX [11] during FPGA implementation. It also demonstrates an adequate area reduction by an average of 16.05% and speed improvement by an average of 1.77% over Reconfigurable FSMIM-S architecture [6] during FPGA implementation. When these results are compared with CRMUX [11], a speed improvement by an average of 11.06% is obtained. The proposed architecture requires an average of 58.38% more LUTs as compared with CRMUX [11] during FPGA implementation. It is the only trade-off for the proposed design.

Further, the proposed architecture will be investigated to develop an efficient architecture for multistage signal processing [1, 2] and circuit testing [5] based applications.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

The datasets generated during and/or analyzed during the current study are available in [6] repository [DOI: 10.1155/2018/6831901]. This work is conducted in the Department of ECE, SRM Institute of Science and Technology, Kattankulathur-603203, Chennai, India.

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 De Lucas E., Sanchez-Elez M., and Pardines I., DSPONE48: a methodology for automatically synthesize HDL focus on the reuse of DSP slices, Journal of Parallel and Distributed Computing. (2017) 106, 132–142, https://doi.org/10.1016/j.jpdc.2017.01.021, 2-s2.0-85011999976.
10.1016/j.jpdc.2017.01.021
Web of Science® Google Scholar
2 Wu J., Yang D., and Chen Z., Design and application of multi-stage reconfigurable signal processing flow on FPGA, Computers and Electrical Engineering. (2015) 42, 1–11, 2-s2.0-84961289358, https://doi.org/10.1016/j.compeleceng.2014.12.001.
10.1016/j.compeleceng.2014.12.001
Web of Science® Google Scholar
3 Zheng J., Gao W., Wu D., and Xie D., An efficient VLSI architecture for CBAC of AVS HDTV decoder, Signal Processing: Image Communication. (2009) 24, no. 4, 324–332, 2-s2.0-67349091422, https://doi.org/10.1016/j.image.2008.12.007.
10.1016/j.image.2008.12.007
Web of Science® Google Scholar
4 Rafla N. I. and Gauba I., A reconfigurable pattern matching hardware implementation using on-chip RAM-based FSM, Proceedings of the 53rd IEEE International Midwest Symposium on Circuits and Systems, MWSCAS 2010, August 2010, Seattle, Wash, USA, IEEE, 49–52, 2-s2.0-77956602404.
Google Scholar
5 Ling Z., Ji-Shun K., and Zhi-Qiang Y., Virtual scan chains reordering using a RAM-based module for high test compression, Microelectronics Journal. (2012) 43, no. 11, 869–872, 2-s2.0-84866739944, https://doi.org/10.1016/j.mejo.2012.06.003.
10.1016/j.mejo.2012.06.003
Web of Science® Google Scholar
6 Das N. and Priya P. A., FPGA implementation of reconfigurable finite state machine with input multiplexing architecture using hungarian method, International Journal of Reconfigurable Computing. (2018) 2018, 15, 6831901, 2-s2.0-85042641929.
10.1155/2018/6831901
Google Scholar
7 Glaser J., Damm M., Haase J., and Grimm C., TR-FSM: transition-based reconfigurable finite state machine, ACM Transactions on Reconfigurable Technology and Systems (TRETS). (2011) 4, no. 3, article no. 23, 1–14, https://doi.org/10.1145/2000832.2000835, 2-s2.0-84867499389.
10.1145/2000832.2000835
Web of Science® Google Scholar
8 Garcia-Vargas I. and Senhadji-Navarro R., Finite state machines with input multiplexing: a performance study, IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. (2015) 34, no. 5, 867–871, https://doi.org/10.1109/TCAD.2015.2406859, 2-s2.0-84928412902.
10.1109/TCAD.2015.2406859
Web of Science® Google Scholar
9 Jozwiak L., Slusarczyk A., and Gawlowski D., Multi-objective optimal FSM state assignment, Proceedings of the 9th EUROMICRO Conference on Digital System Design (DSD′06), 2006, Dubrovnik, Croatia, IEEE, 385–396, https://doi.org/10.1109/DSD.2006.69.
10.1109/DSD.2006.69
Google Scholar
10 Deniziak S. and Wiśniewski M., FPGA-based state encoding using symbolic functional decomposition, IEEE Electronics Letters. (2010) 46, no. 19, 1316–1318, 2-s2.0-77956825553, https://doi.org/10.1049/el.2010.2002.
10.1049/el.2010.2002
Web of Science® Google Scholar
11 Senhadji-Navaro R. and Garcia-Vargas I., high-speed and area-efficient reconfigurable multiplexer bank for RAM-based finite state machine implementations, Journal of Circuits, Systems and Computers. (2015) 24, no. 7, 1–15, 1550101, https://doi.org/10.1142/S0218126615501017, 2-s2.0-84931568805.
10.1142/S0218126615501017
Web of Science® Google Scholar
12 Kołopieńczyk M., Titarenko L., and Barkalov A., Design of EMB-based moore FSMs, Journal of Circuits, Systems and Computers. (2017) 26, no. 7, 1–23, https://doi.org/10.1142/S0218126617501250.
10.1142/S0218126617501250
Web of Science® Google Scholar
13 Kolopienczyk M., Barkalov A., and Titarenko L., Hardware reduction for RAM-based moore FSMs, Proceedings of the 7th International Conference on Human System Interactions, HSI 2014, June 2014, Costa da Caparica, Portugal, IEEE, 255–260, 2-s2.0-84905678960.
Google Scholar
14 https://people.engr.ncsu.edu/brglez/CBL/benchmark/.
Google Scholar
15 Devadas S., Ma H.-K., Newton A. R., and Sangiovanni-Vincentelli A., Mustang: state assignment of finite state machines targeting multilevel logic implementations, IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. (1988) 7, no. 12, 1290–1300, https://doi.org/10.1109/43.16807, 2-s2.0-0024168714.
10.1109/43.16807
Web of Science® Google Scholar
16 Kabyl K., Berrachedi A., and Sopena É., A note on the cubical dimension of new classes of binary trees, Czechoslovak Mathematical Journal. (2015) 65, no. 1, 151–160, https://doi.org/10.1007/s10587-015-0165-6, MR3336030.
10.1007/s10587-015-0165-6
Web of Science® Google Scholar
17 Liu M. and Liu H.-M., Vertex-fault-tolerant cycles embedding on enhanced hypercube networks, Acta Mathematicae Applicatae Sinica. (2016) 32, no. 1, 187–198, https://doi.org/10.1007/s10255-016-0547-z, MR3482432.
10.1007/s10255-016-0547-z
CAS Google Scholar
18 Pavai G. and Geetha T. V., New crossover operators using dominance and co-dominance principles for faster convergence of genetic algorithms, Soft Computing. (2018) 1–26, 2-s2.0-85040719030.
Web of Science® Google Scholar
19 Ganjefar S. and Tofighi M., Optimization of quantum-inspired neural network using memetic algorithm for function approximation and chaotic time series prediction, Neurocomputing. (2018) 291, 175–186, https://doi.org/10.1016/j.neucom.2018.02.074.
10.1016/j.neucom.2018.02.074
Web of Science® Google Scholar
20 Huang H., Lv L., Ye S., and Hao Z., Particle swarm optimization with convergence speed controller for large-scale numerical optimization, Soft Computing. (2018) 1–17, https://doi.org/10.1007/s00500-018-3098-9.
10.1007/s00500-018-3098-9
Web of Science® Google Scholar
21 Knobloch R., Mlýnek J., and Srb R., The classic differential evolution algorithm and its convergence properties, Applications of Mathematics. (2017) 62, no. 2, 197–208, https://doi.org/10.21136/AM.2017.0274-16, MR3647040.
10.21136/AM.2017.0274-16
Web of Science® Google Scholar
22 Curtis F. E., A penalty-interior-point algorithm for nonlinear constrained optimization, Mathematical Programming Computation. (2012) 4, no. 2, 181–209, https://doi.org/10.1007/s12532-012-0041-4, MR2934972, 2-s2.0-84867137349.
10.1007/s12532-012-0041-4
Google Scholar
23 Armand P. and Omheni R., A mixed logarithmic barrier-augmented Lagrangian method for nonlinear optimization, Journal of Optimization Theory and Applications. (2017) 173, no. 2, 523–547, https://doi.org/10.1007/s10957-017-1071-x, MR3634802, Zbl1370.49022, 2-s2.0-85011304692.
10.1007/s10957-017-1071-x
Web of Science® Google Scholar
24 Murray W. and Ng K.-M., An algorithm for nonlinear optimization problems with binary variables, Computational Optimization and Applications. (2010) 47, no. 2, 257–288, https://doi.org/10.1007/s10589-008-9218-1, MR2718180.
10.1007/s10589-008-9218-1
Web of Science® Google Scholar
25 Soler E. M., De Sousa V. A., and Da Costa G. R. M., A modified primal-dual logarithmic-barrier method for solving the optimal power flow problem with discrete and continuous control variables, European Journal of Operational Research. (2012) 222, no. 3, 616–622, https://doi.org/10.1016/j.ejor.2012.05.021, 2-s2.0-84863990079.
10.1016/j.ejor.2012.05.021
Web of Science® Google Scholar
26 Gárciga Otero R. and Iusem A., A proximal method with logarithmic barrier for nonlinear complementarity problems, Journal of Global Optimization. (2016) 64, no. 4, 663–678, https://doi.org/10.1007/s10898-015-0266-7, MR3475758.
10.1007/s10898-015-0266-7
Web of Science® Google Scholar
27 Menniche L. and Benterki D., A logarithmic barrier approach for linear programming, Journal of Computational and Applied Mathematics. (2016) 312, 267–275, https://doi.org/10.1016/j.cam.2016.05.025, MR3557880.
10.1016/j.cam.2016.05.025
Web of Science® Google Scholar
28 Shen R., Meng Z., Dang C., and Jiang M., Algorithm of barrier objective penalty function, Numerical Functional Analysis and Optimization. (2017) 38, no. 11, 1–17, https://doi.org/10.1080/01630563.2017.1338732, MR3716035.
10.1080/01630563.2017.1338732
Web of Science® Google Scholar
29 Chakroun I., Haber T., and Ashby T. J., SW-SGD: the sliding window stochastic gradient descent algorithm, Procedia Computer Science. (2017) 108, 2318–2322, 2-s2.0-85027379240.
10.1016/j.procs.2017.05.082
Google Scholar
30 Senov A. and Granichin O., Projective approximation based gradient descent modification, IFAC-PapersOnLine. (2017) 50, no. 1, 3899–3904, https://doi.org/10.1016/j.ifacol.2017.08.362, 2-s2.0-85031810902.
10.1016/j.ifacol.2017.08.362
Google Scholar
31 Mu B., Ren J., and Yuan S., An efficient approach based on the gradient definition for solving conditional nonlinear optimal perturbation, Mathematical Problems in Engineering. (2017) 2017, 10, 3208431, https://doi.org/10.1155/2017/3208431.
10.1155/2017/3208431
Web of Science® Google Scholar

Citing Literature

All articles

FPGA Implementation of an Improved Reconfigurable FSMIM Architecture Using Logarithmic Barrier Function Based Gradient Descent Approach

Abstract

1. Introduction

2. Problem Formulation

3. Methodology

3.1. State Assignment Using Logarithmic Barrier Function Based Gradient Descent Approach for the Reconfigurable FSM

3.2. An Illustrative Example for the Improved Reconfigurable FSMIM Architecture

4. Numerical Results and Discussions

5. Concluding Remarks

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

FPGA Implementation of an Improved Reconfigurable FSMIM Architecture Using Logarithmic Barrier Function Based Gradient Descent Approach

Abstract

1. Introduction

2. Problem Formulation

3. Methodology

3.1. State Assignment Using Logarithmic Barrier Function Based Gradient Descent Approach for the Reconfigurable FSM

3.2. An Illustrative Example for the Improved Reconfigurable FSMIM Architecture

4. Numerical Results and Discussions

5. Concluding Remarks

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information