This paper proposes a photovoltaic (PV) power system for battery charger applications. The charger uses an interleaving boost converter with a single-capacitor turn-off snubber to reduce voltage stresses of active switches at turn-off transition. Therefore, active switches of the charger can be operated with zero-voltage transition (ZVT) to decrease switching losses and increase conversion efficiency. In order to draw the maximum power from PV arrays and obtain the optimal power control of the battery charger, a perturbation-and-observation method and microchip are incorporated to implement maximum power point tracking (MPPT) algorithm and power management. Finally, a prototype battery charger is built and implemented. Experimental results have verified the performance and feasibility of the proposed PV power system for battery charger applications.

1. Introduction

Due to the continuous growth of the global energy demand for developing industry, it increases society awareness of environmental impacts from the widespread utilization of fossil fuels, leading to the exploration of renewable energy sources, such as PV arrays, wind energy, and so on. One of these sources is PV arrays energy, which is clean, quiet, and maintenance-free. However, due to the instability and intermittent characteristics of PV arrays, it cannot provide a constant or stable power output. Thus, a power converter (dc/dc converter or dc/ac converter) and MPPT algorithm are required to regulate its output power.

Several MPPT algorithms have been proposed [1–10]. Some of the popular MPPT algorithms use perturbation-and-observation method [1–3], incremental conductance method [4], constant voltage method [5, 6], β method [7], system oscillation method [8, 9], and ripple correlation method [10]. The perturbation-and-observation method requires the measurement of only a few parameters, thus it facilitates an MPPT control. As a result, it is often applied to the PV arrays for enhancing power capacity.

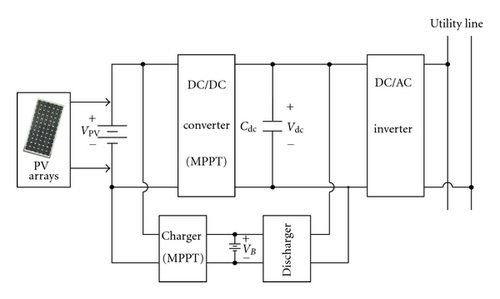
A typical PV power system is shown in Figure 1. The PV arrays usually need a battery charger to increase its utility rate. The research of this paper is only focused on PV arrays for battery charger applications. For charger design, many charging methods have been developed, such as the constant trickle current (CTC), constant current (CC), constant voltage (CV), hybrid CC/CV [11], and reflex charging methods [12–15]. The CTC method has a disadvantage that it has a longer charging time, the CC and CV are the simplest methods to battery charger, but both of them result in the situations of undercharge and overcharge. The hybrid CC/CV method can improve charging efficiency and charging time, but it has a disadvantage of difficult control. To reduce the charging time of the batteries, the reflex charging method is adopted in this paper. The method consists of a high positive pulse-charging current followed by a high current, short time negative pulse-discharging current, and a rest period. A high positive pulse-charging current can reduce the charging time and a negative pulse-discharging current is to reduce internal cell pressure and temperature of batteries. A rest period can provide the batteries with a reflex time in charging process.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Block diagram of a typical PV power system.

The basic switching power converters have six circuit structures, such as buck, boost, buck-boost, Cuk, Sepic, and Zeta converters. In order to obtain continuous input current for battery charger, the basic boost converter is widely used. However, it is operated under high switching frequencies resulting in high switching losses, noises, and component stresses. These drawbacks reduce power seriously and deteriorate in the performances of the basic boost converter. In order to alleviate the problems described previously, soft-switching technologies are introduced into the basic boost converter to reduce switching losses. Soft-switching technologies can be classified as passive and active soft-switching technologies. The passive technologies use only passive components to perform soft-switching operation [16–18]. The active technologies add one or more active switches along with other passive components to the basic switching power converters to perform soft-switching operation [19, 20]. For cost considerations, the proposed battery charger with passive soft-switching technologies is more attractive at low power level applications.

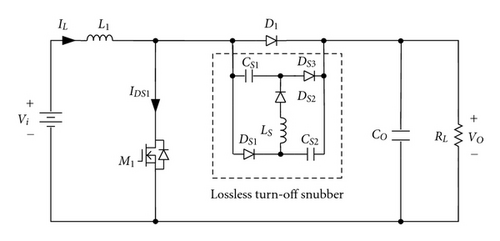
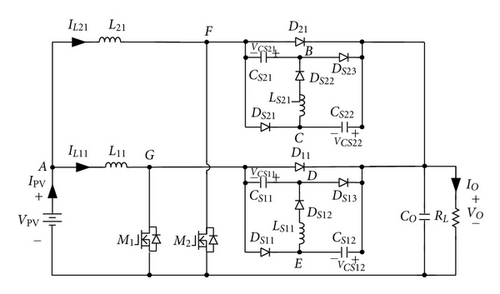
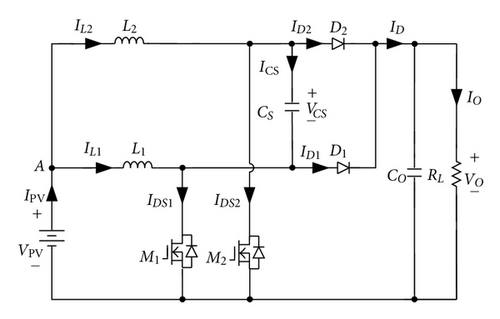
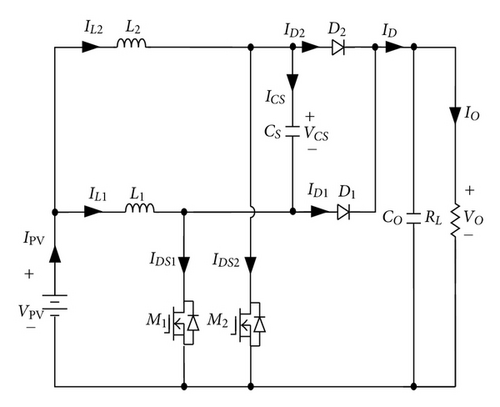
A basic boost converter with a passive lossless turn-off snubber for battery charger applications is usually adopted, as shown in Figure 2 [18], because it has a simple structure. However, the basic boost converter has a disadvantage that its output ripple current will swing over a wide range resulting in a low battery life. In order to reduce output ripple current and increase power level, two sets of boost converters are incorporated with an interleaving fashion, as shown in Figure 3 [21]. Although interleaving boost converter with two sets of passive soft-switching circuits can also achieve soft-switching features, their component counts and cost are increased significantly. To overcome the previously discussed drawbacks, an interleaved boost converter with a single-capacitor turn-off snubber for battery charger applications is proposed, as shown in Figure 4. The proposed battery charger requires only a resonant capacitor C_S which is associated with inductors L₁ and L₂ to reduce switching losses of active switches.

2. Control Algorithm of the Proposed Charger

In order to achieve an optimal power control of battery charger, an MPPT algorithm and a power management unit are needed. These control algorithms are described as follows.

2.1. Topology of Battery Charger

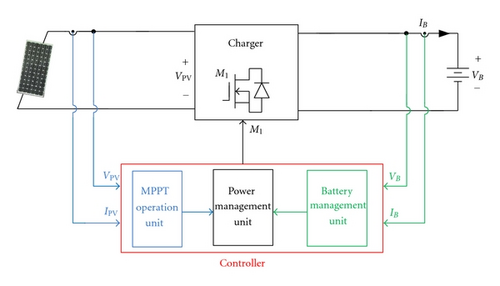
The proposed charger includes an interleaving boost converter and a controller, as shown in Figure 5. Moreover, the controller adopts microchip to implement MPPT of PV arrays and battery charging management. Therefore, the controller of the proposed battery charger can be divided into three units. They are MPPT operation, battery management, and power management units. The MPPT operation unit can implement the MPPT of PV arrays. The charging algorithm of battery charger is controlled with reflex charging method by battery management unit to reduce the charging time. In order to achieve the best energy utilization of the PV arrays, an MPPT with perturbation-and-observation method is integrated into an MPPT operation unit. Since the MPPT and charging algorithm must be associated to implement optimal control of battery charger, the power management unit is needed. To achieve optimal stability and safety for the proposed battery charger, the functions of under-voltage, over-current, and over-temperature protection circuits are required. All of the protection signals are also realized on a microchip.

2.2. MPPT Algorithm

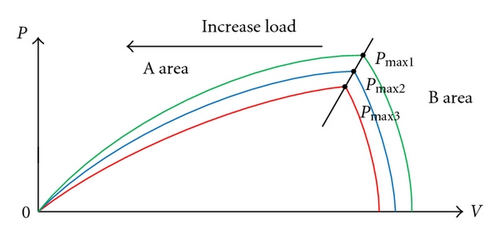
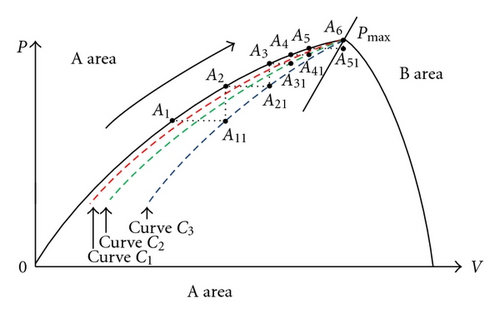
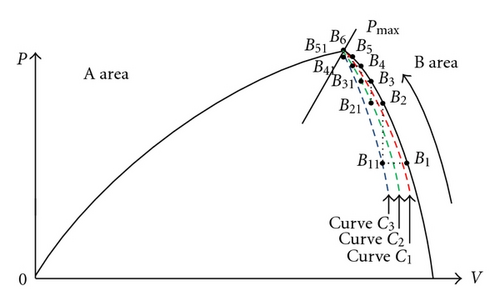
Output characteristic variations of PV array depend on climatic conditions, such as temperature of PV arrays and insolation of sun. Its P-V curves at different insolation of the sun are shown in Figure 6. From Figure 6, it can be seen that each insolation level has a maximum power P_max, where P_max 1 is the maximum power at the largest insolation of sun while P_max 3 is the one at the least insolation of sun. Three maximum power points P_max 1 ~ P_max 3 can be connected by a straight line. Operational area on the right hand side of the straight line is defined as B area, while the one on the left hand side is defined as A area. Since output load connected in PV arrays increases, output voltage of PV arrays decreases. Therefore, when working point of PV arrays locates in A area, output load must decrease to make the working point to approach the maximum power point of PV arrays. On the other hand, when working point of PV arrays places on B area, output load must increase. Their operation conditions are shown in Figure 7. Figure 7(a) shows the working point located on A area, while Figure 7(b) illustrates the one located on B area. When working point locates on A area, the working point is changed from A₁ to maximum power point P_max at point A₆ through A₂, A₃, A₄, and A₅, as shown in Figure 7(a). When working point locates on B area, the working point is changed from B₁ to maximum power point P_max at point B₆ through B₂, B₃, B₄, and B₅, as shown in Figure 7(b). According to different operational area to increase or decrease output load, working point of PV arrays can be shifted to MPP.

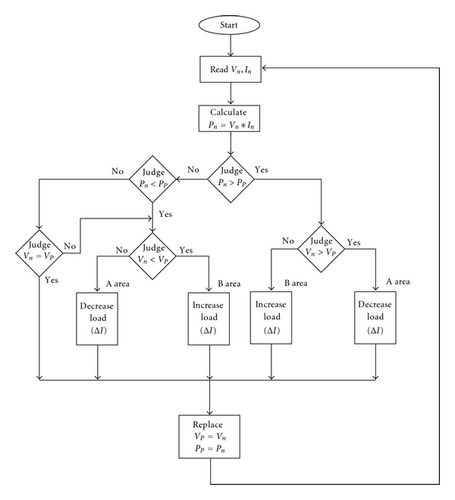
In order to extract maximum power of PV arrays, a simple perturbation-and-observation method is adopted. Its flow chart is shown in Figure 8. In the MPPT flow chart, V_n and I_n are, respectively, new voltage and current of PV arrays, V_P and P_P separately represent its old voltage and power value, and P_n( = V_n I_n) is the new power value of PV arrays. According to flow chart of MPPT using perturbation- and observation-method, the first step is to read new voltage V_n and current I_n of PV arrays, and then to calculate new PV power P_n. The next step is to judge the relationship of P_n and P_P. According to the relationship of P_n and P_P and procedures of MPPT flow chart, the procedure enters to judge the relationship of V_n and V_P. When the relationship of V_n and V_P is decided, operational area of working point can be specified. According to control algorithm of MPPT, when the working point of PV arrays is located in A area, power system connected in PV arrays to supply load power must decrease output power to close the distance between working point and MPP of PV arrays. On the other hand, when the operating point is located in B area, PV power energy must be increased to approach maximum power point of PV arrays. Finally, the procedure of MPPT flow chart is returned to the first step to judge next maximum power point of PV arrays.

2.3. Power Management

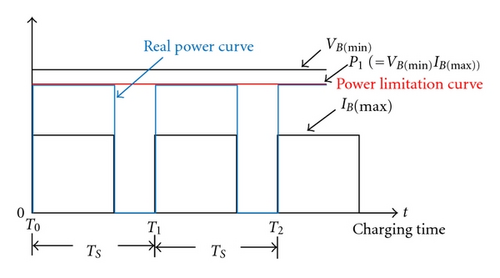
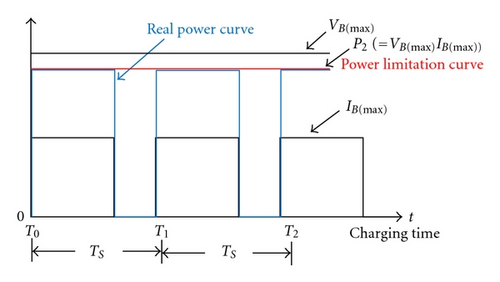
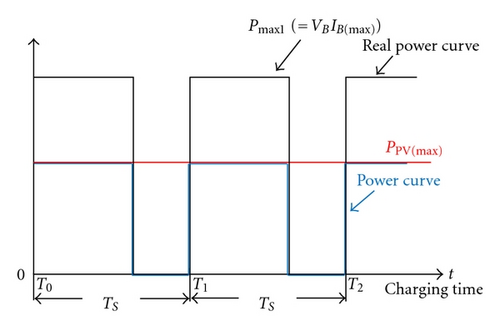
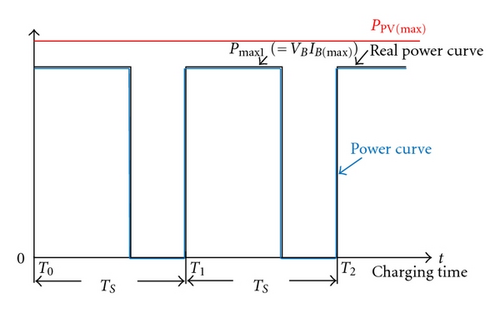
The proposed charger is with a reflex charging method to reduce charging time, since the charging voltage and current of batteries must be limited for protecting battery life. The conceptual waveforms of charging current and voltage of battery charger with a reflex charging method are shown in Figure 9. Figure 9(a) shows reflex charging waveforms of battery charger under minimum battery voltage V_B(min ), its V_B(min ) is expressed as undercharge condition of battery voltage. Figure 9(b) shows reflex charging waveforms of battery charger under maximum battery voltage V_B(max ), its V_B(max ) is expressed as overcharge condition of battery voltage. According to V_B(min ) and I_B(max ) or V_B(max ) and I_B(min ), the power limitation curve of battery charger can be obtained, as shown in Figure 9. When the maximum power P_PV(max ) of PV arrays is larger or less than P_max 1, the power operation point of PV arrays is traced as shown in Figure 10. As mentioned previously, the charging and discharging power of the proposed charger will be limited by power curve to extend battery life.

3. Derivation and Operational Principle of the Proposed Charger

In order to describe the merits of the proposed battery charger, its topology derivation and operational principles are briefly described as follows.

3.1. Derivation of the Proposed Charger

To reduce switching losses, a lossless turn-off snubber is inserted in a basic boost converter as shown in Figure 2. When switch M₁ is turned on, capacitors C_S1 and C_S2 are charged through inductor L_s and diode D_S2 in a resonant manner. At the end of the resonant interval, capacitors C_S1 and C_S2 are charged to V_O and are clamped at V_O until switch M₁ is turned off. When switch M₁ is turned off, the charges stored in capacitors C_S1 and C_S2 are discharged to output load through diodes D_S1 and D_S3, respectively. Thus, switch M₁ is turned off with zero-voltage transition (ZVT). As mentioned previously, although it can achieve the soft-switching feature, its output current ripple is relatively large for high current and low output voltage applications. Therefore, to reduce output current ripple, an interleaving scheme is usually adopted. In the following, the proposed interleaving boost converter with a single-capacitor snubber is derived.

Two lossless turn-off snubbers are used in an interleaving boost converter to reduce switching losses, as shown in Figure 3. To simplify circuit of Figure 3, voltages of capacitors C_S12 and C_S22 are replaced with dc voltages and , respectively. When voltages of capacitors C_S12 and C_S22 are replaced with dc voltages, the energies stored in capacitors C_S12 and C_S22 do not need to discharge their charges. Thus, diodes D_S11 and D_S21 can be removed, as shown in Figure 11(a). If voltage V_CS12 or V_CS22 is equal to (V_O–V_PV), nodes A, C, and E will have the same potential. Thus, they can be merged as node A, as shown in Figure 11(b). Based on the operational principle of an interleaving boost converters and the turn-off snubber, operational states of diode D₁₁ (or D₂₁) is the same as diode D_S23 (or D_S13) except that the operational duration of the turn-off snubber is operated within resonant mode. Since the duration of resonant mode is much shorter than a period of the proposed converters, nodes F and D (or G and B) can be combined as the same node H (or I), as shown in Figure 11(c). It will not affect its original operational principle. Because inductor currents I_L11 and I_L21 are unidirectional in the derived converter, inductors L₁₁ and L_S21 connected with diode D_S22 in series can be combined and replaced by inductor L₁. Similarly, inductors L₂₁ and L_S11 and diode D_S12 can be also merged as inductor L₂, as shown in Figure 11(d). In Figure 11(c), since capacitors C_S11 and C_S21 and diodes D₁₁ and D_S23 or D₂₁ and D_S13 are, respectively, connected in parallel, they can be, respectively, incorporated as capacitor C_S and diode D₁ or D₂. From Figure 11(d), it can be observed that the derived boost converter requires only a resonant capacitor C_S, which is associated with inductors L₁ and L₂ to function as a lossless turn-off snubber, reducing switching losses and component counts significantly. Therefore, Figure 11(d) is proposed for battery charger applications.

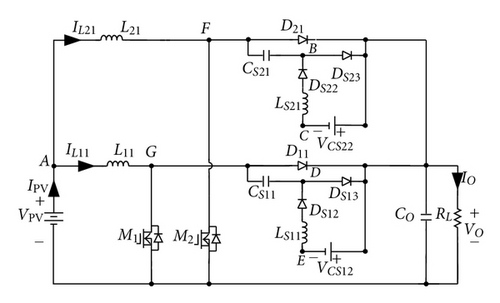
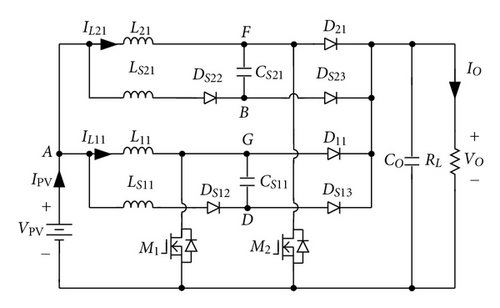
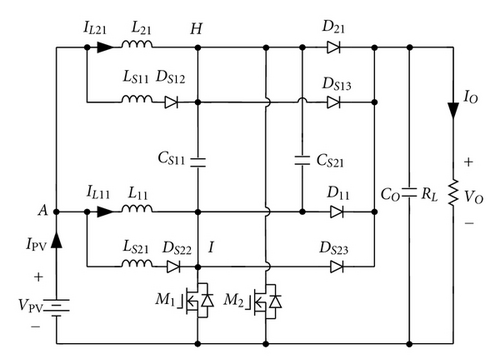
3.2. Operational Principle of the Proposed Charger

In Figure 4, the proposed battery charger with a single-capacitor turn-off snubber can achieve a ZVT feature for active switches. Operational modes of the proposed charger are divided into ten modes, as illustrated in Figure 12, and their key waveforms are illustrated in Figure 13. In the following, each operational mode is described briefly.

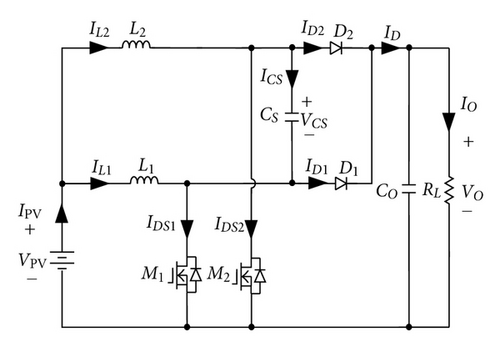
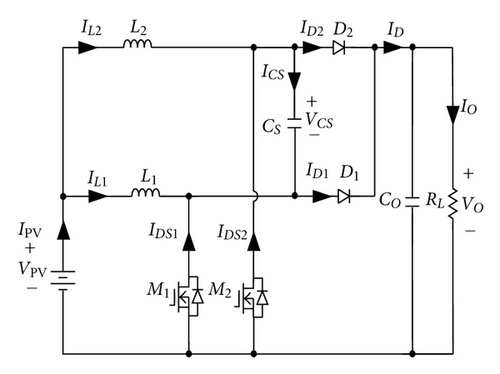
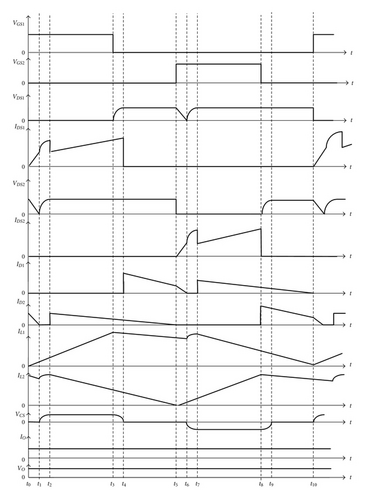
Mode 1 (Figure 12(a); t0 ≤ t < t1). Before t₀, diode D₂ is in freewheeling, and inductor current I_L2 is equal to diode current I_D2. At t = t₀, switch M₁ is turned on. The equivalent circuit at this time interval is shown in Figure 12(a), from which it can be found that switch current is equal to the sum of capacitor current I_CS and inductor current I_L1. Since the interval of t₀ ~ t₁ is very short, inductor current I_L1 is approximately equal to zero and capacitor voltage V_CS is close to zero. Thus, switch current I_DS1 is approximately equal to capacitor current I_CS. During this time interval, the current I_CS is abruptly increased up to inductor current I_L2, and I_D2 is abruptly decreased down to zero.

Mode 2 (Figure 12(b); t1 ≤ t < t2). At time t₁, capacitor current I_CS is equal to inductor current I_L2, and diode D₂ is reversely biased. At this time interval, snubber capacitor C_S resonates with inductor L₂, and switch current I_DS1 is just equal to the sum of resonant inductor current I_L2( = I_CS) and inductor current I_L1. At the same time, capacitor current I_CS reaches its maximum value which can be expressed as follows:

()

where Z_O is the characteristic impedance of L₂-C_S or L₂-C_S network, which is equal to

Mode 3 (Figure 12(c); t2 ≤ t < t3). When t = t₂, capacitor voltage V_CS is equal to V_O, and diode D₂ starts freewheeling through inductor L₂. At the same time, switch M₁ is still in the on state. The switch current I_DS1 is now equal to inductor current I_L1 which increases linearly, while inductor current I_L2 is decreased linearly.

Mode 4 (Figure 12(d); t3 ≤ t < t4). At time t₃, switch M_l is turned off. Because inductor current I_L1 must be continuous, capacitor C_S starts to discharge for sustaining a continuous inductor current. Thus, switch M₁ can be turned off with ZVT.

Mode 5 (Figure 12(e); t4 ≤ t < t5). When time reaches t₄, the voltage V_CS across capacitor C_S is discharged toward zero, and diode D₁ starts freewheeling. During this time interval, diodes D₁ and D₂ are in freewheeling through inductors L₁ and L₂, respectively.

Mode 6 (Figure 12(f); t5≤ t < t6). At time t₅, diode D₁ is still in freewheeling, but diode D₂ stops freewheeling because inductor current I_L2 drops to zero. In this moment, switch M₂ is turned on. Inductor current I_L1 is equal to the sum of diode current I_D1 and capacitor current −I_CS. Additionally, because the switch current will flow through the low-impedance path of capacitor C_S, diode current I_D1 will be dominated by the switch current . That is, within this time duration, capacitor current −I_CS is approximately equal to the switch current I_DS2. Capacitor current −I_CS is abruptly increased up to inductor current I_L1, and I_D1 is abruptly decreased down to zero.

Mode 7 (Figure 12(g); t6 ≤ t < t7). At time t₆, diode D₁ is reversely biased, and resonant network formed by capacitor C_S and inductor L₁ starts resonating. The switch current I_DS2 is equal to the sum of inductor current I_L1 ( = −I_CS) and inductor current I_L2 , and capacitor C_S is reversely charged.

Mode 8 (Figure 12(h); t7 ≤ t < t8). At t = t₇, the capacitor voltage V_CS goes down to −V_O. The time interval lasts approximately a quarter of the resonant cycle. At the same time, capacitor current −I_CS reaches its maximum value, which can be expressed by (1). During this mode, diode D₁ starts freewheeling, and inductor current I_L2 is increased linearly.

Mode 9 (Figure 12(i); t8 ≤ t < t9). At time t₈, switch M₂ is turned off. Since the inductor current I_L2 must be in smooth transition, capacitor voltage will drop to maintain a continuous inductor current. When t = t₉, capacitor voltage V_CS drops to zero.

Mode 10 (Figure 12(j); t9 ≤ t < t10). During this time interval, diodes D₁ and D₂ are in freewheeling through inductors L₁ and L₂, and their currents I_D1 and I_D2 are decreased linearly. When switch M_l is turned on again at the end of Mode 10, a new switching cycle will be recycled.

4. Control and Design of the Proposed Charger

In order to achieve optimal control of the proposed charger, the MPPT operation algorithm of PV arrays and reflex charging algorithm of battery must be considered. In the following, control and design of the proposed charger are described.

4.1. Control of the Proposed Charger

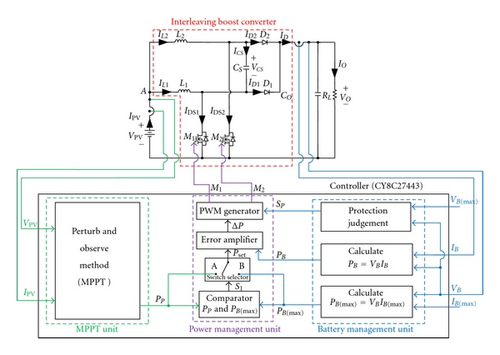
The proposed charger consists of an interleaving boost converter and controller. The controller adopts microchip of CY8C27443 made by Cypress Company. Block diagram of the proposed charger is shown in Figure 14. In Figure 14, the CY8C27443 microchip is divided into three units: MPPT, battery management, and power management units. In MPPT unit, the perturbation-and-observation method is adopted to trace maximum power point of PV arrays. The maximum power P_P of PV arrays can be decided. Moreover, battery management unit has four input signals (V_B, V_B(max ), I_B, and I_B(max )) where V_B is the battery voltage, V_B(max ) is the set maximum battery voltage, I_B is the battery charging current, and I_B(max ) is the set maximum battery charging current. According to four input signals, P_B( = V_B I_B) and P_B(max )( = V_B I_B(max )) can be calculated. The P_B represents the present charging power of battery, while P_B(max ) is the set maximum charging power. In addition, when V_B is equal to or greater than V_B(max ), protection judgment makes output signal S_P from low to high value. The S_P is sent to PWM generator for shutdown PWM generator to avoid battery overcharge. In power management unit, a comparator is used to judge relationship of P_P and P_B(max ). When P_P(=P_PV(max )) is greater than P_B(max ), signal S₁ is high and switch selector is operated to set P_set = P_B(max ). When P_P is equal to or less than P_B(max ), signal S₁ is low and switch selector is operated to set P_set = P_B. The P_set and P_B are sent to error amplifier to attain error value ΔP. When PWM generator attains ΔP, ΔP and triangle waves inside PWM generator attain PWM signals M₁ and M₂ via the comparator. The interleaving boost converter can change charging current I_B according to PWM signals M₁ and M₂.

4.2. Design of the Proposed Charger

To realize the proposed soft-switching charger systematically, design of inductor L₁ or L₂ and the snubber C_S are presented as follows.

4.2.1. Design of Inductor L₁ or L₂

Since the proposed charger is operated at the boundary of continuous conduction mode (CCM) and discontinuous conduction mode (DCM), the relationship between V_i and V_O can be attained with volt-second balance principle. Thus, transfer function M( = V_O/V_PV) can be expressed as

()

where D is duty ratio of the proposed charger. When duty ratio D is determined by the relationship between V_PV and V_O, inductor L₁ or L₂ can also be expressed as

()

where T_S is the switching cycle of the proposed charger and I_O is output current.

4.2.2. Design of Snubber Capacitor C_S

In the proposed charger, capacitor C_S resonates with inductor L₁ or L₂ to smooth out switch voltage at turn-off transition. The energy stored in C_S can be determined as

()

To completely eliminate the switch turn-off loss, the energy stored in capacitor C_S must be at least equal to the turn-off loss W_Soff. According to switching loss calculation of switch, W_Soff can be expressed by

()

where t_Soff is the falling time of switch at turn-off transition, V_O represents output voltage and I_DP is switch current at turn-off transition of switch. Therefore, capacitor C_S can be determined as

()

The peak current I_CS of capacitor C_S should be limited to being less than the peak values of I_DS1 and I_DS2, so it will not increase the current ratings of switches M₁ or M₂. To eliminate turn-off loss W_Soff completely at different operation conditions, the time t_Soff is approximately equal to 200 ns in practical design considerations.

5. Measurements and Results

To verify the analysis and discussion, a PV system used to charge 48 V battery with the following specifications was implemented:

(i)
input voltage V_i: 34 ~ 42V_dc (PV arrays),
(ii)
output voltage V_O: 44 ~ 54 V_dc (4 sets of 12 V battery connected in series),
(iii)
output maximum current I_O(max ): 10 A,
(iv)
output maximum power P_O(max ): 540 W.

From (6), value of snubber capacitor C_S can be calculated as 37 nF where I_DP is 10 A and V_O is 54 V. In our design sample, a capacitor with 39 nF is adopted. The components of power stage in the proposed boost converters are determined as follows:

(i)
M₁, M₂: IRFP250,
(ii)
D₁, D₂: MVUR1560,
(iii)
C_O: 470 μF,
(iv)
L₁, L₂: 30 μH,
(v)
C_S: 39 nF,
(vi)
inductor core: EE-35.

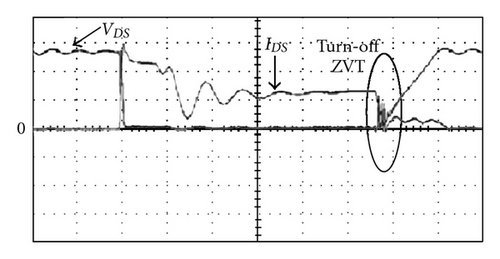
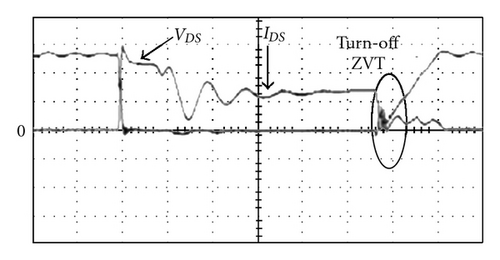
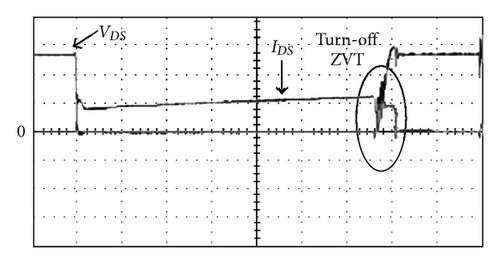
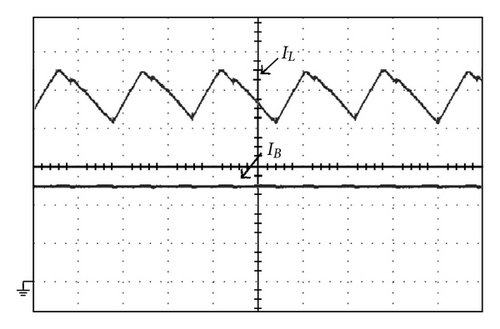
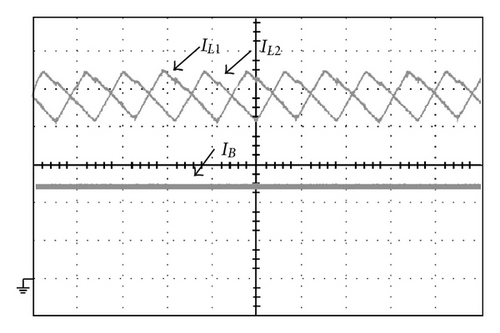
The measured voltage and current waveforms of the active switches with the proposed single-capacitor snubber (as shown in Figure 4) and with two sets of turn-off snubbers (as shown in Figure 3) are shown in Figures 15 and 16, respectively. Although we can observe that each power switch is turned off with ZVT feature, there still exist significant differences. Compare with Figures 15 and 16, we can see that the rise voltage curves of Figure 15 are smoother than those of Figure 16. The reason of this is that interleaving boost converter with two sets of turn-off snubbers, causes an abrupt energy on active switches and results in more switching losses. Figure 17(a) shows measured inductor current and charging current of the single boost converter with a turn-off snubber, and Figure 17(b) shows measured inductor current and charging current of the proposed interleaved boost converter with a single-capacitor turn-off snubber. From Figure 17, it can be seen that the proposed converter with a single-capacitor turn-off snubber has a lower ripple charging current I_B.

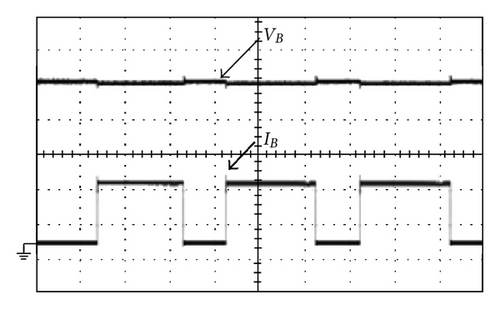
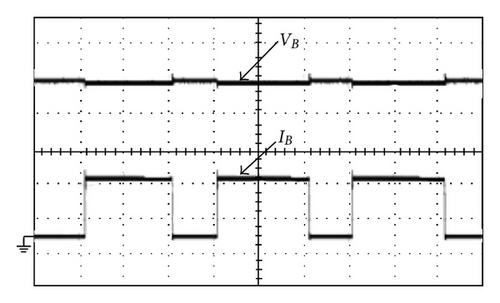
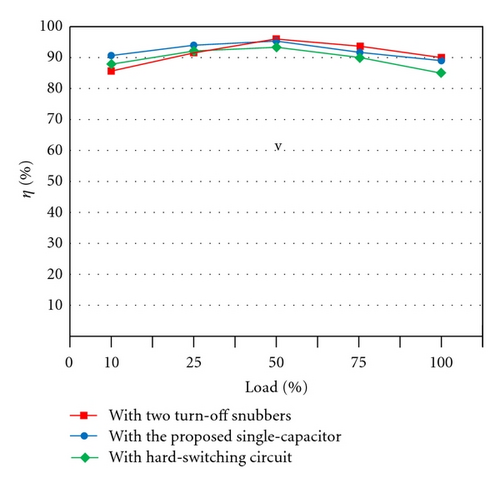
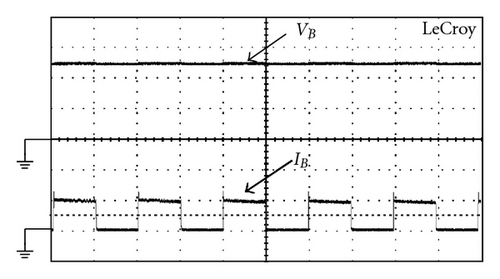
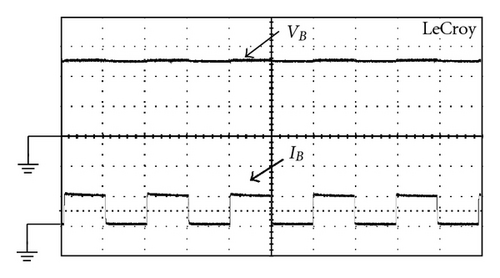
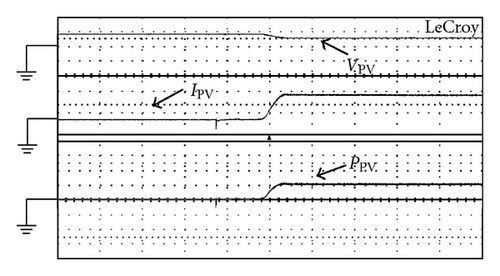
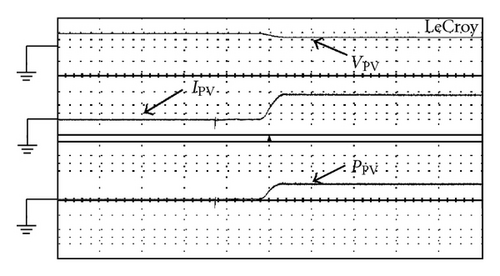
To make a fair comparison, the hardware components of the proposed charger and hard-switching boost charger are kept as the same as possible. Figure 18 shows the plots of output voltage and current waveforms of the two kinds of chargers under step-load changes between 20% and 100% with, respectively, rate of 1 kHz and a duty ratio of 50%. From Figure 18, it can be observed that although the proposed charger uses less component counts, it yields almost the same dynamic performance as those with complicated configurations. The comparisons between the efficiencies of the proposed charger and their counterparts are illustrated in Figure 19. It can be observed that the proposed charger cannot always yield higher efficiencies than the others under various operating conditions. It has a trend that, at higher output load, the proposed charger and the ones with two turn-off snubbers can yield higher efficiency, while at lower ones, the discussed charger with two sets of turn-off snubbers yields lower efficiency than the others. The reasons behind this are that at a fixed power level, a higher output load level will result in higher switch currents and the turn-off losses W_Soff will be much higher than the sum of the extra conduction loss W_ES and switching loss W_Son. Figure 20 shows the measured waveforms of battery voltage V_B and charging current I_B with pulse current charging method under repetitive rate of 1 s and duty ratio of 500 ms, as shown in Figure 14. Figure 20(a) shows those waveforms under P_PV(max ) = 50 W, while Figure 20(b) illustrates those waveforms P_PV(max ) = 100 W. From Figure 20, it can be seen that maximum pulse charging current I_O(max ), respectively, is limited 1 A (about 0.15 C) and 2 A (about 0.3 C), where battery adopts lead-acid battery and capacity of each battery is 12 V/7 Ah and total battery voltage is 50 V. Measured waveforms of voltage V_PV, current I_PV and power P_PV of PV arrays with perturbation-and-observation method are used to implement MPPT. Figure 21(a) shows those waveforms under maximum power point P_PV(max ) at 100 W, while Figure 21(b) depicts those waveforms under P_PV(max ) at 200 W. From Figure 21, it can be found that tracking time of PV arrays from zero to the maximum power point is about 40 ms.

6. Conclusions

In this paper, an interleaving boost converter with a passive snubber for battery charger applications is proposed. The proposed charger with a single-capacitor snubber to reduce voltage stresses of active switches at turn-off transition. Therefore, the conversion efficiency of the proposed charger can be increased significantly. In order to draw maximum power from the PV energy, a simple perturbation-and-observation method is incorporated to realize maximum power conversion. To verify the merits of the proposed charger, the operational principle, steady-state analysis, and design considerations have been described in detail. Additionally, from the experimental efficiency of the proposed charger, it has been shown that the proposed charger can yield higher efficiency at heavy load condition. An experimental prototype for a battery charger application (540 W, 54 V_dc/10 A) has been built and evaluated, achieving the efficiency of 88% under full load condition. Therefore, the proposed interleaving boost converter is relatively suitable for battery charger applications.

References

1 Brunton S. L., Rowley C. W., Kulkarni S. R., and Clarkson C., Maximum power point tracking for photovoltaic optimization using ripple-based extremum seeking control, IEEE Transactions on Power Electronics. (2010) 25, no. 10, 2531–2540, 2-s2.0-77957730666, https://doi.org/10.1109/TPEL.2010.2049747.
10.1109/TPEL.2010.2049747
Web of Science® Google Scholar
2 Agarwal V., Aggarwal R. K., Patidar P., and Patki C., A novel scheme for rapid tracking of maximum power point in wind energy generation systems, IEEE Transactions on Energy Conversion. (2010) 25, no. 1, 228–236, 2-s2.0-77950690809, https://doi.org/10.1109/TEC.2009.2032613.
10.1109/TEC.2009.2032613
PubMed Web of Science® Google Scholar
3 Subiyanto A. M. and Hussain S., Hopfield neural network optimized fuzzy logic controller for mximum power point tracking in a photovoltaic system, International Journal of Photoenergy. (2012) 2012, 13, 798361, https://doi.org/10.1155/2012/798361.
10.1155/2012/798361
Web of Science® Google Scholar
4 Taherbaneh M., Rezaie A. H., Ghafoorifard H., Rahimi K., and Menhaj M. B., Maximizing output power of a solar panel via combination of sun tracking and maximum power point tracking by fuzzy controllers, International Journal of Photoenergy. (2010) 2010, 13, 2-s2.0-79955039583, https://doi.org/10.1155/2010/312580, 312580.
10.1155/2010/312580
Web of Science® Google Scholar
5 Weidong X. and Dunford W. G., A modified adaptive hill climbing MPPT method for photovoltaic power systems, 3, Proceedings of the IEEE 35th Annual Power Electronics Specialists Conference (PESC ′04), June 2004, 1957–1963, 2-s2.0-8744252386.
Google Scholar
6 Kobayashi K., Matsuo H., and Sekine Y., An excellent operating point tracker of the solar-cell power supply system, IEEE Transactions on Industrial Electronics. (2006) 53, no. 2, 495–499, 2-s2.0-33645707855, https://doi.org/10.1109/TIE.2006.870669.
10.1109/TIE.2006.870669
Web of Science® Google Scholar
7 Jain S. and Agarwal V., A new algorithm for rapid tracking of approximate maximum power point in photovoltaic systems, IEEE Power Electronics Letters. (2004) 2, no. 1, 16–19, 2-s2.0-2942711829, https://doi.org/10.1109/LPEL.2004.828444.
10.1109/LPEL.2004.828444
Google Scholar
8 Chung H. S. H., Tse K. K., Hui S. Y. R., Mok C. M., and Ho M. T., A novel maximum power point tracking technique for solar panels using a SEPIC or Cuk converter, IEEE Transactions on Power Electronics. (2003) 18, no. 3, 717–724, 2-s2.0-0038630873, https://doi.org/10.1109/TPEL.2003.810841.
10.1109/TPEL.2003.810841
Web of Science® Google Scholar
9 Ho B. M. T. and Chung H. S. H., An integrated inverter with maximum power tracking for grid-connected PV systems, APEC. (2004) 3, 953–962.
Google Scholar
10 Casadei D., Grandi G., and Rossi C., Single-phase single-stage photovoltaic generation system based on a ripple correlation control maximum power point tracking, IEEE Transactions on Energy Conversion. (2006) 21, no. 2, 562–568, 2-s2.0-33744530398, https://doi.org/10.1109/TEC.2005.853784.
10.1109/TEC.2005.853784
Web of Science® Google Scholar
11 Hussein A. A.-H. and Batarseh I., A review of charging algorithms for nickel and lithium battery chargers, IEEE Transactions on Vehicular Technology. (2011) 60, no. 3, 830–838, 2-s2.0-79952847905, https://doi.org/10.1109/TVT.2011.2106527.
10.1109/TVT.2011.2106527
Web of Science® Google Scholar
12 Savoye F., Venet P., Millet M., and Groot J., Impact of periodic current pulses on Li-Ion battery performance, IEEE Transactions on Industrial Electronics. (2012) 59, no. 9, 3481–3488, https://doi.org/10.1109/TIE.2011.2172172.
10.1109/TIE.2011.2172172
Web of Science® Google Scholar
13 Chen L. R., Design of duty-varied voltage pulse charger for improving Li-ion battery-charging response, IEEE Transactions on Industrial Electronics. (2009) 56, no. 2, 480–487, 2-s2.0-60449113247, https://doi.org/10.1109/TIE.2008.2002725.
10.1109/TIE.2008.2002725
CAS Web of Science® Google Scholar
14 Chuang Y. C. and Ke Y. L., High efficiency battery charger with a buck zero-current-switching pulse-width-modulated converter, Interactive Electronic Technical Specification. (2008) 1, 433–444, https://doi.org/10.1049/iet-pel:20070215.
10.1049/iet?pel:20070215
Google Scholar
15 Chen L. R., Young C. M., Chu N. Y., and Liu C. S., Phase-locked bidirectional converter with pulse charge function for 42-V/14-V dual-voltage PowerNet, IEEE Transactions on Industrial Electronics. (2011) 58, no. 5, 2045–2048, 2-s2.0-79954534579, https://doi.org/10.1109/TIE.2010.2051930.
10.1109/TIE.2010.2051930
Web of Science® Google Scholar
16 Yun J., Choe H.-J., Hwang Y.-H., Park Y.-K., and Kang B., Improvement of power-conversion efficiency of a DC—DC boost converter using a passive snubber circuit, IEEE Transactions on Industrial Electronics. (2012) 59, no. 4, 1808–1814.
10.1109/TIE.2011.2141095
Web of Science® Google Scholar
17 Gallo C. A., Tofoli F. L., and Pinto J. A. C., A passive lossless snubber applied to the ACDC interleaved boost converter, IEEE Transactions on Power Electronics. (2010) 25, no. 3, 775–785, 2-s2.0-77950800391, https://doi.org/10.1109/TPEL.2009.2033063.
10.1109/TPEL.2009.2033063
Web of Science® Google Scholar
18 Munoz C., Study of a new passive lossless turn-off snubber, CIEP. (1998) 147–152.
Google Scholar
19 Lin B. R. and Shih H. Y., ZVS converter with parallel connection in primary side and series connection in secondary side, IEEE Transactions on Industrial Electronics. (2011) 58, no. 4, 1251–1258, 2-s2.0-79952677927, https://doi.org/10.1109/TIE.2010.2042422.
10.1109/TIE.2010.2042422
Web of Science® Google Scholar
20 Wu T.-F., Chang Y.-D., Chang C.-H., and Yang J.-G., Soft-switching boost converter with a flyback snubber for high power applications, IEEE Transactions on Power Electronics. (2012) 27, no. 3, 1108–1119, https://doi.org/10.1109/TPEL.2011.2126024.
10.1109/TPEL.2011.2126024
Web of Science® Google Scholar
21 Luo Y. K., Su Y. P., Huang Y. P., Lee Y. H., Chen K. H., and Hsu W. C., Time-multiplexing current balance interleaved current-mode boost DC-DC converter for alleviating the effects of right-half-plane zero, IEEE Transactions on Power Electronics. (2012) 27, no. 9, 4098–4112, https://doi.org/10.1109/TPEL.2012.2188842.
10.1109/TPEL.2012.2188842
Web of Science® Google Scholar

Citing Literature

All articles

Photovoltaic Power System with an Interleaving Boost Converter for Battery Charger Applications

Abstract

1. Introduction