Long-term variability of the coastal ocean stratification in the Gulf of Naples: Two decades of monitoring the marine ecosystem at the LTER–MC site, between land and open Mediterranean Sea
Abstract
We analyze 20 years (2001–2020) of temperature and salinity profiles at the LTER–MC coastal station in the Gulf of Naples, Mediterranean Sea. Surface and bottom layers show weak increases of temperature ( and , 2005–2019); water-columns budgets (heat, freshwater) show pseudo-periodic oscillations every 3 to 5 years, and weak linear trends. Seasonal minimum of salinity occurs 2 months later than the runoff peak, pointing to the importance of horizontal circulation in regulating the inshore–offshore exchanges and the residence time of freshwater. Inter-annual variations of the mixed layer depth (MLD) indicate a shallowing ( during winter) and a shortened time span of the fully mixed water-column. A visible decadal shift in the external forcings suggests an influence of winterly wind stress in 2010–2019, that prevailed over dominant buoyancy fluxes in 2001–2009. Changes are visible in the large-scale indices of the North Atlantic and Western Mediterranean Oscillations and highlight the role of wind direction, offshore or inshore oriented, in disrupting the stratification driven by freshwater runoff. A Random Forest Regression confirms that role and quantifies the MLD's drivers importance. This allows for a reliable prediction of the stratification using external variables independent from the in-situ observations.
1 INTRODUCTION
Coastal areas represent of marine primary production (Smith et al., 2005), contribute to the largest portion of fish catches ( if we consider all Large Marine Ecosystems as coastal systems, Sherman et al., 2009), and provides for more than 90% of the global trade (WTO, 2018). While the latter is sustained by the crucial role of maritime transportation, the former strongly depend on physical processes that occur in coastal systems. Winds, runoff, tides, and heat fluxes (Ferrari & Wunsch, 2009) are the main source of auxiliary energy, sensu Margalef (1978) and Frontier et al. (2008), and modulate the large biogeochemical fluxes from land, through the atmosphere and runoff.
The presence and morphology of the land–ocean boundaries induce a high variability in abiotic and biotic components over spatial and temporal scales from daily to seasonal and inter-annual (Walsh, 1988). Organisms must adapt to this range of time scales over which the availability of resources vary. At mid and at high-latitudes, a prominent driver of the pelagic ecosystem is the seasonal cycle of the mixed layer (Sverdrup, 1953), even if the start of stratification is not the only trigger (Behrenfeld, 2010; Smetacek & Passow, 1990; Zingone et al., 2010). Further to this cycle, coastal currents (Lentz, 2012), eddies (Kersalé et al., 2013), and filaments (Iermano et al., 2012) may modify the vertical structure of stratification, even without significant upwelling. Analyzing the processes regulating the water-column structure in coastal ecosystems is therefore important, not only to assess the relative contributions of specific drivers in modulating the plankton dynamics depending on it, but also to attempt predicting how unique the seasonal and regional characterization of the local dynamics are (Sallée et al., 2021).
Here, the challenge is to characterize the regional dynamical regime and to determine how it would be affected by changes in climate and anthropogenic activities. The Mediterranean Sea is subject to warming and freshwater budget change (Bethoux et al., 1998; Borghini et al., 2014; Menna et al., 2022; Pisano et al., 2020), and events such as the 2003 heatwave have been associated with strong stratification and inhibited mixing (Olita et al., 2007). A general view indicates an increasing trend in the heat content of the basin in the last decades (Criado-Aldeanueva et al., 2012), with more frequent occurrences of heatwaves (Darmaraki et al., 2019). This emphasizes the question on how the Mediterranean Sea responds in various climate change scenarios for the next decades, whether it will be dominated by a basin-scale response to the global atmospheric adjustments, or driven more regionally by local river runoffs and atmospheric forcings (Adloff et al., 2015). In this context, an effort towards the development of climate indices and the improvement of long-term times series by in-situ observations is of importance, for both open and coastal areas. Both heat and saline content are important to monitor the climatic variations (Iona et al., 2018), but estimates of stratification from the water-column also have to be included to be compared to the observations in the upper 200 m during the recent decades (Guancheng et al., 2020) and to separate the roles of thermal and saline contents. The Mediterranean Sea is an important zone for attempting projections (Giorgi & Lionello, 2007), as it has been identified as a major ‘hotspot’ for exhibiting the effects of climate changes (Giorgi, 2006).
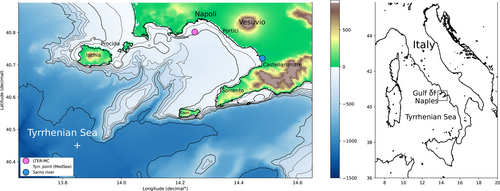
There are many studies on the complexity of unique regional configurations for diverse marine coastal systems. For example, the recent work of Xiu et al. (2018) illustrates the case of the California Current System, where wind and eddy activities in this specific area play a complex role in the redistribution and response of biological communities to nutrients supply. Each regional area is governed by specific physical and biogeochemical characteristics, establishing them as bioregions (El Hourany et al., 2021) whose variability evolves with global warming. Systems in a Mediterranean climate are expected to become warmer and drier with climate change, whereas estuaries in these regions are predicted to experience variability in freshwater flows, with consequences such as ‘marinisation’ and hypersaline conditions (Hallett et al., 2018). The Gulf of Naples (GoN) stands in this context. It is a coastal embayment opened to the Tyrrhenian Sea (Figure 1), with the Sarno river mouth on its South–West side, and the Volturno river flowing into the nearby Gulf of Gaeta. The surface circulation of the GoN is mainly driven by the local wind field, with the creation of specific patterns affecting both the physical and biological processes developing in the area (Cianelli et al., 2017). During winter months, predominant and most intense winds come from NNE and NE directions, which determine off-shore transport and sea storms (de Ruggiero et al., 2020; Menna et al., 2007; Saviano et al., 2021). In spring and autumn, the principal wind directions are NE and SW, the surface currents associated are characterized by the presence of recirculation structures, with both cyclonic and anticyclonic gyres at basin and sub-basin scales (Menna et al., 2007; Saviano et al., 2019; Saviano, Cianelli, et al., 2020). Finally, in summer, the setup and reinforcement of the Azore anticyclone, and in the latest years of the African anticyclone (Hatzaki et al., 2014) determine the onset of a stable, moderate breeze system with winds generally weaker than the rest of the year (Krauzig et al., 2020). This general wind regime is associated with numerous low pressure systems passing over the basin, with frequent stormy and windy events principally during winter and autumn (Saviano et al., 2022; Saviano, De Leo, et al., 2020). Importantly, the GoN is the site of a monitoring point, 2 km off the coast, sampled for more than 30 years as part of a LTER ( Long-Term Ecological Research ) national network.
In our study, we look at the evolution of the water-column structure over time to identify the physical processes whose sequence and interplay modulate the water-column stability and drive the local variability. Our analysis exploits the last 20 years of a time series of physical parameters from a 70 m water-column, using weekly CTD (Conductivity, temperature, and depth) profiles from January 2001 to February 2020. The stratification is described using the mixed layer depth (MLD), and in terms of surface-bottom gradient and by the relative contribution of temperature and salinity, providing a different point of view than the common mean-state description. Disentangling the different contributions of temperature and salinity to water buoyancy, we show the effect of climate on the warming and freshening. This is a result of changes in freshwater inputs, in a coastal environment such as the GoN, where modulations due to the ocean surface circulation are important. This allows us to establish the site as a good reference to project the impact of environmental forcing and anthropogenic activities on coastal systems and to differentiate the effects of each one. Specifically, here, we first describe the averaged seasonal climatological patterns, then the inter-annual variability, and focus in the third section on the seasonal drivers of the mixed layer in specific periods. To identify and assess the contribution of the relevant processes driving the mixed layer variability, external forcings such as wind stress and buoyancy fluxes are estimated over the area with the help of the ERA5 data set (ERA5: Fifth generation of ECMWF atmospheric reanalyses of the global climate, Copernicus Climate Change Service (C3S), 2017). Finally, we propose to use external forcings as a set of predictors of the mixed layer through a Random Forest Regression (RFR), to assess their relative weight and prepare for predictions in the following studies.
2 MATERIALS AND METHODS
A glossary of abbreviations and physical variables used in the text is available in Table 1.
| Acronym | Description | |
|---|---|---|
| GoN | Gulf of Naples | |
| LTER-MC | Long-term Ecological Research program (LTER) at the Marechiara coastal station (MC) | |
| MC# | Marechiara station number # | |
| CTD | Conductivity-Temperature-Depth | |
| ERA5 | ERA5: Fifth generation of ECMWF atmospheric reanalyses of the global climate | |
| MS | MedSea MFC physical reanalysis product | |
| ROMS | Regional Ocean Model System | |
| ML | Machine Learning | |
| RFR | Random forest regression |
| Variable | Description | Units |
|---|---|---|
| trend of X | per year | X/year |
| , or | Conservative temperature | °C |
| , or | Absolute salinity | g/kg |
| Seawater density | kg/m3 | |
| Potential density | kg/m3 | |
| Potential temperature | °C | |
| MLD | Mixed layer depth | m |
| HC | Heat content index | J/m2 |
| FW | Fresh water content index | cm |
| Buoyancy anomaly content index | kg/m2 | |
| Buoyancy anomaly content index from temperature | kg/m2 | |
| Buoyancy anomaly content index from salinity | kg/m2 | |
| IS | Intensity of stratification index | kg/m3 |
| Upper limit of salinity, above | S+ = 38.65 g/kg | |
| Maximum of salinity | Smax = 38.61 g/kg1 | |
| Net surface heat fluxes (latent + sensible heat + net solar + thermal radiation) | W/m2 | |
| or | Horizontal components of the wind velocity at 10 m | m/s |
| Wind direction from | Angular (°) | |
| Precipitation (P) and evaporation (E) rates | mm/day | |
| Significant wave height | m | |
| Buoyancy flux at the sea surface (here defined when stabilizing the water-column) | m2/s3, or W/kg | |
| Wind velocity friction at the sea surface | m/s | |
| NAO | North Atlantic Oscillation index | No units |
| WEMO | Western Mediterranean Oscillation index | No units |
2.1 Hydrological data set
The time series at the LTER–MC sampling point ( and ) in the Gulf of Naples (Figure 1) started in 1984 with a focus on biological sampling. The sampling frequency was biweekly until 1990, and weekly since 1995. A major interruption occurred from 1991 through February 1995. During the 1984–1990 period, the water-column was sampled at discrete depths (0, 2, 5, then 10–60 m every 10 m) using Niskin bottles equipped with reversing thermometers. Starting from 1995, continuous temperature and salinity profiles were obtained using different CTD (Conductivity, temperature, and depth) instruments, sometimes borrowed in the function of their availability, and some data lacked sparsely during the years due to weather or technical problems, mostly the lack of an institutional ship, since the ship used before sunk during a dramatic storm. Since 2001 the same instrument (Seabird SBE-911+) has been systematically used. For analysis consistency, to keep a constant sampling temporal coverage (weekly), a continuous vertical extent of the whole water-column, and the same data source, in our study, we consider the period from January 2001 to February 2020. CTD profiles were carried out with a Seabird SBE-911+ mounted on a 12-bottle Rosette sampler, with all sensors calibrated yearly. The raw 24 Hz profiles were processed using the standard Seabird software SeaSave to obtain bin-averaged data on a 1-m regular vertical grid. The weekly survey we use includes a total of 894 CTD profiles from 4 January 2001 (cast MC465) to 24 February 2020 (cast MC1359) (a calendar is available in Figure S1). The Gibbs Sea Water (GSW) Oceanographic Toolbox (McDougall & Barker, 2011) was used to calculate the conservative temperature (°C), the absolute salinity (g kg−1), the water density (kg m−3), the potential density (kg m−3), the potential temperature (°C), and the Brunt-Väisälä frequency (s−2). When mentioned thereafter, and refer to and , respectively. To provide a comparison in the surface between ocean coastal and open areas, we use time series of temperature and salinity with the MedSea (MS) data reanalysis product extracted at the entrance of the Gulf of Naples (see the location in Figure 1). The MS physical reanalysis product (Escudier et al., 2020) is generated by a numerical system composed of a hydrodynamic model, supplied by the Nucleus for European Modelling of the Ocean (NEMO) and a variational data assimilation scheme (OceanVAR) for temperature and salinity with a horizontal grid resolution of (i.e., 4–5 km) (https://resources.marine.copernicus.eu/product-detail/MEDSEA_MULTIYEAR_PHY_006_004/INFORMATION).
2.2 Water-column analysis: mixed layer depth, stratification contents, and budgets of heat and freshwater
Mixed layer depth (MLD, in m) was calculated following the method of de Boyer Montégut et al. (2004) based on threshold values. Given a vertical profile of density , or potential temperature , we subtract the value at m (reference value) from the profile, we calculate the cumulative sum from to the end of the profile, and we find the depth where the profile reached a threshold of 0.03 kg/m3 (if considering ), or 0.4°C (if considering ). To describe the stratification, a buoyancy anomaly content BC is calculated as the integral over depth of the density difference between each depth and the bottom: (kg/m2). The relative contributions of and to the buoyancy content is quantified as , with , and , where , and are the thermal expansion and saline contraction coefficients calculated with the GSW functions. We provide another complementary index to the buoyancy anomaly content, the stratification intensity IS, defined as the difference between the surface and bottom for each CTD profile: . We considered the MLD as the identifier of the depth at the top of the vertical gradient (in density, or temperature). This allowed us to divide the water-column in an upper homogeneous and a lower/deeper layer, including the gradient itself and, sometimes, a homogeneous deeper part. Due to the shallow depth of the station, the latter is not a recurrent feature during the stratified season. This also allowed us to consider the layer down to the MLD as that where surface fluxes had been recently mixed and integrated over time. Then the MLD becomes a characteristic indicator of the air–sea interactions. Instead, we used the IS index as a simple estimation of the vertical gradient of density between the vertical boundaries of the water-column, thus providing a bulk indicator of the buoyancy amplitude between the surface and bottom. We also used the BC index, defined as an integration of the difference of density between the water parcels in the water-column and the bottom. It takes into account all the various vertical layers, and describes the stability state of the whole water-column, instead of only its boundaries. It provides an indicator of the water-column stability, relative to the bottom layer, that is considered the most stable. A heat content HC (J/m2) and fresh water content FW (meter) are calculated for each CTD profile as (J m−2), (meter). Here dz = 1 m, zbottom = 65 m, and zsurface = 3 m, the maximum and shallowest depth common to all profiles, is the in-situ density (kg/m3), is the specific heat capacity (J/kg/°C) calculated with the GSW functions (McDougall & Barker, 2011). Here HC is not defined as a variation of heat from a reference value for the area and cannot be interpreted as an absolute value: it describes only the relative variations observed at this single monitoring point in the coastal area. FW gives the amount of fresh water in a meter that needs to be added to the water-column to decrease the absolute salinity value from to the observed depth-averaged salinity. The value provides a reference value of above the maximum value observed (at 10 m deep, cast MC1264, 29th August 2017).
2.3 Bulk parameters of the atmospheric forcings of the area: heat fluxes, precipitations, winds, and climatic indices
The net surface fluxes (, the total of latent and sensible heat, plus net solar and thermal radiation, in W/m2), wind velocities ( and , m/s), rates of evaporation and precipitation (mm/day), and significant wave height (, in W/m2), were extracted from the ERA5 re-analysed product provided by Copernicus (Copernicus Climate Change Service (C3S), 2017). The extraction is done at the closest grid-point from the LTER–MC geographic position, with a 6-h temporal resolution, from 1 January 2001 to 1 March 2020.
A seasonal cycle of the heat content from the surface fluxes (HF) is calculated by integrating each value of from (1st January 2001) to (1st March 2020) . HF represents the accumulated or absorbed heat, that will describe the seasonal cycle, with a part of the year when the water-column absorbs heat, and another part when heat is released.
Aside from these variables, daily river discharge around the GoN area was investigated using the historical data from the European Flood Awareness System provided by Copernicus (Mazzetti et al., 2019, https://cds.climate.copernicus.eu/cdsapp#!/dataset/efas-historical?tab=overview). A preliminarily study indicated that the variability of this product was very comparable to the precipitation rates, but difficult to relate directly to the in-situ time series, given the spatial spread of the freshwater sources along the coast and the lack of data about the GoN circulation during the period 2001–2020. We did not consider these data in our analysis, but we nevertheless provide their main characterizations in a dedicated section in Appendix S1 (the spatial distribution of the land freshwater sources, see Figure R1; their seasonal and inter-annual time series, see Figure R2).
The buoyancy flux (m2/s3, or W/kg, defined when is stabilizing the water-column), is proportional to the density flux at the surface: , where the density flux into the ocean from the atmosphere was computed as , with and the thermal expansion and saline contraction coefficients, respectively (Zhang & Talley, 1998). Here , and , where is the specific heat of seawater, , , and are the evaporation, precipitation, and sea surface salinity. The velocity friction was calculated as , where is the density of sea water, and the wind stress, as , where , and the drag coefficient 10 m is calculated following Large and Pond (1981).
The North Atlantic Oscillation (NAO) is responsible for changes in the geographic distribution of surface westerlies across the North Atlantic basin toward Europe (Hurrell, 1995), and we use the classic NAO index developed by Hurrell and Deser (2009) to describe these variations. Data were provided by the NOAA National Weather Service (https://www.cpc.ncep.noaa.gov/products/precip/CWlink/pna/nao.shtml). To link the Mediterranean basin dynamic to the Atlantic variability, we complete it with the Western Mediterranean Oscillation (WEMO), a pattern of atmospheric circulation described by Martin-Vide (2006), whose index corresponds to the difference in surface pressure between San Fernando (Spain) and Padua (Italy). Its variations can lead to a regime of winds blowing from the east (Bonifacio et al., 2019, e.g., case of the central European anticyclone located north of Italy, with a low-pressure center in the Iberian peninsula). Data were collected from http://www.ub.edu/gc/English/wemo.htm.
2.4 Temporal averaging and statistical fits
Property averages are calculated for different periods. The LTER–MC observations are made weekly: the day of the week for sampling depended on the sea and weather conditions, and was not necessarily the same (for example, MC465 was on Thursday, 4 January 2001, MC466 on Wednesday 10th, and MC467 on Tuesday 16th). To have the consistency of a regular temporal grid, we consider the week of the year as a regular timestamp (1–52). The monthly average is defined as the mean of the parameter values for each month of the year over the years, from January to December (12 bins). Inter-annual average is the mean of the parameter values for each year, from 2001 to 2019 (19 bins). Average by seasons is the mean of parameters for the four quarters (March–May for spring, June–August for summer, September–November for autumn, and December to February of the following year for winter). For each bin, the standard error can be calculated as the standard deviation of the values as . Linear regressions and their associated statistics (slope, standard error of the estimated slope, p-value, correlation coefficient, ) were performed using the linregress functions from the Python library scipy.stats (Virtanen et al., 2020). The identification of clusters was done with the functions from the Python library (sklearn.cluster from KMeans, Pedregosa et al., 2011; https://scikit-learn.org/stable/modules/clustering.html). Ruptures in time series were investigated using the Python library ruptures (Truong et al., 2020; https://pypi.org/project/ruptures/). t test were calculated with the t functions from scipy.stats.
2.5 Machine learning: a random forest regression
To assess the weight of various contributors to the MLD dynamics, and identify which processes dominate, we perform a Random Forest Regression (RFR, Pedregosa et al., 2011), a supervised Machine Learning (ML) algorithm based on decision trees, that performs pattern recognition for classification/regression tasks. It starts by generating a set of binary decision trees with a random selection of variables. This collection of trees (the ‘forest’) is then used to evaluate a part (the ‘training set’) of our data-set of interest. It then uses ‘consensus’ among single decisions to assign a specific observation to a category (classification) or to predict a value (regression). By generating multiple training sets, the method can maximize signal and minimize the impact of noise in the data. In the context of this study, it can be considered an alternative, more flexible approach to nonlinear multiple regression. This method allows to obtain a score to input features (i.e., the predictors, or drivers) and their importance, that we want to exploit to identify how dominant they are into the projection, based on how useful they are to predict a chosen variable (i.e., here the MLD).
To modelize the MLD at the site, we select input variables that are nearly-independent from the in-situ observations to be able to apply the forecasting tool to projections. We apply the method to the weekly observations of MLD, using predictors estimated with some bulk variables (e.g., from ERA5): wind direction, wind stress, buoyancy fluxes, sea surface temperature, sea surface salinity outside the gulf, net precipitation rates, and the week of the year. To correlate consistently the observations to the forcings, the latter are averaged on the interval period between each MC cast (for example, forcings at MC466 are the average between MC465 and MC466, i.e., between the 5th (4th+1) and 10 January). Their importance in the fitting is then determined as the Gini importance in % (Breiman, 2001). We perform various trainings by splitting the time series by decade (I: 2001–2009; II: 2010–2019), and seasons (March–May for spring, June–August for summer, September–November for autumn, and December–February of the following year for winter).
Training is realized on 80% of the data available by subset, the 20% remaining being used for the validation. We use weekly estimates, and regressions are performed from 86 to 112 data points (see Table 4), depending on the MLD observations available (e.g., an average case of 4 weeks × 3 months × 9 years = 108 points). Each training variable is normalized to range its minimum and maximum from 0 to 1 (or −1 to 1 for signed quantities). Performance of the training is determined by comparing the MLD estimates to the monthly climatological values (i.e., the monthly atlas we could refer to if we did not have in-situ observations). Calculations are achieved through the RandomForestRegressor function from the module sklearn.ensemble (https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestRegressor.html).
3 RESULTS
Results are presented in three parts. The first part is dedicated to describing the ocean seasonal climatology at the LTER–MC station: the difference between the coastal site and the offshore area, the seasonal hydrology from the temperature and salinity profiles, and the seasonal budgets and environmental context of the GoN. The second part presents the inter-annual variability between 2001 and 2019: a general overview of the specific periods that impacted the heat and freshwater contents, the analysis of the inter-annual cycles at the LTER–MC station (trends, modulations, and decadal variations), and the impact on the inter-annual series of the MLD. Finally, the third part is focused on the inter-annual variability of the winter season: we propose the hypothesis that a regime shift occurred in winter after the transition 2009–2010, and we will investigate the different MLD's drivers between the decades 2001–2009 and 2010–2019 with the help of a Random Forest Regression.
3.1 Ocean climatology of the LTER-MC station
3.1.1 Coastal vs. open area: difference in the surface salinity between the Gulf of Naples and the open Tyrrhenian Sea
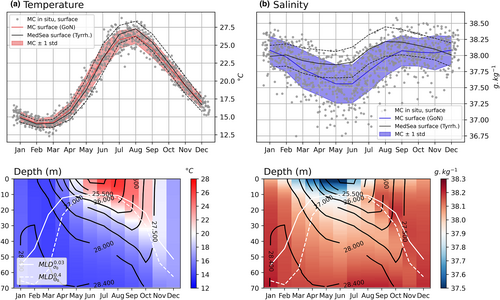
To introduce the time series analyses, we start characterizing the coastal and offshore water properties by comparing the difference between the seasonal cycle of surface temperature and salinity obtained from the observations in the GoN from 2001 to 2019, and the MS data reanalysis product, extracted in the Tyrrhenian Sea during the same period, that provides the open ocean context (see the two locations in Figure 1). Seasonality of the sea surface temperature is comparable (Figure 2, top left), though with around 1 °C difference in summer, but there is a difference in the cycle of surface salinity in amplitude and phase (Figure 2, top right). As it can be expected, coastal waters are generally fresher than the offshore, from around 0.15 to 0.35 g/kg. For salinity, the surface minimum outside and inside the Gulf occurs in May–June, while the offshore maximum is in August, and the coastal maximum is in September. Then the seasonal cycle at the coast shows some other partial maxima in December and January. The maximum precipitation shows its peak in November (Figure 3f), but the seasonal cycle displays important contributions from October to March, followed by the maximum of surface freshwater (or a minimum of salinity) in May–June, nearly 2 months later. From this overview, we can understand the coastal character of the site. It highlights the probable presence of horizontal advection mechanisms that could mitigate the offshore to inshore gradient, limit the exchanges of salt, and delay some freshwater imports. It is also worth mentioning that runoff and precipitation may display different time courses considering that, especially riverine runoff, reflect the hydrodynamics of the water catchment while, as for surface salinity minima and maxima, the vertical mixing occurring during winter months may blur the signal.
3.1.2 Seasonal hydrology in the GoN
Seasonal variations of salinity show a minimum of 37.4 g/kg occurring into the first 10 m of the surface layer from May to June (Figure 2, bottom). The maximum value of 38.2 g/kg is in January. A remarkable salty layer with values close to the maximum, between and 38.2 g/kg is visible from September to November, below 10 m depth and above the 20–50 m layer of relatively less salty water (38.0 g/kg). The thickness of this salty tongue increases in time following the deepening of the seasonal thermocline up to November, progressively filling the water-column, below the first 5 m, which display a less salty water of to 37.8 g/kg. In completement of the Figure 2, monthly averaged profiles can be consulted individually in Appendix S1 (Figure S3). Intrusions of salty water from 10 to 60 m create the conditions for salt-fingering below the MLD, as discussed by Kokoszka et al. (2021). Temperature shows a more classic seasonal cycle. A maximum of 26.4°C occurs in August (Figure 2, bottom). High values decrease from 26.0°C in July to 24.6°C in September. Potentially unstable water parcels appear during winter at the surface, from November to February, with the presence on the first 10 m of relatively cold water, around 0.05–0.25°C colder than the rest of the water-column. Stabilization of the water-column starts in March, after the annual minimum of 14.0°C, opening the summer period with a classic thermocline close to 20m deep during this season. Black contours Figure 2 (bottom) show the density estimates over the seasonal cycle. From January to April, density variation contours follow the estimation more closely (Figure 2, bottom, plain white lines), where the superscript defines the chosen threshold value to determine MLD (see Methods). From May to September, the MLD estimate falls within the 10 m depth limit, in line with the density field. From October to December, the visual fit would lead to a steeper variation than the two criteria above. When relying on the temperature-based estimate (Figure 2, bottom, dashed white lines), the effect of salty layers is not taken properly into account, and the seasonal cycle of the MLD estimated from temperature follows a steeper behaviour than the density-based one.
3.1.3 Seasonal budgets and environmental context of the GoN
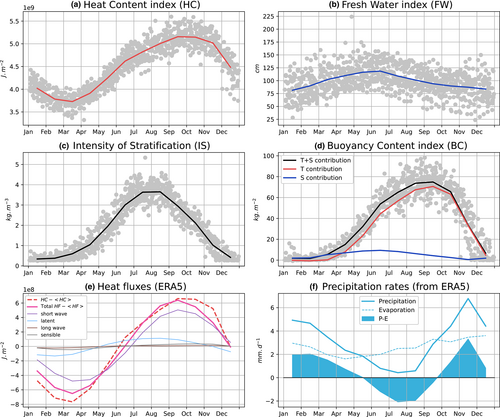
The mean seasonal cycle of HC has a minimum in March, , and a maximum in October at (Figure 3a,b). This cycle of the heat content is comparable to the ERA5 surface heat content from fluxes, once integrated in time. Figure 3e shows both HC and integrated HF cycles (centered on zero with the mean value being removed). The timing alignment is different, with the maximum of HC occurring in October, 1 month later than HF. Even if the net solar radiation dominates the fluxes, delay with the in-situ (GoN) estimation clearly suggests there are other contributors to the budget of the water-column. In terms of freshwater content, to reach the minimum of salinity in June, which is also the maximum deviation from a chosen reference value of (Figure 3b), a FW addition of nearly 112 cm would be needed, and these values are 85 and 80 cm for December and January, respectively. The freshest value appears to be later than the maximum of atmospheric freshwater and river discharge, which occurs from February to April (Mariotti et al., 2002), and is illustrated by the seasonal cycle of precipitation at the LTER–MC station that displays the most important contributions between October and March (with the peak in November, Figure 3f). Such delay is mostly due to the progressive accumulation of fresh water during the spring stratified period, which accumulates FW and concentrates it in a shallower MLD. However, circulation may also contribute to an occasionally decrease in salinity through the horizontal advection of freshwater across the shelf via filaments (Iermano et al., 2012).
An indication of the whole column stability is given by IS the intensity of the stratification, whose seasonal cycle in Figure 3c presents a distribution centered on July–August. The minimum value is 0.06 kg/m3 in January, and the maximum of 3.32 and 3.38 kg/m3 is in July and August. Finally, we complete IS with the depth-integrated buoyancy anomaly to the bottom (BC), which takes the full water-column content into account. In Figure 3d, BC presents a different distribution compared to IS, by being centered on September–October, to become steeper in December. This descriptor allows to discern between changes driven by buoyancy fluxes and involving the whole water-column from processes occurring in different layers for internal mixing and lateral advection. This shows the difference between IS and BC from May to November, bringing into question the choice of the best index to use to describe the state of the stratification, i.e., either by considering the surface and the bottom boundaries only (IS), or by including the contributions of the internal layers (BC). In Figure 3d, BC is decomposed between temperature (red line) and salinity (blue line) to determine their relative weight. BC is mostly driven by the temperature gradient, which contributes to a maximum difference of 64.2 kg/m2 in September, while salinity reaches its maximum contribution in June–July around 8.17 kg/m2, representing a factor of nearly 8 in favor of the temperature. But during winter periods, this dominant situation can flip and make salinity increase its contribution by a factor of 2 with respect to temperature. The main consequence of the salt contribution to the density is a limitation of the MLD estimates based on the density threshold, as showed on the mean salinity profiles in Figure 2 (bottom), where is generally shallower than with the presence of a saltier deep layer. This situation refers to the commonly known case of the barrier layer (Kara et al., 2000), noticeably frequent in tropical areas (Vissa et al., 2013), where MLD is overestimated when using temperature only, due to the seasonal contribution of salt to the density. Here, in a coastal environment, such as the GoN, this effect should be due to the dispersal of the runoff and not to direct precipitations, as is the case in the open ocean.
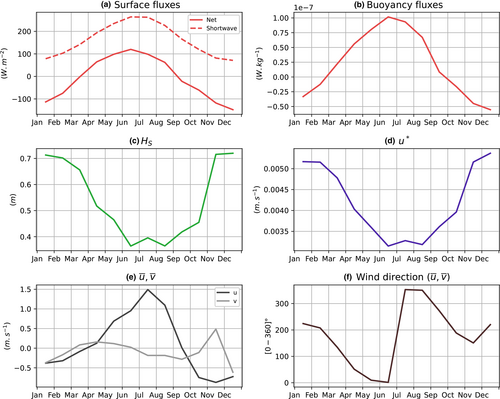
We complete the description of the environmental context of the GoN with the seasonal cycles of the physical parameters associated to the atmospheric forcings in Figure 4. Total surface fluxes vary from to 100 W/m2 with a maximum in June and a minimum in December–January, while shortwave fluxes are maximal in June and July (Figure 4a). Buoyancy fluxes reproduce this seasonal distribution and range in average from −0.25 × 107 to 1 × 10−7 W/kg, with a more regular increase from January to June and a steeper decrease from July to September (Figure 4b). Sea waves and wind stress co-vary seasonally (Figure 4c,d), the more intense seasons being winter (mean values of height of waves of 0.7 m and wind stress above ), while the quieter period is summer (mean values of height of waves of 0.4 m and wind stress close to ). Wind components (Figure 4e) have some interesting seasonal cycle, being westward in winter (close and above 0.5 m/s from October to February), and eastward in summer (above 1 m/s from June to August). The component has a different distribution, close to zero from February to June, southward in summer (close to 0.25 m/s from July to September) and winter (close to 0.5 m/s in December and January), and northward in November with speed close to 0.5 m/s. This results in winds oriented (Figure 4f) toward the East from May to August (angles close to 0° or 360°), toward the West from December to February (close to 200°), oriented toward the North quarter in March–April (1800°), and turning toward the South quarter in September, October, and November (mainly 360180°).
3.2 Inter-annual variability between 2001 and 2019
3.2.1 Unfold the temperature and salinity: some specific periods that impact the heat and freshwater contents
We calculate monthly anomalies to the mean seasonal cycle for T and S, in the layers of interest defined by the LTER–MC protocol (surface, 2 m, 5 m, then 10–60 m deep every 10 m). Results are presented in Figure 5. The inter-annual variability is clearly visible, and the succession of warm/cold and fresh/salty years is obvious to identify. This general overview indicates two types of anomalies for the temperature, from ±0.5 to ±1°C in a large part of the full water-column (e.g., warm in 2001, 2007, 2014, 2016, cold in 2004, 2006, 2012, or 2015), or intensified from ±1 to ±2°C in more local layers (e.g., surface and sub-surface in 2002–2005; closer to the bottom at the end of 2010, 2015 and 2018). Salinity is marked too, with moderate anomalies from ±0.05 to ±0.15 g/kg distributed in the water-column (e.g., salty in 2001–2003, 2006, 2012–2013, 2016–2017; fresh in 2004, 2009–2011, 2014–2015), or above ±0.2 g/kg in localized layers (e.g., in surface, salty in 2002–2003; fresh in 2004, 2010–2011, 2014). These anomalies are reflected in the water-column budgets anomalies of HC and FW (Figure 6). Minimum anomalies of HC are close to or below (e.g., in spring 2004–2006), with moderate ones from −0.5 × 108 to −1 × 108 J/m2 (e.g., in 2011–2013). Positive anomalies are close to or above (e.g., in spring 2001–2002, 2007, 2014), with moderate ones from 0.5 × 108 to 1 × 108 J/m2 (e.g., in 2008 or 2018). In Figure 6, the freshest years show anomaly values above 25 cm (e.g., in 2004, 2009–2011, 2014–2015). Driest periods are associated to negative values below −20 cm (e.g., in 2001, 2006, 2017).
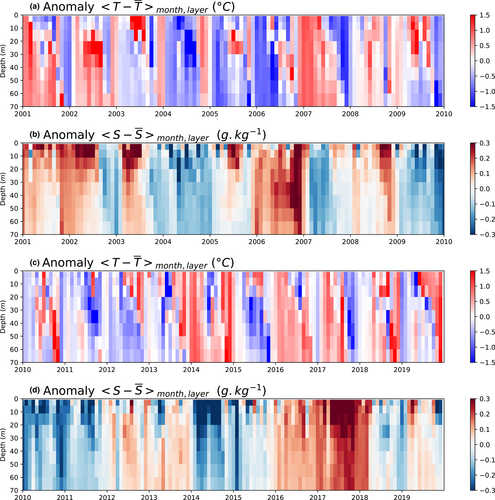

3.2.2 Inter-annual cycles: trends, modulations, and decadal variations
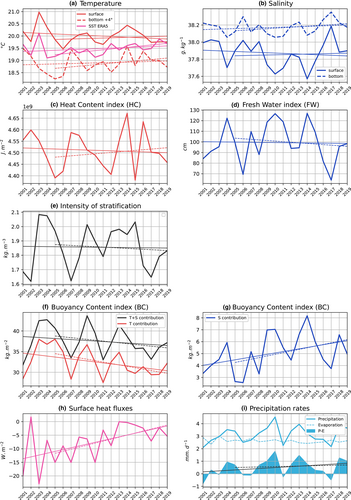
Thereafter we mention the 2001–2009 period as the decade I, and the 2010–2019 period as the decade II. In Figure 7, we show the inter-annual cycles of the quantities related to T and S, from in-situ observations and ERA5. Trends and modulations observed illustrate the complexity of the thermal and saline contributions in such areas. Linear trends are shown in Figure 7, for 2001–2019 ( solid lines) and 2005–2019 (dashed lines) periods. We warn the reader about the series, which must be long enough to be able to detect trends in a significant way. For some of the variables considered, 19 years may not be long enough. Nevertheless, for our investigation, we needed to systematically document the linear trends of each variable. Even if some are difficult to constrain due to the shorter-term oscillations (e.g., HC, FW), others have significant p-values (e.g., MLD, SST, HF, , ), as we will show thereafter. We chose the 2005–2019 period to avoid the influence of the 2003 heatwave in the trend calculation, this satisfies a sufficiently low level of auto-correlation (acc.) of the inter-annual series between 2005 and 2003 (, see Figure S4). The trends obtained during the 2001–2019 period are also presented, to avoid misleading the reader. Values are summarized in Table 2, and all the estimates are provided in the Appendix S1.
| Period (2005–2019) | Period (2001–2019) | |||||
|---|---|---|---|---|---|---|
| Linear trends/year | slope stde | p | Linear trends/year | slope stde | p | |
| LTER-MC | ||||||
| MLD | ±0.20 | .019 | ±0.14 | .05 | ||
| MLD winter | ±0.59 | .05 | ±0.38 | .004 | ||
| ±0.01 | .54 | ±0.015 | .32 | |||
| ±0.02 | .20 | ±0.016 | .62 | |||
| ±0.009 | .83 | −0.004 g/kg1 | ±0.007 | .58 | ||
| ±0.005 | .28 | ++0.003 g/kg1 | ±.003 | .42 | ||
| HC | .59 | .75 | ||||
| FW | ±1.17 | .65 | ±0.78 | .90 | ||
| ±0.18 | .28 | ±0.14 | .42 | |||
| ±0.16 | .06 | ±0.13 | .09 | |||
| ±0.09 | .18 | ±0.06 | .08 | |||
| IS | ±0.008 | .71 | ±0.006 | .92 | ||
| ERA5 | ||||||
| SST | ±0.009 | .004 | ±0.011 | .27 | ||
| P-E | ±0.041 | .73 | ±0.028 | .20 | ||
| BF | .002 | .004 | ||||
| .48 | .803 | |||||
| ±0.25 | .011 | +0.67 W/m2 | ±0.25 | .017 | ||
| ±0.25 | .87 | ±0.18 | .90 | |||
Regarding the surface temperature (Figure 7a), in-situ and satellite data indicate increasing trends of respectively and during the 2005–2019 period. Note that the heatwave event that occurred over all Western Europe during the summer 2003 (Olita et al., 2007) is visible here, and creates a negative slope (, 2001–2019) if it is taken into account to calculate the trend calculation for in-situ surface temperature. The bottom temperature follows a trend of (2005–2019) and exhibits a pseudo periodic modulation, too (from 3 to 5 years).
During 2005–2019, salinity data (Figure 7b) indicate trends of (surface) (bottom). We can see strong modulations in the surface salinity, with values in the range of 37.8–38.0 g/kg1 between 2001 and 2009, then in the range 37.6–37.8 g/kg between 2010 and 2015, and between 37.8 to 38.2 g/kg after 2015. These modulations make it hard to identify trends in the inter-annual time series (weak slope with non-significant p-value .59, Table 2). The same situation applies to surface temperature, for which modulations and the relative ‘shortness’ of the time series do not allow to constrain some significant trend (p-value .32). When considering the water-column budgets related to these quantities (FW and HC, respectively), the identification of trends is even more difficult, with weak slopes and non-significant p-values (.65 for FW, and .59 for HC, 2005–2019). But when looking at the contribution of salinity and temperature to BC, they both show clearer linear trends with more significant p-values (p-value of .18 for , and .06 for , 2005–2019). This could indicate that water-column budgets might not change (sensu of the weak trends detected for FW and HC), while stratification can increase or decrease ( and ).
In BC (Figure 7f), the total contribution of T and S (black line) shows a decreasing trend (, 2005–2019), with a periodic modulation having a delayed phase of 1–2 years compared to HC during decade I. Its thermal component (red line) follows the same modulation, and its decreasing trend is also visible (, 2005–2019). It is compensated in BC by the increasing trend of the saline component (, 2005–2019), in Figure 7g, which then shows a stronger contribution to the total BC during decade II. Our interpretation is the following: even when decreasing in intensity, the buoyancy is progressively reinforced in its saline component, stably ordered on the vertical dimension, i.e., relatively lighter (fresher) at the surface and relatively heavier (saltier) at the bottom. This could be the signature of the horizontal advection of different water parcels, whose rates of exchange between the coast and the offshore could lead the general trend observed in BC.
The long-term general variability observed for the inter-annual cycle of precipitations appears to impact the local content of salinity. P-E (Figure 7i) shows an increasing trend disrupted by groups of dry years, but establishing direct correspondence with salinity is complex. This is probably due to the mitigating effect of horizontal advection in the coastal area, importing both fresh runoffs from the coast, and salty parcels from the offshore, with various delays. Finally, the inter-annual cycle of the surface heat fluxes (, 2001–2019, and Figure 7h) reproduces the increasing trend well in the Mediterranean Sea, as shown by Criado-Aldeanueva et al. (2012). This macro driver is of interest as it describes the state of the large scale atmospheric forcings which applied to our regional area. Here we can describe its cycle in two periods, from low fluxes in decade I to higher fluxes in decade II. This descriptive framework will then lead to the inter-annual cycle of seasons, when these trends were stronger.
3.2.3 Impact on the mixed layer depth
In terms of proxy of the stratification, the mean inter-annual values of indicates a significant shallowing of during 2005–2019 (or during 2001–2019), the MLD being progressively confined toward the surface (Table 2). The inter-annual mean values of (Figure 8) identify 2007 as the year with the deepest mean MLD, nearly 32 m, while 2013, 2015 and 2019 are the years with the shallowest MLDs, with values lower than 19 m (Table 3). In addition, the cumulation of stratified weeks displays a wide range of values (Figure 8, grey line), with the shortest durations in 2002, 2003, 2007 and 2009 (from 26 to 29 weeks) and the longest ones in 2001, 2004–2005, 2011, 2013–2014, 2017 and 2019 (from 35 to 42 weeks, see Table 3 and Figure 8). Therefore, variations in stratification duration can go up to 3 months. The time series could be divided in groups of years displaying a long-term decadal trend interrupted by transition years, even if we have identified two main periods (I and II). Inside these two groups, various shorter periods can be identified. The 2001–2003 and 2004–2007 periods mark two deepening trends in the MLD, these are reflected in the two decreasing trends seen in the cumulated weeks. Then the period 2008–2011 shows a shallowing and an elongation of the cumulative, disrupted in 2012, and followed by a more constant period in 2013–2015 with a relatively shallow MLD (<20 m) and long stratified periods (from 35 to 38 weeks). The final part of the time series recalls in some part its beginning from 2001 to 2003, with a deepening in 2016–2018 followed by some shallowing in 2019. The change in the cumulated stratified weeks follows a period of 3 to 5 years. The time evolution of the mixed layer displays a significant inter-annual variability, with the initiation of the stratification fluctuating between March and April, and a progressive increase of its end in late autumn, with variations in the cumulated stratified weeks up to 3 months. The maximum duration occurred in 2011 over 42 weeks, which represents almost 80% of the year. In general, shallower mixed layer tend to last longer, while deeper ones tend to be shorter. The seasonal decomposition (Figure 8, bottom) allows us to identify the inter-annual series of the autumn seasons as the closest to the inter-annual cycle of the whole year. It is noteworthy that the inter-annual series of the spring seasons tend to present a moderate trend of deepening, with values below 15 m in 2003–2008, slightly shifting above 15 m during decade II. Winter is the season when the inter-annual trend and shift between decades is the most visible, during 2005–2019 (or during 2001–2019). During decade I, the water-column can be qualified of ‘fully mixed’ in winter () while the situation is rarer during decade II ().
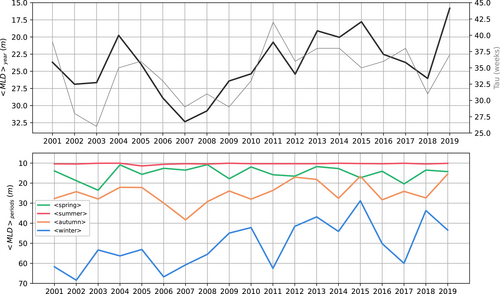
| Year | Start (weeks) | End (weeks) | (weeks) | |
|---|---|---|---|---|
| 2001 | 23.7 | 6 | 44 | 39 |
| 2002 | 26.9 | 15 | 42 | 28 |
| 2003 | 26.6 | 17 | 42 | 26 |
| 2004 | 19.8 | 13 | 47 | 35 |
| 2005 | 23.9 | 11 | 46 | 36 |
| 2006 | 28.9 | 12 | 44 | 33 |
| 2007 | 32.3 | 13 | 41 | 29 |
| 2008 | 30.8 | 12 | 42 | 31 |
| 2009 | 26.4 | 14 | 42 | 29 |
| 2010 | 25.4 | 9 | 41 | 33 |
| 2011 | 20.8 | 6 | 47 | 42 |
| 2012 | 25.4 | 12 | 47 | 36 |
| 2013 | 19.1 | 10 | 47 | 38 |
| 2014 | 20.0 | 8 | 45 | 38 |
| 2015 | 17.8 | 11 | 45 | 35 |
| 2016 | 22.5 | 10 | 45 | 36 |
| 2017 | 23.7 | 7 | 44 | 38 |
| 2018 | 26.0 | 14 | 44 | 31 |
| 2019 | 15.8 | 7 | 43 | 37 |
3.3 Inter-annual variability of the winter season
We identified the main drivers of the seasonal cycles, and the inter-annual modulations of the external forcing, such as the rain and the surface heat fluxes, with their impact on the in-situ budgets of heat content and freshwater. We investigate here the consequences on the MLD itself. Having identified winter as displaying a strong signal (, 2001–2019), we focus on the inter-annual variability of the drivers during that season. We introduce estimates of the regional forcings, calculated from the bulk variables extracted from the ERA5 data set (see Methods). To provide insights between mechanical and thermodynamical contributions to the deepening of the MLD, we use the fields of wind and surface heat fluxes to infer the wind friction () and the buoyancy fluxes (BF) at the sea surface. The variability of the wind intensity is informative of the local vertical mixing processes, but here we also investigate the variability of the wind direction since the boundary effect due to the geographic embayment of the LTER-MC station could have an influence on the accumulation/export of fresh/salty water parcels. On top of these quantities, we describe the time series of the climatic indices of the NAO and WEMO (see Methods) as a proxy of the atmospheric context of the neighbouring basins, which possibly influence our regional area, since it was shown to have a decadal impact on the northern part of the Mediterranean area (Bonifacio et al., 2019).
All selected variables are presented in Figure 9 (the time series for all seasons can be consulted in the Figure S2). Indices in Figure 9 reveal a shift to the Atlantic westerlies influence (i.e., positive NAO and WEMO) after 2010 that is particularly visible during winter seasons, while the WEMO index was quasi always negative during the decade I (i.e., steady dominant Mediterranean easterlies). To confirm that there is a significant rupture in the time series between the two decades, t test are performed on separated segments of the inter-annual winter series. Separation between decades is confirmed, with the best results obtained when comparing the segments (2001–2009) and (2010–2018). We obtain low p-values of .008 for MLD, .038 for (difference of surface salinity between the GoN and the offshore), .027 for , .064 for NAO, .004 for WeMO, and less significant p-values of .206 and .234 for BF and the wind direction. This reinforces the situations we depicted previously about the two decadal periods, I and II, inside which the interplay and dominance between drivers could have been different.
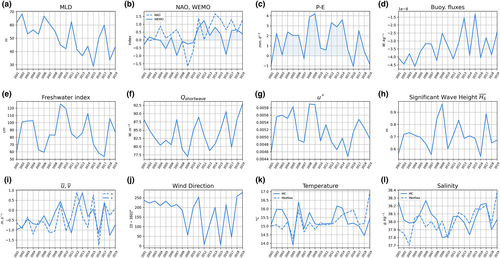
3.3.1 The hypothesis of a regime shift in winter after the transition of 2009–2010
The seasonal decomposition reveals an interesting variability, with a possible winter shift after the transition of 2009–2010, as NAO and WEMO indices suggest a regime shift that happened in winter after the years 2009–2010 (Figure 9b), suggesting an Atlantic influence over the Mediterranean area, possibly observable at the LTER-MC point. The study of D. Smith et al. (2014) illustrates the winter condition of the NAO index well in 2009–2010, the index describes how the direction and speed of the prevailing winds are controlled. The winter of 2009/2010 is a remarkable recent negative case: the winter mean meridional gradient of sea-level pressure was of opposite sign to the usual climatological gradient, corresponding to winter mean easterly flow from the Central–Europe/Mediterranean-basin and across the Atlantic (their Figure 1). The authors propose a useful review of the potential drivers of the NAO (their Figure 2), and point to the difficulty of defining the dominant one. The study of Fereday et al. (2012) investigated the case, and suggested an influence of El Nino that would have led to a sudden stratospheric warming, producing a stronger sea level pressure signal. The authors list other possible drivers of the European winter climate, including Atlantic SST, volcanic eruptions, snow cover, and solar forcing. In particular, the anomalous snow cover and solar minimum in 2009/10 may have contributed to the conditions observed. More recently, the study of Börgel et al. (2020) linked the NAO variability to the Atlantic Multi-decadal Oscillation, which induces some changes in its influence on regional climate variables.
At this point in our study, we do not aim to disentangle between the influence of NAO and WEMO in the Tyrrhenian coastal area, and we will consider both indexes, as the authors pointed their importance in the Mediterranean area, not only in terms of precipitation (Lopez-Bustins & Lemus-Canovas, 2019; Tsanis & Tapoglou, 2019), but also with changes of storm tracks, from the Euro-Atlantic area over the Southeast Europe (Caian et al., 2021). NAO could be used to explore the potential penetration of the North Atlantic depressions into the Mediterranean, although the effect over the Italian Peninsula is not well understood Sánchez and Aragão (2021) (conference paper).
The regime shift between East-Mediterranean and West-Atlantic is visible in the wind trades (Figure 9j), showing the appearance of winds toward the coast (below 150°, so orientated toward East to Northwest), marking a difference with the dominance of the wind toward the offshore during the decade I. In the wind friction (Figure 9g), the inter-annual series is marked by diminishing energy with friction passing from around (decade I), to around (decade II). We showed that the mixed layer can be limited in winter by the surface salty content, and this could be amplified by the increase in salt visible in Figure 9l during decade II. Interestingly, during this period, this signal seems to align with the surface offshore salinity. This could be an indicator of facilitated exchange with the open Tyrrhenian area in the horizontal import/export of inshore/offshore parcels. The increase in the convective BF is visible too (Figure 9d), going from low values of −3 × 108 to −4 × 108 W/kg before the mid 2010s, to larger values after.
3.3.2 Investigation of the mixed layer depth's drivers
3.3.2.1 Two different regimes in winter in functions of the wind and the buoyancy fluxes
The winter trends revealed a remarkable relationship between the MLD and the wind stress during the two decades. In Figure 10, a linear trend is visible between the average and during decade II (p-value of .007)
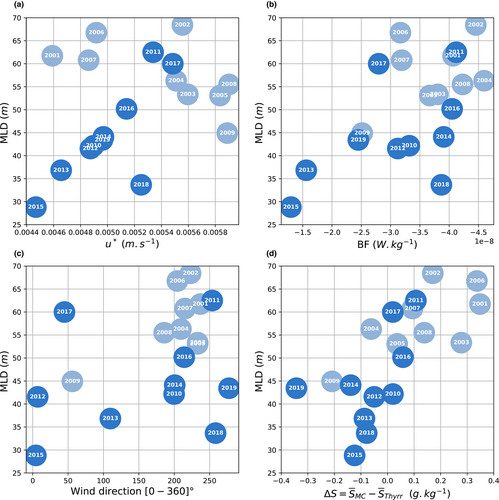
. Decade II shows a linear control, with low/high wind stress associated to a shallow/deep MLD regime, not visible during the decade I (p-value of .074). Interestingly, decade I indicates a cluster of deep MLD (>50 m, scenario of a deep MLD ) associated with intense low BF (), while decade II suggest a more linear distribution (scenario of a shallow MLD). In terms of wind direction, decade I indicates the dominant directions centred on around 220° (blowing toward the South–West quarter, i.e., in direction of the offshore), while decade II shows more variance, with directions spreading widely Northward direction (i.e., towards the coast). When looking at the inshore–offshore gradient of salinity at the surface, deep values of MLD are associated with the largest and positive differences between the GoN and the Tyrrhenian area (i.e., the GoN relatively saltier), while the decade II shows an increasing coupling with the open area, with differences decreasing to zero, or being negative (i.e., GoN relatively fresher). Due to the presence of mesoscale features all year long, we hypothesize that a coupled configuration would be favorable to express the influence of such structures inside the GoN by redistributing fresh/salty parcels during decade II.
3.3.2.2 Relative contributions of the selected drivers to the MLD's modelization
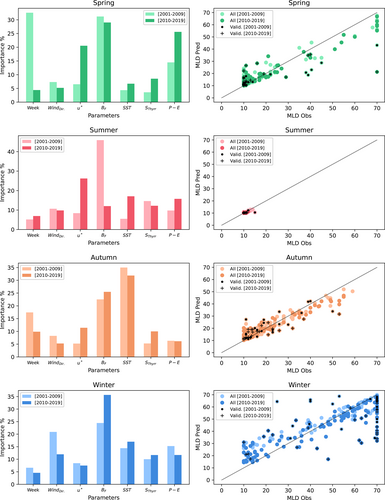
To go further and extend this analysis to the other seasons when the trends of the MLD are less marked (i.e., spring and autumn), we perform a random forest regression to assess the individual weights of the various contributors to the MLD (see Methods). We aim to modelize the in-situ MLD in the function of independent external variables (i.e., external data-set such as ERA5 provided by Copernicus). For this, we hypothesize that the large-scale atmospheric conditions (sensu climate indices NAO or WEMO) could have led to different dynamical regimes, i.e., thermodynamical (e.g., convective fluxes) and mechanical (e.g., wind stress) forcing could have varied in dominance and timing. To distinguish between possible cases, the regression tree has been trained by subsets, splitting the time series by seasons and decades, trying to reproduce the observations of the MLD with the help of predictors. The importance of the predictors is shown in Figure 11, left, to the side of scatter plots of the MLD predicted (Figure 11, right). Given the strong vertical gradient of density in summer between the surface and the rest of the water-column, the MLD estimates in this period tend to be close to any chosen reference depth, its range of variation is therefore artificially limited, and the summer variability is difficult to interpret. Taking into account these limitations, we did not interpret the results of the regression during this season. Performance values are presented in Table. 4: in general, the regression performed well, and better for a decade I (correlation of .89) than decade II (.75). We show that the regression could be useful to propose an estimate of the MLD when in-situ data of the water-column are not available, and only external variables are. In this case, the only estimate available from the observations would be a climatological value obtained from the weekly time series (e.g., atlas value). We show here that, in general, the mean error between prediction and validation data is lower than if using an atlas value when compared to observations (i.e., using the 2001–2019 monthly averages of MLD): estimates are improved when predictions are used.
| (2001–2009) | |||||
|---|---|---|---|---|---|
| All | Spring | Summer | Autumn | Winter | |
| Data (N) | 468 | 117 | 117 | 108 | 126 |
| Training (N) | 374 | 93 | 93 | 86 | 100 |
| Validation (N) | 94 | 24 | 24 | 22 | 26 |
| 27.0 | 18.5 | 10.5 | 22.2 | 55.4 | |
| 23.3 | 16.8 | 10.3 | 22.8 | 51.2 | |
| 26.8 | 15.5 | 10.4 | 22.6 | 58.4 | |
| 7.91 | 6.80 | 0.57 | 6.40 | 16.4 | |
| 5.93 | 5.50 | 0.41 | 5.00 | 13.8 | |
| 73.8 | 78.1 | 96.65 | 73.9 | 57.2 | |
| Linear regression vs. | |||||
| .79 | .89 | .27 | .63 | .09 | |
| p | .0 | .0 | .00978 | .00001 | .12051 |
| Corr. coef. | .89 | .94 | .52 | .80 | .31 |
| (2010–2019) | |||||
|---|---|---|---|---|---|
| All | Spring | Summer | Autumn | Winter | |
| Data (N) | 520 | 130 | 130 | 120 | 140 |
| Training (N) | 416 | 104 | 104 | 96 | 112 |
| Validation (N) | 104 | 26 | 26 | 24 | 28 |
| 23.3 | 16.2 | 10.2 | 18.0 | 49.2 | |
| 25.9 | 17.2 | 10.4 | 20.0 | 49.4 | |
| 24.0 | 16.2 | 10.2 | 17.2 | 39.6 | |
| 9.55 | 5.99 | 0.46 | 6.11 | 19.0 | |
| 8.04 | 5.44 | 0.29 | 4.35 | 17.8 | |
| 59.3 | 69.9 | 97.3 | 78.8 | 52.7 | |
| Linear regression vs. | |||||
| .56 | .33 | .12 | .70 | .32 | |
| p | .0 | .00186 | .07647 | .0 | .00174 |
| Corr. coef. | .75 | .58 | .35 | .83 | .56 |
When looking at individual seasons by decades, training assimilation of winter, I was more difficult, with less performing fit well (p-value of .12) than for winter II (significant p-value of .00174). In spring and autumn, a better performance is obtained in predicting the MLD, and for both decades, the errors are reduced when using the prediction instead of the atlas. Without considering the limitations, we show the good performance of the method. Even if the results in winter have to be carefully considered, we briefly describe them here for the sake of completeness. During the decade I, wind direction (more than 20%) and BF (around 25%) are dominant factors, while during decade II, BF dominates (more than 30%). BF is more stabilizing during this decade, with the general tendency of heat increase, and, as suggested before, this reinforces the hypothesis that wind stress has a greater role in mixing the surface layer. To resume: the situation of deep MLD (decade I) could be set by the consistent wind direction toward the offshore (dilution of the coastal fresh runoffs), and strong convective BF, reinforced secondarily by the intermittent wind events. Then the situation of a shallow MLD (decade II) could result from a change in the wind direction retaining the fresh water parcels close to the coast, with a more stable BF, and a wind stress controlling linearly the deepening of the MLD, given the more stable configuration. This situation could be repeated in spring during decade II as P-E changes from 15% to 25%, and the wind stress from 5% to 20%. This interpretation could be applied to autumn, too, with more importance given to the SST (more than 30%), whose increase could matter to the shallowing tendency of the MLD. This could set the stable configuration, against which the wind stress (importance increasing from 5 to 10% between decade I and II) could express its linear control of the deepening, as proposed for the winter configuration.
4 DISCUSSION
Our detailed analysis of the 2001–2019 time series of temperature and salinity at the LTER-MC station allowed us to extend and complete the former study by Ribera d'Alcala et al. (2004) by characterizing the relative importance of the main drivers of the water-column dynamics for this specific site over the two decades. This creates an appropriate framework to formulate hypotheses on the impact of predicted climate changes on the area and to depict possible scenarios with which plankton communities should scope in the near future. The link between plankton dynamics at the site and the water-column structure is the subject of an ongoing analysis which necessitated the work presented here.
4.1 Overview of this coastal area: classic in temperature, specific in salinity, both subjected to seasonal and inter-annual trends
The climatological pattern at the site displays a classic seasonal cycle for temperature (minimum in February–March, maximum in July–August), whose inter-annual trend follows the warming trend inferred from the satellite observations on the temperature surface, locally or over the whole Mediterranean basin since the mid 2010s (Iona et al., 2018). This increasing trend is weak and overlaps with a modulation of multi-annual periods, from 3 to 5 years, discussed thereafter. We show that warming impacted the full water-column in such a shallow area, where variability is dominated in amplitudes by some oscillating multi-annual modulations following a weak linear trend. This suggests the need for longer consistent monitoring to identify more significant linear trends.
Salinity also plays an important role in the water-column stability via the establishment of the surface freshwater layer in spring and of the salty water layer at mid-depth in September–November. This saltier water is an intrusion of offshore water, marking a specific dependency of this coastal site to the regional ocean circulation. Because of this intrusion, the water-column is divided in three layers, with salinity maximum and intermediate temperature, which promotes double diffusion with the surface and the bottom layer, as shown in Kokoszka et al. (2021) that highlighted the presence and persistence of density staircases below the MLD from late-summer to early-winter. This could have an effect on the MLD itself, as it stabilizes the surface layer, and could drive the prolongation of the stratified period longer in the season, as discussed thereafter. The maximum of freshwater input occurs before the salinity minimum since it is masked by the vertical mixing in later winter. Moreover, this creates the condition of a barrier layer (Kara et al., 2000; Vissa et al., 2013), leading to an overestimation of the MLD if inferred from temperature profiles instead of density, that includes this haline contribution. This salty water type results from the summer evaporation occurring in the Tyrrhenian sea or in the outer part of the Gulf, since the surface layer at the site is, for most of the time, fresher than the water underneath, because of the inputs from the coast, or because of fresh water advected from the close Sarno river (Cianelli et al., 2012, 2017), or from the neighboring Gulf of Gaeta (Iermano et al., 2012). Considering the surface, the preliminary comparison with the offshore area revealed the importance of fresh runoffs effects on the salinity cycle as observed at the LTER-MC point in the GoN, having its minimum in May–June 2 months later than the last winter inputs of fresh water occurring in February–March. This is also evidenced through the salinity values, which are generally lower than the typical values of the Tyrrhenian sea (Napolitano et al., 2014).
This reveals the influence of fresh water content on the coastal character of the site, spanning over a longer time than the regional inputs, and suggests the presence of horizontal advection mechanisms that mitigate the offshore/inshore salty exchanges (Iermano et al., 2012, Cianelli et al., 2015). From this simple climatological cycle, we assume a complex interplay between vertical processes and variable horizontal inputs, since the stratification at the site does not simply result from the strict local atmospheric forcing, heat and momentum fluxes, and precipitation, but is significantly impacted by land inputs on one hand and coupling with larger scale circulation on the other.
4.2 What do we learn from the trends we can observe at the coastal area?
The inter-annual cycle of the surface heat fluxes (Figure 7h) reproduces the decadal variability observed in the Mediterranean Sea well, with the increasing trend initiated from the mid 2010's shown in Criado-Aldeanueva et al. (2012). We can identify two cycles within its cycle, from low fluxes between 2001–2009, to higher fluxes between 2010–2019. In terms of atmospheric context, two opposite trends are visible in the surface fluxes, during a quasi bi-decadal period, while NAO and WEMO indices suggest a regime shift in the winter seasons after the years 2009–2010 (Bonifacio et al., 2019; Fereday et al., 2012; Smith et al., 2014). This could have led to a different interplay between wind and convective forcings, that we will discuss thereafter. We show that, even while being in a shallow coastal area, the site is not only influenced by local land inputs (fresh runoffs), but also by basin-scale drivers whose differentiation is rendered complex to establish by the combination of their multi-decadal and decadal variabilities, as shown and discussed by Parker et al. (2007), or more recently, in the works of Börgel et al. (2020), Zhang, Chen, Chen, Ma, & Teshome (2020); Zhang, Villarini, Scoccimarro, & Napolitano (2020) on the North Atlantic multidecadal variability in the mid-high latitude. In our study, we pave the way towards a better understanding of such interactions in the Tyrrhenian and Mediterranean Sea (Caian et al., 2021; Lopez-Bustins & Lemus-Canovas, 2019; Tsanis & Tapoglou, 2019), which could impact the coastal marine ecosystems services of the GoN.
More locally, we showed that the main driver of the fresh water budget is precipitation, directly and indirectly, which has significantly more impact than evaporation. It implies that long term changes are also possibly impacted by the effects of climate change on the surrounding territories, which include regions with important winter snow accumulations (note the proximity of Mount Vesuvius, in the northern part of the GoN, and the Monti Lattari in its south–eastern part, these mountain systems having altitudes higher than 1200 m). However, it is not only the local precipitation, i.e., that those directly fall in the Gulf, but also those conveyed to the GoN via the catchment area land side of the Gulf that contribute. Note that the river runoffs contribution (see the dedicated analysis into Appendix S1) were not accounted for, despite their likely importance over this coastal area: The Sarno river runoff into the Gulf of Naples is about 13 m3/s, while the Volturno river runoff into the Gulf of Gaeta is about 82 m3/s (Albanese et al., 2012). Further stratification enhancement derives from the contrast between a fresher surface layer and saltier layer underneath, which is very seldom interrupted by events of flushing by offshore waters and which reinforces the prolongation of the stratified period and the tendency toward a shallower MLD over the years. In a context of rising air and sea temperatures, and of intensifying extreme events such as storms, floods, and even, recently, Mediterranean hurricanes, the fresh water influence becomes a primer in such regional area surrounded by land and mountains (Koseki et al., 2020; Volosciuk et al., 2016; Zhang, Villarini, et al., 2020).
The system being fresher and more stratified, it raises the question of its connectivity to the offshore. Interestingly, the seasonal decomposition and comparison with the neighbouring Tyrrhenian Sea during winter suggested an enhanced coupling between offshore and inshore during the decade 2010–2019. It remains to determine if such coupling was facilitated by a shallower winter MLD (i.e., more stratified situations) that promoted horizontal exchanges between the gulf and the open area. The mesoscale contribution, through water parcels, mixing, and advection, remains to be investigated too. Its seasonality may be different from the seasonality of external drivers, as vortices structures are present all year long (Bonaduce et al., 2021; Fernandez et al., 2005), and submesoscale flows are expected to be much stronger in winter than in summer (Callies et al., 2015). The role of submesoscale (e.g., the formation of filaments), depends also on the runoff input of high potential vorticity (maximal in spring and early summer), and in general, from anomalies in the stratification. An enhanced coupling between the inner/outer areas during the decade 2010–2019 could have then promoted trade-offs driven by such structures, whose role on the redistribution of the water parcels (fresh or salty) inside the Gulf remains to be determined.
4.3 MLD: a proxy of the stratification resulting from interplaying processes
The MLD, taken as a proxy of the stratification, evolved over the years (Figure 8), while the macro indexes (intensity of the stratification, and buoyancy anomaly content, Figure 7e,f) neither reflected the same evolution. Even if marked by the periodic modulations discussed before, the inter-annual average of the MLD shows a remarkable shallowing trend (Table 2). The MLD is progressively confined towards the surface, and there is also an increasing trend of the cumulated stratified weeks during the whole 2001–2019 period (from shortest between 26 to 29 weeks, to longest from 35 to 42 weeks). This long-term variation is interrupted by transition years, and the change in the cumulative shows the same modulations than those observed in the thermal and saline drivers.
When decomposing by seasons, we identify that the inter-annual series of the autumn seasons is the closest to shallowing inter-annual series of the whole year, while a moderate trend of deepening is visible in spring with values above 15 m deep (decade II). This might be due to the salinity that contributes 50% more than temperature to the buoyancy content, in general, from January to April (e.g., with the presence of cold and salty water parcels in the water-column, remaining from the winter period). Winter is the season when the inter-annual trend is the most visible, with a remarkable shift between the 2001–2009 and 2010–2019 periods: the water-column was more frequently ‘fully mixed’ during the decade I, and less frequently during decade II. As shown by Zingone et al. (2010), the winter period is of importance for the physical and biological marine ecosystem of the Gulf of Naples, as it sometimes reproduces (prolongates) the late-summer conditions (relatively rich in nutrients because of episodic inputs from land), and primes the primary production for the next spring.
We propose a speculative scheme about the fresh runoff inter-playing with the wind stress at the surface layer, from the end of summer to winter. We present our hypothesis about the mixed layer control: some freshwater is accumulated and transported at the surface of the Gulf, then is disrupted by the wind. Under easterlies conditions (e.g., the dominant wind regime suggested during 2001–2009), the river fresh water output could be exported offshore and diluted within the ambient salty water, leading to the classic situation of a mixed layer extended to the bottom, controlled primarily by both destabilizing convection and wind mechanical mixing (e.g., the decade I). Switching the wind regime to dominant westerlies (e.g., as suggested in 2010–2019), and taking into account that a continuous river discharge occurs at the coastal boundary, the situation could lead to an accumulation of fresh water at the coast, as it has been suggested by Cianelli et al. (2017). This amount of water could inhibit the convective processes and limit the mixed layer to shallower depths, compared to the other case involving easterlies. In cases where the surface heat fluxes would be less destabilizing (e.g., decade II), the mixed layer control could be mainly driven by the wind, as suggested by our inter-annual analysis of the winter season. In this context, the timing of intense wind events could be a primer, by disrupting intermittently the stably stratified state and mixing the water-column. This could explain the elongation of the stratified period, as observed during the 2010–2019 autumnal periods, that could have resulted from the conjunction of more westerlies winds, late storm events, and fresh water discharge into the system after precipitations.
4.4 The GoN as a monitoring area of physical and biological changes
When considering the Gulf of Naples in full, our study highlights the complexity of the ocean circulation that influences the coastal observations, as pointed out recently in the work of de Ruggiero et al. (2020) that assessed the dynamics of the area during a specific year (2016). Between its inner areas, the GoN is subject to various connectivities which remain to be identified precisely to quantify the impact on the dynamic and variability of the biological communities. For this, a Lagrangian study should be done by following chosen particles inputs (e.g., nutrients and pollutants discharge from the Sarno river, coastal runoffs from particular drains, or oligotrophic offshore waters) using ocean drifters and trajectories in the numerical model. This would highlight the coupling between physics and biology when the coastal system experiences long-term trends, inter-annual modulations, and extreme events: What are the biological responses to such stresses (or opportunities) on the ecosystem communities?
In the context of climate change, we expect that the Mediterranean basin would go through an increase in fresh inputs (Alpert et al., 2013), with heat waves occurring intermittently (Darmaraki et al., 2019; Holbrook et al., 2020). This would cause an increase of evaporation, leading to an increase in salinity (Skliris et al., 2018) with a parallel increase in density, very weakly compensated by the increase in temperature. Accurate knowledge of the horizontal fields of salinity and wind stress are required to correctly determine the onset and breakdown of the stratification (Ruiz-Castillo et al., 2019). The local state of the surface layers is of importance here, and also the interplay with remote factor such as basins scale climate indices (i.e., NAO and WEMO), as the timing and intensity of wind events have been shown to be controlled by larger scale features. In this case, a regime shift could impact the variability of important variables such as the wind, and, consequently, its directional forcing on the coastal system. Moreover, more stratification leads to inhibit the exchanges between the internal layers of the water-column and the atmosphere, and promotes some internal wave activity (Woodson, 2018), changing the way nearshore ecosystems are exposed to deep offshore waters. The present study of the long-term time series, from CTD observations obtained with a consistent effort—but however relatively simple, shows the importance, as pointed recently by Bonifacio et al. (2019), to accumulate and build regional climate indexes. It is nevertheless important to underline that our study focused on a single coastal fixed station, and other confronts with comparable sites in the western Mediterranean Sea region should be led through inter-comparisons studies. Our study proposes a step forward to the constitution of some index and atlas for future studies, that could strengthen the predictability of the marine coastal ecosystems with the joint contributions of numerical simulations, recent modelization techniques such as machine learning, and comparisons to in-situ observations.
ACKNOWLEDGMENTS
Data sets for this research are available presently on request, as the data paper is in preparation. We would like to thank the LTER-MC team that includes, besides the main authors: D. d'Alelio, C. Balestra, M. Cannavacciuolo, R. Casotti, I. Di Capua, F. Margiotta, M. G. Mazzocchi, M. Montresor, A. Passarelli, I. Percopo, M. Saggiomo, V. Saggiomo, D. Sarno, F. Tramontano, G. Zazo, and A. Zingone, all based at Stazione Zoologica Anton Dohrn of Naples. Special thanks must be given to A. Passarelli and the commandants and crews of the R/V Vettoria for all their dedicated work at sea. The research program LTER–MC is supported by the Stazione Zoologica Anton Dohrn.
Open Research
DATA AVAILABILITY STATEMENT
The ocean in-situ CTD data that support the findings of this study are available from the corresponding author, [F.K.], upon request, until it will be made available directly online. The external data that support this study are openly available: the Mediterranean MFC physical reanalysis is available at https://doi.org/10.25423/CMCC/MEDSEA_MULTIYEAR_PHY_006_004_E3R1, the ERA5 ECMWF reanalysis for the global climate and weather at https://doi.org/10.24381/cds.adbb2d47, the River discharge and related historical data from the European Flood Awareness System at https://doi.org/10.24381/cds.e3458969, the NAO index at https://www.cpc.ncep.noaa.gov/products/precip/CWlink/pna/nao.shtml, and the WEMO index at http://www.ub.edu/gc/wemo/.




