Volume 43, Issue 1 e13025

ORIGINAL ARTICLE

Open Access

Mathematical modeling of Bacillus cereus in Saengsik, a powdered ready-to-eat food and its application in quantitative microbial risk assessment

Daekeun Hwang,

Daekeun Hwang

Food Safety and Distribution Research Group, Korea Food Research Institute, Wanju, Republic of Korea

Department of Food Biotechnology, University of Science and Technology, Daejeon, Republic of Korea

Search for more papers by this author

Jin Hwa Park,

Jin Hwa Park

Food Safety and Distribution Research Group, Korea Food Research Institute, Wanju, Republic of Korea

Search for more papers by this author

Yohan Yoon,

Yohan Yoon

Department of Food and Nutrition, Sookmyung Women's University, Seoul, Republic of Korea

Search for more papers by this author

Sang-Do Ha,

Sang-Do Ha

orcid.org/0000-0002-6810-2092

Department of Food Science and Technology, Chung-Ang University, Anseong, Republic of Korea

Search for more papers by this author

Min Suk Rhee,

Min Suk Rhee

Department of Biotechnology, Korea University, Seoul, Republic of Korea

Search for more papers by this author

Minseon Koo,

Minseon Koo

Food Safety and Distribution Research Group, Korea Food Research Institute, Wanju, Republic of Korea

Department of Food Biotechnology, University of Science and Technology, Daejeon, Republic of Korea

Search for more papers by this author

Hyun Jung Kim,

Corresponding Author

Hyun Jung Kim

[email protected]

Food Safety and Distribution Research Group, Korea Food Research Institute, Wanju, Republic of Korea

Department of Food Biotechnology, University of Science and Technology, Daejeon, Republic of Korea

Correspondence

Hyun Jung Kim, Food Safety and Distribution Research Group, Korea Food Research Institute, Wanju, Jeollabuk-do 55365, Republic of Korea

Email: [email protected]

Search for more papers by this author

Daekeun Hwang,

Daekeun Hwang

Food Safety and Distribution Research Group, Korea Food Research Institute, Wanju, Republic of Korea

Department of Food Biotechnology, University of Science and Technology, Daejeon, Republic of Korea

Search for more papers by this author

Jin Hwa Park,

Jin Hwa Park

Food Safety and Distribution Research Group, Korea Food Research Institute, Wanju, Republic of Korea

Search for more papers by this author

Yohan Yoon,

Yohan Yoon

Department of Food and Nutrition, Sookmyung Women's University, Seoul, Republic of Korea

Search for more papers by this author

Sang-Do Ha,

Sang-Do Ha

orcid.org/0000-0002-6810-2092

Department of Food Science and Technology, Chung-Ang University, Anseong, Republic of Korea

Search for more papers by this author

Min Suk Rhee,

Min Suk Rhee

Department of Biotechnology, Korea University, Seoul, Republic of Korea

Search for more papers by this author

Minseon Koo,

Minseon Koo

Food Safety and Distribution Research Group, Korea Food Research Institute, Wanju, Republic of Korea

Department of Food Biotechnology, University of Science and Technology, Daejeon, Republic of Korea

Search for more papers by this author

Hyun Jung Kim,

Corresponding Author

Hyun Jung Kim

[email protected]

Food Safety and Distribution Research Group, Korea Food Research Institute, Wanju, Republic of Korea

Department of Food Biotechnology, University of Science and Technology, Daejeon, Republic of Korea

Correspondence

Hyun Jung Kim, Food Safety and Distribution Research Group, Korea Food Research Institute, Wanju, Jeollabuk-do 55365, Republic of Korea

Email: [email protected]

Search for more papers by this author

First published: 11 November 2022

https://doi.org/10.1111/jfs.13025

Funding information: Ministry of Food and Drug Safety, Grant/Award Number: 17162MFDS035

Share a link

Email
Wechat
Bluesky

Abstract

In this study, we developed a mathematical model to describe the fate of Bacillus cereus in Saengsik, a powdered ready-to-eat food with reduced moisture content, and to estimate the probability of B. cereus infection from Saengsik consumption, using quantitative microbial risk assessment (QMRA). The isothermal kinetic behavior of B. cereus was analyzed as a function of temperature (5–40°C). Bacterial cell counts were fitted to the Weibull model using GinaFit, and the obtained delta values (required time for the first decimal reduction) for each temperature were 128.3–17,124.1 hr and concave (ρ < 1) were observed under all experimental conditions. The obtained delta values were analyzed using the Davey model as a function of temperature, and the performance of the developed model of survival of B. cereus was appropriate based on the validation parameters (B_f, A_f, and RMSE) within the acceptable range. QMRA model was developed using data on the prevalence and concentration of B. cereus along with time and temperature along the retail-to-consumer steps. Using a baseline model with the currently available data, the probability of B. cereus infection was zero. These results provide useful information for the risk assessment and management of microbial risk in foods, especially those with very low-moisture content.

1 INTRODUCTION

Bacillus cereus is a Gram-positive spore-forming facultative anaerobic bacterium, with a size of 0.5 × 1.5 μm. It is widely distributed in nature and is a frequent contaminant of raw food materials such as vegetables, grains, and spices (Ray & Bhunia, 2013). B. cereus spores are resistant to physical and chemical conditions and, therefore, can survive during common food processing procedures, manufacturing, and cooking of food. If appropriate conditions are available, vegetative cells can grow vigorously and cause food spoilage and deterioration (Giaouris & Simões, 2018). B. cereus induces diarrhea-type or vomiting food poisoning, which are caused by enterotoxin or emetic toxin (cereulide), respectively. The latter toxin is a metabolite produced by growing bacteria (Ray & Bhunia, 2013).

With the increasing demand for mildly processed foods, B. cereus outbreaks have increased in Korea, as well as worldwide. Foodborne illness caused by B. cereus in Korea has been steadily occurring over the past decade (Ministry of Food and Drug Safety, 2020), and has been reported in many countries (Galié, García-Gutiérrez, Miguélez, Villar, & Lombó, 2018; Osimani, Aquilanti, & Clementi, 2018; Rouzeau-Szynalski, Stollewerk, Messelhäusser, & Ehling-Schulz, 2020). In 2018, B. cereus was involved in 98 reported outbreaks among the European Union members (EFSA and ECDC, 2019). Recent outbreaks have been also associated with this pathogen (Choi & Kim, 2020; Osimani et al., 2018), for example, 45 cases identified in an outbreak at an Australian restaurant (Thirkell, Sloan-Gardner, Kacmarek, & Polkinghorne, 2019). Various foods, such as pasta salad, spaghetti, tomato sauce, navy beans, re-fried beans, and water, acted as vehicles for transmission of B. cereus, resulting in hospitalizations and deaths (Choi & Kim, 2020). Low-moisture foods with low-water activity (a_w < 0.85) are considered less susceptible to microbial spoilage and the growth of foodborne pathogens (Sánchez-Maldonado, Lee, & Farber, 2018). However, long-term survival of pathogens in low-moisture foods has been reported for years, depending on storage conditions, such as temperature (Reiji, Masakado, Kenji, & Yutaka, 2005). In particular, B. cereus has been considered a concerning pathogen in low-moisture foods (Bourdichon et al., 2021).

Saengsik, a powdered ready-to-eat food with low-a_w, is a mixture of dried raw grains and other ingredients such as fruits, mushrooms, and seaweeds. It is typically manufactured by washing, drying, crushing, mixing, and packaging raw materials. Because no physical or chemical inactivation steps are involved in Saengsik manufacture, foodborne pathogens, such as B. cereus, which is a potential contaminant of the raw materials, could survive in the final product (Park, Koo, & Kim, 2019). Moreover, Saengsik is consumed after rehydration with cold water or milk; thus, it is inevitable that exposure to surviving foodborne pathogens, including B. cereus, pauses health risks to consumers. Thus, risk management of B. cereus in low-a_w foods, such as Saengsik, is needed to prevent foodborne outbreaks caused by pathogens of concern.

Mathematical models can describe bacterial behavior in food under various environmental conditions, including those of temperature and pH, and are thus essential for food safety management (Devlieghere, Francois, De Meulenaer, & Baert, 2006). Predictive models are used to evaluate microbial risk and develop appropriate intervention methods (Cassin, Paoli, & Lammerding, a M., 1998; Daelman et al., 2013; Ha et al., 2019). Various models have been developed to predict the growth or survival of B. cereus in cereal, dairy, meat, and vegetable-based foods, and culture media (Ellouze et al., 2021). Although B. cereus is a potential contaminant of low-a_w foods and can survive in powdered foods reconstituted with liquids such as juice or milk before consumption, no mathematical model for the organism has been reported (Jaquette & Beuchat, 1998). However, few studies have developed a mathematical model for the survival of B. cereus in powdered food with low a_w. A quantitative microbial risk assessment (QMRA) for B. cereus in powdered food has not been conducted, although a better understanding of improved food safety can be obtained using a risk assessment that includes hazard identification and food consumption scenarios using a stochastic modeling approach. Most studies on QMRA of B. cereus involved ready-to-eat products such as cooked rice, kimbap, rice cakes, etc. (Bahk, Todd, Hong, Oh, & Ha, 2007; Daelman et al., 2013; Kwon, Rhee, & Yoon, 2020; McElroy, Jaykus, & Foegeding, 1999; Park & Yoon, 2019).

In this study, a mathematical model for the survival of B. cereus in Saengsik products was developed as a function of temperature. The QMRA model was also developed using data on the concentration of B. cereus, time, and temperature along the retail-to-consumer processing stages. A predictive model was developed to estimate the probability of B. cereus infection after consuming Saengsik, a powdered food with very low-moisture content.

2 MATERIALS AND METHODS

2.1 Prevalence of B. cereus

To evaluate the contamination levels of B. cereus, Saengsik samples (n = 75) were purchased from retail markets and online shops in Korea. Twenty-five grams of powdered food samples were placed in sterile filter bags (Nasco, Fort Atkinson, WI, USA) and homogenized in 225 ml of 0.85% saline for 120 s at 230 rpm using Stomacher 400 (Seward, Worthing, UK), according to the Food Code (Ministry of Food and Drug Safety, 2022). Subsequently homogenate (1 ml) was serially diluted (10-fold) with saline, and 1 ml of each dilution suspension was spread onto mannitol egg yolk polymyxin agar plates (MYP, Merch, Darmstadt, Germany). Then, the plates were incubated at 30°C for 18–24 hr and the number of colonies were counted to calculate log CFU/g. Suspected colonies were confirmed using the VITEK2 BCL ID card (Biomérieux, Marcy-l'Étoile, France). Microbial data were obtained from three independent experiments performed in duplicate.

2.2 Inocula preparation

Three strains of B. cereus (KCCM 11204 [bceT and hbl], KCTC 1014 [nhe and entFM], and KCTC 1092 [bceT, hbl, nhe, entFM, and cytK and ces]) were obtained from the Korean Culture Center of Microorganisms (Seoul, Korea; KCCM 11204) and the Korean Collection for Type Cultures (Daejeon, Korea; KCTC 1014 and 1092). To develop the mathematical prediction model, a colony of each strain was cultured in 5 ml of tryptic soy broth (TSB, Merck) in sterile glass tubes in a shaking incubator at 140 rpm (SI-600R, Jeio Tech, Korea) at 30°C for 24 hr. Inocula (50 μl) of stationary phase grown cells were inoculated into 5 ml tubes containing sterile TSB broth and incubated at 30°C for 24 hr with agitation. The cultures were centrifuged at 2,111 × g for 10 min using an Eppendorf centrifuge 5804R (Eppendorf AG, Hamburg, Germany), and the supernatant was carefully removed. The cells were then washed twice and resuspended in phosphate-buffered saline (PBS, Gibco, Rockville, MD) to a final concentration of approximately 10⁷ CFU/ml. Bacterial suspension was serially diluted with PBS and was spread onto MYP at 30°C for 18–24 hr. The observed colonies were enumerated. Culture aliquots were mixed and used for inoculation.

2.3 Analysis of physicochemical properties

To develop and validate the predictive model, we analyzed the moisture content (Lee, Park, Park, & Kim, 2021), a_w and pH of Saengsik samples. The a_w was measured using the LabSwift-a_w system (Novasina, Zürich, Switzerland). Saengsik samples (10 g homogenized in 90 ml distilled water) pH was measured using an Orion Star A211 benchtop pH meter (Thermo Fisher Scientific, Waltham, MA). Physicochemical data were obtained from two independent experiments, and duplicate samples were used for each experiment.

2.4 Preparation of inoculated Saengsik samples

A previously described (Park et al., 2019) technique was followed to minimize changes in a_w of Saengsik inoculated with B. cereus cultures (Saengsik product A). B. cereus inoculum size was approximately 4.0 ± 0.5 log CFU/g. Inoculated Saengsik samples (10 g) were placed in an aluminum metalized polyethylene bag, normally used as packaging material for the product, and incubated at 5, 10, 20, 30, and 40°C for up to 10 days. Viable counts of B. cereus were carried out on samples taken after 0, 0.5, 1, 2, 3, 6, 12, 24, 48, 72, 144, and 240 hr. Into each sample bag, 90 ml of saline was added and homogenized. The serially diluted samples were plated on MYP agar and incubated at 30°C for 20 h. To obtain stable fitting data, we performed four to six replicate experiments in duplicate.

2.5 Development of primary and secondary model

The cell counts at each temperature were fitted into the Weibull model (Equation (1)) using the GInaFit V1.6 tool (Geeraerd, Valdramidis, & Van Impe, 2005) to determine the δ (delta, time of first decimal reduction) and p (a shape parameter) for microbial survival of B. cereus. The Weibull model (Equation (1)) was as follows:

N = N_{i} - ({(t / δ)}^{p})

(1)

where N is the number of cells (log CFU/g) at time t (h), N_i is the initial inoculum size of B. cereus (log CFU/g), δ (delta) is the simple dimension of time, which is the first decimal reduction time, and ρ is a shape parameter. For p > 1, convex curves were obtained, and for ρ < 1, concave curves were obtained (Geeraerd et al., 2005). The goodness-of-fit of the data was evaluated using coefficient of determination (R²) provided by GInaFiT.

Delta values and ρ values of the Weibull model were plotted as a function of temperature and fitted into the Davey model (Davey, 1991) and polynomial model, respectively. GraphPad Prism V 5.0 (GraphPad Software, San Diego, CA, USA) was used to assess the effect of temperature on the kinetic parameters of the primary survival curve (secondary survival model). Where a, b, and c are constants and T is the temperature.

δ = a + (b / T) + (c / T^{2})

(2)

2.6 Model validation

The developed predictive model was validated through additional experiments performed at 15 and 25°C. The observed data for 15 and 25°C were compared with the predicted data obtained from the developed predictive model. The differences between the observed and predicted data were quantified using the accuracy factor (A_f, Equation (3]), and bias factor (B_f, Equation [(4]), and root mean square error (RMSE, Equation [(5]) (Ross, 1996). The equations for A_f, B_f, and the RMSE are as follows:

A_{f} = 10^{\frac{1}{n} \sum |\log_{10} (\frac{predicted}{observed})|}

(3)

B_{f} = 10^{\frac{1}{n} \sum \log_{10} (\frac{predicted}{observed})}

(4)

RMSE = \sqrt{\frac{\sum {(observed - predicted)}^{2}}{n}}

(5)

The deviation between the observed and predicted values was evaluated by three indices: B_f, A_f, and RMSE. It is generally interpreted that B_f and A_f value of 0.9–1.05 is good, while values of 0.7–0.9 and 1.06–1.15 are acceptable ranges for predictive models. When A_f = B_f = 1, there is an exact match between the experimental observations and the model predictions (Ross, 1996). An RMSE value approaching zero indicated a closer fit of the model to the data. The validation data are representative of three to four individual experiments performed in duplicate.

2.7 Probabilistic risk modeling

To estimate the probability of infection by B. cereus from the consumption of Saengsik, the quantitative risk modeling framework comprised (i) food contamination amounts, (ii) cell number changes, and (iii) consumption amount and frequency, and minimum infectious dose was considered, as shown in Figure 1.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Schematic diagram for the microbial risk assessment of *Bacillus cereus* in *Saengsik*

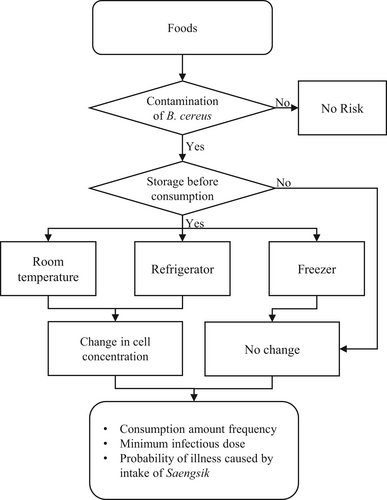
Data on the prevalence and survival of B. cereus in commercially available Saengsik products were obtained from this study to set the distribution parameters for the risk model. The prevalence data of B. cereus were fitted to the Beta distribution (α₁, the number of positive samples + 1; α₂, tested total samples—positive samples + 1) (Vose, 1998), and the initial contamination level (CFU/g) was then evaluated, using the equation: [–LN(1–Beta[α₁, α₂])/g] (Sanaa, Coroller, & Cerf, 2004). Other information to derive the distribution function, including time and temperature during retail to consumption, consumers' consumption amount and frequency of Saengsik, and minimum infectious dose for B. cereus, were obtained from previous studies (Ministry of Food and Drug Safety, 2012; 2016) or from experts' opinions.

The time and temperature for market storage were collected through personal communication with experts from the wholesale market (National Institute of Food and Drug Safety Evaluation, 2021). On average, Saengsik was kept at room temperature and sold out within 6 months (half of its shelf life). Thus, an appropriate probabilistic distribution for time and temperature in the market was a uniform distribution with parameters (0, 4,380) and (22, 24, 26) (Table 1). The transportation time from the market to home was at a minimum of 0.325 h and maximum of 1.643 h (Jung, 2011). In addition, the minimum, mean, and maximum temperatures during transportation were 9, 13.6, and 18.9°C, in Korea, respectively (Korea Meteorological Administration, 2019). We considered that Saengsik samples can be stored at home at room temperature or in the refrigerator before consumption, depending on consumer practices (Ministry of Food and Drug Safety, 2012). Saengsik is usually consumed within approximately 120 h at home and stored for up to 720 h at room temperature (Ministry of Food and Drug Safety, 2012). The temperature distribution of the home refrigerator was adopted from a previous work (Bahk, 2010). Thus, the appropriate distribution for the time, temperature at home (room temperature), and temperature of the home refrigerator were set to the Pert distribution with parameters (0, 245, and 8,760) and (15, 20, and 25), and RiskLoglogistic (−10.407, 13.616, 8.6107, RiskTruncate [−5.1, 14.4]), respectively (Table 1).

TABLE 1. Description of the variables

Input model	Unit	Variable	Formula	Reference
Product
Prevalence of Bacillus cereus		P_bc	Beta (1, 76)	Vose (1998)
Initial contamination level	Log CFU/g	D_i	log₁₀ (−LN[1 − P_bc]/25)	Sanaa et al. (2004)
Transport to retail
Transport temp	°C	T1	Risk Pert (3.5, 5.7, 10.5)	National Institute of Food and Drug Safety Evaluation (2019)
Transport time	h	t1	Risk Uniform (0.5, 5)	National Institute of Food and Drug Safety Evaluation (2019)
Delta		D1	−1,474 + (43,245/T1) + (249,956/T1^2)	This study
ρ		P1	1.257 − 0.3477 × T1 + 0.03435 × T1^2 − 0.001160 × T1^3 + 0.00001257 × T1^4	This study
Change level during transport to retail		C1	(t1/D1)^P1	Mafart, Couvert, Gaillard, and Leguerinel (2002)
Contamination level after transport to retail	Log CFU/g	D1	D_i − C1
Storage at retail warehouse
Storage temp	°C	T2	Risk Pert (22, 24, 26)	National Institute of Food and Drug Safety Evaluation (2019)
Storage time	h	t2	Risk Uniform (1/6, 48)	National Institute of Food and Drug Safety Evaluation (2019)
Delta		D2	−1,474 + (43,245/T2) + (249,956/T2^2)	This study
ρ		P2	1.257 − 0.3477 × T2 + 0.03435 × T2^2–0.001160 × T2^3 + 0.00001257 × T2^4	This study
Change level during storage at retail warehouse		C2	(t2/D2)^P2	Mafart et al. (2002)
Contamination level after storage at retail warehouse	Log CFU/g	D2	D1 − C2
In retail
Storage temp	°C	T3	Risk Pert (22, 24,26)	National Institute of Food and Drug Safety Evaluation (2019)
Storage time	h	t3	Risk Uniform (0, 4, 380)	National Institute of Food and Drug Safety Evaluation (2019)
Delta		D3	−1,474 + (43,245/T3) + (249,956/T3^2)	This study
ρ		P3	1.257 − 0.3477 × T3 + 0.03435 × T3^2–0.001160 × T3^3 + 0.00001257 × T3^4	This study
Change level during in retail		C3	(t3/D3)^P3	Mafart et al. (2002)
Contamination level in retail	Log CFU/g	D3	D2–C3
Transport to home
Transport temp	°C	T4	Risk Pert (9, 13.6, 18.9)	Korea Meteorological Administration (2019)
Transport time	h	t4	Risk Uniform (0.325, 1.643)	Jung (2011)
Delta		D4	−1,474 + (43,245/T4) + (249,956/T4^2)	This study
ρ		P4	1.257 − 0.3477 × T4 + 0.03435 × T4^2–0.001160 × T4^3 + 0.00001257 × T4^4	This study
Change level during transport to home		C4	(t4/D4)^P4	Mafart et al. (2002)
Contamination level after transport to home	Log CFU/g	D4	D3 − C4
Consumer practice
Ratio of consumption (without storage or consumption after storage at freezing)		R1	Risk Binomial(1, [0.3095 + 0.1667])	Ministry of Food and Drug Safety (2012)
Ratio of storage at refrigerator before consumption (from storage at room temperature and refrigerator)		R2	Risk Binomial (1, 0.750)	Ministry of Food and Drug Safety (2012)
Storage time before consumption	h	t5	Risk Pert (0, 245, 8,760)	Ministry of Food and Drug Safety (2012)
Home storage
Refrigerator temperature	°C	T6	Risk Loglogistic (−10.407, 13.616, 8.6107, Risk Truncate [−5.1, 14.4])	Bahk (2010)
Delta		D6	−1,474 + (43,245/T6) + (249,956/T6^2)	This study
ρ		P6	−1.257 − 0.3477 × T6 + 0.03435 × T6^2–0.001160 × T6^3 + 0.00001257 × T6^4	This study
Change level during storage at refrigerator	Log CFU/g	C6	(t5/D6)^P6	Mafart et al. (2002)
Contamination level after storage at refrigerator	Log CFU/g	D6	D4 − C6
Room temperature	°C	T7	Risk Pert (15, 20, 25)	National Institute of Food and Drug Safety Evaluation (2019)
Delta		D7	−1,474 + (43,245/T7) + (249,956/T7^2)	This study
ρ		P7	1.257 − 0.3477 × T7 + 0.03435 × T7^2 − 0.001160 × T7^3 + 0.00001257 × T7^4	This study
Change level during storage at room temp	Log CFU/g	C7	(t5/D7)^P7	Mafart et al. (2002)
Contamination level after storage at room temp	Log CFU/g	D7	Dth − Crt
Concentration considering consumer practice on storage before consumption	Log CFU/g	Cr	=IF(R1 = 1,D4,Cs)
Concentration change (room temp or refrigerator)	Log CFU/g	Cs	=IF(R2 = 1, D6, D7)
Concentration considering consumer practice on storage before consumption	CFU/g	Ci	=10^Cr
Consumption
Daily consumption (consumer)	g	Consump	Risk Log logistics (−8.9743, 52.272, 6.4020, risk truncate [0, 200])	Ministry of Food and Drug Safety (2012)
Daily consumption frequency	%		Fixed 8.5071	Ministry of Food and Drug Safety (2012)
A person who does not eating Saengsik		CF(0)	1–8.5071/100	Ministry of Food and Drug Safety (2012)
A person eating Saengsik		CF(1)	8.5071/100	Ministry of Food and Drug Safety (2012)
		CF	Risk Discrete ([0, 1], [CF(0)], CF[1])	Ministry of Food and Drug Safety (2012)
Daily consumption (total)		ConFre	If(CF = 0, 0, Consump)	Ministry of Food and Drug Safety (2012)
Dose–response
B. cereus amount (consumed)	CFU/g	D	Ci × Confre
Probability of illness/serving		Risk	If(D > 100,000, 1, 0)

The consumption amount of Saengsik were described as a probabilistic distribution. According to a report by the Ministry of Food and Drug Safety in Korea (Ministry of Food and Drug Safety, 2012), the daily consumption frequency of Saengsik was 8.51% and the daily consumption amount was fitted to the LogLogistics distribution. The distribution function for the daily consumption amount was derived using the best-fit function in the @Risk program (version 8.0, Palisade Corp., Ithaca, NY, USA). The average daily consumption of Saengsik was 47.94 ± 21.92 g per serving.

For the last phase of risk modeling, hazard characterization was conducted using the minimum infectious dose of B. cereus to estimate the probability of infection because a dose–response model for B. cereus has not been developed (Ministry of Food and Drug Safety, 2016). In previous reports, 10⁵ cells/g was found as the minimal infectious dose (Park, Cho, Lee, & Bahk, 2014). Thus, we assumed that exposure to 10⁵ CFU or more of B. cereus cells per person per day would result in disease (1), and any dose below that would not cause disease (0).

To build a probabilistic exposure model, @Risk program (version 8.0; Palisade, Ithaca, NY) was used to perform Monte Carlo simulations with 100,000 iterations.

2.8 Growth of B. cereus in reconstituted Saengsik

Saengsik samples (20 g) were added to 80 ml sterile distilled water and mixed by shaking, according to the manufacturer's recommendations. B. cereus cells were added at a concentration of 2.5 ± 0.5 log CFU/g, then incubated at 5, 20, 30°C for 24 h. The viable count of the organism for each inoculated Saengsik sample at each incubation temperature was determined.

3 RESULTS AND DISCUSSION

3.1 Prevalence of B. cereus

All the 75 Saengsik samples were analyzed below the detection limit of B. cereus. The initial contamination level was estimated from these prevalence data with a beta distribution and the calculation formula reported by Sanaa and others using @Risk (Sanaa et al., 2004). The initial level of B. cereus contamination in Saengsik was a minimum of −7.6, an average of −3.5, and a maximum of −2.3 log CFU/g, indicating that the initial potential infection level of B. cereus was very low (Figure S1). Similar results have been noted in previous reports (Choi et al., 2021; Ha et al., 2019; Kwon et al., 2020; Lee et al., 2019).

3.2 Development of predictive model and validation

The predictive model was developed using Saengsik product. The moisture content, pH, and a_w were 2.8 ± 0.2%, pH 6.55, a_w < 0.1, respectively. The bacterial survival patterns and the primary survival model of B. cereus in Saengsik incubated at different temperatures are shown in Figure 2. The delta and ρ values calculated from the Weibull model used to develop the primary survival prediction model are listed in Table 2. Storage temperatures at 5, 10, 20, 30, and 40°C, the delta values were 17,124.05, 5,695.95, 603.83, 292.54, and 128.63 h, respectively. At all storage temperatures studied, the ρ value was <1, indicating a concave-shaped survival pattern. The inactivation kinetics of B. cereus, which decreased with increasing temperature, was undoubtedly temperature dependent. However, B. cereus was not dramatically decreased compared with other strains, such as a spore forming bacterium Clostridium perfringens (Choi et al., 2021; Park et al., 2019). When incubated at 40°C for 24 h, the viability of B. cereus in Saengsik samples decreased by approximately 1 log CFU/g (Figure 2e). The delta obtained from the primary model was used to develop a secondary model for the function of temperature using the Davey model (Davey, 1991). The developed secondary model is shown in Figure 2f, and Table 3. The R² value of the secondary model of delta and ρ value for B. cereus in Saengsik was 0.996 and 1.000, respectively. Indicating that the secondary models were appropriate for describing the effects of temperature on the kinetic parameters.

TABLE 2. Kinetic parameters calculated by the Weibull model for Bacillus cereus survival in Saengsik during storage at 5, 10, 20, 30 and 40°C

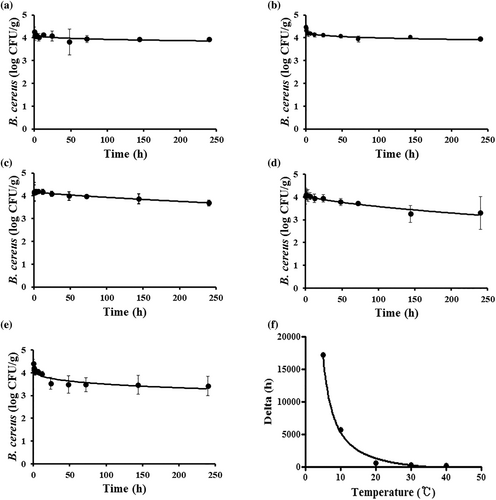
Storage temperature (°C)	Weibull model
Storage temperature (°C)	Delta	ρ	N₀	R²
5	17,124.05	0.24	4.22	0.656
10	5,695.95	0.18	4.48	0.874
20	603.83	0.77	4.18	0.964
30	292.54	0.59	4.15	0.973
40	128.63	0.22	4.44	0.903

Note: Delta, time for the first decimal reduction (h); ρ, shape; N₀, initial contamination level (log CFU/g).

TABLE 3. Secondary model for Bacillus cereus survival in Saengsik as a function of storage temperature

Parameter	Equation	R²
Delta	Y = −1,474 + (43,245/Temperature) + (249,956/Temperature²)	0.996
ρ	Y = 1.257−0.3477 × Temperature + 0.03435 × Temperature²−0.001160 × Temperature³ + 0.00001257 × Temperature⁴	1.000

The developed secondary model was validated using temperatures that were not used for model development. By conducting additional storage experiments at temperatures of 15 and 25°C to verify the model for predicting survival of B. cereus in Saengsik, the developed model was found suitable for a B_f value of 1.008, A_f value of 1.012, and an RMSE value of 0.069 (Figure 3a). Figure 3b shows a comparison of cell number for B. cereus between observed values and predicted values. The predicted values were well correlated with the observed bacterial cell numbers.

3.3 Probabilistic risk assessment for consumption of Saengsik

The Monte Carlo simulation showed that the probability of food poisoning caused by B. cereus was estimated to be zero under the current contamination level, distribution conditions, and consumption patterns. Therefore, it is reasonable to assume that the risk of B. cereus foodborne illness due to the consumption of low-moisture powdered Saengsik food is very low. Our results are in agreement with a study (Ha et al., 2019) showing low risk of foodborne pathogens due to C. jejuni in beef jerky, which is also a low-moisture food. In a previous study on modeling the risk of salmonellosis after consuming pistachios, most pistachios were not contaminated Salmonella and hence carry zero probability of illness (Lambertini, Barouei, Schaffner, Danyluk, & Harris, 2017). The simulation results of this study showed that the probability of infection was estimated to be zero. Guidelines of B. cereus contamination level in Saengsik products in the Food Code in Korea support the very low risk of B. cereus infection due to consumption of Saengsik products. The Food Code in Korea allows the detection level of B. cereus in Saengsik products as less than 3 log CFU/g (Ministry of Food and Drug Safety, 2022). The risk assessment obtained in this study was based on limited data. It is, therefore, necessary to continuously perform risk assessment to establish a risk-based microbial standard if additional data are produced.

3.4 Growth of B. cereus in reconstituted Saengsik

Although we observed a very low risk of B. cereus infection from the consumption of Saengsik, possible bacterial growth in the reconstituted Saengsik with water or milk, which was not consumed immediately, cannot be neglected. Thus, growth and survival curve of B. cereus in Saengsik reconstituted with water was evaluated. When inoculated samples were stored at 5°C for 12 h, growth of B. cereus was not observed (Figure 4). However, if inoculated Saengsik samples with an amount of serving size (52.27 g) were kept at 20°C for 4 h, B. cereus population growth (Figure 4) exceeded the assumed infective dose (10⁵ CFU/g). Furthermore, storage at 30°C required only 2 h to reach infectious dose amount. In a previous study, C. perfringens did not grow in reconstituted Saengsik stored at 20°C (Park et al., 2019); however, in this study, B. cereus count reached the infectious amount within 4 h at 20°C (serving size of 52.27 g was considered). This study has some limitations. The microbial growth model of the reconstituted Saengsik was not incorporated in QMRA because the lack of data on the holding temperatures and time of reconstituted Saengsik in the consumer's behavior survey. Under the currently available data, it does not seem desirable to insert growth model of reconstituted Saengsik into QMRA because many assumptions have to be involved. This result shows that microorganisms can grow rapidly when powdered food is reconstituted. It is, therefore, recommended that reconstituted Saengsik be consumed as fast as possible or be kept refrigerated to avoid any health risks. Further study is needed to describe the consumers' behavior to handle the reconstituted Saengsik before consumption.

**FIGURE 4**
Open in figure viewer PowerPoint

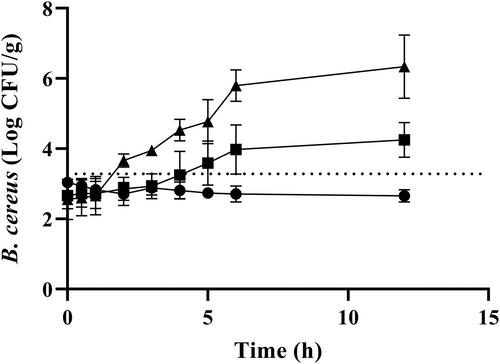
Growth kinetics of *Bacillus cereus* in *Saengsik* prepared according to the manufacturer's recommendations for the consumption and stored at various temperatures: 5, 20, and 30°C. The dotted line represents the number of *B. cereus* to reach 10⁵ CFU/g in an average single serving size of *Saengsik* (52.27 g)

4 CONCLUSION

Long-term survival of foodborne pathogens, especially B. cereus, in low-moisture foods is a concern in the food industry. Mathematical modeling of the behavior of B. cereus and probabilistic modeling for the risk of B. cereus in very low-moisture food are required before the development of safety management technologies. In this study, grain-based Saengsik products with very low-a_w were selected as a model for low-moisture food. A survival model of B. cereus was developed and it was found that it can survive well in low-moisture food, suggesting that control of initial contamination of raw materials is crucial. Despite a lack of prior information, a predictive model of B. cereus in very low-a_w food was developed that can be applied to the safety management of low-moisture food in the food industry. Although the estimated probability of B. cereus infection was zero when using the baseline model with currently available data, the developed QMRA model may help identify intervention steps to further reduce the risk of foodborne illness for low-moisture food. When reconstituted Saengsik samples were stored at 20°C or 30°C, B. cereus grew rapidly. The growth patterns of B. cereus in reconstituted samples should therefore provide important insight when setting consumer guidelines, that is, consumers should refrigerate or immediately consume reconstituted Saengsik to avoid potential health hazards. During this study, data gaps regarding consumers' handling of reconstituted Saengsik samples were identified, including storage time and temperature before consumption of reconstituted Saengsik at home. Further study is needed on the holding time and temperatures of reconstituted Saengsik at home and dose–response model of B. cereus. These results provide useful information for the risk assessment and management of microbial risk in foods, especially in foods with very low-moisture contents.

ACKNOWLEDGMENTS

This research was supported by a grant from the Ministry of Food and Drug Safety (17162MFDS035).

CONFLICTS OF INTEREST

The authors declare no conflicts of interest.

Open Research

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supporting Information

REFERENCES

Bahk, G. J. (2010). Statistical probability analysis of storage temperatures of domestic refrigerator as a risk factor of foodborne illness outbreak. Korean Journal of Food Science and Technology, 42(3), 373–376.
Google Scholar
Bahk, G.-J., Todd, E. C. D., Hong, C.-H., Oh, D.-H., & Ha, S.-D. (2007). Exposure assessment for Bacillus cereus in ready-to-eat Kimbab selling at stores. Food Control, 18(6), 682–688. https://doi.org/10.1016/j.foodcont.2006.02.017
10.1016/j.foodcont.2006.02.017
Web of Science® Google Scholar
Bourdichon, F., Betts, R., Dufour, C., Fanning, S., Farber, J., McClure, P., … Winkler, A. (2021). Processing environment monitoring in low moisture food production facilities: Are we looking for the right microorganisms? International Journal of Food Microbiology, 356, 109351. https://doi.org/10.1016/j.ijfoodmicro.2021.109351
10.1016/j.ijfoodmicro.2021.109351
PubMed Web of Science® Google Scholar
Cassin, M. H., Paoli, G. M., & Lammerding, A. M. (1998). Simulation modeling for microbial risk assessment. Journal of Food Protection, 61(11), 1560–1566.
10.4315/0362-028X-61.11.1560
CAS PubMed Web of Science® Google Scholar
Choi, W., & Kim, S.-S. (2020). Outbreaks, germination, and inactivation of Bacillus cereus in food products: A review. Journal of Food Protection, 83(9), 1480–1487. https://doi.org/10.4315/0362-028X.JFP-19-429
10.4315/0362-028X.JFP-19-429
CAS PubMed Web of Science® Google Scholar
Choi, Y. H., Park, J. H., Kang, M. S., Yoon, Y., Ha, S., & Kim, H. J. (2021). Predictive modeling and probabilistic risk assessment of Clostridium perfringens in hamburgers and sandwiches. Food Science and Biotechnology, 30(13), 1733–1742. https://doi.org/10.1007/s10068-021-01000-z
10.1007/s10068-021-01000-z
CAS PubMed Web of Science® Google Scholar
Daelman, J., Membré, J.-M., Jacxsens, L., Vermeulen, A., Devlieghere, F., & Uyttendaele, M. (2013). A quantitative microbiological exposure assessment model for Bacillus cereus in REPFEDs. International Journal of Food Microbiology, 166(3), 433–449. https://doi.org/10.1016/j.ijfoodmicro.2013.08.004
10.1016/j.ijfoodmicro.2013.08.004
PubMed Web of Science® Google Scholar
Davey, K. R. (1991). Applicability of the Davey (linear Arrhenius) predictive model to the lag phase of microbial growth. Journal of Applied Bacteriology, 70(3), 253–257. https://doi.org/10.1111/j.1365-2672.1991.tb02933.x
10.1111/j.1365-2672.1991.tb02933.x
Web of Science® Google Scholar
Devlieghere, F., Francois, K., De Meulenaer, B., & Baert, K. (2006). Modelling food safety. In Safety in the agri-food chain (pp. 397–437). Wageningen: Wageningen Academic Publishers.
Google Scholar
EFSA and ECDC. (2019). The European Union one health 2018 Zoonoses report. EFSA Journal, 17(12), e05926. https://doi.org/10.2903/j.efsa.2019.5926
10.2903/j.efsa.2019.5926
PubMed Web of Science® Google Scholar
Ellouze, M., Buss Da Silva, N., Rouzeau-Szynalski, K., Coisne, L., Cantergiani, F., & Baranyi, J. (2021). Modeling Bacillus cereus growth and Cereulide formation in cereal-, dairy-, meat-, vegetable-based food and culture medium. Frontiers in Microbiology, 12, 639546. https://doi.org/10.3389/fmicb.2021.639546
10.3389/fmicb.2021.639546
PubMed Web of Science® Google Scholar
Galié, S., García-Gutiérrez, C., Miguélez, E. M., Villar, C. J., & Lombó, F. (2018). Biofilms in the food industry: Health aspects and control methods. Frontiers in Microbiology, 9, 898. https://doi.org/10.3389/fmicb.2018.00898
10.3389/fmicb.2018.00898
PubMed Web of Science® Google Scholar
Geeraerd, A. H., Valdramidis, V. P., & Van Impe, J. F. (2005). GInaFiT, a freeware tool to assess non-log-linear microbial survivor curves. International Journal of Food Microbiology, 102(1), 95–105. https://doi.org/10.1016/j.ijfoodmicro.2004.11.038
10.1016/j.ijfoodmicro.2004.11.038
CAS PubMed Web of Science® Google Scholar
Giaouris, E. E., & Simões, M. V. (2018). Chapter 11 - Pathogenic biofilm formation in the food industry and alternative control strategies. In Handbook of food bioengineering (pp. 309–377). Cambridge, MA: Academic Press. https://doi.org/10.1016/B978-0-12-811444-5.00011-7
Google Scholar
Ha, J., Lee, H., Kim, S., Lee, J., Lee, S., Choi, Y., … Yoon, Y. (2019). Quantitative microbial risk assessment of Campylobacter jejuni in jerky in Korea. Asian-Australasian Journal of Animal Sciences, 32(2), 274–281. https://doi.org/10.5713/ajas.18.0322
10.5713/ajas.18.0322
CAS PubMed Web of Science® Google Scholar
Jaquette, C. B., & Beuchat, L. R. (1998). Survival and growth of psychrotrophic Bacillus cereus in dry and reconstituted infant rice cereal. Journal of Food Protection, 61(12), 1629–1635 http://meridian.allenpress.com/jfp/article-pdf/61/12/1629/1663847/0362-028x-61_12_1629.pdf
10.4315/0362-028X-61.12.1629
CAS PubMed Web of Science® Google Scholar
Jung, H. (2011). Consumer survey and hazard analysis for the improvement of food hygiene and safety in purchase. (Degree of master's dissertation). Korea University, Seoul, South Korea.
Google Scholar
Korea Meteorological Administration. (2019). Korea Meteorological Administration (Issue 11). https://data.kma.go.kr/data/grnd/selectAsosList.do?pgmNo=34
Google Scholar
Kwon, M. J., Rhee, M. S., & Yoon, K. S. (2020). A risk assessment study of Bacillus cereus in packaged tofu at a retail market in Korea. Food Science and Biotechnology, 29(3), 339–350. https://doi.org/10.1007/s10068-019-00670-0
10.1007/s10068-019-00670-0
CAS PubMed Web of Science® Google Scholar
Lambertini, E., Barouei, J., Schaffner, D. W., Danyluk, M. D., & Harris, L. J. (2017). Modeling the risk of salmonellosis from consumption of pistachios produced and consumed in the United States. Food Microbiology, 67, 85–96. https://doi.org/10.1016/j.fm.2017.06.003
10.1016/j.fm.2017.06.003
PubMed Web of Science® Google Scholar
Lee, H., Park, J. H., Park, Y. K., & Kim, H. J. (2021). Mathematical modeling for the growth of Salmonella spp. and Staphylococcus aureus in cake at fluctuating temperatures. Applied Sciences, 11(6), 2475. https://doi.org/10.3390/app11062475
10.3390/app11062475
CAS Google Scholar
Lee, J., Lee, H., Lee, S., Kim, S., Ha, J., Choi, Y., … Yoon, Y. (2019). Quantitative microbial risk assessment for Campylobacter jejuni in ground meat products in Korea. Food Science of Animal Resources, 39(4), 565–575. https://doi.org/10.5851/kosfa.2019.e39
10.5851/kosfa.2019.e39
PubMed Web of Science® Google Scholar
Mafart, P., Couvert, O., Gaillard, S., & Leguerinel, I. (2002). On calculating sterility in thermal preservation methods: Application of the Weibull frequency distribution model. International Journal of Food Microbiology, 72, 107–113.
10.1016/S0168-1605(01)00624-9
CAS PubMed Web of Science® Google Scholar
McElroy, D. M., Jaykus, L. A., & Foegeding, P. M. (1999). Quantitative risk assessment for Bacillus cereus emetic disease associated with the consumption of Chinese-style rice. Journal of Food Safety, 19, 209–229.
10.1111/j.1745-4565.1999.tb00246.x
Web of Science® Google Scholar
Ministry of Food and Drug Safety. (2012). 50 major food intake amount and patterns for microbial risk assessment. Ministry of Food and Drug Safety.
Google Scholar
Ministry of Food and Drug Safety. (2016). Understanding of microbial risk assessment for emergency response.
Google Scholar
Ministry of Food and Drug Safety. (2020). Food poisoning statistics. Ministry of Food and Drug Safety. https://www.foodsafetykorea.go.kr/portal/healthyfoodlife/foodPoisoningStat.do?menu_no=4425
Google Scholar
Ministry of Food and Drug Safety. (2022). Food code. Ministry of Food and Drug Safety. https://www.mfds.go.kr/eng/brd/m_15/view.do?seq=69982
Google Scholar
National Institute of Food and Drug Safety Evaluation. (2019). Risk assessment of Clostridium perfringens in red pepper powder, Shredded Red Pepper and Composite Seasonings. National Institute of Food and Drug Safety Evaluation.
Google Scholar
National Institute of Food and Drug Safety Evaluation. (2021). Risk assessment of Clostridium perfringens in raw foods(Saengsik) (Issue June). http://www.nifds.go.kr/brd/m_271/view.do?seq=12557&srchFr=&srchTo=&srchWord=&srchTp=&itm_seq_1=0&itm_seq_2=0&multi_itm_seq=0&company_cd=&company_nm=&page=1
Google Scholar
Osimani, A., Aquilanti, L., & Clementi, F. (2018). Bacillus cereus foodborne outbreaks in mass catering. International Journal of Hospitality Management, 72, 145–153. https://doi.org/10.1016/j.ijhm.2018.01.013
10.1016/j.ijhm.2018.01.013
Web of Science® Google Scholar
Park, H. W., & Yoon, W. B. (2019). A quantitative microbiological exposure assessment model for Bacillus cereus in pasteurized rice cakes using computational fluid dynamics and Monte Carlo simulation. Food Research International, 125, 108562. https://doi.org/10.1016/j.foodres.2019.108562
10.1016/j.foodres.2019.108562
CAS PubMed Web of Science® Google Scholar
Park, J. H., Koo, M., & Kim, H. J. (2019). Modeling for survival of Clostridium perfringens in Saeng-sik, a powdered ready-to-eat food with low water activity. Journal of Food Protection, 82(7), 1141–1147. https://doi.org/10.4315/0362-028X.JFP-18-368
10.4315/0362-028X.JFP-18-368
CAS PubMed Web of Science® Google Scholar
Park, M. S., Cho, J. I., Lee, S. H., & Bahk, G. J. (2014). The analysis for minimum infective dose of foodborne disease pathogens by meta-analysis. Journal of Food Hygiene and Safety, 29(4), 305–311. doi.10.13103/jfhs.2014.29.4.305
10.13103/JFHS.2014.29.4.305
Google Scholar
Ray, B., & Bhunia, A. (2013). Fundamental food microbiology ( 5th ed.). Boca Raton, FL: Taylor & Francis https://books.google.co.kr/books?id=NXr6AQAAQBAJ
10.1201/b16078
Google Scholar
Reiji, H., Masakado, M., Kenji, S., & Yutaka, M. (2005). Ability of Shiga toxin-producing Escherichia coli and Salmonella spp. to survive in a desiccation model system and in dry foods. Applied and Environmental Microbiology, 71(11), 6657–6663. https://doi.org/10.1128/AEM.71.11.6657-6663.2005
10.1128/AEM.71.11.6657-6663.2005
PubMed Web of Science® Google Scholar
Ross, T. (1996). Indices for performance evaluation of predictive models in food microbiology. Journal of Applied Bacteriology, 81(5), 501–508. https://doi.org/10.1111/j.1365-2672.1996.tb03539.x
10.1111/j.1365-2672.1996.tb03539.x
CAS PubMed Web of Science® Google Scholar
Rouzeau-Szynalski, K., Stollewerk, K., Messelhäusser, U., & Ehling-Schulz, M. (2020). Why be serious about emetic Bacillus cereus: Cereulide production and industrial challenges. Food Microbiology, 85, 103279. https://doi.org/10.1016/j.fm.2019.103279
10.1016/j.fm.2019.103279
CAS PubMed Web of Science® Google Scholar
Sanaa, M., Coroller, L., & Cerf, O. (2004). Risk assessment of listeriosis linked to the consumption of two soft cheeses made from raw milk: Camembert of Normandy and Brie of Meaux. Risk Analysis: An International Journal, 24(2), 389–399.
10.1111/j.0272-4332.2004.00440.x
PubMed Web of Science® Google Scholar
Sánchez-Maldonado, A. F., Lee, A., & Farber, J. M. (2018). Methods for the control of foodborne pathogens in low-moisture foods. Annual Review of Food Science and Technology, 9(1), 177–208. https://doi.org/10.1146/annurev-food-030117-012304
10.1146/annurev-food-030117-012304
CAS PubMed Web of Science® Google Scholar
Thirkell, C. E., Sloan-Gardner, T. S., Kacmarek, M. C., & Polkinghorne, B. (2019). An outbreak of Bacillus cereus toxin-mediated emetic and diarrhoeal syndromes at a restaurant in Canberra, Australia 2018. Communicable Diseases Intelligence, 2018, 43. https://doi.org/10.33321/CDI.2019.43.40
10.33321/CDI.2019.43.40
Web of Science® Google Scholar
Vose, D. J. (1998). The application of quantitative risk assessment to microbial food safety. Journal of Food Protection, 61(5), 640–648.
10.4315/0362-028X-61.5.640
CAS PubMed Web of Science® Google Scholar

Volume43, Issue1

February 2023

e13025

Mathematical modeling of Bacillus cereus in Saengsik, a powdered ready-to-eat food and its application in quantitative microbial risk assessment

Abstract

1 INTRODUCTION