Hierarchical Structure Recovery of Point-Sampled Surfaces
Marco Attene
Istituto di Matematica Applicata e Tecnologie Informatiche, Consiglio Nazionale delle Ricerche, Italy [email protected] , [email protected]
Search for more papers by this authorGiuseppe Patanè
Istituto di Matematica Applicata e Tecnologie Informatiche, Consiglio Nazionale delle Ricerche, Italy [email protected] , [email protected]
Search for more papers by this authorMarco Attene
Istituto di Matematica Applicata e Tecnologie Informatiche, Consiglio Nazionale delle Ricerche, Italy [email protected] , [email protected]
Search for more papers by this authorGiuseppe Patanè
Istituto di Matematica Applicata e Tecnologie Informatiche, Consiglio Nazionale delle Ricerche, Italy [email protected] , [email protected]
Search for more papers by this authorAbstract
We focus on the class of ‘regular’ models defined by Várady et al. for reverse engineering purposes. Given a 3D surface 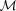 represented through a dense set of points, we present a novel algorithm that converts
represented through a dense set of points, we present a novel algorithm that converts 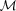 to a hierarchical representation
to a hierarchical representation 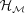 . In
. In 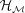 , the surface is encoded through patches of various shape and size, which form a hierarchical atlas. If
, the surface is encoded through patches of various shape and size, which form a hierarchical atlas. If  belongs to the class of regular models, then
belongs to the class of regular models, then 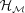 captures the most significant features of
captures the most significant features of 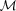 at all the levels of detail. In this case, we show that
at all the levels of detail. In this case, we show that 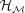 can be exploited to interactively select regions of interest on
can be exploited to interactively select regions of interest on 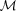 and intuitively re-design the model. Furthermore,
and intuitively re-design the model. Furthermore, 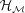 intrinsically encodes a hierarchy of useful ‘segmentations’ of
intrinsically encodes a hierarchy of useful ‘segmentations’ of 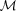 . We present a simple though efficient approach to extract and optimize such segmentations, and we show how they can be used to approximate the input point sets through idealized manifold meshes.
. We present a simple though efficient approach to extract and optimize such segmentations, and we show how they can be used to approximate the input point sets through idealized manifold meshes.
References
- [AA03] Adamson A., Alexa M.: Approximating and intersecting surfaces from points. In Symp. on Geometry Processing (2003), pp. 230–239.
- [ABCO*01] Alexa M., Behr J., Cohen-Or D., Fleishman S., Levin D., Silva C. T.: Point set surfaces. In IEEE Visualization (2001), pp. 21–28.
- [AF06] Attene M., Falcidieno B.: Remesh: An interactive environment to edit and repair triangle meshes. In Shape Modeling and Applications (2006), pp. 271–276.
- [AFRS05] Attene M., Falcidieno B., Rossignac J., Spagnuolo M.: Sharpen and bend: Recovering curved sharp edges in triangle meshes produced by feature-insensitive sampling. IEEE Trans. on Visualiz. and Comp. Graphics 11, 2 (2005), 181–192.
- [AFS06] Attene M., Falcidieno B., Spagnuolo M.: Hierarchical mesh segmentation based on fitting primitives. The Visual Computer 22, 3 (2006), 181–193.
- [AGP*04] Alexa M., Gross M., Pauly M., Pfister H., Stamminger M., Zwicker M.: Point-based computer graphics. In ACM Siggraph Course Notes (2004).
- [AK04] Amenta N., Kil Y. J.: Defining point-set surfaces. In ACM Siggraph (2004), pp. 264–270.
- [AKM*06] Attene M., Katz S., Mortara M., Patane G., Spagnuolo M., Tal A.: Mesh segmentation - a comparative study. In Proc. of the IEEE Shape Modeling and Applications (2006), p. 7.
- [AMN*98] Arya S., Mount D. M., Netanyahu N. S., Silverman R., Wu A. Y.: An optimal algorithm for approximate nearest neighbor searching fixed dimensions. Journal of the ACM 45, 6 (1998), 891–923.
- [AMSF08] Attene M., Mortara M., Spagnuolo M., Falcidieno B.: Hierarchical convex approximation for fast region selection. Computer Graphics Forum 27, 5 (2008), 1323–1333.
- [APP*07]
Agathos A.,
Pratikakis I.,
Perantonis S.,
Sapidis N.,
Azariadis P.: 3D mesh segmentation methodologies for cad applications.
Computer-Aided Design and Applications
4, 6 (2007), 827–841.
10.1080/16864360.2007.10738515 Google Scholar
- [BS95] Barequet G., Sharir M.: Filling gaps in the boundary of a polyhedron. Computer-Aided Geometric Design 12, 2 (1995), 207–229.
- [BSRS04] Bespalov D., Shokoufandeh A., Regli W. C., Sun W.: Local feature extraction using scale-space decomposition. In Design Engineering Technical Conferences (2004).
- [CDST97] Chazelle B., Dobkin D., Shourhura N., Tal A.: Strategies for polyhedral surface decomposition: An experimental study. Computational Geometry: Theory and Applications 7, 4-5 (1997), 327–342.
- [CG01] Chaperon T., Goulette F.: Extracting cylinders in full 3D data using a random sampling method and the gaussian image. In Vision Modeling and Visualization (2001), pp. 35–42.
- [CSAD04] Cohen-Steiner D., Alliez P., Desbrun M.: Variational shape approximation. ACM Transactions on Graphics 23, 3 (2004), 905–914.
- [DGG03] Dey T. K., Giesen J., Goswami S.: Shape segmentation and matching with flow discretization. Lecture Notes in Computer Science 2748 (2003), 25–36.
- [DKT05]
Desbrun M.,
Kanso E.,
Tong Y.: Discrete differential forms for computational modeling. In
ACM Siggraph 2005 Courses (2005), p.
7.
10.1145/1198555.1198666 Google Scholar
- [DS05] Dey T. K., Sun J.: An adaptive MLS surface for reconstruction with guarantees. In Symp. on Geometry Processing (2005), pp. 43–52.
- [FCOAS03] Fleishman S., Cohen-Or D., Alexa M., Silva C. T.: Progressive point set surfaces. ACM Transactions on Graphics 22, 4 (2003), 997–1011.
- [FKS*04] Funkhouser T., Kazhdan M., Shilane P., Min P., Kiefer W., Tal A., Rusinkiewicz S., Dobkin D.: Modeling by example. ACM Transactions on Graphics 23, 3 (2004), 652–663.
- [GG04] Gelfand N., Guibas L. J.: Shape segmentation using local slippage analysis. In Symp. on Geometry Processing (2004), pp. 214–223.
- [GG07] Guennebaud G., Gross M.: Algebraic point set surfaces. In ACM Transactions on Graphics 26 (2007), p. 23.
- [GKS00] Gopi M., Krishnan S., Silva C.: Surface reconstruction based on lower dimensional localized delaunay triangulation. Computer Graphics Forum 19, 3 (2000), 467–478.
- [GPA*02] Gross M., Pfister H., Alexa M., Pauly M., Stamminger M., Zwicker M.: Point-based computer graphics. Eurographics Tutorial, 2002.
- [GWH01] Garland M., Willmott A., Heckbert P.: Hierarchical face clustering on polygonal surfaces. In ACM Symp. on Interactive 3D Graphics (2001), pp. 49–58.
- [HDD*94] Hoppe H., DeRose T., Duchamp T., Halstead M., Jin H., McDonald J., Schweitzer J., Stuetzle W.: Piecewise smooth surface reconstruction. In Computer Graphics and Interactive Techniques (1994), pp. 295–302.
- [ITY*01] Inoue K., Takayuki I. Y. A., Tomotake F., Kenji S.: Face clustering of a large-scale cad model for surface mesh generation. Computer-Aided Design 33 (2001), 251–261.
- [KL87] Kelker D., Langenberg C. W.: A mathematical model for orientation data from macroscopic elliptical conical folds. Mathematical Geology 19, 8 (1987), 729–743.
- [KT03] Katz S., Tal A.: Hierarchical mesh decomposition using fuzzy clustering and cuts. ACM Transactions on Graphics 22, 3 (2003), 954–961.
- [Lev03] Levin D.: Mesh-independent surface interpolation. Geometric Modeling for Scientific Visualization 3 (2003), 37–49.
- [LJS97] Leonardis A., Jaklic A., Solina F.: Superquadrics for segmenting and modeling range data. IEEE Transactions on Pattern Analysis and Machine Intelligence 19 (1997), 1289–1295.
- [LLS*05] Lee Y., Lee S., Shamir A., Cohen-Or D., Seidel H.-P.: Mesh scissoring with minima rule and part salience. Computer Aided Geometric Design 22, 5 (2005), 444–465.
- [LMM98]
Lukács G.,
Martin R.,
Marshall D.: Faithful least-squares fitting of spheres, cylinders, cones and tori for reliable segmentation.
Lecture Note in Computer Science, Computer Vision
1406, 1 (1998), 671–686.
10.1007/BFb0055697 Google Scholar
- [LP05] Lange C., Polthier K.: Anisotropic smoothing of point sets. Computer Aided Geometric Design 22, 7 (2005), 680–692.
- [LSA94] Leonardis A., Solina F., Alenka M.: A direct recovery of super-quadric models in range images using recover-and-select paradigm. In Proc. of Conf. on Computer Vision (1994), pp. 309–318.
- [LZ04] Liu R., Zhang H.: Segmentation of 3D meshes through spectral clustering. In Pacific Graphics (2004), pp. 298–305.
- [Mar82] Marr D.: Vision. Freeman Publishers, New York , 1982.
- [MFX*07] Miao Y.-W., Feng J.-Q., Xiao C.-X., Peng Q.-S., Forrest A. R.: Differentials-based segmentation and parameterization for point-sampled surfaces. Journal of Computer Science and Technology 22, 5 (2007), 749–760.
- [MPS*03] Mortara M., Patanè G., Spagnuolo M., Falcidieno B., Rossignac J.: Blowing bubbles for multi-scale analysis and decomposition of triangle meshes. Algorithmica 38, 1 (2003), 227–248.
- [MPS*04] Mortara M., Patanè G., Spagnuolo M., Falcidieno B., Rossignac J.: Plumber: A method for a multi-scale decomposition of 3d shapes into tubular primitives and bodies. In Proc. of ACM Solid Modeling and Applications (2004), pp. 339–344.
- [PGK02] Pauly M., Gross M., Kobbelt L. P.: Efficient simplification of point-sampled surfaces. In Proc. of the conference on Visualization (2002), pp. 163–170.
- [PKKG03] Pauly M., Keiser R., Kobbelt L. P., Gross M.: Shape modeling with point-sampled geometry. ACM Transactions on Graphics 22, 3 (2003), 641–650.
- [Pra87]
Pratt V.: Direct least-squares fitting of algebraic surfaces.
ACM Siggraph
21, 4 (1987), 145–152.
10.1145/37402.37420 Google Scholar
- [PSF04] Patanè G., Spagnuolo M., Falcidieno B.: Para-graph: Graph-based parameterization of triangle meshes with arbitrary genus. Computer Graphics Forum 23, 4 (2004), 783–797.
- [Sha06] Shamir A.: Segmentation and shape extraction of 3D boundary meshes. In Eurographics 2006 State of the Art Reports (2006), pp. 137–149.
- [SWK07] Schnabel R., Wahl R., Klein R.: Efficient RANSAC for point-cloud shape detection. Computer Graphics Forum 26, 2 (2007), 214–226.
- [VB04] Vanco M., Brunnett G.: Direct segmentation of algebraic models for reverse engineering. Computing 72, 1-2 (2004), 207–220.
- [VMC97] Várady T., Martin R. R., Cox J.: Reverse engineering of geometric models - an introduction. Computer-Aided Design 29, 4 (1997), 255–268.
- [WK04] Wu J., Kobbelt L.: Optimized sub-sampling of point sets for surface splatting. Computer Graphics Forum 23, 3 (2004), 643–652.
- [WK05] Wu J., Kobbelt L.: Structure recovery via hybrid variational surface approximation. Computer Graphics Forum 24, 3 (2005), 277–284.
- [YGZS05] Yamauchi H., Gumhold S., Zayer R., Seidel H.-P.: Mesh segmentation driven by gaussian curvature. The Visual Computer 21, 8-10 (2005), 659–668.
- [YLW06] Yan D., Liu Y., Wang W.: Quadric surface extraction by variational shape approximation. Lecture Notes in Computer Science 4077 (2006), 73.
- [YNBH06] Yamazaki I., Natarajan V., Bai Z., Hamann B.: Segmenting point sets. In Proc. of Shape Modeling and Applications (2006), pp. 4–13.
- [YQ07] Yang P., Qian X.: Direct computing of surface curvatures for point-set surfaces. In Symp. on Point-based Graphics (2007), pp. 605–608.
- [ZH04] Zhou Y., Huang Z.: Decomposing polygon meshes by means of critical points. In Multimedia Modeling Conference (2004), pp. 187–195.
- [ZMT05] Zhang E., Mischaikow K., Turk G.: Feature-based surface parameterization and texture mapping. ACM Transactions on Graphics 24, 1 (2005), 1–27.
- [ZTS02] Zuckerberger E., Tal A., Shlafman S.: Polyhedral surface decomposition with applications. Computers & Graphics 26, 5 (2002), 733–743.




