Using Human Resources Data to Predict Turnover of Community Mental Health Employees: Prediction and Interpretation of Machine Learning Methods
Funding: The study was supported by the National Institute of Mental Health R34 (NIMH R34MH119411).
ABSTRACT
This study used machine learning (ML) to predict mental health employees' turnover in the following 12 months using human resources data in a community mental health centre. The data contain 621 employees' information (e.g., demographics, job information and client information served by employees) hired between 2011 and 2021 (56.5% turned over during the study period). Six ML methods (i.e., logistic regression, elastic net, random forest [RF], gradient boosting machine [GBM], neural network and support vector machine) were used to predict turnover, along with graphical and statistical tools to interpret predictive relationship patterns and potential interactions. The result suggests that RF and GBM led to better prediction according to specificity, sensitivity and area under the curve (>0.8). The turnover predictors (e.g., past work years, work hours, wage, age, exempt status, educational degree, marital status and employee type) were identified, including those that may be unique to the mental health employee population (e.g., training hours and the proportion of clients with schizophrenia diagnosis). It also revealed nonlinear and nonmonotonic predictive relationships (e.g., wage and employee age), as well as interaction effects, such that past work years interact with other variables in turnover prediction. The study indicates that ML methods showed the predictability of mental health employee turnover using human resources data. The identified predictors and the nonlinear and interactive relationships shed light on developing new predictive models for turnover that warrant further investigations.
List of Abbreviations
-
- ALEs
-
- accumulated local effect plots
-
- AUC
-
- area under the receiver operating characteristic curve
-
- EN
-
- elastic net
-
- GBM
-
- gradient boosting machine
-
- HR
-
- human resources
-
- KNN
-
- K-nearest neighbour
-
- LR
-
- logistic regression
-
- ML
-
- machine learning
-
- NN
-
- neural network
-
- RF
-
- random forest
-
- SHARPs
-
- Shapley values
-
- SVM
-
- support vector machine
-
- VIMs
-
- variable importance scores
1 Introduction
Excessive employee turnover among mental health providers is a significant problem, with reported annual turnover rates ranging from 25% to 60% (Aarons and Sawitzky 2006; Beidas et al. 2016; Bukach et al. 2017). Some data indicate that over 70% of counties in the US report a severe shortage of mental health professionals (Hawkins 2021). This perpetuates a negative cycle of problems for remaining employees (e.g., increased workload and reduced morale). Predicting and preventing employee turnover is critical.
Turnover factors for mental health providers include low wages, high burnout, job dissatisfaction, low organisational support, lack of professional development opportunities (Cho and Song 2017) and concerns about workplace safety (Cho and Song 2017; Yanchus et al. 2015; Yanchus, Periard, and Osatuke 2017). Other factors include large client caseloads with severe symptoms (Hallett et al. 2024), increased job demands (Scanlan and Still 2013), staffing models (e.g., full-time vs. part-time; Beidas et al. 2016) and increased training demands for evidence-based practices (Brabson et al. 2019) in public mental healthcare systems. The combination of these individual and organisational factors contributes to increased turnover (SAMHSA, 2022). Although there are known turnover factors, as described above, the predictabilities are inconsistent across studies. Accordingly, effective turnover prevention strategies have yet to be identified.
Mental health organisations have struggled to identify high turnover risk employees and develop prevention strategies. The relevant challenges include the fact that turnover predictors in mental health literature are often identified through correlational analyses of turnover intention with limited variables collected from small survey samples. Although turnover intention correlates with actual turnover (Fukui, Wu, and Salyers 2019; Hom et al. 2017), their predictors can differ. For instance, turnover intention may be correlated with job stressors, while actual turnover could be associated with mental health provider characteristics, including age, work years in the field, educational degree and work hours (Fukui, Rollins, and Salyers 2020). Another challenge in survey methods with traditional analytical approaches (i.e., inferential statistics to test population parameters) is the limited application of the findings to local agencies, such as identifying high risk turnover cases in varying contexts (e.g., size of the agency, demographic composition and client populations). Finally, the traditional statistical methods (e.g., logistic regression) are limited in tailoring turnover prediction models based on the data characteristics, which often involve nonlinear, heterogeneous and interactive relationships. The present study aimed to overcome these limitations.
2 Background
In the current technological advancements enabling mental health researchers and practitioners to access and interpret big data, data-driven analytical approaches, including machine learning (ML), may identify localised turnover mechanisms. ML is a broad framework for extracting regularities from data using powerful automated algorithms (Hastie, Friedman, and Tibshirani 2001; Kassambara 2018). Unlike traditional statistical methods, ML is flexible in accommodating methods that can account for nonlinear and heterogeneous variable relationships. Although past turnover studies have utilised ML (Esmaieeli Sikaroudi, Ghousi, and Sikaroudi 2015; Sexton et al. 2005; Zhao et al. 2019), most of them were not focused on mental health service employees (who may differ from employees in for-profit firms), utilised a small set of ML methods or provided limited interpretations of the results (Fukui et al. 2023).
The primary goal of the current study was to apply various ML methods to predict community mental health employee turnover within the next 12 months using human resources (HR) data. Mental health employees are often overwhelmed by the amount of paperwork (Sullivan, Kondrat, and Floyd 2015), so collecting data through surveys may not always be ideal. On the other hand, HR data management systems contain useful variables that could predict turnover, yet they are often unutilised.
In the current study, we considered six representative ML methods to predict turnover versus nonturnover, including logistic regression (LR), elastic net (EN), random forest (RF), gradient boosting machine (GBM), neural network (NN) and support vector machine (SVM). Our focus is not only to examine the predictive power or accuracy of the variables in HR data but also to facilitate our understanding of turnover mechanisms by interpreting the relationships between turnover and the predictors using various graphical and statistical tools. Our study will promote the application of ML methods for turnover prediction in the mental health field. A comprehensive interpretation of the results will also shed light on developing future intervention strategies (e.g., Lundberg and Lee 2017; Molnar, Casalicchio, and Bischl 2020).
The rest of the article is organised as follows. First, we describe the data used in this study. Second, we briefly introduce the ML methods considered in the study, followed by several statistical and graphical tools to assist with result interpretation. We then present the results from the methods, including prediction power, identification of the most important predictors, visualisation of the patterns of the predictive relationships for the important predictors and exploration of potential interactions among the predictors (i.e., heterogeneous relationships). We conclude this article by discussing the main findings, limitations and potential directions for future research.
3 Method
3.1 Data
We used HR data from an urban community mental health centre in the US, which was obtained for the parent study to understand employee turnover mechanisms (NIMH R34MH119411). The HR data were extracted from five different data management systems by the HR, operations and clinical administration departments at the centre. The data were linked to one another by employee IDs, de-identified with research IDs, cleaned and processed for the ML applications by the researchers. Although the majority of data was well maintained in the data management systems, some data were incomplete. The missing data were filled in by HR staff where possible. The historical HR data (2011–2021) for the current study contained information on 621 employees. Among the 621 employees, 56.5% turned over (leavers) during the study period and 43.5% stayed (stayers). The Indiana University Institutional Review Board approved the original study. A waiver of informed consent was applied to the data already collected by the organisation.
We included 14 predictors from the HR data in our ML analyses. Six are categorical: gender (73% female vs. male), race (51% White vs. Black), educational degree (32% Associate degree and below, 34% Bachelors' degree and 34% Masters' degree and above), marital status (26% married vs. single), employee type (77% clinical vs. nonclinical) and exempt status (14% exempt vs. not exempt). Eight are continuous: employee's age, past work years, average hourly wage, average work hours per week, the total number of job training hours, the client information served by the employee (the proportions of male clients and clients with Schizophrenia diagnosis), and average client age. These data were all administratively collected in their routine HR data management. Table 1 shows the descriptive statistics of the included predictors by leavers and stayers.
| Predictors | Stayers (n = 270) | Leavers (n = 351) | ||||
|---|---|---|---|---|---|---|
| Mean | SD | Miss | Mean | SD | Miss | |
| Continuous | ||||||
| Age in the previous year | 44.2 | 13.1 | 0% | 40.4 | 12.6 | 0% |
| Past work years | 5.6 | 6.2 | 0% | 3.2 | 5.5 | 0% |
| Hourly wagea | 0.3 | 0.1 | 0.4% | 0.3 | 0.1 | 1.1% |
| Weekly work hours | 36 | 4.1 | 0.7% | 32 | 5.6 | 1.7% |
| Total number of job training hours | 120.6 | 112.5 | 7% | 103.1 | 84.6 | 8.5% |
| Average client age | 46.7 | 11.7 | 42% | 48.1 | 9.0 | 50% |
| % male clients | 58% | 24% | 42% | 59% | 23% | 50% |
| % clients with schizophrenia diagnosis | 49% | 32% | 42% | 55% | 31% | 50% |
| Frequency | Frequency | |
|---|---|---|
| Categorical | ||
| Gender | ||
| Female | 205 (75.9%) | 255 (72.7%) |
| Male | 61 (22.6%) | 95 (27.1%) |
| Miss | 4 (1.5%) | 1 (0.3%) |
| Race | ||
| Black | 146 (54.1%) | 163 (46.4%) |
| White | 121 (44.8%) | 171 (48.7%) |
| Miss | 3 (1.1%) | 17 (4.8%) |
| Educational degree | ||
| Associate degree and below | 87 (32.2%) | 111 (31.6%) |
| Bachelors' degree | 82 (30.4%) | 128 (36.5%) |
| Masters' degree and above | 101 (37.4%) | 112 (31.9%) |
| Marital status | ||
| Married | 81 (30%) | 87 (24.8%) |
| Single | 184 (68.1%) | 254 (72.4%) |
| Miss | 5 (1.9%) | 10 (2.8%) |
| Employee type | ||
| Clinical | 216 (80%) | 261 (74.4%) |
| Nonclinical | 54 (20%) | 49 (14%) |
| Miss | 0 (0%) | 41 (11.7%) |
| Exempt status | ||
| Exempt | 42 (15.6%) | 47 (13.4%) |
| Nonexempt | 228 (84.4%) | 304 (86.6%) |
- Note: The reference group for each categorical variable is in italics. Miss indicates missing data.
- a Hourly wage was log-transformed due to its non-normality and standardised by year to remove influence of inflation.
3.2 Data Preprocessing
Following the standard ML process, continuous predictors were standardised to ensure that their effects would not be influenced by their scale metrics (Hastie, Friedman, and Tibshirani 2001). In addition, because the wage ($) variable was highly skewed (skewness = 5.72, kurtosis = 52.49), we log-transformed it before the standardisation. All categorical data were dummy coded. There was a small amount of missing data on the predictors, ranging from 1% to 7%, except for the client-related variables (47%).
The missing data were imputed using the k-nearest neighbour (KNN) imputation, which is generally considered an effective and robust technique for imputing missing data (Jerez et al. 2010; Kuhn and Johnson 2013; Pereira, Basto, and Silva 2016; Troyanskaya et al. 2001). Simply speaking, KNN first identifies the complete cases similar to a missing case (based on Euclidian distance) and then takes a weighted average (weighted by the distance) of their observations to fill in the missing value (Troyanskaya et al. 2001). Because KNN is a nonparametric imputation method, it does not rely on any distributional assumptions nor assume linear relationships among the variables. Thus, it is unlikely to result in biased imputation or distort the relationships among the variables.
3.3 ML Methods
Below, we briefly introduce six ML methods used in the current study, focusing on conceptual understanding. The ML literature suggests that none of the methods could be universally superior. The relative performance can largely depend on the data set's characteristics (Domladovac 2021; Murugan, Nair, and Kumar 2019); thus, testing the competing methods in our particular study setting is important.
3.3.1 Logistic Regression (LR)
LR uses a logit link function to transform the probability of an event (i.e., turnover in the current study) and models the logit as a linear combination of a set of predictors. LR requires the logit to be correctly expressed as a linear combination of predictors. Any higher-order effects (such as interaction and quadratic effects), if considered, must be explicitly specified in the model. This requirement is not often satisfied in real-world applications. For simplicity or due to small sample sizes, researchers usually settle with a misspecified model, for example, a model with a small subset of possible higher-order effects (e.g., limited two-way interaction effects).
3.3.2 Elastic Net (EN)
EN is a regularisation technique that extends regular regression analysis by adding a penalty term (i.e., penalising the violated constraints) for regression coefficients in the discrepancy function for estimation. This penalty term will shrink the estimates, leading to biased estimates. However, this is intentionally designed to achieve a better variance-bias trade-off and improved generalisability. The penalty term makes EN capable of handling more nonlinear effects, even when the number of effects exceeds the sample size (Zou and Hastie 2005). In the current study, we fit several EN models with different complexities and chose the one that produced the highest area under a receiver operating characteristic curve, AUC (described below). These models included one with only first-order effects (i.e., no interactions, Model 1), one with all possible two-way interactions (Model 2), one with all quadratic effects for continuous predictors (Model 3), one that combined the effects in Models 2 and 3 (Model 4) and one with all two-way and three-way interactions (Model 5).
3.3.3 Neural Network (NN)
NN models relationships among the data by mimicking the learning process of the neurons in a human brain using a series of mathematical equations (Jun 2021). A simple NN involves an input layer (predictors) and an output layer (predicted outcome) connected by one or more hidden layers of nodes/neurons in the middle, which transfer the information from the input to the output. Predictors are combined through the hidden layer(s), and interactions are modelled implicitly, approximating any complex nonlinear relationships between the predictors and outcome (Hastie, Friedman, and Tibshirani 2001; Kavzoglu and Mather 2003). We only considered the simple NN in the current study.
3.3.4 Random Forest (RF)
RF is a powerful extension to the classification tree (a traditional nonparametric classification) method. The classification tree predicts an outcome by successively splitting the dataset into increasingly homogeneous subsets based on one predictor at a time (Breiman et al. 2017). Because a single classification tree is prone to biased and unstable results, compromising generalisability (Kirasich, Smith, and Sadler 2018; Strobl, Malley, and Tutz 2009), RF solves the problem by building many trees (e.g., 500). Specifically, it uses a resampling approach, such as bootstrapping, to create many samples from the original data and build a tree for each. It then assembles the results across all the trees to achieve more stable and accurate predictions. Furthermore, when building a tree, RF randomly selects a subset of predictors at each split. This reduces the correlations or redundancies among the trees, contributing to improved generalisability of the result (Breiman 2001; Kuhn and Johnson 2013).
3.3.5 Gradient Boosting Machine (GBM)
GBM offers another way to solve the generalisability problem of the classification tree. Like RF, GBM also builds a series of trees. However, it does so sequentially instead of parallelly by training each new tree to capture better the cases that have not been correctly classified (i.e., residuals) in the previous one. Briefly speaking, the first tree is grown based on the original dataset in which each observation is weighted equally. The second tree is then fit to a modified dataset with greater weights assigned to the cases that are difficult to classify and lower weights for those that are easy to classify (Zhang and Haghani 2015). This process continues for a specified number of iterations. The predictions from the multiple trees are then combined to determine the final classification prediction (Friedman 2002).
3.3.6 Support Vector Machine (SVM)
SVM involves searching for an optimal decision hyperplane (or decision boundary) to separate the classes in a categorical outcome (Brereton and Lloyd 2010). The decision hyperplane maximises the margin or distance between support vectors of the classes (leavers and stayers in our study). Support vectors are the closest data points to the hyperplane, making them the most difficult to classify. The basic idea is that if the most challenging cases can be optimally classified, so would the others. SVM allows for nonlinear decision boundaries, one major advantage over linear classifiers such as discriminant analysis (Gokcen and Peng 2002).
3.4 Cross-Validation
Overfitting (fitting random noise in a specific sample instead of true regularities in the corresponding population) is a common concern in ML methods. To prevent this problem, we used repeated K-fold cross-validation to evaluate the performance of the predictive models (Hastie, Friedman, and Tibshirani 2001). We set K = 10 based on the general practice and size of the data (James et al. 2021). This approach splits the data randomly into 10 equal-sized folds, and each fold is used as the testing data to evaluate the performance of the predictive model trained based on the other ninefolds. This process is repeated ten times, resulting in 100 sets of predictions. The predictions are then aggregated to evaluate the performance of each ML method according to the criteria described below.
3.5 Evaluation Criteria for Prediction Performance
Three criteria were used to evaluate the performance of the prediction models: specificity or true negative rate, sensitivity or true positive rate and area under the receiver operating characteristic curve (AUC). AUC is calculated based on sensitivity and specificity across various thresholds, providing an overall index of how well the cases are classified. An AUC value above 0.8 is generally considered good prediction power (Hosmer, Lemeshow, and Sturdivant 2013).
3.6 Interpretation of ML Results
As mentioned above, additional tools are needed to interpret the results from the examined ML methods. Several graphical and statistical tools were used in this study, including variable importance scores (VIMs), accumulated local effect plots (ALEs), Friedman's H-statistics and Shapley values (SHAPs). VIMs are used to capture the overall impact of each predictor. ALEs are graphical tools for visualising the marginal effects of the predictors. ALEs could also be used to visualise interaction effects. Given the many possible interaction effects (with 14 predictors, there could be 91 two-way interaction effects, not to mention higher-order interactions), we used H-statistics to identify a few impactful two-way interaction effects to investigate. Finally, SHAPs, case-wise statistics, were used for case studies to gain further insights into how leavers and stayers would be different in the potential predictors at the individual case level.
3.7 Variable Importance Scores (VIMs)
VIM is calculated for each predictor, providing a global measure of the impact of each predictor on the prediction (Kuhn 2022). The VIMs are often scaled to facilitate interpretation by dividing the original importance scores by the highest importance scores. Scaled importance scores range between 0% and 100%. For instance, an importance score of 60% means that the importance of the predictor is 60% of that of the most important predictor. There is no absolute criterion to evaluate the scaled importance scores. In practice, researchers often select predictors based on the rank orders of their importance scores (e.g., choose the top 10 scores depending on the number of predictors in the model, see Loh and Zhou 2021).
3.8 Accumulated Local Effect (ALE) Plots
ALEs can be applied to one or two predictors. For one predictor (e.g., X1), the ALE is a two-dimensional plot showing the marginal relationship between the predictor and a target outcome (e.g., the probability of turnover) averaged across the distributions of all other predictors (Friedman 2001; Molnar, Casalicchio, and Bischl 2020). In other words, it shows how the average prediction could change as a predictor changes. When applied to two predictors (e.g., X1 and X2), ALSs could display how the average prediction could change for different combinations of the two predictors across the marginal distributions of the other predictors (e.g., X3—Xp). Thus, they help visualise two-way interactions.
3.9 Identifying Potential Interaction Effects via Friedman's H-Statistics
Many ML methods (e.g., random forest) can account for potential interaction effects (heterogeneity) without explicitly expressing them in the models. In this case, it requires the use of indices such as Friedman's H-statistics to extract the potential interaction effects (Friedman and Popescu 2008). Briefly speaking, the H-statistics evaluates the degree to which a predictor (e.g., X1) may interact with any other predictors in the model. There are two types of H statistic values. One represents the proportion of the standard deviation (SD) in prediction from all predictors due to all interaction effects associated with a particular predictor. The other is more specific and can be used to evaluate the strength of a specific two-way interaction (e.g., between X1 and X2) relative to the joint impact from both predictors. For convenience, we call the former overall H and the latter specific H. For simplicity, we first used the overall H to identify a predictor for which the interaction effects could be most influential. We then focused on the predictor to explore its potential two-way interactions with any other predictors using the specific H. We used ALEs to portray the top 2 two-way interaction effects associated with the identified predictor.
3.10 Shapley Values (SHAPs)
SHAPs are case-wise statistics (i.e., available for each case), aiming to measure the contribution of each predictor to the prediction relative to the average prediction from all predictors for each individual (Rodríguez-Pérez and Bajorath 2020). SHAPs originate from a well-established coalitional game theory (Hart 1989) by treating predictors as players collaborating to produce the final prediction. As such, SHAPs have many desirable theoretical properties. For example, it provides a fair contribution allocation across the predictors and produces zero values for predictors that cannot predict (Lundberg and Lee 2017; Rodríguez-Pérez and Bajorath 2020). Given that SHAPs are case-wise, they are well suited for case studies which could facilitate our understanding of why a specific employee chose to leave while another decided to stay and what predictors were most influential to their decisions. We present the SHAPs for two extreme cases: one with the highest and one with the lowest probability of leaving.
3.11 Software Implementation
All analyses were conducted in R 4.2.1 (R Core Team 2021). Specifically, the caret package (Kuhn 2022) was used to implement the six ML methods with repeated 10-fold cross-validation and to obtain the variable importance scores. The iml package (Molnar 2018) was used to generate the ALE plots, H-statistics and SHAPs. The R scripts are in the online supplementary materials (https://osf.io/am9nj).
4 Result
4.1 Predictive Performance
AUC, sensitivity and specificity were used to evaluate the predictive performance of the methods. The average values for these criteria across 100 sets of prediction from the 10-fold repeated cross-validation are presented in Table 2. We used paired t-tests to examine whether the means for each criterion were significantly different for each pair of the methods (six methods, 15 pairs). To avoid inflated type I error rates, the α value for the t-tests was adjusted using the Bonferroni correction (i.e., corrected α = 0.05/15 = 0.0033) (Dunn 1961). Based on the significance of these tests, we ranked the methods for each criterion (the methods that did not differ significantly were grouped together). The rank orders were as follows. For AUC, (RF, GBM) > (LR, EN, NN, SVM); for sensitivity, (RF, GBM) > (NN, SVM) > (LR, EN); and for specificity, all methods had comparable performance (see Table 2).
| LR | EN | RF | GBM | NN | SVM | |
|---|---|---|---|---|---|---|
| Specificity | 0.73 (0.07) | 0.73 (0.08) | 0.73 (0.07) | 0.73 (0.07) | 0.72 (0.08) | 0.72 (0.07) |
| Sensitivity | 0.70 (0.08) | 0.71 (0.08) | 0.83 (0.07) | 0.80 (0.08) | 0.74 (0.09) | 0.73 (0.09) |
| AUC | 0.77 (0.04) | 0.77 (0.04) | 0.86 (0.04) | 0.84 (0.04) | 0.78 (0.05) | 0.78 (0.05) |
- Note: The highest values are in boldfaces for each evaluation criterion. Standard deviations across 100 cross-validation samples are shown in the paratheses. AUC standards for the area under the characteristic curve.
- Abbreviations: EN, elastic net; GBM, gradient boosting machine; LR, logistic regression; NN, neural network; RF, random forest; SVM, support vector machine.
4.2 Variable Importance Scores (VIMs)
We reported the top five predictors based on their VIMs (see Table 3). As shown in Table 3, past work years appeared to be the most important predictor across all methods. RF and GBM were highly consistent regarding their top five predictors, except for the fifth predictor (i.e., proportion of clients with schizophrenia diagnosis from RF vs. employee age from GBM). A few categorical predictors (i.e., exempt status, educational degree, marital status and employee type) appeared in the top five list from EN, NN or SVM. In total, Table 3 included 10 predictors, with past work years selected by all methods, average weekly work hours and the total training hours selected by four methods, employee age and proportion of clients with schizophrenia diagnosis selected by three methods, average hourly wage, exempt status and educational degree selected by two methods, and marital status and employee type chosen by one method.
| Rank | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Method | |||||
| LR | Past work years (100%) | Weekly work hours (64%) | Total training hours (51%) | Age (25%) | Proportion of clients with schizophrenia diagnosis (14%) |
| EN | Past work years (100%) | Total training hours (24%) | Weekly work hours (22%) | Exempt status (10%) | Educational degree (Masters' vs. Associate) (10%) |
| RF | Past work years (100%) | Total training hours (45%) | Weekly work hours (35%) | Hourly wage (28%) | Proportion of clients with schizophrenia diagnosis (24%) |
| GBM | Past work years (100%) | Weekly work hours (49%) | Total training hours (44%) | Hourly wage (32%) | Age (28%) |
| NN | Past work years (100%) | Exempt status (66%) | Total training hours (46%) | Educational degree (Bachelors' vs. Associate) (36%) | Marital Status (30%) |
| SVM | Past work years (100%) | Weekly work hours (51%) | Age (29%) | Proportion of clients with schizophrenia diagnosis (15%) | Employee type (11%) |
- Note: The scaled importance scores (in percent) are shown in the parentheses. AUC standards for area under the characteristic curve.
- Abbreviations: EN, elastic net; GBM, gradient boosting machine; LR, logistic regression; NN, neural network; RF, random forest; SVM, support vector machine.
4.3 Visualising Marginal Effects via ALEs
To visualise the marginal effects of the selected 10 predictors, we drew an ALE for each predictor in Table 3. If a predictor was included in the top five list of more than one method, we only presented the plot for the method with the highest AUC. For example, we presented the plot for exempt status based on NN instead of EN. More graphs can be found in the online supplementary materials (https://osf.io/am9nj). The ALEs for the 10 predictors are shown in Figure 1.
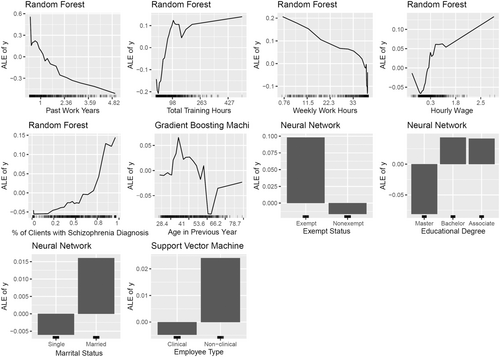
As shown in Figure 1, the predictive relationships appeared to be nonlinear. However, in general, higher total training hours and the proportion of clients with schizophrenia diagnosis were associated with a higher probability of turnover. On the other hand, more past work years and weekly work hours were associated with a lower probability of turnover. The predictive relationship for hourly wage appeared to be nonmonotonic (e.g., the direction of the relationship changed during the range of the predictor). Although a wage increase in the lower wage range could reduce the probability of turnover, it was associated with an increased probability of turnover in the higher wage range. A similar phenomenon occurred in the relationship between employee age and turnover. An increase in employee age was associated with an increased probability of turnover for younger employees (e.g., <35 years old) but a decreased probability for employees between 35 and 54 years old. Passing around 54 years old, the trend went up again. For the categorical predictors, those with exempt status, were married, held nonclinical positions or had masters' degree or above tended to have a higher predicted probability of turnover.
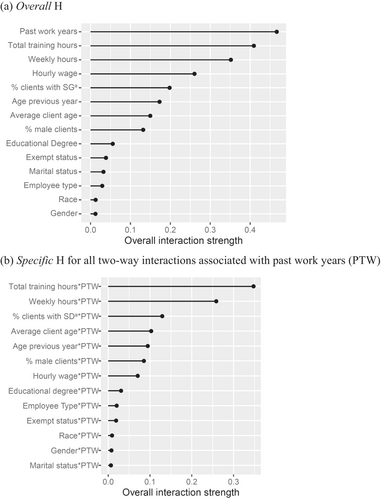
4.4 Interaction Effects
The ALEs in Figure 1 portray the marginal effects of the predictors but not interactions. Friedman's H-statistics (or H) were used to explore potential interaction effects. We only presented the H for the method that provided the best overall prediction (i.e., RF). Figure 2a displays the overall H for all the predictors. Recall that H values reflect the impact of all possible interaction effects associated with each predictor. The overall H was the highest (about 50%) for past work years, indicating that about 50% of SD in the prediction from all predictors was due to the interaction of past work years with one or more of the other variables. Centring on past work years, we examined all possible two-way interaction effects associated with it using specific H. As shown in Figure 2b, the top 2 two-way interaction effects are the one between past work years and total training hours (H = 37%) and the one between past work years and weekly work hours (H = 22%). These two interaction effects were visualised using ALEs in Figure 3.
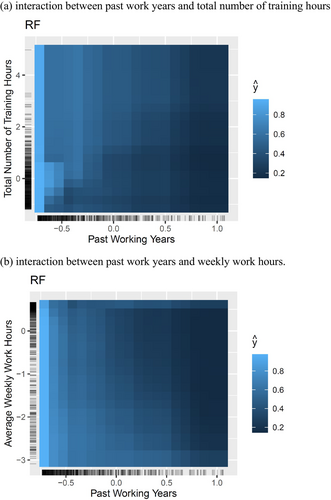
As shown in Figure 3, the ALEs for interaction are two-dimensional heatmaps with the x and y axis representing the two predictors that interacted with each other, respectively. The density of the colours reflected the level of predicted outcome for each combination of two predictor values, with lighter colours indicating a higher predicted probability of turnover. Figure 3 shows that newly hired employees are most likely to leave, and those who have worked for a long time are least likely to leave, regardless of the training or weekly work hours. In between, increased training hours could increase the probability of turnover (Figure 3a), while increased weekly work hours could decrease the probability of turnover (see Figure 3b).
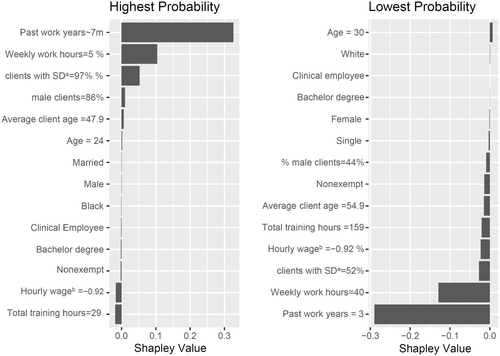
4.5 Case Study Using Shapley Values (SHAPs)
Finally, to examine how the leavers and stayers differ at the individual level, we extracted two extreme cases from the sample: a case with the highest probability to leave and a case with the lowest probability to leave. We compared their SHAPs of the predictors based on the RF results (see Figure 4). Note that the lengths of the bars in the figure reflect the magnitudes of the SHAPs, with a higher SHAP indicating a greater contribution of the corresponding predictor to the prediction for the specific case. One can see that the difference in prediction between the two cases was mainly determined by past work years, weekly work hours and the proportion of clients with schizophrenia diagnosis, generally consistent with the predictors' variable importance scores (i.e., VIMs). Taking a closer look at the characteristics of the two cases, we find that although both were clinical employees with nonexempt work status, the leaver case had shorter work history (7 months vs. 3 years), shorter work hours per week (5 vs. 40 h) and worked with more clients with schizophrenia diagnosis (97% vs. 52%). In addition, the leaver case was a younger black male versus an older white female; however, age, race and gender showed minimum influence (i.e., SHAPs) for these two sample cases.
5 Discussion
The current study used various ML methods to predict employee turnover in a community mental health centre using HR data. These ML methods had not been extensively tested for mental health employee turnover prediction, or practical interpretations of the results had not been offered in a way that can be intuitively translated for practitioners (e.g., leadership, HR) in mental health. Among the examined methods, the tree-based methods (i.e., RF and GBM) showed better predictive performance, followed by SVM and NN. LR and EN were generally inferior to the other methods, probably due to their limitations in accounting for complex nonlinear relationships among turnover factors (Holtom et al. 2008). The best-performing methods achieved >0.8 AUC, >0.8 sensitivity, and >0.7 specificity, indicating that the HR data were informative in predicting mental health employee turnover.
We presented the top five predictors from each method. As expected, there were overlaps and discrepancies. All methods agreed upon past work years being the most influential predictor. Total training hours and weekly work hours were also in the top three for most methods. These predictors could be more generalisable than the others. However, all the important predictors identified by the competing methods warrant further investigation and validation. For instance, three methods (i.e., LR, RF and SVM) identified that employees who worked with a higher proportion of clients with a schizophrenia diagnosis were more likely to leave. Working with more clients who struggle with severe mental health symptoms could add more job demands to the employees (leading to a higher probability of turnover). This concern has been discussed in the mental health literature (e.g., Rollins et al. 2010). However, the ML results provide the organisation's leaders and HR with direct implications for their turnover struggles in their organisational contexts.
Although some impactful predictors in this study were consistent with predictors discussed in the literature (e.g., past work years; Tsai, Bernacki, and Lucas 1989), others seemed to be inconsistent (e.g., no-significant associations found with exempt status, marital status, educational degree, Fukui, Rollins, and Salyers 2020). The differences in methods (e.g., traditional statistical methods vs. ML methods), data sources (e.g., survey data vs. HR data), tested variables and prediction models, and implementation settings could contribute to the discrepancies. Understanding these differences requires further investigation (e.g., interpreting the predictors in the local contexts).
We used ALEs to explore the marginal relationship of each important predictor with the turnover outcome. The plots revealed nonlinear or nonmonotonic relationships among predictors. For example, the predictability of employees' wages and age varied depending on their ranges, suggesting the need to examine their impacts in different career and life stages. Evidence for interaction effects also emerged according to H-statistics and ALE heatmaps. In particular, past work years were found to interact with other turnover predictors, meaning that the impact of turnover factors may depend on an employee's past work years. The length of work years is typically included in turnover prediction models as a covariate (to control for the effect). However, our study suggests the importance of considering it as a moderator (i.e., the interaction effects). For instance, the organisation's leaders should consider the impact of job factors (e.g., training) based on their employees' career stages instead of implementing uniform turnover prevention practices across employees. Furthermore, comparing and visualising the case (employee) characteristics with different turnover probabilities via SHAPs can also help communicate with the organisation's leaders and HR about the risk and preventive factors in their organizational contexts. These findings provide valuable insights on how to tailor the interventions, given varying employee characteristics.
The results from the current study support the dynamic processes (mechanisms) of turnover (e.g., nonlinear, nonmonotonic, moderator or mediator) suggested in turnover theories (Holtom et al. 2008). However, empirical evidence for the dynamic process was limited in the past due to the limitations of traditional statistical modelling, especially with small survey data or the challenge of collecting an actual turnover outcome. In this aspect, our study clearly demonstrated the advantages of ML.
5.1 Limitations and Future Directions
Some limitations of the current study are worth mentioning. First, the ML turnover prediction models were developed in the specific organisational contexts. ML is a data-driven approach that can localise the prediction model. However, this may limit the generalizability of the findings to other mental health settings or organisations. Second, the current sample size was on the small side in the ML literature (Zhao et al. 2019). Although the ML methods are applicable to similar sample sizes like ours (e.g., Quinn, Rycraft, and Schoech 2002; Tzeng, Hsieh, and Lin 2004; Zhao et al. 2019), small sample sizes could compromise the generalisability of the result. Future research is warranted to apply the ML methods to more extensive HR data across multiple mental health centres and to validate the result with external data sets. Third, the result is limited to the predictors included in the study. If more predictors are included, especially those with potentially high impact, then the predictive performance, the rank order of the variable importance score and the relationship patterns could change. Identifying important predictors that are missing in the current HR data and developing practical and efficient ways to integrate them into the HR data collection process would be promising in boosting the predictive power of HR data. Fourth, like other administratively collected data, HR data are not bias free. For instance, if particular subpopulations (e.g., gender, race and age) left the organisation systematically by other structural factors (e.g., insufficient organisational support or discrimination towards minoritised employees), prediction models trained by the historical data can be biased. Finally, the current study predicted turnover probability within the first year and considered only averaged effects across individuals. With more data, future research could be conducted to account for individual changes of turnover probability over time and examine time-varying and time-constant predictors for individual changes. This will require implementing ML methods that are capable of handling longitudinal categorical data with random effects (Cascarano et al. 2023).
6 Conclusion
The current study has significant implications for community mental health research. The study applied various ML methods to leverage routinely collected organisational data (e.g., HR data) for predicting employee turnover. It also provided extended insights on how to interpret the findings with various tools. Through the effort, our study revealed that the variable relationships among turnover predictors are more conditional, requiring the understanding of the interactive aspects than simply controlling for the effect of other variables (e.g., past work years). ML methods have advantages over traditional methods in this respect. Furthermore, our study suggests predictors that may be unique to the mental health employee population (e.g., the proportion of clients with schizophrenia diagnosis). This is an important first step to identifying high turnover risk employees for locally tailored and individualised (person-centred) interventions to prevent turnover in mental health.
7 Relevance for Clinical Practice
The proposed ML methods with HR data provide HR and leadership with a strategy to identify employees with high turnover probabilities without burdening them with additional data collection. Identifying such employees is a critical first step to developing localised (employee and agency-centred) interventions to prevent excessive turnover of the mental health workforce. The current study is a subset of the larger efforts (NIMH R34MH119411), which was initiated by collaborative efforts among mental health staff, organisational leaders and researchers to address high turnover struggles in the mental health field. Our next steps are for mental health practitioners and administrators to further contextualise the interpretations and applications in their specific organisational contexts through mixed methods approaches.
Author Contributions
Wei Wu and Sadaaki Fukui contributed to designing the study, analysing the data and drafting and approving the final manuscript.
Acknowledgements
We thank the study site's HR department and leadership for providing the data.
Disclosure
The material in this paper was first presented at the 2022 NIMH Mental Health Services Research Conference, August 2–3, 2022. The content is solely the responsibility of the authors and does not represent the official views of NIH.
Ethics Statement
The study was approved by the Indiana University Institutional Review Board (protocol#: 1908641462) and performed in accordance with the ethical standards as laid down in the 1964 Declaration of Helsinki and its later amendments, and waiver of informed consent was applied to the data already being collected by the organisation.
Conflicts of Interest
The authors declare no conflicts of interest.
Open Research
Data Availability Statement
Because of the sensitivity of data, the original data are not available to the public. However, a simulated dataset and the R scripts for all methods examined in the study as well as other online supplementary materials are available at https://osf.io/am9nj.




