Model parameterization to represent processes at unresolved scales and changing properties of evolving systems

1 INTRODUCTION

Simulation modeling is traditionally designed to examine interactions of systems components (Forrester, 1961). Nowadays, models have been widely used to predict and forecast states of ecological systems at individual sites, over regions and the globe (Bonan, 2019; Ciais et al., 2013). In this case, parameterization becomes equally important as model structure and external forcing to predict a state of an ecological system. Model structure determines general patterns of a system behavior, whereas parameter values represent properties of a specific system whose state at a given time and location is also influenced by external forcing (Luo et al., 2016; Figure 1).

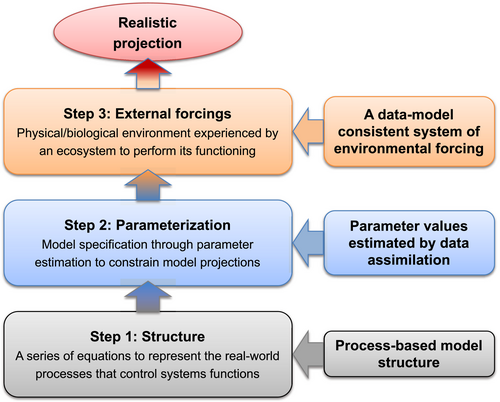
However, when simulation outputs do not match with observations, we mostly look into changing model structures but often ignore the roles of parameterization and forcing in determining a state of an ecosystem. While many of the model intercomparison projects often use common protocols as one method to control uncertainty arising from environmental forcing, how a model should be parameterized has not been carefully discussed in the literature. This paper first reviews a classic doctrine of parameters being constant, which is in contradiction with knowledge learned by modeling practitioners. Then, we will present two cases: processes at unresolved scales and changing properties of evolving systems, in which parameter values may have to change over time and space to represent system dynamics. Although this paper argues for spatiotemporally changing parameters, understanding how parameter values change still requires extensive research in the future.

2 ARE PARAMETERS CONSTANT OR VARYING?

Numerical values of parameters are usually considered constant, at least for the duration of computation of a single model run according to the seminal book on system dynamics (Forrester, 1961). This concept of constant parameter values may work very well for some physics systems, such as those based on fluid dynamics used in atmospheric sciences. Models of fluid dynamics represent natural systems through fundamental, physical equations that do rely on constant parameter values, such as gravity. In comparison, ecosystem models rarely can draw upon such fundamental equations, but rather rely on empirical relationships and approximations to describe interactions among system components. However, the issue of how well this concept of parameters being constant can be applied to ecosystem modeling has not been examined.

Almost all the text books of biological and ecological modeling define parameters to be constant (Bonan, 2019; Haefner, 1996). The concept of constant parameters has been prevailing and thus becomes a classic doctrine from the birth of simulation modeling. As a consequence, most ecosystem models set parameter values to be constant over time and space. With constant parameters, spatial and temporal variations in modeled system behaviors are expected to be fully represented by environmental scalars. For example, photosynthetic capacity, which represents a property of a photosynthesis system and usually is represented by carboxylation capacity, is set to be a constant in many models (Rogers et al., 2017). Another example is the baseline decomposition rates of litter and soil organic matter that are set constants (Lawrence et al., 2020). The litter decomposition rate is usually derived from litter decomposition studies and often inappropriately called decay constant in the literature (i.e., a misnomer; Zhang, Hui, Luo, & Zhou, 2008). Changing decomposition rates over time and space are expected to be represented by temperature, moisture and other scalars in models.

However, when we apply a model that was well calibrated for its parameters at one site to another site for simulation, we usually have to recalibrate parameters in order to fit observations well at the other site (Weng & Luo, 2011). This issue of parameter recalibration is commonly known among modelers who apply their models to different sites but may rarely occur to those modelers who only use models for simulation and prediction without much data–model comparison. This recalibration (or tuning, as commonly called among model practitioners) practically changes parameter values from one site to another site and thus makes parameters not necessarily constants as often taught by traditional simulation modeling books. This concept of varying parameters is also implicitly acknowledged when different vegetation types have different parameter values in global land models (Lawrence et al., 2020). When dynamic vegetation has been incorporated into a model, many parameters, such as coefficients of plant allocation and litter decomposition, all vary with time as vegetation changes (Weng et al., 2015).

To better parameterize photosynthesis models, Medlyn et al. (1999) examined variability in model parameters from 19 gas exchange studies on tree and crop species. Values of two key parameters, the maximum rate of Rubisco activity, and the potential rate of electron transport at a reference temperature of 25°C, vary considerably among species, particularly between crop and tree species. Their results suggest that alternative parameter values are required for modeling photosynthesis of different plant types. Other reviews and syntheses have also shown that model parameters and plant traits often change with time, vary across sites of measurements, and are better represented as probability distributions (Kattge et al., 2011; Lebauer, Wang, Ritcher, Davidson, & Dietze, 2013; Saugier, Roy, & Mooney, 2001).

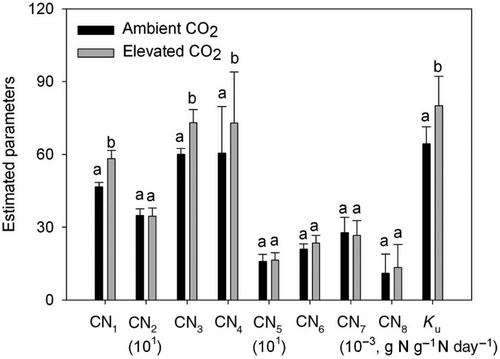
Data assimilation, a statistically rigorous method to estimate parameter values, not only can better calibrate models against data but also offers great opportunities to understand model parameterization. When data assimilation is applied to integrate data from global change experiments with models, two or more sets of parameters are estimated, each at one treatment level (Luo et al., 2003). Comparison of posterior probability density functions shows that estimated carbon turnovers in foliage and fine root pools are much higher at elevated than ambient CO₂ at the Duke forest CO₂ enrichment experimental site (Luo et al., 2003; Xu, White, Hui, & Luo, 2006). Elevated CO₂ alters parameters values for C:N ratios in foliage, fine roots and litter; plant N uptake; and carbon exit rates (i.e., inverse of C residence times) in foliage, fine root, woody biomass, structural litter, and passive soil organic matter in a carbon–nitrogen coupled model (Figure 2; Shi, Yang, et al., 2015). Experimental warming also alters model parameters. For example, the 9 year warming treatment in a tallgrass prairie in Great Plains of USA decreases allocation of gross primary production to shoot, and turnover rates of both shoot and root carbon pools but increases the turnover rates of litter and fast soil carbon pools (Shi, Xu, et al., 2015). Experimental warming in Alaska tundra significantly changes three out of the 16 parameters: light use efficiency (LUE), baseline (i.e., environment-corrected) turnover rates of the fast and slow soil organic carbon (SOC) pools (Liang et al., 2018). When different sets of parameter values are used in model predictions, predicted carbon sequestration in terrestrial ecosystems is substantially different in response to global change (Liang et al., 2018; Xu et al., 2006).

Parameter values not only vary with treatments in global change experiments but also across space. Data at 12 eddy-covariance towers across continental USA were used to estimate parameters of a flux-based ecosystem model (Li et al., 2016). Estimated parameters have different degrees of variation across sites. The estimated parameters related to stomatal conductance exhibit high cross-site variation while the ratio of internal to air CO₂ concentration and canopy light extinction coefficient vary little among these sites. Variations of some parameters (e.g., activation energy of carboxylation, temperature sensitivity of respiration, and stomatal conductance coefficient) are highly correlated with environmental conditions. In another study, 25,444 vertical soil profiles in US continent are assimilated into Community Land Model (CLM) version 5 (Tao et al., submitted ). Optimally estimated parameters that are kept constant across the whole continent explain for 36% variation in the observed SOC content. When a deep learning method is applied to estimate spatially heterogenous parameter values, the optimized model can explain for 62% variation in the observed SOC content. Data assimilation of both eddy-flux data and soil carbon profile data indicates that parameter values vary over space in order to match data well.

Many other studies have also indicated that the predictive skills of models have been greatly improved if parameter values are linked to climate, vegetation, and edaphic properties. For example, the maximum rate of Rubisco activity varies with mean climate (Smith et al., 2019), leaf chlorophyll content (Luo et al., 2018), and leaf nitrogen (Walker et al., 2017). Similarly, global variation in inherent water use efficiency is significantly correlated with mean precipitation (Franks et al., 2018).

No matter which models or what data sets are used, all the data assimilation studies suggest that some of the optimally estimated parameters vary over space, with time, at different treatments of global change experiments, and across vegetation types, whereas other estimated parameters change little. It is not understood whether the degree of parameter variations over time and space is related to model structures, differences in data sets used, or inherent properties of parameters themselves. Nevertheless, it is very clear that the differences in estimated parameters can propagate through models, leading to differences in model predictions.

3 PROCESSES AT RESOLVED VERSUS UNRESOLVED SCALES FOR A MODEL

Parameter variation is partly due to processes at unresolved scales of model. A model is an abstraction of real-world processes. Those processes that are explicitly described in a model are considered processes at resolved scales. Those processes at the resolved scales for a given model are often influenced by many processes that are not explicitly described in the model (i.e., processes at unresolved scales). For example, classic soil carbon dynamics models, such as CENTURY or RothC, explicitly represent decomposition of SOC in multiple pools (Coleman & Jenkinson, 1996; Parton, Stewart, & Cole, 1988). The decomposition process is influenced by many processes and factors, such as environmental variables, litter quality, organomineral properties of SOC, microbial attributes, soil erosion, mineralogy topography, land management, land use change, and other disturbances (Doetterl et al., 2015; Dümig, Smittenberg, & Kögel-Knabner, 2011; Egli et al., 2008; Sistla & Schimel, 2013) (Figure 3). Environmental variables alone that influence SOC decomposition could include temperature, moisture, oxygen, and acidity, all varying with soil profile, space, and time. None of the models can explicitly include all those processes and factors. Most soil models have explicitly incorporated influences of temperature, moisture, litter quality, and soil clay content on decomposition of soil organic matters (Parton et al., 1988). But many other processes and factors, such as soil acidity and physiochemical binding, are not explicitly resolved in the models. Those processes at unresolved scales can potentially interact with the processes at resolved scales to influence soil carbon dynamics.

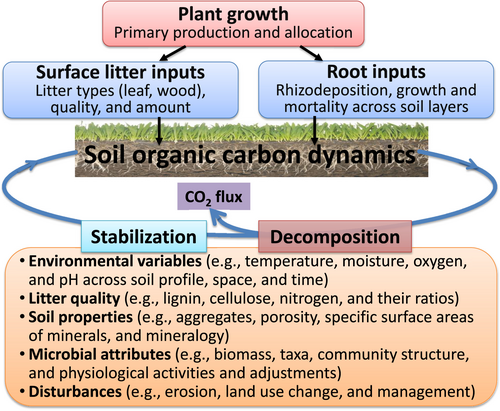
One attempt to deal with processes at unresolved scales is to add more processes into models as the modeling community tends to do at present. For example, major efforts have been made to explicitly represent microbes in Earth system models (Allison, Wallenstein, & Bradford, 2010; Wang, Post, & Mayes, 2013; Wieder, Bonan, & Allison, 2013). Many microbial processes, such as enzymatic depolymerization, microbial dormancy, and microbial functional groups, have been incorporated into a variety of microbial models (Sulman et al., 2018). No matter how many microbial processes are incorporated into models, there are still lots more that cannot be included (note that discussion on what are the criteria for including or not including a process in one model is beyond the scope of this paper). There are always processes at unresolved scales that potentially interact with processes at resolved scales to influence model results. Thus, it is essential to vary parameter values to represent the interactions of processes at unresolved scales with processes at the resolved scales as commonly practiced in atmosphere modeling (Bauer, Thorpe, & Brunet, 2015).

The notion of using varying parameters to represent processes at unresolved scales can be further illustrated from both experimental and modeling studies in an Alaska permafrost ecosystem. A field experimental warming has been conducted in upland moist acidic tundra in the Eight Mile Lake Watershed, Alaska, USA, since 2009 (Natali et al., 2011). Experimental warming is implemented with six snow fences to accumulate snow that insulates the ground so as to increase surface and deep soil temperatures during the winter. The experimental warming has induced a suite of changes in aboveground biomass (Deane-Coe et al., 2015; Salmon et al., 2016), nitrogen availability (Salmon et al., 2016), vegetation phenology (Natali, Schuur, & Rubin, 2012), gaseous carbon fluxes (Mauritz et al., 2017; Natali, Schuur, Webb, Pries, & Crummer, 2014), and microbial attributes (Xue et al., 2016).

When two versions of CLM (CLM4.5 and 5.0) are applied to the field experiment, predicted gross primary productivity (GPP), ecosystem respiration (R_eco), and net ecosystem C exchange (NEE) linearly increase with warming over 8 years from 2009 to 2016 (Schädel et al., 2018). In contrast, the field observation showed initial increases in growing season GPP, R_eco, and NEE in response to warming-induced permafrost thaw, resulting in a higher carbon sink capacity in the first 5 years, followed by a strong carbon source in years 6–8. Field observations and model simulations showed similar increasing trends in soil temperatures and thaw depths with warming. However, warming effects on water table depth differ between the field observations and model simulations; warming created wetter soils in the field and drier soils in the models. The divergence of model results from field experiments was attributed by authors of that modeling study to structural deficiency of the models to predict complex ecosystem responses, such as subsidence, hydrology, and nutrient cycling, to experimental warming (Schädel et al., 2018).

Community Land Model 4.5 and 5.0 are among the most comprehensive models. Those two versions of CLM have incorporated enough processes to simulate subsidence, hydrological changes, and nutrient dynamics in response to experimental warming. For example, warming-induced subsidence can be simulated by varying thickness of soil layers in the multilayer model. Changes in soil moisture and water table in association with warming-induced subsidence can be simulated by varying the field water holding capacity and water table depth. In other words, observed subsidence and its associated changes in hydrology, nutrient cycling, and carbon processes in response to experimental warming can be well represented by varying parameters instead of adding more processes in the already complex model.

Indeed, varying parameters is another modeling approach that acknowledges the notion that a model needs not explicitly incorporate all processes at resolved scales. Rather, parameter values are to vary for a given model structure to represent interactions of processes at unresolved scales with those processes explicitly modeled as long as the model adequately incorporates major processes. For example, warming-induced soil subsidence is largely due to melting of excess ice within the soil that causes the soil surface to collapse and subside with warming. It may not be necessary to explicitly simulate the process of ice melting in the model. Instead, we can vary the parameters related to thickness of soil layers to represent subsidence if our research objective is to simulate the carbon cycle reasonably well.

To represent observations from the warming experiment at the Eight Mile Lake, Alaska, Liang et al. (2018) assimilated six data sets into Terrestrial ECOsystem (TECO) model to optimally estimate 16 parameters. The TECO model uses multiple soil layers to track dynamics of thawed soil under different warming treatments. Results of data assimilation indicate that experimental warming increased LUE of vegetation photosynthesis but decreased baseline (i.e., environment-corrected) turnover rates of SOC in both the fast and slow pools in comparison with those under control. The warming-induced changes in baseline turnover rates of fast and slow SOC may reflect changes in microbial community composition and activity, which has been observed to change in response to warming and permafrost thaw in Arctic ecosystems (Hale et al., 2019; Johnston et al., 2019; Xue et al., 2016). These microbial changes likely are the mechanisms underlying the altered SOC turnover rates but have not been explicitly represented in the TECO or many other models. Those microbial changes at unresolved scales for the TECO model are implicitly represented by changes in parameter values before we develop the capability to explicitly represent them at resolved scales. Similarly, the estimated changes in LUE under the warming treatment also represent many processes at unresolved scales of the TECO model.

4 CHANGING PROPERTIES OF EVOLVING SYSTEMS

Parameters being not constant partially roots in the fact that ecological systems are always evolving in the real world. Almost all ecological processes, either at resolved or unresolved scales for a given model, are evolving over time, leading to changing properties of ecological systems (i.e., time-dependent or time-varying properties). There are ample examples to show that properties of ecological systems commonly vary with time and space. For example, the optimal temperature at which photosynthesis is maximized is a property of photosynthetic systems. This property has been documented to ubiquitously vary at leaf, plant, and ecosystem scales as temperature changes through photosynthetic acclimation and adaptation (Berry & Bjorkman, 1980; Huang et al., 2019; Mooney, Björkman, & Collatz, 1978; Niu et al., 2012). Data synthesis from 169 globally distributed sites of eddy covariance shows that the optimum temperature of net ecosystem exchange is positively correlated with annual mean temperature over years and across sites (Niu et al., 2012). Shifts of the optimum temperature of net ecosystem exchange are mostly due to temperature acclimation of GPP. The optimum temperature for ecosystem-level GPP, however, is consistently lower than the physiological optimal temperature of leaf-level photosynthesis (Huang et al., 2019).

Acclimation and adaption of plant and soil respiration have also been widely observed (Atkin, Holly, & Ball, 2000; Luo, Wan, Hui, & Wallace, 2001). Changes in the temperature sensitivity of root respiration, or Q₁₀ values, differ between and within plant species, partly due to temperature-dependent changes in adenylate control and substrate supply (Atkin et al., 2000). Field experiments also show that temperature sensitivity of soil respiration declines in response to warming treatments (Luo et al., 2001; Melillo et al., 2002). The acclimation in temperature sensitivity of soil respiration may be due to several mechanisms, such as plant carbon supply, altered root and microbial activity, and substrate limitation. Water table has been found to change over time and with warming treatments at the Eight Mile Lake (Mauritz et al., 2017). Water table is a very important property that influences many processes of Alaska tundra ecosystems.

Much effort has been made to incorporate the time-varying properties of ecological systems into models. For example, plant photosynthetic and respiratory acclimation to temperature has been integrated into an ecosystem model (Friend, 2010). This model allows the optimum temperature for electron transport to respond to changes in plant growth temperature by assuming that the optimum leaf temperature linearly decays toward an equilibrium temperature. CLM4.5 incorporates representations of photosynthetic and leaf respiratory temperature acclimation by linking various parameters, such as maximum rate of carboxylation, maximum potential rate of electron transport, dark respiration, and CO₂ compensation point, to leaf temperature (Lombardozzi, Bonan, Smith, Dukes, & Fisher, 2015). Other studies have also incorporated plant photosynthetic and/or respiratory acclimation into land biogeochemical models (Arneth, Mercado, Kattge, & Booth, 2012; Atkin et al., 2008; Ziehn, Kattge, Knorr, & Scholze, 2011). Those studies fundamentally use model parameterization to account for acclimation of photosynthesis and respiration as suggested from empirical evidence (Atkin et al., 2008; Kattge & Knorr, 2007).

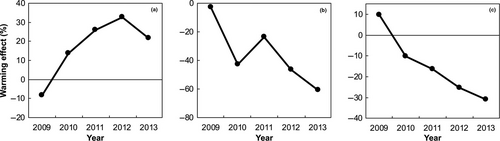
Parameters can also be directly estimated from site-specific data to represent changing properties of a given ecosystem. When six data sets in each year were assimilated to TECO model to estimate yearly values of its parameters, changes in those parameters varied with treatment years (Figure 4). The warming effect on LUE gradually increases over the 5 years since the experiment starts (Figure 4a). In contrast, the baseline turnover rates of the fast and slow SOC pools decrease with amplifying magnitudes over time (Figure 4b,c). With changing parameter values over time, the TECO model predictions match with observations much better than that with fixed parameter values. The dependence of parameter changes on treatment time suggests that warming-induced changes in ecosystem properties are gradual as exposure time to environmental stimuli can affect the extent to which acclimation occurs (Smith & Dukes, 2013). This site-specific parameterization is not only essential for forecasting ecosystem state changes under experimental treatments but also contributes to our general understanding of parameter variation, especially when parameters are estimated from many experiments.

5 CONCLUDING REMARKS

Model parameterization plays an equally important role as do model structure and environmental forcings in predicting the state of an ecological system. When prediction of a model does not match with observations well, it may not be productive to look only at model structure and ignore parameterization and forcing. Parameter tuning is a common practice for simulation modeling and, unfortunately, is a skeleton in closet for modelers for several decades. Tuning parameter values is one of the most tedious and laborious work, but we did not learn much from it as no way to record the process of tuning until parameters can be rigorously estimated from a statistically rigorous method—data assimilation.

Limited studies on model parameterization using data assimilation and other methods have shown that parameter values need to vary over space, with time, at different treatments of global change experiments, and across vegetation types in order to fit model predictions well with observations. Although there is ample empirical evidence that properties of ecological systems, which parameters are supposed to represent, vary with time and space, we have very limited understanding on which, how, how much, and why parameters vary. Some of the parameters that represent changing properties of ecological systems, such as photosynthetic capacity, optimal temperature of photosynthesis, and temperature sensitivities of plant and soil respiration, should be changing, regardless of model structures, in order to fit observations well. Changes in some other parameters may depend on model structure. For example, stomata conductance is represented in different ways in different models. Estimated parameter values from the same data sets are likely different with different stomata model structures. Moreover, estimated parameter values from data assimilation are surely conditional upon data availability. In the future, we need to conduct extensive research to understand how much and why parameters vary over space and time; what are the patterns, the causes or mechanisms underlying parameter variations; and how data availability and model structure influence changes in parameters.