Testing for independence in 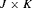contingency tables with complex sample survey data

The test of independence of row and column variables in a 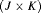contingency table is a widely used statistical test in many areas of application. For complex survey samples, use of the standard Pearson chi-squared test is inappropriate due to correlation among units within the same cluster. Rao and Scott (1981, Journal of the American Statistical Association 76, 221–230) proposed an approach in which the standard Pearson chi-squared statistic is multiplied by a design effect to adjust for the complex survey design. Unfortunately, this test fails to exist when one of the observed cell counts equals zero. Even with the large samples typical of many complex surveys, zero cell counts can occur for rare events, small domains, or contingency tables with a large number of cells. Here, we propose Wald and score test statistics for independence based on weighted least squares estimating equations. In contrast to the Rao–Scott test statistic, the proposed Wald and score test statistics always exist. In simulations, the score test is found to perform best with respect to type I error. The proposed method is motivated by, and applied to, post surgical complications data from the United States’ Nationwide Inpatient Sample (NIS) complex survey of hospitals in 2008.