Genomic evaluation using SNP- and haplotype-based genomic relationship matrices in a closed line of Duroc pigs
Abstract
A simulation analysis and real phenotype analysis were performed to evaluate the impact of three different relationship matrices on heritability estimation and prediction accuracy in a closed-line breeding of Duroc pigs. The numerator relationship matrix (NRM), single nucleotide polymorphism (SNP)-based genomic relationship matrix (GRM) (GS), and haplotype-based GRM (GH) were applied in this study. We used PorcineSNP60 genotype array data (38 114 SNPs) of 831 Duroc pigs with four selection traits. In both heritability estimation and prediction accuracy, the accuracy depended on the number of animals with records. For heritability estimation, a large difference in the results among three relationship matrices was not shown, but the trend of the estimated heritabilities between GRMs, that is GS < GH, was shown in this population. For the accuracy of prediction values in test animals, the accuracies of prediction values obtained by two GRMs were higher than that by the NRM in this population. The accuracies obtained by GRMs using animals with no records were lower than that by the NRM using animals with their performance records, but were close to that by the NRM using animals with full-sib testing records.
Introduction
In Japan, some local animal research stations have performed closed-line breeding based on estimated breeding values (EBVs) predicted by best linear unbiased prediction (BLUP) in purebred pigs (Suzuki et al. 2005; Kadowaki et al. 2012). In pig closed-line breeding, the average population size of each generation is relatively small (about 10–20 sires and about 30–50 dams). To increase the accuracy of EBVs, it is necessary to utilize pigs with records obtained through performance tests or by full-sib testing in the analysis. However, obtaining animals with these records available is time-consuming and costly. Recently, high-density single nucleotide polymorphism (SNP) arrays have become available for pigs (Ramos et al. 2009), and genomic evaluation using SNP arrays could be effective in pig closed-line breeding when animals with performance or full-sib testing records are not available.
Using the BLUP method, EBVs are predicted using the numerator relationship matrix (NRM) based on pedigree relationships. The coefficients of the NRM are the expected genetic relationships among animals in the population. For example, a coefficient of the NRM between animals equals 0.5 when two full-sibs are from unrelated parents. In genomic evaluation, the genomic best linear unbiased prediction (GBLUP) method is one of the approaches for predicting the genomic estimated breeding value (GEBV). In GBLUP methods, a SNP-based genomic relationship matrix (GRM) is commonly used (VanRaden 2008), and the genetic relationship among animals is based on the actual Mendelian segregation at the genome level. Consequently, the SNP-based GRM can measure genetic relationships more accurately than the NRM. However, the problem is that SNPs in the SNP array are usually not quantitative trait loci (QTL), because the SNPs in the array are selected based on their high levels of polymorphisms in multi-pig breeds (Ramos et al. 2009). Thus, genomic evaluation using a SNP-based GRM might not be an effective method. Comparatively, genomic evaluation using ancestral haplotypes may be more effective than those using SNPs, if reliable ancestral haplotypes are obtained and the ancestral haplotypes have greater linkage disequilibrium (LD) with QTL than SNPs in the SNP array. Reliable ancestral haplotypes can be obtained in a closed-line breeding population, because the segregation of alleles can be traced using a known pedigree and thus the recombination of haplotypes can be detected. Therefore, the impact of these different relationship matrices on genomic evaluation must be analyzed in a closed-line breeding population.
The objective of our study is to evaluate the impact of three different relationship matrices (NRM, SNP-based GRM and haplotype-based GRM) on heritability estimation and the prediction accuracy of the EBV and GEBV ((G)EBV) in closed-line breeding of Duroc pigs by simulation analysis and real phenotype analysis. We used real genotype data of a Duroc purebred population comprising a seven-generation pedigree in the simulation analysis, and these genotypes and four selection traits were used in the real phenotype analysis.
Materials and Methods
Experimental animals, phenotypes and genotyping
Genotypes, phenotypes and pedigree information for this study were obtained from previously published data by a genome-wide association study (GWAS) (Sato et al. 2016). All procedures involving animals followed the Guidelines for the Care and Use of Laboratory Animals established by the National Livestock Breeding Center. Complete descriptions of the experimental population, phenotypes and SNP information were reported previously by Sato et al. (2016). In short, a total of 836 Duroc purebred pigs were used in this study. These pigs were based on one family comprising the first to the seventh generation. Sixteen boars and 22 gilts were mated in the first generation, and 22 gilts from among their offspring and nine boars were then mated in the second generation. Pigs in the first and second generations were regarded as the base population, and closed-line breeding was then performed from the third to the seventh generation. This population was selected on the basis of average daily gain from 30 to 105 kg of body weight (DG), ultrasonically measured loin eye muscle area (LEA), backfat thickness at a weight of 105 kg (BF), and intramuscular fat content (IMF). DG, LEA and BF were recorded in all animals, and IMF was recorded in sib-tested animals. These four phenotypes were used in the real phenotype analysis.
Genomic DNA from 836 animals was genotyped using the Illumina PorcineSNP60 BeadChip (Illumina, San Diego, CA, USA) according to manufacturer protocols. Image data were analyzed with iScan (Illumina) and genotype data were then called using the genotyping module contained in the GenomeStudio software (Illumina). Autosomal chromosomes were used and SNP quality control was assessed using PLINK software (Purcell et al. 2007). The exclusion criteria for SNPs were minor allele frequency (MAF) < 0.01, call rate < 0.95, and a Hardy–Weinberg equilibrium test with P-value < 0.001. The exclusion criteria for animals was a call rate < 0.95. Following quality control measures, the final data set included 831 animals with 38 114 SNPs, and was available for this study.
Simulations
In order to generate the true breeding value (TBV) and phenotype, we used real genotype data and pedigree information from the Duroc pigs in a simulation analysis. We assumed two different QTL genotypes (SNP-QTL and Haplotype-QTL), and then generated TBVs as follows.
SNP-QTL: the SNPs in the SNP array were assumed to be candidate QTL, meaning that QTL were in perfect LD with SNPs for genomic evaluation (i.e. some SNPs were QTL). Missing genotypes were imputed by DualPHASE (Druet & Georges 2010) and were used to generate QTL effects. A total of 500 SNPs in the MAF range (0.10 ≤ MAF ≤ 0.50) were randomly selected from the SNPs on the SNP array and were defined as the QTL. The TBV of an animal was obtained as a sum of all true QTL genotypic values, that is,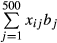 
, where xij is the genotype for the j-th QTL of the i-th animal (coded as −1, 0 or 1 for the homozygote, heterozygote and the other homozygote, respectively) and bj is the allele substitution effect of the j-th QTL. The allele substitution effect was generated from a gamma distribution with a shape parameter of 0.4 and scale parameter of 1.66 (Meuwissen et al. 2001), and the signs of the allele substitution effect were randomly selected.
Haplotype-QTL: the haplotype loci were assumed to be candidate QTL, and this means that QTL were not in LD with SNPs for genomic evaluation (i.e. SNPs were not QTL, but were in some extent of LD with QTL in this population). The QTL effect was generated as follows: first, ancestral haplotypes, which are a mosaic of haplotypes from different physical ancestors, were constructed from all SNPs on the SNP array using DualPHASE (Druet & Georges 2010) in each animal's chromosome. The number of ancestral haplotype states was assumed to be 20. Second, a total of 500 loci were randomly selected from all loci and were defined as the QTL. Third, haplotypes were randomly selected from all ancestral haplotypes at each locus. Then, the selected haplotypes were assumed to be QTL allele 1 and the others were assumed to be QTL allele 2, if the sum of the MAFs of the selected haplotypes were between the range of 0.10 and 0.50. After obtaining QTL alleles in 500 loci, these QTL genotypes could be regarded as SNP genotypes, and the calculation of TBVs was performed using the same method as the SNP-QTL scenario. The LD value (r2) was calculated to evaluate the extent of LD between QTL and SNPs on the selected loci. The mean and standard deviation (SD) of r2 were 0.06 and 0.14, respectively, and the proportion of QTL with r2 > 0.20 was 0.084.
After obtaining TBVs for each simulated QTL effect, phenotypes were generated by scaling the residual variance relative to the variance of the TBVs of individuals in the base generation of the pedigree. The variance of the TBVs (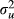
) was given by u'u/(n − 1), where u is a vector of TBVs of animals in the base generation, and n is the number of animals in that generation. The heritability of the phenotype (h2) was set at 0.50, and phenotypic variance was assumed to be 100. The variance of the TBVs was adjusted to 100 × h2, and the residual value of an animal was generated from 
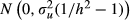. The phenotype was simulated by adding the TBV and the residual value, and 100 replicates were simulated in two different QTL genotypes.
Statistical analysis
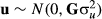and residual effect with 
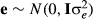, respectively. b represents total mean in the simulated phenotype data, and represents total mean, sex (three classes; boar, barrow and gilt), and generation (seven classes) effects in the real phenotype data. 
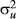and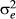 
represent additive genetic variance and residual variance, respectively, and I is the identity matrix. G is a relationship matrix, and we used three different relationship matrices as an NRM, SNP-based GRM and haplotype-based GRM. Two GRMs were defined as follows.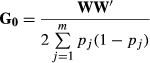
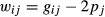
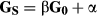
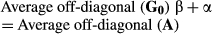
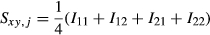
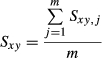
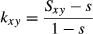
Heritability estimation and prediction accuracy
Heritability was estimated and the accuracies of (G)EBV were assessed in simulated and real phenotype data using the ASREML 3.0 program (Gilmour et al. 2009). For heritability estimation in the simulation study, the mean and standard deviation (SD) of 100 replicates were calculated for the combinations of different QTL effects (two analyses), animal groups (two analyses) and relationship matrices (three analyses). In the real phenotype analysis, phenotypes of all animals with records were used.
For prediction accuracy, the genetic and residual variances were fixed to predict the (G)EBV for comparing the accuracy of the (G)EBV among three relationship matrices in each analysis. The (G)EBV was predicted by using the setting variances in the simulation analysis and the estimated variances by the NRM in the real phenotype analysis. Sib-tested animals from the sixth to the seventh generation were defined as test animals in all traits, and the number of test animals was 136. Four groups of animals with records were used for predicting the (G)EBV of test animals, and are defined as follows: all animals from the first to the fifth generation (ALL_G5), sib-tested animals from the second to the fifth generation (SIB_G5), all animals from the first to the seventh generation (ALL_G7), and all animals from the first to the fifth generation and non-sib-tested animals from the sixth to the seventh generation (ALL_nonSIB_G7). ALL_G5 and SIB_G5 are regarded as a reference population of normal genomic evaluation. ALL_G7 is comprised of all animals including test animals, and the test animals are regarded as the animals with records obtained from performance tests. ALL_nonSIB_G7 is comprised of all animals excluding test animals, and the test animals are regarded as the animals with records from full-sib testing. All four groups were applied in the simulation analysis. In the real phenotype analysis, both ALL_G5 and ALL_nonSIB_G7 were applied in the DG, LEA and BF analyses to represent a realistic situation. In the IMF analysis, only SIB_G5 was applied, because IMF was only measured in sib-tested animals. The accuracy of the (G)EBV was assessed using Pearson's correlation between the true value and the (G)EBV in test animals, and the regression coefficients of the true value on the (G)EBV in test animals were calculated to assess unbiasedness. The true value was assumed as the TBV in the simulated phenotype data and the adjusted phenotype, which was adjusted by the fixed effects, in the real phenotype data. In the simulation analysis, the mean and SD of 100 replicates was calculated in the combinations of different QTL effects (two analyses), animal groups (four analyses) and relationship matrices (three analyses).
Results
Difference between SNP- and haplotype-based GRMs
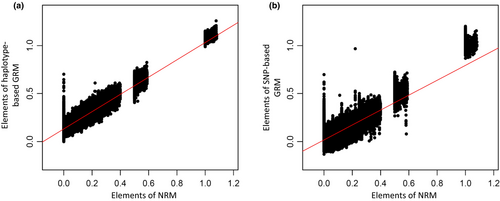
The regressions of elements in GRMs on those in the NRM are plotted in Figure 1. Diagonal and lower off-diagonal elements were plotted in each relationship matrix. In this study, the coefficient of determination (R2) of GH (0.86) was higher than that of GS (0.64), and a smaller variance of elements among animals in GH was shown than those in GS. The slope of GH (0.90) was higher than that of GS (0.78), and the elements of GS were more regressed than those of GH. The intercept of GH (0.13) was higher than that of GS (0.02), and the elements of GH were more overestimated than those of GS.
Heritability estimation
Estimated heritabilities in the simulation analysis are shown in Table 1. As for the sample size, the mean values of estimated heritability were close to the setting value (0.50) in sib-tested and all animals, but the SDs of the estimated heritability in sib-tested animals (from 0.11 to 0.17) were almost twice as high as those in all animals (from 0.06 to 0.08). As for the estimated values of heritability among the three relationship matrices, the mean value of the estimated heritability for GH was the highest in both QTL genotypes. For GS and the NRM, the trend of the estimated heritabilities in the SNP-QTL scenario (NRM ≤ GS) and that in the Haplotype-QTL scenario (GS < NRM) were shown, and it depended on the QTL genotype. For example, in all animals, the mean values of the estimated heritability for the NRM and GS were 0.53 in the SNP-QTL scenario, and 0.52 and 0.48 in the Haplotype-QTL scenario, respectively.
| Animals with records | Number | Matrixa | Estimated heritabilityb | |||
|---|---|---|---|---|---|---|
| SNP-QTLc | Haplotype-QTLc | |||||
| Mean | SD | Mean | SD | |||
| All animals | 831 | A | 0.53 | 0.07 | 0.52 | 0.08 |
| GH | 0.56 | 0.06 | 0.54 | 0.07 | ||
| GS | 0.53 | 0.06 | 0.48 | 0.07 | ||
| Sib-tested animals | 302 | A | 0.49 | 0.17 | 0.50 | 0.17 |
| GH | 0.54 | 0.12 | 0.52 | 0.13 | ||
| GS | 0.51 | 0.11 | 0.44 | 0.12 | ||
- a A, numerator relationship matrix; GH, Haplotyped-based genomic relationship matrix (GRM); GS, single nucleotide polymorphism (SNP)-based GRM.
- b The heritability of the simulated phenotype was set at 0.50.
- c Two different quantitative trait locus (QTL) genotypes were assumed.
In the real phenotype analysis, the estimated heritabilities for DG, LEA, BF and IMF are shown in Table 2. The standard errors (SEs) of the estimated heritability for IMF (from 0.11 to 0.16) were almost twice as high as those for the other three traits (from 0.05 to 0.08). As for the estimated values of heritability among the three relationship matrices, a large difference was not observed, but there was a slight trend in the results among these relationship matrices in DG, BF and IMF. The estimated heritability for GH was the highest, and the trend of the estimated heritabilities (NRM ≤ GS) was shown. For example, the estimated heritabilities of the NRM, GS, and GH in DG were 0.36, 0.37 and 0.39, and those in IMF were 0.52, 0.54 and 0.67, respectively. Comparatively, the estimated heritability of the NRM was the highest in LEA, and the estimated heritabilities of the NRM, GS,and GH were 0.56, 0.53 and 0.54, respectively.
| Traits | Abbreviation | Descriptive statistics | Estimated heritabilitya | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | GH | GS | ||||||||
| N | Mean | SD | Value | SE | Value | SE | Value | SE | ||
| Average daily gain from 30 to 105 kg of body weight (g/day) | DG | 779 | 1094.0 | 112.8 | 0.36 | 0.07 | 0.39 | 0.06 | 0.37 | 0.06 |
| Ultrasound loin eye muscle area (cm2) | LEA | 776 | 34.6 | 3.3 | 0.56 | 0.07 | 0.54 | 0.06 | 0.53 | 0.05 |
| Ultrasound backfat thickness (cm) | BF | 776 | 3.2 | 0.6 | 0.49 | 0.08 | 0.53 | 0.06 | 0.49 | 0.05 |
| Intramuscular fat content (%) | IMF | 302 | 5.0 | 1.6 | 0.52 | 0.16 | 0.67 | 0.11 | 0.54 | 0.11 |
- a A, Numerator relationship matrix; GH, Haplotyped-based genomic relationship matrix (GRM); GS, single nucleotide polymorphism (SNP)-based GRM.
Prediction accuracy
The correlation coefficients between the TBV and the (G)EBV obtained by three relationship matrices in the simulation analysis are shown in Table 3. In the simulation analysis, the correlation coefficients in the SNP-QTL scenario were higher than those in the Haplotype-QTL scenario. The correlation coefficients of the GRMs were higher than those of the NRM in each animal group and QTL genotype. There was no large difference in the results between GRMs, but there were slight trends in the correlation coefficien in the SNP-QTL scenario (GH < GS) and that of the Haplotype-QTL scenario (GS < GH) in all animal groups. For example, in ALL_G5, the correlation coefficients for GH and GS were 0.53 and 0.56 in the SNP-QTL scenario, and 0.51 and 0.48 in the Haplotype-QTL scenario, respectively. As for the comparison of the results among different animal groups, the increases in the correlation coefficient in ALL_G5 over SIB_G5 ranged from 0.18 to 0.21 in both QTL genotypes. The correlation coefficients in ALL_G7 were the highest of all animal groups, and the correlation coefficients of GRMs in ALL_G5 were close to that of the NRM in ALL_nonSIB_G7. For example, the correlation coefficient of GH in ALL_G5 was 0.51 and that of the NRM in ALL_nonSIB_G7 was 0.54 in the Haplotype-QTL scenario, and the correlation coefficient of GS in ALL_G5 was 0.56 and that of the NRM in ALL_nonSIB_G7 was 0.57 in the SNP-QTL scenario. The regression coefficients of TBV on the (G)EBV obtained by three relationship matrices in the simulation analysis are also shown in Table 3. The different SDs of the regression coefficients for ALL_G7 (from 0.08 to 0.11), ALL_nonSIB_G7 (from 0.12 to 0.19), ALL_G5 (from 0.21 to 0.35) and SIB_G5 (from 0.35 to 0.77) were shown, and thus the SDs of the regression coefficients strongly depended on the size of animals with records. As for the trend, the slight trend of the regression coefficients (GS < GH) was shown in both scenarios, and the regression coefficients obtained using the NRM was intermediate to these regression coefficients.
| Animals with records†‡ | Number | Matrixc | Correlation coefficients | Regression coefficients | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SNP-QTLd | Haplotype-QTLd | SNP-QTLd | Haplotype-QTLd | |||||||
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | |||
| ALL_G5 | 494 | A | 0.40 | 0.14 | 0.39 | 0.12 | 1.06 | 0.35 | 1.02 | 0.35 |
| GH | 0.53 | 0.11 | 0.51 | 0.10 | 1.11 | 0.24 | 1.06 | 0.23 | ||
| GS | 0.56 | 0.11 | 0.48 | 0.11 | 1.06 | 0.21 | 0.91 | 0.22 | ||
| SIB_G5 | 166 | A | 0.22 | 0.14 | 0.21 | 0.15 | 1.08 | 0.74 | 1.02 | 0.77 |
| GH | 0.33 | 0.12 | 0.33 | 0.13 | 1.08 | 0.41 | 1.06 | 0.44 | ||
| GS | 0.36 | 0.12 | 0.30 | 0.13 | 1.01 | 0.35 | 0.84 | 0.37 | ||
| ALL_G7 | 831 | A | 0.78 | 0.05 | 0.77 | 0.05 | 1.07 | 0.09 | 1.03 | 0.11 |
| GH | 0.82 | 0.04 | 0.81 | 0.05 | 1.07 | 0.08 | 1.05 | 0.10 | ||
| GS | 0.83 | 0.04 | 0.79 | 0.05 | 1.05 | 0.08 | 1.02 | 0.10 | ||
| ALL_nonSIB_G7 | 695 | A | 0.57 | 0.09 | 0.54 | 0.10 | 1.05 | 0.17 | 1.00 | 0.19 |
| GH | 0.68 | 0.07 | 0.66 | 0.08 | 1.08 | 0.13 | 1.04 | 0.15 | ||
| GS | 0.71 | 0.07 | 0.63 | 0.08 | 1.05 | 0.12 | 0.95 | 0.14 | ||
- a The heritability of the simulated phenotype was set at 0.50.
- b ALL_G5, all animals comprised from the first to the fifth generation; SIB_G5, sib-tested animals comprised from the second to the fifth generation; ALL_G7, all animals comprised from the first to the seventh generation; ALL_nonSIB_G7, all animals comprised from the first to the fifth generation and non-sib-tested animals comprised from the sixth to the seventh generation.
- c A, Numerator relationship matrix; GH, Haplotyped-based genomic relationship matrix (GRM); GS, single nucleotide polymorphism (SNP)-based GRM.
- d Two different quantitative trait locus (QTL) genotypes are assumed.
In the real phenotype analysis, the correlation coefficients between adjusted phenotypes and the (G)EBV obtained by three relationship matrices are shown in Table 4. The correlation coefficients of GRMs were higher than that of the NRM. There was no large difference observed in the results between GRMs for all traits, but there were slight trends in the correlation coefficient (GH ≤ GS) for all traits. For example, for DG in ALL_G5, the correlation coefficients of the NRM, GH and GS were 0.28, 0.34 and 0.35, respectively. In the comparison of the results between ALL_G5 and ALL_nonSIB_G7, the correlation coefficients of GRMs in ALL_G5 (0.33) were higher than that of the NRM in ALL_nonSIB_G7 (0.31) for LEA. The regression coefficients of adjusted phenotypes on the (G)EBV are also shown in Table 4, but no large trend of the results among these relationship matrices was observed in these traits.
| Animals with recordsa | Number | Traitsb | Correlation coefficientsc | Regression coefficientsc | ||||
|---|---|---|---|---|---|---|---|---|
| A | GH | GS | A | GH | GS | |||
| ALL_G5 | 447 | DG | 0.28 | 0.34 | 0.35 | 1.82 | 1.55 | 1.46 |
| 444 | LEA | 0.20 | 0.33 | 0.33 | 1.09 | 1.12 | 1.01 | |
| 444 | BF | 0.19 | 0.22 | 0.25 | 0.80 | 0.71 | 0.72 | |
| 166 | IMFd | 0.17 | 0.37 | 0.38 | 0.96 | 1.50 | 1.22 | |
| ALL_nonSIB_G7 | 643 | DG | 0.39 | 0.45 | 0.48 | 1.16 | 1.21 | 1.25 |
| 640 | LEA | 0.31 | 0.41 | 0.47 | 0.90 | 0.96 | 1.08 | |
| 640 | BF | 0.28 | 0.33 | 0.35 | 0.80 | 0.82 | 0.82 | |
- a ALL_G5, all animals comprised from the first to the fifth generation; ALL_nonSIB_G7, all animals comprised from the first to the fifth generation and non-sib-tested animals comprised from the sixth to the seventh generation.
- b DG, average daily gain from 30 to 105 kg of body weight; LEA, ultrasonically measured loin eye muscle area; BF, backfat thickness at 105 kg weight; IMF, intramuscular fat content.
- c A, Numerator relationship matrix; GH, Haplotyped-based genomic relationship matrix (GRM); GS, single nucleotide polymorphism (SNP)-based GRM.
- d Sib-tested animals comprised from the second to the fifth generation.
Discussion
In this study, we evaluated the impact of three different relationship matrices on heritability estimation and the prediction accuracy of (G)EBV utilizing a simulation analysis and real phenotype analysis. The difference between the NRM and GRMs is whether Mendelian segregation is being considered at the genome level. In addition, three relationship matrices refer to the relationships of differently aged pigs (very recent, intermediate-aged and very old relationships) in a population (Meuwissen et al. 2014). The NRM assumes that animals are unrelated in a base population, and the genetic relationships among animals after the base population are expressed by Identity-By-Descent (IBD) probabilities (Wright 1922). The probability that two alleles are IBD is calculated using a known pedigree, and the founders are a base population in the pedigree. The base populations in the pedigree are usually quite recent, and thus the NRM traces only very recent genetic relationships in a population. Comparatively, the genetic relationships among animals in SNP-based GRMs are the probabilities based on alleles at SNPs being Identical-By-State (IBS) (Powell et al. 2010). When the inheritance of the two alleles is traced back in time, their paths of inheritance eventually coalesce into a common ancestor. Therefore, alleles which are IBS are also IBD, owing to an old relationship obtained by tracing back to an ancient common ancestor, and consequently SNP-based GRMs overestimate the variance in a relationship (Powell et al. 2010; Meuwissen et al. 2014). In addition, the relationship based on ancestral haplotypes can account for the relationship of intermediate ages (Meuwissen et al. 2014). Recombination of haplotypes occurs more frequently than mutations at SNPs, and thus the inheritance of the two haplotypes could trace intermediate-aged relationships in a population. In this study, the regression of elements in two GRMs on those in the NRM showed that higher values of R2 and slopes for GH were obtained than those for GS. This means that the variance in the relationship for GS was overestimated compared with that for GH, and GH was closer to the NRM than GS. Consequently, GH reflected the relationship of intermediate ages between GS and the NRM in this population. Meuwissen et al. (2014) reported that intermediate-aged relationships could yield more accurate genomic predictions than very recent relationships (i.e. the NRM) and very old relationships (i.e. GS). Therefore, we applied these different relationship matrices for heritability estimation and prediction accuracy.
In this study, the adjusted matrix was used in SNP-based GRM by scaling to the allele frequencies in the base population to account for bias resulting from selection (Chen et al. 2011; Forni et al. 2011; Vitezica et al. 2011). In IBD-based evaluation such as those using NRM and GH, all information about selection is included in the relationship matrix, because genetic relationship and inbreeding coefficients from young animals are estimated as deviations from the unselected base relatedness. Thus, no bias exists resulting from selection. However, IBS-based evaluation such as that using G0 does not take this selection into account, because G0 is assumed using the allele frequencies of the unselected base population. In this population, animals are a closed-line breeding population, and thus the SNP-based GRM must be scaled to be the allele frequencies in the base population. In preliminary analysis, heritability estimation and prediction accuracy using adjusted and unadjusted SNP-based GRM were performed in the simulation analysis (see Table S1). The results showed that the estimated heritabilities and the regression coefficients for adjusted SNP-based GRM (i.e. GS) were slightly higher than those for unadjusted SNP-based GRM (i.e. G0), and thus the adjusted SNP-based GRM was used in this study.
For heritability estimation, two animal groups (all animals and sib-tested animals) were applied in heritability estimation for evaluating the impact of sample size. The results for all and sib-tested animals showed that the accuracy of estimated heritability depends on the size of animals with records, and thus a larger sample size is needed to obtain a reliable heritability estimate. In the results for all animals, a large difference was not shown among the three relationship matrices, but there was a trend among the results of these matrices. In the simulation study, the trend of the estimated heritability among the three relationship matrices was NRM ≤ GS < GH in the SNP-QTL scenario and GS < NRM < GH in the Haplotype-QTL scenario. These trends could be caused by the extent of LD between QTL and SNPs in the SNP array. In the simulation analysis, some LD in the Haplotype-QTL scenario and perfect LD in the SNP-QTL scenario were assumed between QTL and SNPs in the SNP array. In addition, the QTL effect was generated from a gamma distribution, which means total genetic variance is composed of a few QTL with large and polygenic effects (Hayes & Goddard 2001). For GH, GH could overestimate the QTL variance around QTL and thus overestimate the total genetic variance, because haplotype-based GWAS cannot perform finer mapping than SNP-based GWAS does in this population (Sato et al. 2016). For GS and the NRM, the trends of the estimated heritability (NRM ≤ GS) were shown in the SNP-QTL scenario, because GS could capture all of the total genetic variance under perfect LD between QTL and SNPs on the array. Comparatively, imperfect LD between QTL and SNPs on the array could cause the underestimation of total genetic variance in GS, and thus the trend of the estimated heritability (GS < NRM) was shown in the Haplotype-QTL analysis. In the real phenotype analysis, the trend of the estimated heritability (NRM ≤ GS < GH) was shown in DG, BF and IMF. In LEA, the estimated heritability of the NRM was the highest in all three matrices. In DG and BF, suggestive QTL were detected by haplotype-based GWAS, but no QTL were detected in LEA (Sato et al. 2016). In addition, significant QTL were detected by SNP-based GWAS in DG and BF, but not detected in LEA (Sato et al. 2016). As for IMF, no QTL was detected by haplotype-based GWAS, but some suggestive QTL on chromosome 7 located in a similar region were detected by SNP-based GWAS (Sato et al. 2016). The extent of LD was very high in this population, because moderate LD (r2 = 0.20) extended to about 1.0 Mbp in this population (Sato et al. 2016). Therefore, these QTL would be in very strong LD with the SNPs on the array, and thus these traits could show the similar trend of the estimated heritability in the simulation of the SNP-QTL scenario. Comparatively, polygenic effects could contribute to the total genetic variance in LEA in this population, and thus the estimated heritability for the NRM was the highest. Our results also implied that comparing the results of three relationship matrices could assist in evaluating the impact of QTL on the total genetic variance.
For prediction accuracy of the (G)EBV, the results of the simulation analysis and the real phenotype analysis showed that the accuracies of the GEBV by GRMs were higher than the EBV by the NRM in all animal groups. A large difference in the results between GRMs was not shown but there were slight trends in the correlation coefficient (GH ≤ GS) for the SNP-QTL scenario and the real phenotype analysis. Some reports showed that using haplotypes in genomic evaluation has a higher accuracy than using SNPs in simulation studies (Calus et al. 2008), pig populations (Meuwissen et al. 2014) and cattle populations (De Roos et al. 2011). Calus et al. (2008) also suggested that the advantage of using haplotypes in genomic evaluation decreased as the marker density was increased. In this study, the larger extent of LD and the use of tens of thousands of SNPs would decrease the advantage of using haplotypes, and thus the higher accuracy of the GEBV for GS was shown compared with that for GH. Therefore, genomic evaluation using GS would be a realistic approach in a closed-line breeding population, if tens of thousands of SNPs are used. In closed-line breeding, some traits such as meat quality are measured in only a small number of sib-tested animals, and thus SIB_G5 was applied for evaluating the impact of sample size. The comparison of the results between ALL_G5 and SIB_G5 showed that the accuracy of the (G)EBV depends on the number of animals with records. Many factors influence the accuracy of the (G)EBV, and in particular the accuracy strongly depends on the number of animals in the reference population (Daetwyler et al. 2010; Uemoto et al. 2015). Therefore, genomic evaluation with a larger number of animals could improve the accuracy of the (G)EBV in a closed-line breeding population. In closed-line breeding, pigs with records obtained through a performance test or by full-sib testing are normally used for obtaining an EBV, and thus ALL_G7 and ALL_nonSIB_G7 were also applied for comparing the results of normal genomic evaluation (i.e. ALL_G5). The accuracies of the GEBV by GRMs in ALL_G5 were lower than the EBV obtained by the NRM in ALL_G7, but were close to and higher than the EBV obtained by the NRM in ALL_nonSIB_G7 in the simulation analysis and in LEA, respectively. Therefore, the GEBV predicted using ALL_G5 could be an alternative selection indicator instead of the EBV obtained by full-sib testing.
For unbiasedness of the (G)EBV, the accuracy of the regression coefficients strongly depended on the number of animals for which records were available. In this study, the sample size is relatively small, and thus the trend was not shown in real phenotype analysis because of the low accuracy of the regression coefficients. However, the slight trend of the regression coefficients (GS < GH) was shown in the simulation analysis, and this trend is similar to the results as described by Luan et al. (2012). Luan et al. (2012) reported that the regression coefficients obtained using IBD information were higher than that using IBS information in a dairy cattle population. In addition, the unbiasedness depended on the extent of LD between SNPs and QTL. The regression coefficients using GS were close to 1 in the SNP-QTL scenario, but those using GH were close to 1 in the Haplotye-QTL scenario. On the other hand, the regression coefficients obtained using the NRM were constantly close to 1 in both scenarios. Since the regression coefficients obtained using the NRM are expected to be unbiased, comparing the regression coefficients obtained using three relationship matrices could assist in evaluating the extent of LD between SNPs and QTLs.
In the simulation analysis, we assumed the SNP-QTL and Haplotype-QTL scenarios. The Haplotype-QTL scenario (i.e. SNPs are not QTL) is a realistic assumption in an actual pig population, but the results of the real phenotype analysis for GRMs formed a similar trend to that of the SNP-QTL scenario in heritability estimation and prediction accuracy. Therefore, this result indicated that the extent of LD between QTL and SNPs in the SNP array would be close to the perfect LD in a closed-line breeding population. The SNP-QTL scenario was also applied to obtain the maximum value of prediction accuracy in genomic evaluation using this population. The accuracies of (G)EBV in the SNP-QTL scenario were higher than those in the Haplotype-QTL scenario. In the SNP-QTL scenario, the correlation coefficient of GS in ALL_G5 was 0.56 and that of the NRM in ALL_G7 was 0.78. The results showed that the GEBV in the genomic evaluation was less accurate than the EBV in normal BLUP evaluation using animals with records, even if SNPs in the SNP array were QTL. One of the other approaches for improving the prediction of the GEBV is using only QTL detected with a large effect. For example, Ros-Freixedes et al. (2016) reported that the accuracies of the GEBV using leptin receptor (LEPR) gene was higher than that using SNPs in the SNP array except for the gene locus in intramuscular fat content in a pig population. In this population, the preferable allele frequency of LEPR was very high (0.975) (Sato et al. 2016), and LEPR could not be applied in this study. However, genomic evaluation using a few QTL could be an effective method to predict the GEBV, if QTL were already detected in a previous study and these QTL had a large effect on the objective traits and moderate MAF.
The current study evaluated the impact of three different relationship matrices on heritability estimation and the prediction accuracy in closed-line breeding of Duroc pigs. The accuracy of estimated heritability and (G)EBV prediction depended on the number of animals with records. For heritability estimation, a large difference in the results among three relationship matrices was not shown, but there was a trend among the results of two GRMs (GS < GH). The estimated heritability for GH was overestimated, when QTL were in perfect LD with the SNPs in the SNP array. For prediction accuracy, the results of the simulation analysis and the real phenotype analysis showed that the accuracies of the GEBV by GRMs were higher than that of the EBV by the NRM. In addition, there were slight trends in the accuracy of the GEBV (GH ≤ GS) for the SNP-QTL scenario and the real phenotype analysis. Therefore, genomic evaluation using GS could be a realistic approach in a closed-line breeding population, if tens of thousands of SNPs are used. The accuracies of the GEBV by GRMs in ALL_G5 were lower than that of the EBV by the NRM in ALL_G7, but were close to and higher than the EBV obtained by the NRM in ALL_nonSIB_G7 in the simulation study and in LEA, respectively. Therefore, the GEBV predicted using ALL_G5 could be an alternative selection indicator instead of the EBV obtained by full-sib testing.
Acknowledgments
Funding for PorcineSNP60 BeadChip genotyping was provided by the private association project for stepped-up measures of agricultural competitive positions in 2013 and 2014 from the Ministry of Agriculture, Forestry and Fisheries of Japan.
