The real- and redshift-space density distribution functions for large-scale structure in the spherical collapse approximation

We use the spherical collapse (SC) approximation to derive expressions for the smoothed redshift-space probability distribution function (PDF), as well as the p-order hierarchical amplitudes S_p, in both real and redshift space. We compare our results with numerical simulations, focusing on the standard CDM model, where redshift distortions are strongest. We find good agreement between the SC predictions and the numerical PDF in real space even for , where σ_L is the linearly evolved rms fluctuation on the smoothing scale. In redshift space, reasonable agreement is possible only for . Numerical simulations also yield a simple empirical relation between the real-space PDF and the redshift-space PDF: we find that for 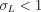, the redshift-space PDF, [Pδ_(z)], is, to a good approximation, a simple rescaling of the real-space PDF, P[δ], i.e., whereσ and σ_(z) are the real-space and redshift-space rms fluctuations, respectively. This result applies well beyond the validity of linear perturbation theory, and it is a good fit for both the standard CDM model and the ΛCDM model. It breaks down for SCDM at 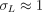, but provides a good fit to the ΛCDM models for σ_L as large as 0.8.