One-step validation method for surrogate endpoints using data from multiple randomized cancer clinical trials with failure-time endpoints
Corresponding Author
Casimir Ledoux Sofeu
INSERM U1219 (Biostatistic), Université Bordeaux Segalen, Bordeaux, France
Casimir Ledoux Sofeu, INSERM U1219 (Biostatistic), Université Bordeaux Segalen, 146 rue Léo Saignat, 33076 Bordeaux Cedex, France.
Email: [email protected]; [email protected]
Search for more papers by this authorTakeshi Emura
Graduate Institute of Statistics, National Central University, Taoyuan, Taiwan
Search for more papers by this authorVirginie Rondeau
INSERM U1219 (Biostatistic), Université Bordeaux Segalen, Bordeaux, France
Search for more papers by this authorCorresponding Author
Casimir Ledoux Sofeu
INSERM U1219 (Biostatistic), Université Bordeaux Segalen, Bordeaux, France
Casimir Ledoux Sofeu, INSERM U1219 (Biostatistic), Université Bordeaux Segalen, 146 rue Léo Saignat, 33076 Bordeaux Cedex, France.
Email: [email protected]; [email protected]
Search for more papers by this authorTakeshi Emura
Graduate Institute of Statistics, National Central University, Taoyuan, Taiwan
Search for more papers by this authorVirginie Rondeau
INSERM U1219 (Biostatistic), Université Bordeaux Segalen, Bordeaux, France
Search for more papers by this authorAbstract
A surrogate endpoint can be used instead of the most relevant clinical endpoint to assess the efficiency of a new treatment. Before being used, a surrogate endpoint must be validated based on appropriate methods. Numerous validation approaches have been proposed with the most popular used in a context of meta-analysis, based on a two-step analysis strategy. For two failure-time endpoints, two association measurements are usually used, Kendall's τ at the individual level and the adjusted coefficient of determination (
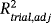 ) at the trial level. However,
) at the trial level. However,
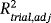 is not always available due to model estimation constraints. We propose a one-step validation approach based on a joint frailty model, including both individual-level and trial-level random effects. Parameters have been estimated using a semiparametric penalized marginal log-likelihood method, and various numerical integration approaches were considered. Both individual- and trial-level surrogacy were evaluated using a new definition of Kendall's τ and the coefficient of determination. Estimators' performances were evaluated using simulation studies and satisfactory results were found. The model was applied to individual patient data meta-analyses in gastric cancer to assess disease-free survival as a surrogate for overall survival, as part of the evaluation of adjuvant therapy.
is not always available due to model estimation constraints. We propose a one-step validation approach based on a joint frailty model, including both individual-level and trial-level random effects. Parameters have been estimated using a semiparametric penalized marginal log-likelihood method, and various numerical integration approaches were considered. Both individual- and trial-level surrogacy were evaluated using a new definition of Kendall's τ and the coefficient of determination. Estimators' performances were evaluated using simulation studies and satisfactory results were found. The model was applied to individual patient data meta-analyses in gastric cancer to assess disease-free survival as a surrogate for overall survival, as part of the evaluation of adjuvant therapy.
Supporting Information
The reader is referred to the Supplementary information for technical appendices and additional simulations referenced in Sections 2, 3, and 4. Elements included are as follows:
- A. Log-likelihood construction associated with the proposed joint surrogate model;
- B. Kendall's τ derivation;
- C. Nonconvergence case management procedure;
- D. Additional simulation results.
| Filename | Description |
|---|---|
| SIM_8162-Supp-0001-Supporting Information.pdfPDF document, 153.9 KB |
SIM_8162-Supp-0001-Supporting Information.pdf |
| SIM_8162-Supp-0002-Supporting Information.texapplication/tex, 22.5 KB |
SIM_8162-Supp-0002-Supporting Information.tex |
Please note: The publisher is not responsible for the content or functionality of any supporting information supplied by the authors. Any queries (other than missing content) should be directed to the corresponding author for the article.
REFERENCES
- 1Fleming TR, Prentice RL, Pepe MS, Glidden D. Surrogate and auxiliary endpoints in clinical trials, with potential applications in cancer and aids research. Statist Med. 1994; 13(9): 955-968.
- 2Ellenberg SS, Hamilton JM. Surrogate endpoints in clinical trials: cancer. Statist Med. 1989; 8(4): 405-413.
- 3Baker SG, Kramer BS. A perfect correlate does not a surrogate make. BMC Med Res Methodol. 2003; 3(1): 16.
- 4Fleming TR, DeMets DL. Surrogate end points in clinical trials: are we being misled? Ann Intern Med. 1996; 125(7): 605-613.
- 5Prentice RL. Surrogate endpoints in clinical trials: definition and operational criteria. Statist Med. 1989; 8(4): 431-440.
- 6Freedman LS, Graubard BI, Schatzkin A. Statistical validation of intermediate endpoints for chronic diseases. Statist Med. 1992; 11(2): 167-178.
- 7Buyse M, Molenberghs G. Criteria for the validation of surrogate endpoints in randomized experiments. Biometrics. 1998; 54(3): 1014-1029.
- 8Buyse M, Molenberghs G, Burzykowski T, Renard D, Geys H. The validation of surrogate endpoints in meta-analyses of randomized experiments. Biostatistics. 2000; 1(1): 49-67.
- 9Alonso A, Molenberghs G, Geys H, Buyse M, Vangeneugden T. A unifying approach for surrogate marker validation based on prentice's criteria. Statist Med. 2006; 25(2): 205-221.
- 10Renfro LA, Shi Q, Sargent DJ, Carlin BP. Bayesian adjusted R2 for the meta-analytic evaluation of surrogate time-to-event endpoints in clinical trials. Statist Med. 2012; 31(8): 743-761.
- 11Li Y, Taylor JMG, Elliott MR, Sargent DJ. Causal assessment of surrogacy in a meta-analysis of colorectal cancer trials. Biostatistics. 2011; 12(3): 478-492.
- 12Frangakis CE, Rubin DB. Principal stratification in causal inference. Biometrics. 2002; 58(1): 21-29.
- 13Rotolo F, Paoletti X, Burzykowski T, Buyse M, Michiels S. A poisson approach to the validation of failure time surrogate endpoints in individual patient data meta-analyses. Stat Methods Med Res. 2017; 28(1): 170-183.
- 14Buyse M, Molenberghs G, Paoletti X, et al. Statistical evaluation of surrogate endpoints with examples from cancer clinical trials. Biom J. 2016; 58(1): 104-132.
- 15Burzykowski T, Molenberghs G, Buyse M, Geys H, Renard D. Validation of surrogate end points in multiple randomized clinical trials with failure time end points. J R Stat Soc Ser C Appl Stat. 2001; 50(4): 405-422.
- 16Burzykowski T, Molenberghs G, Buyse M. The Evaluation of Surrogate Endpoints. New York, NY: Springer; 2005.
10.1007/b138566 Google Scholar
- 17Emura T, Nakatochi M, Murotani K, Rondeau V. A joint frailty-copula model between tumour progression and death for meta-analysis. Stat Methods Med Res. 2017; 26(6): 2649-2666.
- 18Rondeau V, Pignon J-P, Michiels S. A joint model for the dependence between clustered times to tumour progression and deaths: a meta-analysis of chemotherapy in head and neck cancer. Stat Methods Med Res. 2015; 24(6): 711-729.
- 19Rondeau V, Mathoulin-Pelissier S, Jacqmin-Gadda H, Brouste V, Soubeyran P. Joint frailty models for recurring events and death using maximum penalized likelihood estimation: application on cancer events. Biostatistics. 2007; 8(4): 708-721.
- 20Yu Z, Liu L, Bravata DM, Williams LS. Joint model of recurrent events and a terminal event with time-varying coefficients. Biometrical Journal. 2014; 56(2): 183-197.
- 21Huang X, Liu L. A joint frailty model for survival and gap times between recurrent events. Biometrics. 2007; 63(2): 389-397.
- 22Rizopoulos D. Fast fitting of joint models for longitudinal and event time data using a pseudo-adaptive Gaussian quadrature rule. Comput Stat Data Anal. 2012; 56(3): 491-501.
- 23O'Sullivan F. Fast computation of fully automated log-density and log-hazard estimators. SIAM J Sci and Stat Comput. 1988; 9(2): 363-379.
- 24Joly P, Commenges D, Letenneur L. A penalized likelihood approach for arbitrarily censored and truncated data: application to age-specific incidence of dementia. Biometrics. 1998; 54(1): 185-194.
- 25Ramsay JO. Monotone regression splines in action. Statistical Science. 1988; 3(4): 425-441.
10.1214/ss/1177012761 Google Scholar
- 26Rondeau V, Commenges D, Joly P. Maximum penalized likelihood estimation in frailty models. Lifetime Data Anal. 2003; 9(2): 139-153.
- 27Marquardt DW. An algorithm for least-squares estimation of nonlinear parameters. J Soc Ind Appl Math. 1963; 11(2): 431-441.
- 28Kendall MG. Rank Correlation Methods. 2nd ed. New York, NY: Hafner Press; 1955.
- 29Duchateau L, Janssen P. The Frailty Model. New York, NY: Springer; 2008.
- 30 The GASTRIC Group. Benefit of adjuvant chemotherapy for resectable gastric cancer: a meta-analysis. JAMA. 2010; 303(17): 1729-1737.
- 31Oba K, Paoletti X, Alberts S, et al. Disease-free survival as a surrogate for overall survival in adjuvant trials of gastric cancer: a meta-analysis. J Natl Cancer Inst. 2013; 105(21): 1600-1607.
- 32Crowther MJ, Riley RD, Staessen JA, Wang J, Gueyffier F, Lambert PC. Individual patient data meta-analysis of survival data using poisson regression models. BMC Med Res Methodol. 2012; 12(1): 34.
- 33Mazroui Y, Mathoulin-Pelissier S, Soubeyran P, Rondeau V. General joint frailty model for recurrent event data with a dependent terminal event: application to follicular lymphoma data. Statist Med. 2012; 31(11-12): 1162-1176.
- 34Ferrer L, Rondeau V, Dignam J, Pickles T, Jacqmin-Gadda H, Proust-Lima C. Joint modelling of longitudinal and multi-state processes: application to clinical progressions in prostate cancer. Statist Med. 2017; 35(22): 3933-3948.
- 35Shi Q, Renfro LA, Bot BM, Burzykowski T, Buyse M, Sargent DJ. Comparative assessment of trial-level surrogacy measures for candidate time-to-event surrogate endpoints in clinical trials. Comput Stat Data Anal. 2011; 55(9): 2748-2757.
- 36Kròl A, Mauguen A, Mazroui Y, Laurent A, Michiels S, Rondeau V. Tutorial in joint modeling and prediction: a statistical software for correlated longitudinal outcomes, recurrent events and a terminal event. J Stat Softw. 2017; 81(3): 1-52.
- 37Rotolo F, Paoletti X, Michiels S. Surrosurv: an R package for the evaluation of failure time surrogate endpoints in individual patient data meta-analyses of randomized clinical trials. Comput Methods Programs Biomed. 2018; 155: 189-198.




