Time delay control with sliding mode observer for a class of nonlinear systems: Performance and stability
Abstract
Time delay control (TDC) is a type of disturbance observer (DO)-based control, where the disturbance estimation is performed by using the past information of control input and measurement signals. Despite its capability, there are concerns about its practical implementation. First, it requires acceleration measurements which are generally not available in many industrial systems. Second, input delays are introduced into the closed-loop system, but the relation between the size of the delay and the performance of TDC has not been studied. Finally, there is a lack of tools to analyze its performance in disturbance estimation and robust stability for a given set of control parameters. We construct Lyapunov–Krasovskii functionals for a class of nonlinear systems which leads to delay-dependent conditions in linear matrix inequalities (LMIs) for the ultimate boundedness of the closed-loop system. This provides a means for analyzing the trade-off between the accuracy of disturbance estimation and robust stability. To circumvent acceleration measurements, we construct a sliding mode (SM) observer where the resulting error dynamics turns into a neutral type delay system. The existence conditions of both the SM control and SM observer are provided via a single LMI. A simulation example considering the tracking control of an autonomous underwater vehicle at constant and varying speed with a comparison to a non-TDC shows the effectiveness of the proposed method.
1 INTRODUCTION
The technique of time delay control (TDC) has been originally developed to compensate for system uncertainties, for example, unmodeled dynamics, parameter variations, and the effect of disturbances. The technique utilizes the past information of the control input and measurement signals to estimate the effect of the nonlinearities and disturbances.1, 2 While delays are considered to be undesirable in many systems, it might also have a stabilizing effect, see References 3-5. For introduction to the topic of time delay systems, please refer to References 6, 7, or 8. Another popular and effective robust control strategy is sliding mode control (SMC). It is well known for its inherent robust property against a class of unmeasurable disturbances and uncertainties.9 There are more recent advances in SMC. Gonzalez et al.10 considered finite-time convergence problem in variable gain super-twisting SMC for matched perturbations/uncertainties that are Lipschitz-continuous. An adaptive continuous higher order SMC was designed to mitigate the chattering effect.11 SMC based on finite-time boundedness for a class of nonlinear systems was investigated in Reference 12. A dissipativity-based SMC of continuously switched stochastic systems was proposed in Reference 13. A more recent collection of SMC advances and applications can be found in Reference 14. Combining robust control strategies such as SMC with methods that give estimates of uncertainties and disturbances is an attractive proposition. Such a combination enables a reduction in the magnitude of discontinuous components in the control and thereby offers the possibility of mitigating the chattering in control. Such control strategy and its applications can be found in References 15-17.
TDC has been applied in experimental environment in many systems.18-25 Despite its robustness, there are some critics about the usage of TDC.26, 27 There is a lack of guidelines for how to select the TDC parameters for disturbance estimation and feedback controller gains. The delay is usually chosen as the smallest sample size available in digital control. But these delays introduced to the control inputs may cause stability issues and make the stability analysis quite complicated. To what size of the delay the closed-loop system can tolerate is yet to be investigated. SMC under input delay was investigated, see, for example, Reference 28, where ultimate bounded stability was derived. In addition, TDC requires acceleration measurements. This limits its application as the acceleration measurements are generally not available in many industrial systems. It is also difficult to construct the acceleration signal from the velocity signal by differentiation due to injection of noise with discrete time-derivation. Another problem as pointed out in Reference 29 is that in the presence of so-called hard nonlinearities, such as saturation or static friction, TDC reveals some problems commonly found in other methods, like PID control or disturbance observer (DO). An increase in the command input or the response speed leads to (or would lead to) large over-shoots, limit cycles, or even unstable responses on the outputs. A simple frequency domain analysis shows that TDC contains a natural integral action, which is generated from the time-delayed estimation of the uncertainties and disturbance. Owing to the integral action, therefore, when an actuator has a saturation element, a wind-up phenomenon occurs as the control input increases. Hence, the design of disturbance estimation has to be considered together with the design of the controller gains to prevent the wind-up phenomenon. While TDC has shown promising results in experimental studies, literature rigorously analyzing these aspects that delimit the capabilities of TDC is scarce. How a system would respond to larger size of delays and how the disturbance estimation parameters and controller gains are to be selected so that the natural integral action in TDC is prevented from destabilizing the system are still to be investigated.
While there has been a lack of theoretical results in TDC to explore its full capability and performance limits, there are on-going efforts in studying other type of disturbance estimation methods which originated from the same concept as TDC. A nonlinear disturbance observer (NDO), which circumvents the need to use delays and acceleration measurements, was proposed in Reference 30 to estimate constant disturbance torques caused by unknown friction in robotic manipulators. An additional variable is introduced to avoid the measurement of the acceleration signals, in the form of an either linear or nonlinear functions. However, the resulting error of disturbance estimation in NDO depends on the derivative of the disturbances, whereas the resulting error of disturbance estimation in TDC only depends on the difference of the disturbance over the delay duration. The bound on the derivative of the disturbances can much greater than the bound on the time difference of the disturbance. This restricts the NDO to account for a typical type of disturbances with some known properties. A harmonic disturbance was considered in Reference 31 with known frequency but unknown amplitude and phase rather than constant ones. Based on this, an enhanced version of DO is also provided. In Reference 32, a disturbance estimator which requires the full knowledge of the nonlinearities was designed, so that it is fully compensated in the disturbance estimation error. Hence, the disturbance error dynamics is free from the control input, exemplifying the separation principle, that is, separating the design of controller and DO into two tasks. First, a state feedback controller that stabilizes the system and meets other design specifications is designed. Then, a DO is obtained which minimizes the error between the disturbances and its estimates provided by the DO.
Another disturbance observation technique, which is originated from TDC is developed in Reference 26, where it was shown in frequency domain that a low-pass filter or an uncertainty and disturbance estimator (UDE) which does not use acceleration measurements can be designed and its performance was shown to be comparable to that of TDC. In Reference 27, a study was performed to provide uncertainty and disturbance estimation for linear uncertain systems. A detailed filter was designed to cover both the low and high frequency range for attenuating the disturbance estimation error. The control gain can be increased arbitrarily to attenuate the disturbance estimation error. A modified UDE was used in Reference 33 to compensate for model uncertainties and reject input disturbances for quadrotors with input/output delays. None of the methods, that is, DO and UDE, have considered the effect of the controller gain on the bounding of the disturbance estimation error which is a function of the control inputs, meaning that larger controller gains designed for attenuating the disturbance estimation error could increase the estimation error and consequently violate the stability conditions. A comprehensive overview of disturbance-observer-based control (DOBC) can be found in Reference 34. Their limitations and further improvements can be summarized in the following two points. First, as a limitation, DOBC requires all of the states to be available, the low-pass filter, designed in frequency domain, still largely depends on tuning (under certain guidance). Second, as a question for further improvement, what is the limit of this approach? How to analyze the robust stability and performance for a designed DOBC strategy? For a prescribed level of the uncertainties and nonlinearities, how to develop a strategy that requires a minimum level of feedback and control bandwidth?
In this article, we attempt to tackle the above challenging questions by considering a sliding mode (SM) observer-based TDC control using only position and velocity measurements. The acceleration signal is estimated using a SM observer. In the literature of SM observer and controller for time delay systems, a SM observer for uncertain time delay systems was designed in Reference 35, where matched uncertainties and nonlinearities are considered. SMC for systems with delays, matched and mismatched model uncertainties, and external disturbances was performed in Reference 36. Readers are referred to Reference 37 for a comprehensive survey of SM observers. In this article, the system nonlinearities are assumed to be locally bounded by Lipschitz constants. We consider the effect of the controller and observer gains on the disturbance estimation error dynamics, and propose LMI conditions for minimizing the ultimate bound of the observer-based control system under either constant or varying delay. The resulting ultimate bound depends on the nonlinearities of the system which include external disturbances, controller and state observer inputs, and the generated reference speed signals. A scaling matrix 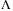 is introduced for tuning the trade-off between the accuracy of nonlinearity-disturbance estimation and robust stability depending on the size of the delay and its varying rate. It is shown that the resulting closed-loop system exhibits a delay system of a neutral type. For larger nonlinearities associated with larger speed variations, the scaling matrix needs to be reduced, implying a reduced estimation accuracy for increased stability. Hence, the proposed strategy prevents the problem of large overshoot and unstable responses in the output due to an increase in the command input, which commonly occurs with PID or DO-based controllers. The conditions for the existence SM for both the observer and the error neutral delay systems are provided in a single LMI. Based on the ultimate bound, a dynamical switching gain is designed to minimize the impact of the input-dependent TDC estimation error.
is introduced for tuning the trade-off between the accuracy of nonlinearity-disturbance estimation and robust stability depending on the size of the delay and its varying rate. It is shown that the resulting closed-loop system exhibits a delay system of a neutral type. For larger nonlinearities associated with larger speed variations, the scaling matrix needs to be reduced, implying a reduced estimation accuracy for increased stability. Hence, the proposed strategy prevents the problem of large overshoot and unstable responses in the output due to an increase in the command input, which commonly occurs with PID or DO-based controllers. The conditions for the existence SM for both the observer and the error neutral delay systems are provided in a single LMI. Based on the ultimate bound, a dynamical switching gain is designed to minimize the impact of the input-dependent TDC estimation error.
In Section 2, the generic model of the type of nonlinear system considered in this study is given and the problem to be solved is explained. The conditions for the existence of SM are given in Section 3. The closed-loop reachability condition is given in Section 4. The finite-time convergence conditions are given in Section 5. Simulation example and results are demonstrated in Section 6.
Notation: A standard notation is used throughout the article,  denotes the
denotes the  dimensional Euclidean space with vector norm
dimensional Euclidean space with vector norm 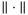 ,
, 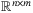 is the set of all
is the set of all 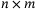 real matrices, and
real matrices, and 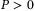 for
for 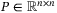 means that P is symmetric and positive definite. The symmetric elements of the symmetric matrix are denoted by
means that P is symmetric and positive definite. The symmetric elements of the symmetric matrix are denoted by  .
. 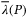 and
and 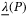 denote the maximum and minimum eigen-value of the matrix P. The symbol
denote the maximum and minimum eigen-value of the matrix P. The symbol 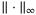 stands for essential supremum. Time dependent variables, such as
stands for essential supremum. Time dependent variables, such as 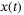 , are simply expressed as x wherever it does (would) not cause any confusion.
, are simply expressed as x wherever it does (would) not cause any confusion. 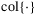 denotes a column vector. Finally,
denotes a column vector. Finally, 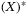 stands for
stands for 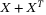 .
.
2 SYSTEM MODELING AND PROBLEM FORMULATION
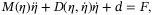 (1)
(1)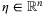 is the generalized position in n axes,
is the generalized position in n axes,  is a time varying positive definite inertia matrix,
is a time varying positive definite inertia matrix, 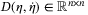 represent the hydraulic damping for autonomous underwater vehicle (AUV),38 the centrifugal and Coriolis force in space manipulators39 or dry friction at each joint in exoskeleton robots.40
represent the hydraulic damping for autonomous underwater vehicle (AUV),38 the centrifugal and Coriolis force in space manipulators39 or dry friction at each joint in exoskeleton robots.40 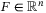 is the generalized control inputs. The term
is the generalized control inputs. The term 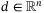 represents any kind of disturbances such as external torques which are assumed to be bounded and
represents any kind of disturbances such as external torques which are assumed to be bounded and 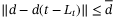 is bounded by a positive constant
is bounded by a positive constant 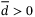 , where
, where 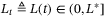 with
with 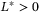 is a known time-varying delay with
is a known time-varying delay with 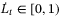 . Matrix
. Matrix 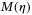 is always positive definite and is invertible. Let
is always positive definite and is invertible. Let 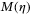 be composed as
be composed as 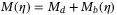 , where
, where 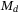 is a diagonal matrix consisting of the constant parameters of the system. Let
is a diagonal matrix consisting of the constant parameters of the system. Let 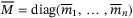 be an user-defined matrix with
be an user-defined matrix with 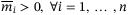 , then system (1) can be written as
, then system (1) can be written as
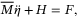 (2)
(2)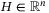 lumps all the nonlinearities and disturbances and is given as
lumps all the nonlinearities and disturbances and is given as
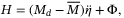 (3)
(3) .
.
Assumption 1.There exist known Lipschitz constants 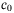 and
and 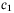 such that
such that
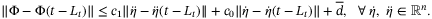 (4)
(4)When we only consider to design a local controller and observer, the assumption of global Lipschitz nonlinearity of 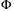 can be replaced by that
can be replaced by that 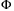 is a local Lipschitz function. All the results given in this note are then valid in a neighborhood around a nominal point. Lipschitz nonlinear systems have been investigated by many authors and some relative works can be found in References 41-43. Since
is a local Lipschitz function. All the results given in this note are then valid in a neighborhood around a nominal point. Lipschitz nonlinear systems have been investigated by many authors and some relative works can be found in References 41-43. Since 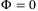 when
when 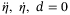 , Assumption 1 implies that there exist constants
, Assumption 1 implies that there exist constants 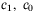 such that
such that 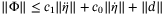 .
.
 , where
, where 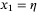 ,
, 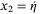 , then (2) can be put into the state-space form
, then (2) can be put into the state-space form
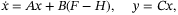 (5)
(5)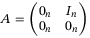 ,
, 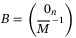 , and
, and 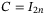 is an identity matrix. Consider the corresponding ideal reference model
is an identity matrix. Consider the corresponding ideal reference model
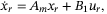 (6)
(6)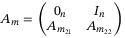 and
and 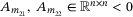 are diagonal matrices. Matrix
are diagonal matrices. Matrix 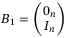 and
and 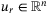 is a command signal. Defining
is a command signal. Defining 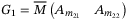 and
and 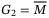 , it yields
, it yields 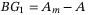 and
and 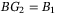 . Next, denoting the error between the ideal reference signals and the system measurements as
. Next, denoting the error between the ideal reference signals and the system measurements as 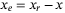 , one can obtain its derivative as
, one can obtain its derivative as
 (7)
(7)In this article, we aim to construct the estimate of H and use this estimate in our control law to increase the robust performance of the closed-loop system subjected to external disturbances. However, the construction of this estimation requires the acceleration signals of system (5), which has the position and velocity signals available only. In the following, a SM observer will be designed to estimate the acceleration signals of the system.
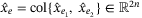 be the observer states, and
be the observer states, and 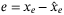 be the observation error. Our control law is defined as
be the observation error. Our control law is defined as
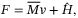 (8)
(8)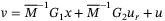 and the expression of
and the expression of 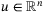 will be given later.
will be given later.  denotes the estimation of H in TDC and is given as
denotes the estimation of H in TDC and is given as
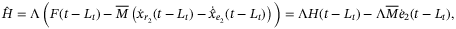 (9)
(9)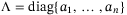 with
with 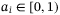 is a positive diagonal matrix which governs the accuracy of the nonlinearity-disturbance estimation. It is assumed
is a positive diagonal matrix which governs the accuracy of the nonlinearity-disturbance estimation. It is assumed 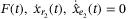 for
for 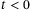 .
.
Remark 1.In practice, the smallest achievable 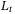 is the minimum sampling period in digital implementation. A digital control system behaves reasonably close to the continuous system if the sampling rate is larger than 30 times the bandwidth.44 Hence, with
is the minimum sampling period in digital implementation. A digital control system behaves reasonably close to the continuous system if the sampling rate is larger than 30 times the bandwidth.44 Hence, with 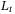 smaller than this level, H is assumed to be continuous and its effect can be estimated as
smaller than this level, H is assumed to be continuous and its effect can be estimated as 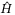 in TDC. For sampled data control, Equation (9) becomes
in TDC. For sampled data control, Equation (9) becomes
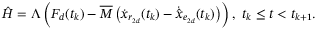 (10)
(10)Following the approach in References 45 and 46, the above equation can be formulated as a continuous-time system with a known delay as in (9), where 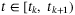 and
and 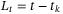 . Sampling may be variable but subject to
. Sampling may be variable but subject to 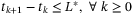 , that is, the time between any two sequential sampling instants is not greater than some pre-chosen
, that is, the time between any two sequential sampling instants is not greater than some pre-chosen 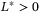 . Then
. Then 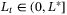 with
with 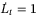 for
for 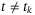 is known with the known sampling instants
is known with the known sampling instants 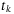 . For control design of a sampled-data system, one could refer to References 45 and 46. The sampled-data control will allow easier implementation of the disturbance estimation (9). Thus TDC observes the states and the inputs of the system one sample into the past at
. For control design of a sampled-data system, one could refer to References 45 and 46. The sampled-data control will allow easier implementation of the disturbance estimation (9). Thus TDC observes the states and the inputs of the system one sample into the past at 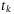 , and determines the control action that should be commanded at time t.
, and determines the control action that should be commanded at time t.
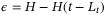 , which is the disturbance and nonlinearity estimation errors, and substituting (9), (11) becomes
, which is the disturbance and nonlinearity estimation errors, and substituting (9), (11) becomes
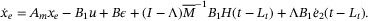 (12)
(12)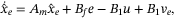 (13)
(13)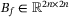 is the observer matrix to be constructed and
is the observer matrix to be constructed and  is the observer control inputs to be designed. Then, denoting
is the observer control inputs to be designed. Then, denoting 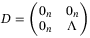 , the observer output error dynamics can be written as follows
, the observer output error dynamics can be written as follows
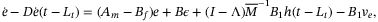 (14)
(14) ,
,  ,
,  . Equation (14) is a time delay system of a neutral type. For more studies on this type of systems please refer to Reference 6 and references therein.
. Equation (14) is a time delay system of a neutral type. For more studies on this type of systems please refer to Reference 6 and references therein.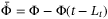 ,
,  , and
, and 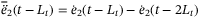 , then it can be shown that
, then it can be shown that
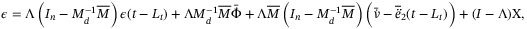 (15)
(15)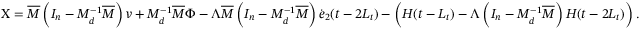 (16)
(16)For the proof of (15), please see Appendix A.1.
Remark 2.Equation (15) can be validated by setting 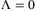 , then
, then  and
and 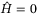 . Since by definition
. Since by definition 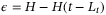 , the following holds:
, the following holds:
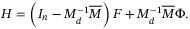 (17)
(17)It is desirable to choose a larger 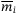 in
in 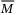 so that the effect of
so that the effect of 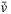 and
and 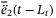 on
on 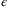 is reduced in (15). However, larger values of
is reduced in (15). However, larger values of 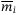 will increase the effect of
will increase the effect of 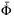 on
on 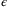 . Since
. Since 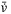 depends on the control signal u and the reference model matrix
depends on the control signal u and the reference model matrix 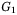 and
and 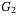 , and
, and 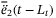 depends on the observer gain
depends on the observer gain 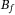 , the choice of the controller and observer gains, as well as the reference signal parameters have a direct impact on TDC error
, the choice of the controller and observer gains, as well as the reference signal parameters have a direct impact on TDC error 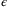 . While we can reduce the values of the diagonal elements in
. While we can reduce the values of the diagonal elements in 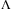 to minimize the dependence of
to minimize the dependence of 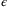 on
on 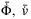 , and
, and 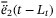 , this causes
, this causes  to depend more on
to depend more on  and the accuracy of disturbance estimation (9) to be degraded. We aim to provide the delay-dependent LMI conditions to assess the trade-off between the performance of disturbance estimation and robust stability and provide the minimum control gains that preserves the performance of TDC.
and the accuracy of disturbance estimation (9) to be degraded. We aim to provide the delay-dependent LMI conditions to assess the trade-off between the performance of disturbance estimation and robust stability and provide the minimum control gains that preserves the performance of TDC.
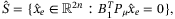 (18)
(18)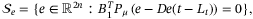 (19)
(19)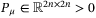 is to be designed. It is desirable to design the estimation of nonlinearities and disturbance (9), the controller (8), the reference model parameters (6) and the observer (13) such that the closed-loop system is exponentially stable and the closed-loop system converges to the sliding surfaces (18) and (19) in finite time.
is to be designed. It is desirable to design the estimation of nonlinearities and disturbance (9), the controller (8), the reference model parameters (6) and the observer (13) such that the closed-loop system is exponentially stable and the closed-loop system converges to the sliding surfaces (18) and (19) in finite time.3 SLIDING MANIFOLDS DESIGN
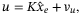 (20)
(20)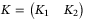 ,
, 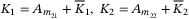 and
and 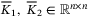 are the control gains to be designed and
are the control gains to be designed and 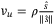 is the nonlinear control law. Let's define the observer matrix
is the nonlinear control law. Let's define the observer matrix 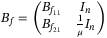 , where
, where 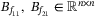 are to be designed. The observer control law is given in the form of
are to be designed. The observer control law is given in the form of
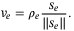 (21)
(21)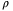 and
and 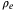 are some positive scalar functions of the outputs. We can write the observer system (13) and the error system (14) in the following form
are some positive scalar functions of the outputs. We can write the observer system (13) and the error system (14) in the following form
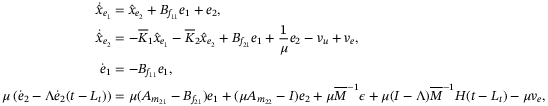 (22)
(22)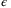 is given in (15). Let
is given in (15). Let 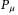 be in the following structure
be in the following structure
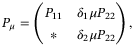 (23)
(23)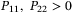 and
and 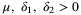 are user-defined parameters. A state transformation exists such that
are user-defined parameters. A state transformation exists such that 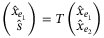 , and
, and 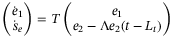 , where
, where 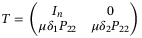 . Hence system (22) can be rewritten as
. Hence system (22) can be rewritten as
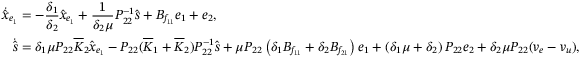 (24)
(24)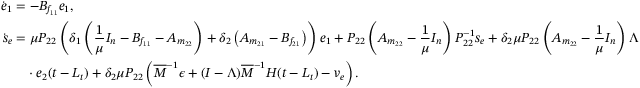 (25)
(25)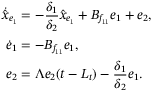 (26)
(26)
Lemma 1.Given positive parameters 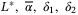 , positive diagonal matrix
, positive diagonal matrix 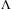 , if there exist
, if there exist 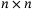 matrices
matrices 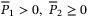 and matrices
and matrices 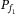 ,
, 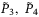 such that the following LMI
such that the following LMI
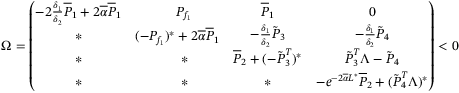 (27)
(27)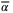 for all
for all 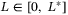 . There exists
. There exists 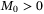 such that the solution of (26) initialized by
such that the solution of (26) initialized by 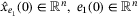 satisfy the following inequality:
satisfy the following inequality:
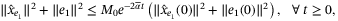 (28)
(28)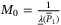 . Moreover, the observer matrix
. Moreover, the observer matrix 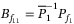 .
.
Proof.Consider the following Lyapunov–Krasovskii functional
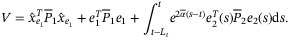 (29)
(29)We define
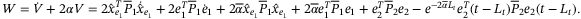 (30)
(30)Then adding
 (31)
(31)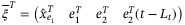 , it follows
, it follows 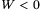 in (30) if
in (30) if 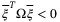 .
. 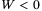 yields the solution of (26) to satisfy the bound
yields the solution of (26) to satisfy the bound 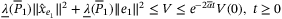 .
.
Remark 3.Lemma 1 provides conditions for the existence of SM for both the observer system and error system with neutral delay in a single LMI (27). Observer-based SMC control for systems with state delays has been studied in Reference 47, and for neutral delay systems has been studied in Reference 48. In those works, LMI conditions for the existence of SM with respect to the observer system were provided separately from the existence design for the observer error system. But the existence conditions related to the observer error dynamics were however missing. Lemma 1 shows that the existence of SM in observer-based SMC can be considered with respect to both the observer system and the error system.
4 REACHABILITY OF THE CLOSED LOOP SYSTEM
This section considers controller and observer design such that the closed-loop system (22) is exponentially attracted to an ultimate bound. Denoting 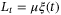 , where
, where 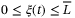 and
and 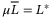 , with
, with 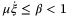 , then the following main result can be stated.
, then the following main result can be stated.
Theorem 1.Given positive tuning diagonal matrix 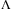 with its elements
with its elements 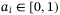 for
for 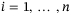 , positive
, positive 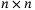 diagonal matrix
diagonal matrix 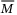 , positive parameters
, positive parameters 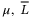 ,
, 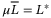 , and positive tuning scalars
, and positive tuning scalars 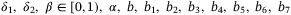 , positive scalars
, positive scalars 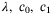 , and scalars
, and scalars 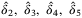 , if there exist a
, if there exist a 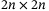 matrix
matrix 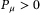 as in (23), and
as in (23), and 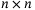 matrices
matrices  ,
, 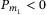 ,
, 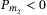 ,
, 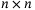 matrices
matrices  ,
, 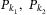 , and
, and 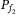 such that LMI
such that LMI 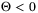 with the following entries:
with the following entries:
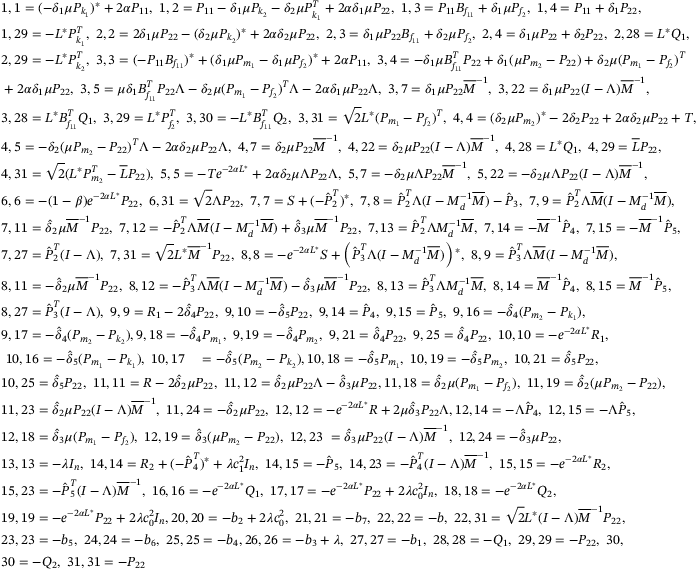 (32)
(32) (33)
(33) for all
for all  ,
, 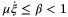 . Moreover, the following matrices can be obtained as
. Moreover, the following matrices can be obtained as 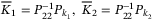 ,
, 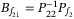 , and
, and 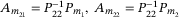 .
.
Proof.See Appendix A.2.
Corollary 1.If there exists 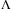 with
with 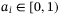 for
for 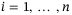 arbitrarily close to 1 such that LMI (32) is feasible, then in the absence of switching controls, that is,
arbitrarily close to 1 such that LMI (32) is feasible, then in the absence of switching controls, that is, 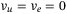 , under constant disturbances
, under constant disturbances 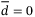 , and
, and 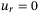 in (6), system (22) is exponentially asymptotically stable with a decay rate
in (6), system (22) is exponentially asymptotically stable with a decay rate 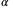 for all
for all 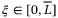 ,
, 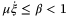 .
.
Proof.Suppose 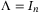 . Then there is no scaling for nonlinearities-disturbance estimation in (9) and
. Then there is no scaling for nonlinearities-disturbance estimation in (9) and 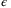 in (15) does not depend on
in (15) does not depend on 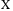 and
and 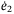 in (22) does not depend on H. The terms on the right-hand side of inequality (33) become
in (22) does not depend on H. The terms on the right-hand side of inequality (33) become 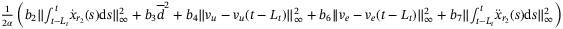 . Setting
. Setting 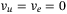 and
and 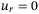 and
and 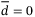 for constant disturbances, the right-hand side of inequality (33) becomes zero as
for constant disturbances, the right-hand side of inequality (33) becomes zero as 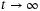 .
.
Remark 4.In Reference 33, an UDE was considered for disturbance cancellation for systems with known input delays. A linear controller without switching parts 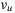 and
and 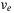 was considered. The uncertainties-disturbance estimation was constructed by delaying the control inputs and measurement signals and then the acceleration signals were estimated using a strictly proper low-pass filter. The disturbance estimation error was shown to be bounded by the system states and the disturbance estimation error itself. A controller was then designed to drive the system without external inputs, that is,
was considered. The uncertainties-disturbance estimation was constructed by delaying the control inputs and measurement signals and then the acceleration signals were estimated using a strictly proper low-pass filter. The disturbance estimation error was shown to be bounded by the system states and the disturbance estimation error itself. A controller was then designed to drive the system without external inputs, that is, 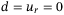 , asymptotically to the origin. Theorem 1 in Reference 33 is an special case of Theorem 1 in this article, which is given by Corollary 1 with
, asymptotically to the origin. Theorem 1 in Reference 33 is an special case of Theorem 1 in this article, which is given by Corollary 1 with 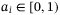 in
in 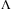 arbitrarily close to 1.
arbitrarily close to 1.
Remark 5.Both system (22) and (15) can be regarded as delay differential-algebraic equations, which have both delay and algebraic constraints. These types of systems often appear in various domains, including aircraft stabilization, chemical engineering systems, lossless transmission lines. In Reference 49, transforming such systems into a descriptor form has been considered and an LMI based stability criterion has been derived. The use of delay for stabilization, in our case for disturbance estimation, extends to other applications. For instance, a known delay is deliberately introduced for a SMC static control design.50 Transformation of algebraic equations with time delay into neutral type system equations, for stability control using artificial delay has been considered in References 3 and 4.
It is shown in Reference 46 that a very small 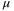 can be chosen to minimize the effect of the sampled-data measurement on observer error, effectively resulting in a singularly perturbed system with respect to the error dynamics. A high-gain observer design was proposed in Reference 51 based on separation principle, that is, designs of the controller and the observer are performed separately and then an output feedback controller is obtained by replacing the states by their estimates provided by the high-gain observer. It is well known that in the observer-based controller design, it is not possible to choose a very small
can be chosen to minimize the effect of the sampled-data measurement on observer error, effectively resulting in a singularly perturbed system with respect to the error dynamics. A high-gain observer design was proposed in Reference 51 based on separation principle, that is, designs of the controller and the observer are performed separately and then an output feedback controller is obtained by replacing the states by their estimates provided by the high-gain observer. It is well known that in the observer-based controller design, it is not possible to choose a very small 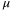 for the system considered as the observer dynamics depends on the inverse of
for the system considered as the observer dynamics depends on the inverse of 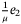 .
.
5 FINITE-TIME CONVERGENCE
Since the closed loop system (22) is ultimately bounded by (33), and by the definition of 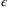 in (15), definitions of
in (15), definitions of 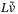 ,
, 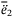 in (A10) and (A13), respectively, there exists a
in (A10) and (A13), respectively, there exists a 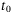 such that
such that 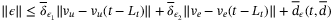 , where
, where 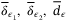 are some positive constants for all
are some positive constants for all 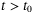 . Also we have
. Also we have 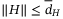 , where
, where 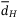 is a positive constant for all
is a positive constant for all 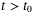 .
.
Corollary 2.Given positive constants  , and
, and  , for any positive numbers
, for any positive numbers 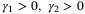 , then the following switching gains
, then the following switching gains
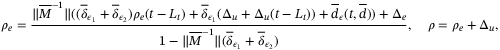 (34)
(34)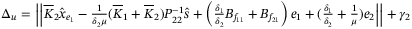 and
and
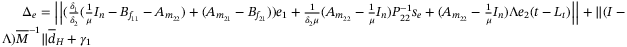 , will ensure ideal sliding motions are attained on (18) and (19) in finite time.
, will ensure ideal sliding motions are attained on (18) and (19) in finite time.
Proof.Let 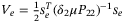 , then
, then 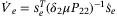 . Substituting
. Substituting 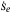 in (25) and then
in (25) and then  in (34) gives
in (34) gives
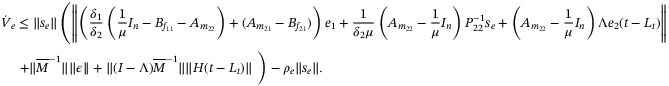 (35)
(35)Rearranging (34) yields
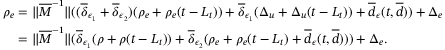 (36)
(36)Since 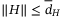 , we also have
, we also have 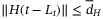 for all
for all 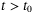 . Substituting (36) into (35), we have
. Substituting (36) into (35), we have 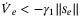 . Next, let
. Next, let 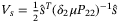 , then substituting
, then substituting 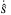 in (24)
in (24)
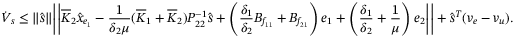 (37)
(37)Since we have shown 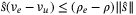 in (A16), substituting
in (A16), substituting 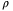 in (34) yields
in (34) yields 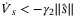 . Thus sliding motions will be attained in finite time.
. Thus sliding motions will be attained in finite time.
Remark 6.The switching gain 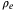 in (34) depends on
in (34) depends on 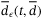 , where
, where 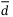 defines the bound on
defines the bound on 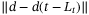 , this allows a smaller
, this allows a smaller 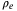 to be chosen. It shows the advantage of using disturbance estimation (in our case, TDC) based SMC as in conventional SMC without using disturbance estimation technique, the switching gain needs to be large enough to attenuate the effect of the disturbance
to be chosen. It shows the advantage of using disturbance estimation (in our case, TDC) based SMC as in conventional SMC without using disturbance estimation technique, the switching gain needs to be large enough to attenuate the effect of the disturbance 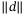 . Smaller switching gain is beneficial in reducing chattering when there is a delay in the control action.28 Compared to TDC, in DO and UDE based control the filter gain design in disturbance estimation requires a priori knowledge of the upper bound of the disturbances
. Smaller switching gain is beneficial in reducing chattering when there is a delay in the control action.28 Compared to TDC, in DO and UDE based control the filter gain design in disturbance estimation requires a priori knowledge of the upper bound of the disturbances 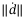 , which is hard to estimate and its bound can be much larger for unknown disturbances.15, 16, 30, 33 The clear advantage of TDC based disturbance estimation over DO and UDE is that the disturbance estimation error only depends on
, which is hard to estimate and its bound can be much larger for unknown disturbances.15, 16, 30, 33 The clear advantage of TDC based disturbance estimation over DO and UDE is that the disturbance estimation error only depends on 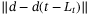 , whose upper bound is much smaller than
, whose upper bound is much smaller than 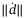 .
.
5.1 Design procedure
- Select the maximum delay size
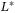 . In digital control, the smallest delay achievable is a sample period. Select the set of parameters
. In digital control, the smallest delay achievable is a sample period. Select the set of parameters 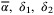 and the diagonal matrix
and the diagonal matrix 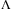 such that LMI (27) is feasible. Larger values of
such that LMI (27) is feasible. Larger values of 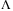 is preferred.
is preferred. - Determine the values of
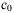 and
and 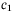 such that the bound (4) holds. Using larger values for larger
such that the bound (4) holds. Using larger values for larger 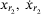 . They can be chosen zero for a constant speed tracking.
. They can be chosen zero for a constant speed tracking. - Select
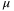 such that we can increase
such that we can increase 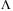 . Ideally a smaller
. Ideally a smaller 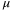 is preferable, but
is preferable, but 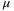 needs to be large enough as the feasibility of LMI (32) depends on a large enough
needs to be large enough as the feasibility of LMI (32) depends on a large enough 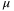 .
. - Then choose a larger
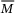 as close to
as close to 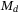 as possible.
as possible. - Reduce
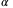 for larger values of
for larger values of 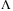 . Then reduce values for
. Then reduce values for 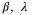 , b,
, b, 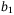 ,
, 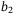 ,
, 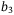 ,
, 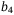 ,
, 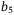 ,
, 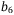 ,
, 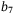 such that LMI (32) is still feasible. Tuning parameters
such that LMI (32) is still feasible. Tuning parameters 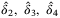 , and
, and 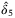 can be chosen as small values to start with.
can be chosen as small values to start with.
6 SIMULATION RESULTS
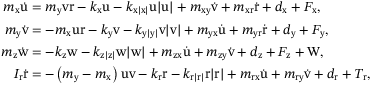 (38)
(38)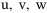 in
in  are the linear velocities in the surge, sway, and heave, respectively,
are the linear velocities in the surge, sway, and heave, respectively, 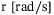 is the angular velocity in the yaw. The surge and sway motions are usually coupled with the yaw motion. Mass values
is the angular velocity in the yaw. The surge and sway motions are usually coupled with the yaw motion. Mass values 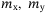 ,
, 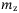 ,
, 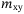 ,
, 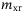 ,
, 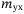 ,
, 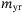 ,
, 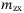 ,
, 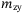 ,
, 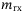 ,
, 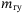 , in
, in  stand for the masses that include both the rigid body mass and the added mass due to the surrounding fluid in the surge, sway, and heave;
stand for the masses that include both the rigid body mass and the added mass due to the surrounding fluid in the surge, sway, and heave; 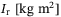 is the moment of inertia in the yaw (including added mass and inertia);
is the moment of inertia in the yaw (including added mass and inertia); 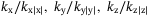 , and
, and 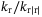 are the linear/quadratic damping coefficients in the surge, sway, heave, and yaw, respectively.
are the linear/quadratic damping coefficients in the surge, sway, heave, and yaw, respectively. 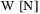 is the resultant weight accounting for the buoyancy force in heave, and finally
is the resultant weight accounting for the buoyancy force in heave, and finally 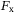 ,
, 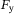 ,
, 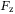 in
in 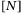 and
and 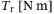 are the control inputs.
are the control inputs.Considering underwater vehicle control in proximity to sub-sea structures, a vehicle is expected to respond quickly to locally generated flow disturbances while maintaining a stable position relative to a static or moving structure. The oscillation of the structure due to water flow generates local eddies and turbulence flow around the structure and the vehicle in close proximity to the structure. This makes the stable positioning of the vehicle relative to the moving structure rather challenging. In order to improve the robust performance under unavoidable and unknown disturbance, a SMC-based control is considered for its intrinsic robust property. The actuators of the AUV are thrusters whose rotational switching frequency (able to switch rotational direction every haft second) is relatively much faster compared to the reacting motion of the vehicle in the water. For sake of simplicity and space, we only show simulation results for surge, sway, and yaw motions and not for heave motion. The parameters of the physical model of the AUV that we consider are provided in Table 1.53
| Cyclops parameter | Value |
|---|---|
| Rigid body mass of Cyclops, m (kg) | 219.8 |
Mass of Cyclops in surge, 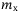 (kg) (kg) |
391.5 |
Linear drag coefficient in surge, 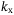 |
120 |
Quadratic drag coefficient in surge, 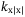 |
229.4 |
Mass of Cyclops in sway, 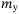 (kg) (kg) |
639.6 |
Linear drag coefficient in sway,  |
131.8 |
Quadratic drag coefficient in sway, 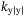 |
328.3 |
Inertia of Cyclops in yaw, 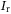 (kg m (kg m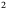 ) ) |
130 |
Linear drag coefficient in yaw, 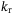 |
80 |
Quadratic drag coefficient in yaw, 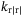 |
280 |
Other mass values, 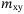 , , 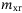 , , 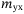 , , 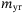 (kg) (kg) |
4, 7, 7, 29 |
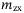 , , 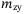 , , 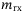 , , 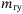 (kg) (kg) |
15, 25, 7, 20 |
To demonstrate the effectiveness of the method, we consider two cases. In case 1, we consider the vehicle to follow a constant speed reference. In case 2, we consider the vehicle to follow a variable speed reference.
For constant speed tracking, we can choose 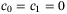 in (4) as
in (4) as  . We have chosen a constant delay of 0.1 s. This represents the simplest case to investigate the best performance that we can obtain from the proposed control strategy. In LMI (27), choosing
. We have chosen a constant delay of 0.1 s. This represents the simplest case to investigate the best performance that we can obtain from the proposed control strategy. In LMI (27), choosing 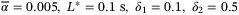 , and
, and 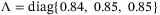 , we obtain the observer matrix
, we obtain the observer matrix 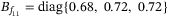 . In LMI (32), choosing
. In LMI (32), choosing 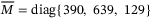 ,
, 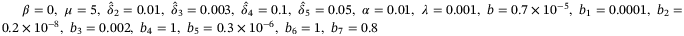 , we obtain the reference model, controller and observer matrices as
, we obtain the reference model, controller and observer matrices as 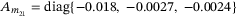 ,
, 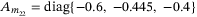 ,
, 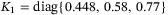 ,
, 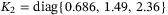 ,
, 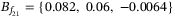 . The Lyapunov matrix is
. The Lyapunov matrix is 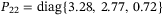 and
and 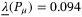 . In the switching gain design in (34), we choose
. In the switching gain design in (34), we choose 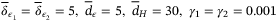 .
.
For the varying speed tracking, we choose 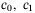 such that
such that 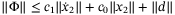 , as implied by Assumption 1. By definition, we have
, as implied by Assumption 1. By definition, we have 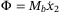
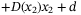 , where
, where 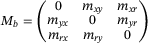 and
and 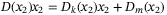 in system (38), with
in system (38), with 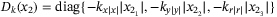 ,
, 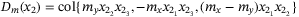 and
and 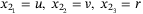 . We assume that the velocities
. We assume that the velocities 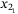 ,
, 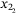 ,
, 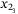 are small such that the following bound
are small such that the following bound 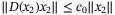 holds, where
holds, where 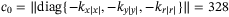 . We choose
. We choose 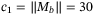 . In LMI (27), we select
. In LMI (27), we select 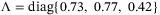 and keep the other parameters the same as those in the case of constant speed tracking. We obtain
and keep the other parameters the same as those in the case of constant speed tracking. We obtain 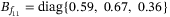 . In LMI (32), we choose
. In LMI (32), we choose 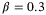 ,
, 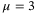 ,
, 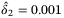 ,
, 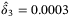 ,
, 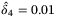 ,
, 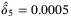 ,
, 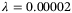 ,
, 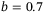 ,
, 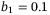 ,
, 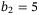 ,
, 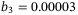 ,
, 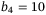 ,
, 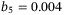 ,
, 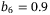 ,
, 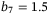 and keep
and keep 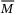 ,
, 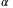 the same as chosen in the case of constant speed. We obtain the reference model, controller and observer matrices as
the same as chosen in the case of constant speed. We obtain the reference model, controller and observer matrices as 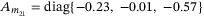 ,
, 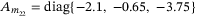 ,
, 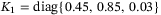 ,
, 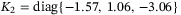 ,
, 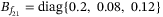 . The Lyapunov matrix is
. The Lyapunov matrix is 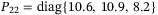 and
and 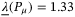 . For the switching gain design, we keep
. For the switching gain design, we keep 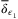 ,
, 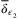 ,
, 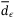 ,
, 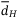 ,
, 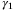 ,
, 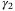 the same as in the case of constant speed design.
the same as in the case of constant speed design.
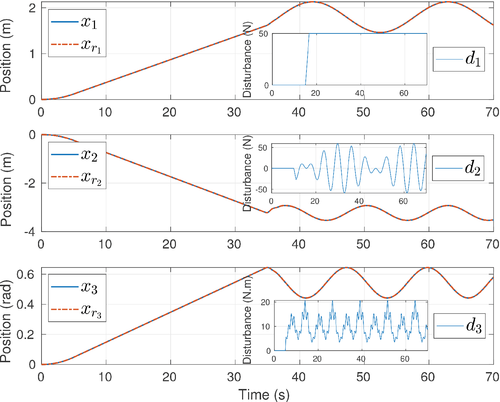
In the simulation, we consider constant speed tracking in the first 35 s and variable speed tracking afterwards, as shown in Figure 1. The figure shows that the tracking performance was maintained in the presence of disturbances in surge, sway, and yaw. The delay 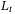 is constant during the constant speed tracking and becomes variable with a rate less than 0.3 afterwards (Figure 2). The TDC input
is constant during the constant speed tracking and becomes variable with a rate less than 0.3 afterwards (Figure 2). The TDC input 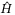 is plotted in comparison to the actual nonlinearity and disturbance signals H in Figure 3. It can be seen that the estimation
is plotted in comparison to the actual nonlinearity and disturbance signals H in Figure 3. It can be seen that the estimation 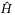 is in an approximate neighborhood of the actual H in surge and sway. In yaw, the estimation
is in an approximate neighborhood of the actual H in surge and sway. In yaw, the estimation 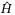 is quite close to the actual H during constant speed tracking but its estimation accuracy deteriorates during variable speed tracking as the scaling factor
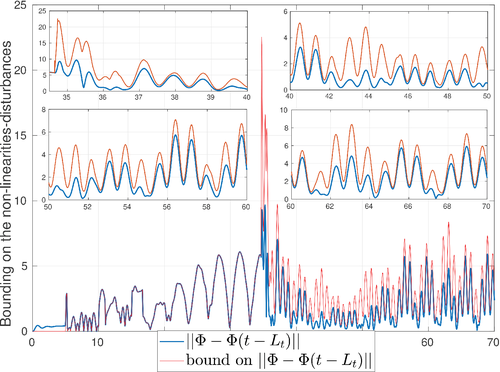
is quite close to the actual H during constant speed tracking but its estimation accuracy deteriorates during variable speed tracking as the scaling factor 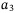 is reduced from 0.85 to 0.42. Figure 4 shows that during constant speed tracking, as
is reduced from 0.85 to 0.42. Figure 4 shows that during constant speed tracking, as  , we have
, we have 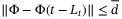 in (4). Note that in the first 5 s, the condition
in (4). Note that in the first 5 s, the condition 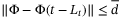 does not hold since the vehicle's speed increases in the interval
does not hold since the vehicle's speed increases in the interval 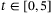 s, when its speed stays unchanged thereafter. In the meantime,
s, when its speed stays unchanged thereafter. In the meantime, 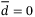 in the first 5 s as seen in the zoom-in plots in Figure 1. During variable speed tracking, the zoom-in plots in Figure 4
show
in the first 5 s as seen in the zoom-in plots in Figure 1. During variable speed tracking, the zoom-in plots in Figure 4
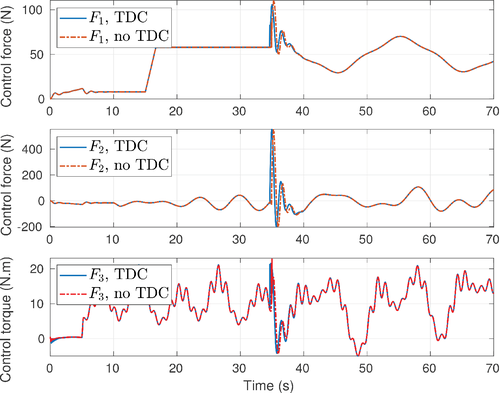
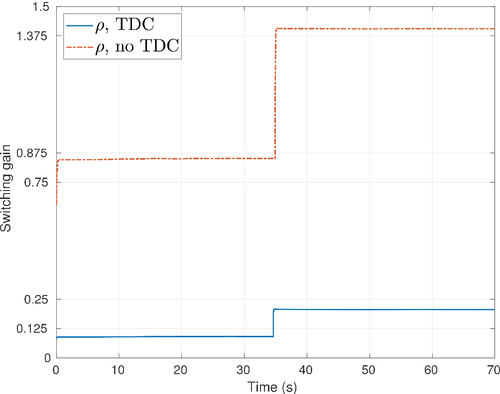
show 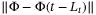 is always bounded by the right-hand side of (4). Figures 5-7 show the sliding surface, control inputs, and the switching gain in TDC (blue line in the figures).
is always bounded by the right-hand side of (4). Figures 5-7 show the sliding surface, control inputs, and the switching gain in TDC (blue line in the figures).
 in TDC is constant and then become variable
in TDC is constant and then become variable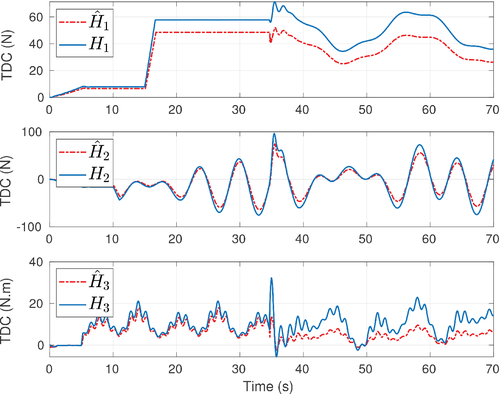
 in Equation (4)
in Equation (4)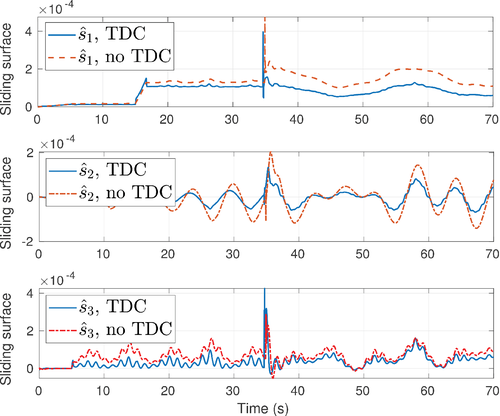
 ) with comparison to non-TDC (without
) with comparison to non-TDC (without  )
)
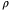 used in TDC and non-TDC
used in TDC and non-TDCBelow we demonstrate the effectiveness of TDC (with 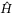 ) in reducing the potential chattering caused by larger switching energy in SMC. We replace
) in reducing the potential chattering caused by larger switching energy in SMC. We replace 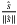 ,
, 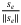 in
in 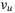 and
and 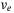 with
with 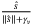 and
and 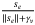 , respectively, where
, respectively, where 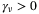 is a small constant. This allows smoothing the discontinuity in the nonlinear switching control in SMC to obtain an arbitrarily close but continuous approximation of the discontinuous functions. This approximation is reasonable as the thrusters in an AUV change rotational speed and directions continuously.
is a small constant. This allows smoothing the discontinuity in the nonlinear switching control in SMC to obtain an arbitrarily close but continuous approximation of the discontinuous functions. This approximation is reasonable as the thrusters in an AUV change rotational speed and directions continuously.
In Figure 5, the sliding surface using TDC (with 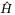 ) and without using TDC (without
) and without using TDC (without 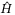 ) in surge, sway, and yaw are shown to be in the similar magnitudes. The control inputs are shown in Figure 6. It is seen in both cases that the same level of control inputs are present to keep the sliding surface
) in surge, sway, and yaw are shown to be in the similar magnitudes. The control inputs are shown in Figure 6. It is seen in both cases that the same level of control inputs are present to keep the sliding surface 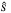 at the same level. However, the result of not using TDC requires larger switching gain
at the same level. However, the result of not using TDC requires larger switching gain 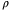 , Figure 7. The value of
, Figure 7. The value of 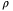 in non-TDC case is about 8 times larger than that in the TDC case. The smaller switching gain due to TDC (using
in non-TDC case is about 8 times larger than that in the TDC case. The smaller switching gain due to TDC (using 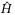 to compensate for the effect of the actual nonlinear-disturbance H rather than using larger switching gain) reduces the risk of potential chattering due to the switching control action. In both of the controllers, TDC or non-TDC, the switching gain
to compensate for the effect of the actual nonlinear-disturbance H rather than using larger switching gain) reduces the risk of potential chattering due to the switching control action. In both of the controllers, TDC or non-TDC, the switching gain 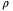 is increased from constant speed tracking to variable speed tracking due to the decreased value of
is increased from constant speed tracking to variable speed tracking due to the decreased value of 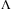 in TDC and larger value of H in variable speed tracking. The effect of delay size on the scaling factor
in TDC and larger value of H in variable speed tracking. The effect of delay size on the scaling factor 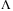 can be seen in Figure 8. The data in the figure is obtained by setting
can be seen in Figure 8. The data in the figure is obtained by setting 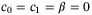 in the LMI (27) and (32). It is shown that the scaling factor
in the LMI (27) and (32). It is shown that the scaling factor 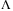 needs to be reduced for increasing delay size
needs to be reduced for increasing delay size  , weakening the efficiency of TDC in compensating the nonlinearity-disturbances.
, weakening the efficiency of TDC in compensating the nonlinearity-disturbances.
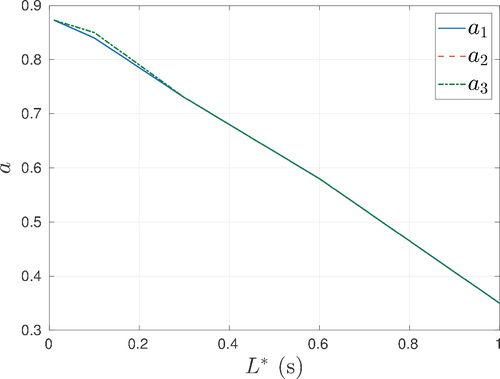
 against scaling factor
against scaling factor  in
in 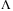
In this section, we have demonstrated that the effectiveness of using TDC in reducing the potential chattering in SMC, by compensating the nonlinearity-disturbance with its estimate from the past control and measurement information. In constant speed tracking, the estimation accuracy of nonlinearity-disturbance is higher compared to variable speed tracking. It is seen that in TDC, the level of compensation for H by 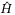 is affected by the design parameter
is affected by the design parameter 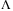 . We have shown that the maximum value we can achieve for
. We have shown that the maximum value we can achieve for 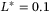 s is
s is 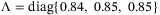 , which is obtained at constant speed tracking with a constant delay. Note that
, which is obtained at constant speed tracking with a constant delay. Note that 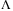 needs to be chosen by considering the size of the delay, controller gains, observer gains and the reference model parameters to maximize the TDC performance and to avoid potential instability.
needs to be chosen by considering the size of the delay, controller gains, observer gains and the reference model parameters to maximize the TDC performance and to avoid potential instability.
7 CONCLUSION
TDC is a simple but effective disturbance observation based control technique. However, it suffers from that it requires all system states to be available including the acceleration measurement which is not easily accessible in many physical systems. There is still a lack of analytical tools to find the limitations of this approach and to analyze the trade of between robust stability and performance for a designed TDC. In this article, a SM observer has been designed to circumvent the need for acceleration measurement that has been commonly assumed available in TDC. The resulting observer error system is shown to be a time delay system of neutral type. A tuning factor 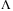 is introduced for TDC-based nonlinearities-disturbance estimation, which governs the accuracy of the non-linearity-disturbance estimation and the robust performance of TDC. Delay-dependent linear matrix inequalities (LMIs) conditions are proposed for the design of TDC with the SM. The size of the delay, the controller gains, the observer gains, and the reference model parameters are determined from the LMIs which minimize the ultimate bound of the closed-loop system. It is shown with simulations that higher estimation accuracy can be achieved for a constant speed tracking than varying speed tracking. The advantage of using TDC is demonstrated with the simulation results as the substitution of the nonlinearity-disturbance estimation (TDC) in the control law compensate for the effect of the actual nonlinearities and disturbance and the resulting closed-loop system is constrained into a smaller neighborhood of the origin. As a consequence a smaller switching gain can be designed in SMC to induce a SM. The smaller switching gain reduces the potential undesirable chattering caused by the switching control action. It is shown that for larger delay size the scaling factor
is introduced for TDC-based nonlinearities-disturbance estimation, which governs the accuracy of the non-linearity-disturbance estimation and the robust performance of TDC. Delay-dependent linear matrix inequalities (LMIs) conditions are proposed for the design of TDC with the SM. The size of the delay, the controller gains, the observer gains, and the reference model parameters are determined from the LMIs which minimize the ultimate bound of the closed-loop system. It is shown with simulations that higher estimation accuracy can be achieved for a constant speed tracking than varying speed tracking. The advantage of using TDC is demonstrated with the simulation results as the substitution of the nonlinearity-disturbance estimation (TDC) in the control law compensate for the effect of the actual nonlinearities and disturbance and the resulting closed-loop system is constrained into a smaller neighborhood of the origin. As a consequence a smaller switching gain can be designed in SMC to induce a SM. The smaller switching gain reduces the potential undesirable chattering caused by the switching control action. It is shown that for larger delay size the scaling factor 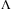 needs to be reduced.
needs to be reduced.
ACKNOWLEDGMENTS
This research has been funded by the Engineering and Physical Sciences Research Council of the United Kingdom (EPSRC) through the Offshore Robotics for Certification of Assets (ORCA) Hub—Partnership Resource Fund for ROBMAN Project, under grant reference EP/R026173/1.
We owe a debt of gratitude to Professor Emilia Fridman for the insightful discussion which improves our main results.
CONFLICT OF INTEREST
The authors declare no potential conflict of interests.
APPENDIX A
A.1 Proof of Equation (15)
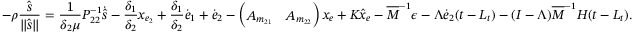 (A4)
(A4)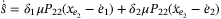 into the above equation, we achieve
into the above equation, we achieve
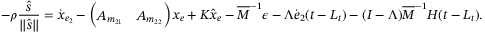 (A5)
(A5)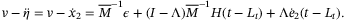 (A6)
(A6)A.2 Proof of Theorem 1
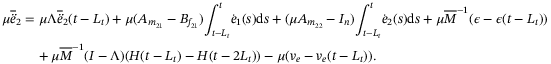 (A13)
(A13)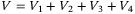 for the observer and the error dynamics in (22), as below:
for the observer and the error dynamics in (22), as below:
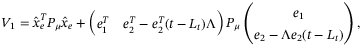
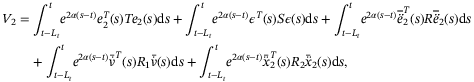
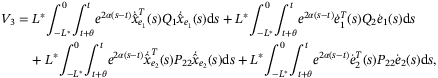
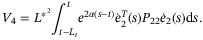 (A14)
(A14)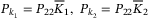 ,
, 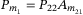 ,
, 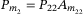 , and
, and 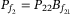 , and differentiating
, and differentiating 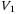 yields
yields
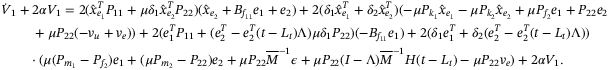 (A15)
(A15)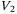 yields
yields
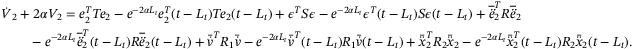 (A18)
(A18)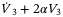 , we first consider the first term and denote
, we first consider the first term and denote 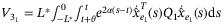 , then it follows that
, then it follows that
 (A19)
(A19) (A20)
(A20)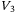 , Jensen's inequality can be applied to the similar terms in the same way. Using Schur complement for the following terms yields
, Jensen's inequality can be applied to the similar terms in the same way. Using Schur complement for the following terms yields
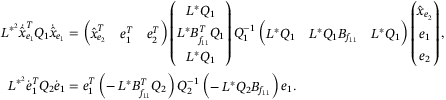 (A21)
(A21) and
and 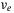 terms in (A16) and (A17) are control signals rather than disturbance, we can analyze the linear part of
terms in (A16) and (A17) are control signals rather than disturbance, we can analyze the linear part of 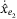 and
and 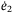 when writing their Schur complement as follows:
when writing their Schur complement as follows:
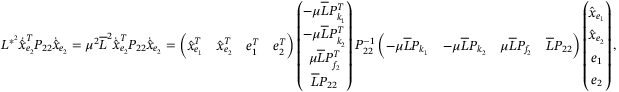 (A22)
(A22)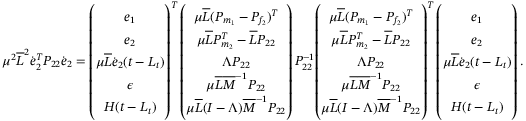 (A23)
(A23)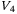 yields
yields
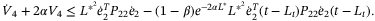 (A24)
(A24)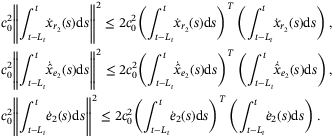 (A26)
(A26)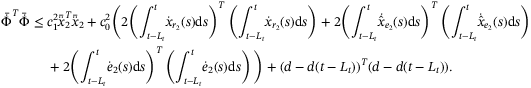 (A27)
(A27)Open Research
DATA AVAILABILITY STATEMENT
This article describes entirely theoretical research. Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.



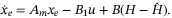
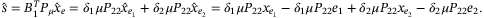
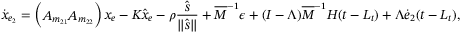
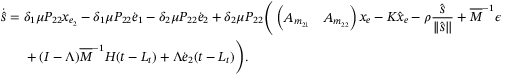
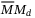 and substituting
and substituting 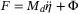 , we have
, we have
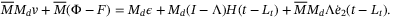
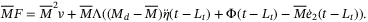
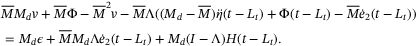
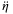 from (
from (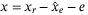 , it follows that
, it follows that
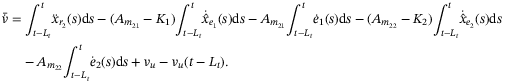

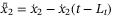 , we get
, we get
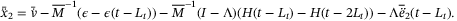
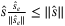 , it follows in (
, it follows in (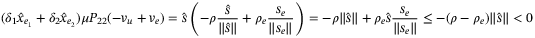
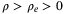 , and
, and

 and
and 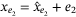 , we can write
, we can write
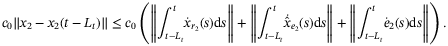
 -procedure,
-procedure,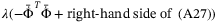 , where
, where 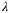 is any positive number, is added to the following
is any positive number, is added to the following
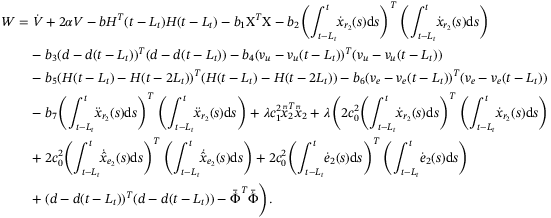

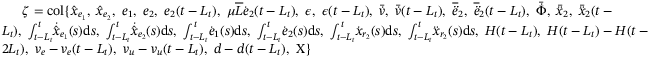 , then
, then  is satisfied if
is satisfied if 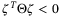 , which is nothing but
, which is nothing but 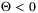 , where
, where 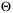 is explicitly given in (
is explicitly given in ( Francis;
Francis;