Structural relaxation of stacked ultrathin polystyrene films
Abstract
The Tg depression and kinetic behavior of stacked polystyrene ultrathin films is investigated by differential scanning calorimetry (DSC) and compared with the behavior of bulk polystyrene. The fictive temperature (Tf) was measured as a function of cooling rate and as a function of aging time for aging temperatures below the nominal glass transition temperature (Tg). The stacked ultrathin films show enthalpy overshoots in DSC heating scans which are reduced in height but occur over a broader temperature range relative to the bulk response for a given change in fictive temperature. The cooling rate dependence of the limiting fictive temperature, Tf′, is also found to be higher for the stacked ultrathin film samples; the result is that the magnitude of the Tg depression between the ultrathin film sample and the bulk is inversely related to the cooling rate. We also find that the rate of physical aging of the stacked ultrathin films is comparable with the bulk when aging is performed at the same distance from Tg; however, when conducted at the same aging temperature, the ultrathin film samples show accelerated physical aging, that is, a shorter time is required to reach equilibrium for the thin films due to their depressed Tg values. The smaller distance from Tg also results in a reduced logarithmic aging rate for the thin films compared with the bulk, although this is not indicative of longer relaxation times. The DSC heating curves obtained as a function of cooling rate and aging history are modeled using the Tool-Narayanaswamy-Moynihan model of structural recovery; the stacked ultrathin film samples show lower β values than the bulk, consistent with a broader distribution of relaxation times. © 2008 Wiley Periodicals, Inc. J Polym Sci Part B: Polym Phys 46: 2741–2753, 2008
INTRODUCTION
The effects of nanoconfinement on the glass transition phenomena of polymer materials have been extensively investigated, and several review articles have been recently written.1-3 Although the experimental results in the literature seem to depend on the measurement technique and material studied, it is generally accepted that the glass transition temperature (Tg) of polymer ultrathin films is depressed relative to the bulk unless strong interactions with a substrate are present. For example, both supported and unsupported (free standing) polystyrene ultrathin films show a noticeable Tg depression relative to that of the bulk state.4-23 For polystyrene, the magnitude of depression can be as great as 70 °C in freely standing ultrathin films.6 In addition, Ellison and Torkelson's work9 on labeled layers in supported polystyrene films shows that there is a gradient in the Tg depression with a greater depression at the surface and only a small depression at the polystyrene/glass substrate interface.
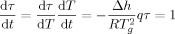 (1)
(1)The time scale of measurement has been also shown to influence the magnitude of the Tg depression at the nanoscale because the dependence of Tg on the time scale of measurement (i.e., the effective activation energy) differs between bulk and nanoscale materials. Schonhals et al.26 reported that the average relaxation time as measured by dielectric spectroscopy in nanopore-confined poly(methyl phenyl siloxane) (PMPS) has a weaker temperature dependence than the bulk, with the slope of log τ versus temperature decreasing to ∼15% of the bulk at 2.5 nm nanopore confinement. As a result, the average relaxation time is reduced significantly under nanopore confinement at lower temperatures, whereas at higher temperatures, the relaxation time is greater for the nanoconfined material. On the other hand, Fakhraai and Forrest7 found that the Tg depression is inversely proportional to the cooling rate, and the Tg of the ultrathin films approaches that of the bulk at a cooling rate of 130 K/min in supported polystyrene ultrathin films. Both Schonhals' and Fakhraai's works7, 26 reveal that the timescale of measurement influences the magnitude of Tg depression, perhaps explaining why no discernable Tg depressions were found in nanocalorimetry18, 19 and AC calorimetry studies20 for polystyrene films as thin as 3 nm due to the high cooling rates and the high frequencies used in those studies.
In addition to affecting the dynamics of the glass transition, nanoconfinement also is expected to influence the kinetics of structural relaxation in the glassy state. However, the effects of the nanoconfinement on physical aging have not been well studied, and some of the results are seemingly contradictory.21, 22, 27-29 Both acceleration and retardation of structural relaxation during physical aging were reported for different types of nanoconfinement and materials. Acceleration is observed for small molecules confined in nanopores because the equilibrium state below Tg differs under this type of nanoconfinement due to isochoric vitrification resulting in smaller relaxation times at temperatures a given distance below Tg.27 In contrast, physical aging is observed to be slower in PMMA ultrathin films compared with the bulk presumably because attractive interactions between the ester groups of PMMA and the hydroxyl group of the silica substrate restrict physical aging of PMMA ultrathin films supported on silica substrate.28 On the other hand, the rate of aging of a 20 nm polystyrene ultrathin film is suggested to be similar to that of the bulk far below Tg for aging times up to 80 min, whereas at an aging temperature just below the bulk Tg, the thin film does not age because it is in the equilibrium state due to its Tg depression.29 Other early work on aging of polystyrene ultrathin films showed depressed enthalpy overshoots compared with bulk, but the aging rates were not quantified.21 In addition to the aging behaviors of ultrathin films, the aging of submicron thin films of polysulfone and poly(2,6-dimethyl-1,4-phenylene oxide) was investigated for aging times of more than 200 days at aging temperature more than 130 °C below Tg using gas permeability and refractive index.30, 31 The aging rate of the thin films (in terms of the slope of log permeability versus log t) increases with decreasing film thickness and with increasing aging temperature in spite of the fact that the Tgs of the submicron-thick thin films are unchanged from the bulk.31
The dynamics and Tg depression in polymer ultrathin films have also been suggested to be related to those in polymer nanocomposites.32, 33 Although nanocomposites differ from supported ultrathin films in that their confinement may be three-dimensional and due to presence of multiparticle interactions, the effects of film thickness and interparticle spacing on Tg have been related.32, 33 Hence, the physical aging of nanocomposites may also be similar to that of the ultrathin films. Unlike ultrathin films, the physical aging of nanocomposites, especially for thermosetting resins, has been more extensively investigated.34-38 The studies of physical aging of nanocomposites have focused on the type of nanofiller, such as silica nanoparticle, graphitic nanofiber, and polyhedral oligosilsesquioxane (POSS), because strong interactions between nanofiller and the thermosetting resin appear to restrict physical aging.34 Similarly, in the case of ultrathin films, interfacial interactions may be an important factor for their physical aging behavior.
In our previous work, the Tg depression and absolute heat capacity of stacked ultrathin polystyrene film samples were reported.23 The advantage of using stacked ultrathin films to study nanoconfinement and intrinsic size effects is that the films do not have free surfaces after annealing above Tg but rather are assumed to have neutral polystyrene–polystyrene interfaces. Multilayer films were also made by Ellison and Torkelson9 to investigate how the Tg of a thin layer depended on its location in the film (e.g., at the surface, substrate, or in the interior of the film) and how it depended on the chemical structure of the adjoining layers.39 The interior layer was found to exhibit a bulk-like Tg when both over and under layers had bulk-like thicknesses, whereas for bilayer and trilayer films composed of two or three ultrathin films, Tg depressions were observed although in the trilayer film, the depression was greater at the surface and weaker at the substrate.9 The results of the bilayer and trilayer stacks of ultrathin films showed that a gradient in Tg exists. Moreover, it was suggested that the average Tg in the bilayer and trilayer ultrathin film stacks was similar to that displayed by single films having the same total thicknesses—thus, suggesting that a stack of ultrathin films should show bulk Tg behavior if the stack is thick enough. This is contrary, however, to our observation that stacked ultrathin film samples containing more than 200 ultrathin films show Tg depressions of similar magnitude to those observed for supported thin films.23 Our results are not inconsistent, though, with Torkelson et al.'s observation that the Tg of a layer depends on the Tg of the layers around it—in our case, these layers are all ultrathin films seemingly with the same depressed Tgs such that the Tg measured is that of a single layer with no free surface and neutral interactions.
It is important to note that the polystyrene used in our stacked samples is ultrahigh molecular weight in order that diffusion between layers cannot occur in the time scale of the experiments such that each film in the stack retains its ultrathin film character; in fact, when interlayer diffusion is allowed to occur (with annealing at high temperature in a press), Tg reverts back to the bulk value as would be expected.23 In our previous work, we not only found a Tg depression similar to that reported for supported polystyrene films,4, 5 but in addition, we found a decrease in the absolute heat capacity in both liquid and glassy regions at the nanoscale. The step in heat capacity at Tg, ΔCp, was also found to decrease with decreasing film thickness. Here, we add to our previous results and extend the study to measure the calorimetric glass transition temperature of the stacked polystyrene ultrathin films as a function of cooling rate and to investigate the physical aging behavior of the ultrathin film samples. In addition to examining the kinetics associated with Tg in these samples, the Tool-Narayanswamy-Moynihan (TNM) model of structural recovery40-42 is employed to allow the quantitative comparison and physical interpretation of the results. The TNM model is widely used to describe the glass transition kinetics of glass-forming materials24, 43-47 even though it is known to have shortcomings.24, 48 In this work, we will use it to help us quantify differences in the nonexponentiality and nonlinearity, by the parameters of β and x, in the ultrathin film and bulk samples.
METHODOLOGY
Sample Preparation
The polystyrene used in this study, obtained from Sigma-Aldrich, has a number–average molecular weight of 1,998,000 g/mol and a molecular weight distribution of 1.02. The radius of gyration (Rg) is 38.7 nm.49 Polystyrene ultrathin films were deposited by spin coating polystyrene dissolved in toluene (HPLC-grade; Sigma-Aldrich) onto freshly cleaved 1-in2 mica substrates. In our previous work, film thicknesses were found to range from 17.3 to 97.0 nm (based on atomic force microscope measurements) for polystyrene/toluene solutions ranging from 0.4 to 1.5 weight % polymer. Here, we used concentrations of 0.8 and 0.5% to yield films of 61.5 and 38.0 nm (which are referred to hereafter as 62 and 38 nm films). After the spin coating, the films were removed from the mica substrate by floating onto water and then collecting on a Teflon plate. Films were continually stacked until the weight was enough for a differential scanning calorimetry (DSC) sample. About 200 ultrathin films were stacked to obtain one 3–5 mg weight of DSC sample. Finally, the film was removed from the Teflon plate using a razor blade. To remove any residual solvent and/or adventitious water, the stacked ultrathin film samples were stored under the ambient conditions for 24 h and then annealed in vacuo at 50 °C and 5 Torr for 12 h prior to crimping the DSC pans. The same polystyrene sample in bulk was also studied.
DSC Measurements
The absolute heat capacity is measured by Perkin–Elmer Pyris 1 DSC with an ethylene glycol cooling system maintained at 5 °C in step scan mode, which consists of multiple temperature ramp/isothermal steps. The measurements are made on heating after first cooling the sample from 135 °C at 30 K/min; the methodology consists of 0.8 min isothermal holds every 2 K with 10 K/min ramps between temperatures. Calibration is performed using the same thermal history with sapphire, and this methodology was shown to give reliable measurements of absolute heat capacity in our previous study.23 Tg was obtained from the absolute Cp versus temperature data using the half-height method; that is, the temperature at which Cp attains a value halfway between the extrapolated liquid and glassy values is taken to be Tg. Sample sizes were 5.57 and 2.97 mg for the 62 and 38 nm ultrathin films, respectively. For the bulk, five different samples, reported in previous work,23 were used, ranging in size from 1.93 to 12.97 mg. The standard deviation of Tg for the bulk is ±0.2 K, independent of sample size.
In addition to using step scan, heating scan experiments were also performed in the Pyris1 DSC with ethylene glycol cooling system using the same stacked ultrathin film samples and different samples for the bulk. In one type of experiment, we measured the fictive temperature (Tf) on heating at a rate of 10 K/min after cooling at various rates, whereas in a second type of experiment, we measured the fictive temperature (Tf) as a function of aging time after isothermal structural relaxation. The fictive temperature is determined by Moynihan et al.'s method40 as the intersection of the extrapolated liquid and glass enthalpy lines. We note that when no isothermal aging occurs between the cooling and heating runs, as in the first type of experiment, the fictive temperature is termed the limiting fictive temperature (Tf′),43 and its value is approximately equal to Tg.47, 50 All measurements and aging experiments were made in a nitrogen atmosphere.
Prior to all experiments, samples were heated to 135 °C and held for 3 min in the DSC to erase their thermal history. For the cooling rate experiments, samples were then cooled to 35 °C at cooling rates ranging from 0.01 to 30 K/min, and then immediately heated again to 135 °C to obtain Tf (= Tf′). For the aging experiments, samples were cooled at 30 K/min from 135 °C to the aging temperature (Ta), aged isothermally for aging times ranging from 0 to 1000 min, and then cooled to 35 °C at 30 K/min; the fictive temperature was then measured on the subsequent heating scan at 10 K/min. The aging temperatures ranged from Tg − 15 K to Tg − 5 K, with Tg taken to be the value measured using step scan. Following each scan of the aged sample, the sample was cooled at 30 K/min from 135 °C and then heated at 10 K/min without aging; this provided an internal standard for the experiments to ensure that the sample did not change in the course of the experiments. Based on these “unaged” runs, the standard deviation in Tf′ is found to be ±0.5 K for the 62 nm film sample based on 29 “unaged” runs. A similar value is obtained for the bulk sample based on five heating runs for four different samples made after cooling at 30 K/min. Multiple runs were not made on the 38 nm sample.
The DSC temperature was calibrated with indium and a liquid crystal CE-3 ((+)-4-n-hexyloxyphenyl-4′-(2′-methylbutyl)-biphenyl-4-carboxylate) at 10 and 30 K/min; the isothermal temperature calibration, which is relevant for the step scan experiments and for setting the aging temperature Ta, was performed at 0.1 K/min, which was found in other work43 to be equivalent to performing an isothermal calibration. The absolute heat capacity was calibrated using sapphire.
Modeling Methodology
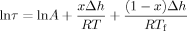 (2)
(2)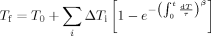 (3)
(3)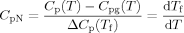 (4)
(4)DSC heating curves are each fit individually using the Marquardt algorithm.54 In addition, Tf versus aging time data is also fit simultaneously using this algorithm. The values of the parameters, β, x, and A, are obtained from the fits, whereas Δh/R is held constant at the value obtained from the cooling rate experimental data: 124,000 kK for the bulk and 99,500 kK for the 62 nm stacked ultrathin film sample, as shown later. The step size of temperature for the iteration is 0.1 K to minimize error during the fitting process.47
RESULTS
The absolute heat capacities of our stacked polystyrene samples composed of 62 nm and 38 nm films are compared with that of bulk polystyrene in Figure 1. The stacked ultrathin films show remarkable depressions of the absolute heat capacity from the bulk values in both liquid and glassy states. Interestingly, a greater depression is found in the liquid state than in the glass state; as a result, the step change in Cp at the glass transition, ΔCp is reduced. Similar behavior, in terms of the change Cp, was reported by us previously.23 Ellipsometry7, 21 and dielectric14 work on polystyrene ultrathin films shows similar results for the thermal expansion coefficient (α) at the nanoscale: a greater depression of α in the liquid state compared with that in the glass, and a corresponding reduction of the step change in α at the glass transition compared with the bulk. Temperature modulated DSC measurements of oligomeric propylene glycol and oligomeric methylphenylsiloxane also show decreases in ΔCp upon confinement in nanopores.26, 55, 56
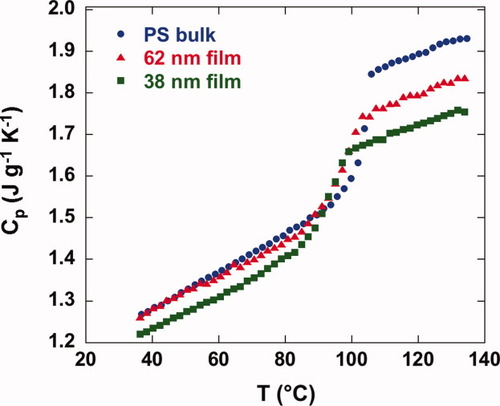
Absolute heat capacity versus temperature for bulk and stacked ultrathin film samples from step-scan DSC measured on heating after cooling at 30 K/min from 135 °C.
In addition to the changes in the absolute heat capacity and in ΔCp, the value of Tg, determined by the half-height method from the absolute heat capacity data, also decreases in the stacked ultrathin films. Tg is 103.8 °C for the bulk sample and decreases to 97.5 °C for the 62 nm and 92.7 °C for the 38 nm stacked ultrathin film giving 6.3 K and 11.1 K Tg reductions, respectively. The Tg values differ slightly from our previous work,23 being on average 2.8 ± 1.6 K higher in this work because in our previous work, Tg was inadvertently calculated as the half-width rather than the half-height value. Figure 2 shows the Tg depression for stacked polystyrene thin films as a function of film thickness for this work, along with recalculated results based on our previous work for films ranging from 17.3 to 97.0 nm spun-coated out of toluene solvents as well as toluene/acetone cosolvents and collected on teflon (as here) or with tweezers;23 the values of Tg, ΔCp, and ΔTg for all of the films studied are also tabulated in Table 1 with those from our previous work recalculated using the half-height method. The data are reasonably consistent with previously reported Tg depression values for supported polystyrene ultrathin films.
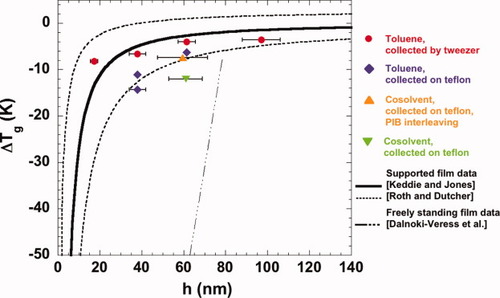
Tg of polystyrene ultrathin films as a function of film thickness from heating using step-scan after cooling from 135 °C at 10 K/min. Data from ref.23 are reanalyzed using the half-height method because the half-width method was inadvertently used in that work. Symbols are shown in the legend; the solvent indicates spin-coating solution solvent; see ref.23 for details of film preparation. The thick line is the best fit found in ref.4 for supported polystyrene thin films. The dotted thick lines are the best fits of lower and upper limits of the data reported in ref.5 for supported polystyrene thin films. The dash-dot line is from ref.6 for freely standing polystyrene thin films having a similar molecular weight to our sample.
| Film Preparation | Film Thickness (nm)b | ΔCp (J g−1 K−1) | Tgc (°C) | Tg − Tg bulk (°C) |
|---|---|---|---|---|
| None (bulk) | ∞ | 0.277 | 103.8 ± 0.2 | 0.0 |
| Spin coated from a toluene solution, floated onto water, and collected using tweezers | 97.0 ± 9.0 | 0.271 | 100.2 | −3.6 |
| 61.5 ± 4.1 | 0.258 | 99.8 | −4.0 | |
| 38.0 ± 4.0 | 0.246 | 97.2 | −6.6 | |
| 17.3 ± 1.7 | 0.223 | 95.6 | −8.2 | |
| Toluene solution; collected on Teflon | 61.5 | 0.211 | 97.5 | −6.3 |
| 38.0 | 0.202 | 92.7 | −11.1 | |
| 38.0 ± 4.0 | 0.218 | 89.5 | −14.3 | |
| Cosolvent solution; collected on Teflon; PIB interleaving | 59.5 ± 12.0 | 0.183 | 96.4 | −7.4 |
| Cosolvent solution; collected on Teflon | 61.0 ± 8.0 | 0.205 | 91.8 | −12.0 |
- a Values of ΔCp, Tg, and Tg − Tg,bulk include new data and data from ref.23 recalculated using the half-height method; data originally reported in ref.23 were inadvertently calculated using the half-width method.
- b When reported, the mean and standard deviation for film thickness are based on three measurements; when based on spin-coating concentration, only the nominal value is reported.
- c The standard deviation for the bulk Tg is based on measurements for five different samples.
As already mentioned in the introduction, the Tg depression depends on cooling rate. In this work, we examined the depression in the limiting fictive temperature, Tf′, which is obtained from a DSC heating scan immediately after cooling; the limiting fictive temperature depends only on cooling rate and approximates the glass transition temperature obtained on cooling at the same rate.47, 50 Figure 3 shows the DSC heating scans from which we will obtain Tf′, as a function of cooling rate from 0.01 K/min to 30 K/min for the bulk and stacked 62 nm ultrathin film samples. In these figures, we plot the normalized heat capacity, CpN, which is normalized for ease of comparison such that it is 0.0 in the glassy state and 1.0 in the liquid state. For both the bulk and ultrathin film samples, the magnitude of the enthalpy overshoot increases with decreasing cooling rate as expected. However, the stacked ultrathin film shows a dramatically reduced height of the enthalpy overshoot and a broader transition region than the bulk. The calculation results from TNM modeling are also shown in Figure 3 as dotted lines. The TNM model describes the bulk polystyrene DSC heating curves well, whereas the model shows more deviation from the data for the stacked ultrathin film sample. Nevertheless, the parameter β of the TNM model decreases in the stacked ultrathin films, consistent with a broadening of the relaxation time distribution in the ultrathin films. The TNM modeling results will be further summarized and discussed later.
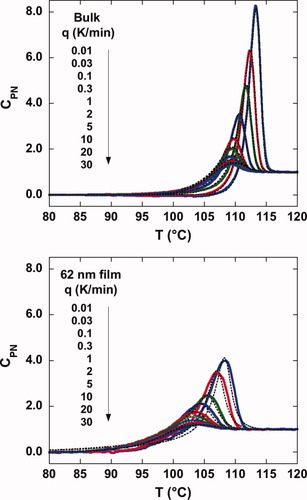
Normalized heat capacities as a function of cooling rate for the bulk (upper figure) and for stacked 62 nm ultrathin films (lower figure). The dotted lines are the results of TNM model fitting. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
The dependence of Tf′ on cooling rate is shown in Figure 4. As expected, Tf′ decreases with decreasing cooling rate. In addition, the dependence of Tf′ on cooling rate increases with decreasing film thickness in the stacked ultrathin film samples, yielding larger Tf′ depressions at lower cooling rates for the thinner films, in agreement with other researchers.7, 26 For the 38 nm film, Tg depressions are 13.8 K and 10.3 K at cooling rates of 0.01 K/min and 30 K/min, respectively. These results also support the supposition7 that the lack of a Tg reduction in nanocalorimetry18, 19 and AC calorimetric studies20 is attributable to the very fast cooling rates and high frequencies used in those methods. Also shown in Figure 4 as open symbols, the values of Tg obtained from the step scan method after cooling at 30 K/min are in reasonable agreement with those of Tf′ obtained from a normal scan on heating at 10 K/min also after cooling at the same rate. The values of Tf′ can be compared with the step-scan Tg also in Table 2. We note that standard deviations are only reported for Tf′ and Tg values in Table 2 when multiple measurements were made.
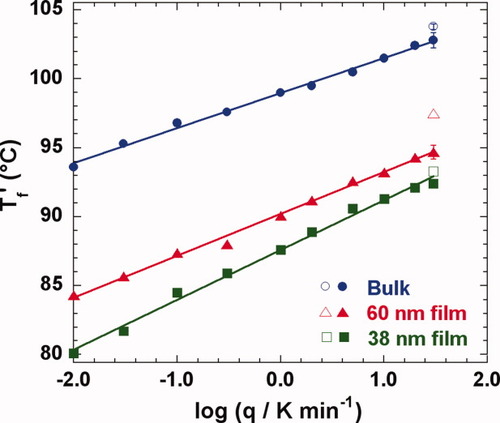
Cooling rate (q) dependence of the limiting fictive temperature (Tf′) for bulk and ultrathin film samples. Filled symbols represent Tf′ obtained from a normal DSC heating scan and open symbols represent Tg obtained from the step-scan method. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
| Sample | Tg (°C)a | Tf′ (°C)b | Δh/R (kK) | m |
|---|---|---|---|---|
| Bulk | 103.8 ± 0.2 | 102.8 ± 0.5 | 124 | 144 |
| 62 nm film | 97.5 | 94.6 ± 0.5 | 99 | 118 |
| 38 nm film | 92.7 | 92.4 | 81 | 98 |
- a Tg from step scan on heating after cooling at 30 K/min. The standard deviation is based on five different samples of previous work.23
- b Tf′ from a normal heating scan at 10 K/min after cooling at 30 K/min. The standard deviation is based multiple runs on one 62 nm film sample and for the bulk, on four different bulk samples.
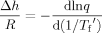 (5)
(5)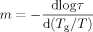 (6)
(6)As shown in Figure 3, slow cooling results in more relaxation during cooling and, hence, higher enthalpy overshoots and lower values of the limiting fictive temperature compared with a faster cooling rate. Similarly, isothermal structural relaxation or physical aging results in larger overshoots and lower fictive temperatures as aging time increases. Figure 5 shows the DSC heating scans as a function of aging time for the bulk and the 62 nm ultrathin film samples for an aging temperature (Ta) 5 K below the respective nominal Tg of each sample as measured with step scan. Again, we plot the normalized heat capacity, CpN, for ease of comparison. As aging time increases, the magnitude of the enthalpy overshoot increases, as expected. However, similar to the DSC scans after cooling at various rates, the stacked ultrathin film sample shows a reduced height of the enthalpy overshoot and a broader transition than the bulk for a given aging time; this is also similar to the DSC results observed for small molecules confined in nanopores after aging27 and similar to the early results of Kawana and Jones.21 The TNM model calculations are also shown as dotted lines in Figure 5. Similar to Figure 3, the fit is better for the bulk sample.
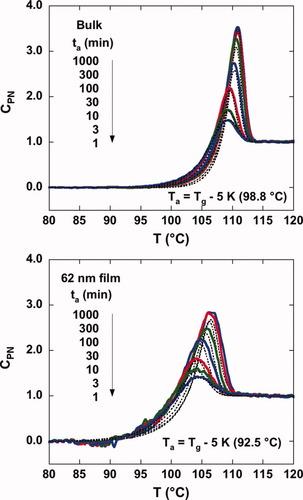
Normalized heat capacities as a function of the aging time at the aging temperature of Tg − 5 K for the bulk (upper figure) and for the stacked 62 nm ultrathin film sample (lower figure). The dotted lines are the results of TNM model fitting. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
The evolution of the fictive temperature (Tf) as a function of aging time can be calculated from the data shown in Figure 5, and this is shown in Figure 6 along with similar data for other aging temperatures. For ease of comparison, we plot the difference between the fictive temperature and the aging temperature (Tf − Ta) versus the logarithm of the aging time. The fictive temperature decreases nonexponentially as a function aging time, leveling off at equilibrium at a value where Tf = Ta; note that this differs from the case of aging in nanopore confinement27 where the 3-D constraints result in isotropic tensile stresses such that the equilibrium value of Tf does not equal Ta. The time required to reach equilibrium also increases as the aging temperature decreases. Comparing the physical aging behavior between the bulk and ultrathin film samples, the evolution of the fictive temperature and the rate of aging appears to be very similar for aging a given distance from each sample's Tg. However, since Tg is lower in the ultrathin film sample, at the same temperature, the stacked ultrathin film shows an acceleration of physical aging.
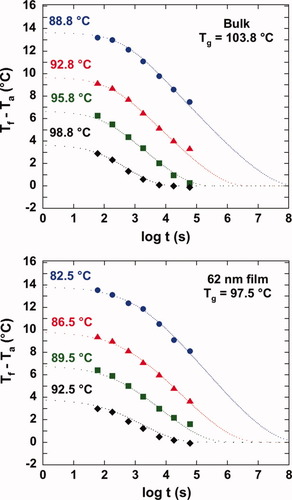
Evolution of fictive temperature during isothermal aging for the bulk (upper figure) and for the stacked 62 nm ultrathin film sample (lower figure) at the same distance from Tg: (•) Ta = Tg − 5 K, (▴) Ta = Tg − 8 K, (▪) Ta = Tg − 11 K, (♦) Ta = Tg − 15 K. The dotted lines are the results of TNM model fitting. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
The TNM model is able to describe the evolution of the fictive temperature with aging very well, and the fit is also shown in Figure 6. However, despite the similarity in the shape of the curves, large differences are found in TNM parameters for the bulk and stacked ultrathin film samples. The nonexponential parameter, β, is 0.807 for the bulk and 0.566 for the stacked ultrathin film sample, respectively, indicating that the stacked ultrathin film has a wider distribution of relaxation times.
DISCUSSION
The TNM model was fit to three types of data for both bulk and stacked ultrathin film samples: DSC heating scans after cooling at various rates, DSC heating scans after aging isothermally at various times, and fictive temperature versus aging time data at various isothermal temperatures. In all cases, the parameter β was smaller for the ultrathin films indicating a broadened relaxation time distribution. However, as shown in Table 3, the TNM model parameters obtained from fitting the three sets of data are quantitatively different, and for one data set, x decreases for the stacked ultrathin films, whereas for the other sets, it increases relative to the bulk value. In fact, the TNM model has documented shortcomings, including the inability to describe multiple data sets and to capture thermal history with one set of parameters, the lack of physical meaning of x, and a mutual dependence of β and x.24, 47, 48, 59-61 Nevertheless, the nonexponentiality parameter β for all three sets of data is lower for the stacked ultrathin films, which indicates that an increased distribution of relaxation times and a broadening of the glass transition is a distinct characteristic of nanoconfinement. Our stacked ultrathin film sample also shows a lower value of the fragility index (i.e., it is a stronger glass former as shown in Table 2) than the bulk despite its lower value of β (i.e., increased heterogeneity). Our observed positive correlation between fragility and nonexponentiality in confined geometry is inconsistent with the typical inverse correlation reported in the literature,62 but it is consistent with the results from other researchers studying supported polystyrene ultrathin films.13, 14
| Data Set | Bulk | 62 nm Film | ||
|---|---|---|---|---|
| β | x | β | x | |
| CpN vs. T as a f(q) | 0.482 ± 0.250 | 0.759 ± 0.121 | 0.285 ± 0.050 | 0.471 ± 0.355 |
| CpN vs. T as a f(ta) | ||||
| Ta = Tg − 5 K | 0.523 ± 0.104 | 0.675 ± 0.079 | 0.371 ± 0.022 | 0.553 ± 0.176 |
| Ta = Tg − 8 K | 0.443 ± 0.054 | 0.503 ± 0.158 | 0.340 ± 0.028 | 0.549 ± 0.280 |
| Ta = Tg − 11 K | 0.403 ± 0.072 | 0.456 ± 0.208 | 0.348 ± 0.060 | 0.599 ± 0.311 |
| Ta = Tg − 15 K | 0.364 ± 0.052 | 0.437 ± 0.240 | 0.337 ± 0.092 | 0.768 ± 0.315 |
| Tf vs. ta | 0.807 ± 0.05 | 0.308 ± 0.06 | 0.566 ± 0.05 | 0.415 ± 0.06 |
Compared with the bulk polystyrene sample, the sample of stacked 62 nm films shows a reduced height of the enthalpy overshoot and a broader transition for a given thermal history, as shown in both Figures 3 and 5. However, although the enthalpy overshoots have considerably different shapes, the evolution of Tf − Ta for the stacked ultrathin film seems to be the same as that of the bulk as shown Figure 6 for aging a given distance from Tg. To investigate the physical aging rate more quantitatively, the time required to reach equilibrium (t∞) is calculated as a function of the aging temperature and is plotted versus Tg − Ta in Figure 7 to account for the difference in Tg between the ultrathin film and bulk samples. Compared with the bulk, the stacked ultrathin film shows slightly longer times required to reach equilibrium when aged a comparable distance below Tg in the temperature range that we studied (near Tg). However, the slope of the t∞ versus Tg − Ta is 17% lower for the stacked ultrathin film sample such that below approximately Ta = Tg − 15 K, the films are expected to come to equilibrium faster than the bulk when aged at the same distance from Tg. This difference in slopes is quantitatively consistent with the higher cooling rate dependence (weaker temperature dependence) shown in Figure 4. The inset in Figure 7 shows the comparison between the time required to reach equilibrium as a function of aging temperature; at any given aging temperature, the ultrathin film sample reaches equilibrium faster than the bulk sample.
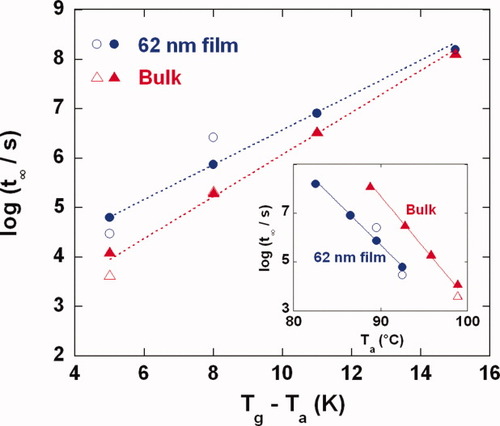
The time to reach equilibrium versus the size of the temperature down jump for bulk and 62 nm ultrathin film samples. Filled symbols represent the values obtained from TNM model, and open symbols represent the values obtained from KWW fitting near equilibrium. The inset shows the time to reach equilibrium versus the aging temperature. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
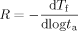 (7)
(7)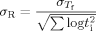 (8)
(8)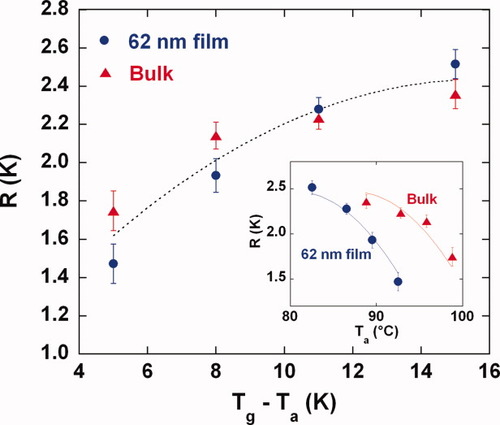
The aging rate (R = −dTf/dlog ta) versus the size of the temperature down jump for bulk and 62 nm ultrathin film samples. The aging rates were calculated from the slope of Tf versus log ta in the linear region. The inset shows the aging rates versus the aging temperature. Lines are guides for the eye only. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
The inset in Figure 8 shows the aging rate R as a function of aging temperature. In this comparison, the ultrathin film sample shows a lower aging rate than the bulk at a given aging temperature for the aging temperatures studied presumably because of the depressed Tg of the ultrathin film and the smaller driving force to reach equilibrium. Priestley et al.29 found a similar result when aging below the bulk Tg but above Tg of an ultrathin polystyrene film supported on quartz although in that case the ultrathin film did not age at all because it was in equilibrium. When aging the same samples 71 K below the bulk Tg (i.e., at 29 °C) for aging times to 4800 s, Priestley et al.29 reported that the aging rate was considerably lower for the ultrathin film sample; however, it is not clear that the linear decay region (where, for example, volume decreases linearly with the logarithm of time) can be accurately determined in 4800 s for aging so far below Tg—see for example, Figure 6 where we would be hard pressed to obtain a rate from the linear decay region for aging 15 K below Tg if we had data only to 4800 s. Greiner and Schwarzl63 have argued that reaching the linear decay region is necessary for calculating a meaningful aging rate. On the other hand, Huang and Paul30, 31 found that the aging rate at temperatures more than 130 K below Tg increased for thin (micron-size) films and that the aging rate decreased with decreasing temperature. Although these findings seem to be inconsistent with our results, we suggest that the difference may be due to the different temperature ranges of the studies. Greiner and Schwarzl63 showed that for a sufficiently wide range of aging temperature, the aging rate increases with decreasing aging temperature near Tg, reaches a maximum aging rate, and then decreases as the aging temperature decreases further. We are in the regime close to Tg where the aging rate is increasing with decreasing temperature, whereas Huang and Paul's study was done in the regime far from Tg.
More importantly, however, we argue that the aging rate near Tg is not necessarily indicative of whether aging is accelerated or not because in this regime, the aging rate depends both on the distance from Tg (the driving force) and the temperature. In other words, a low aging rate can indicate either that the material is very close to equilibrium (such that the aging rate does not reflect the relaxation time) or that the relaxation time is long. We showed that the times required to reach equilibrium are significantly lower for the ultrathin film samples compared with the bulk at a given aging temperature - indicating that aging is accelerated. Hence, the fact that the aging rate is lower for the thin films at a given aging temperature simply indicates that the samples are closer to equilibrium, and it does not indicate that the relaxation times are longer.
CONCLUSIONS
The effects of ultrathin film confinement on the glass transition of polystyrene and its kinetics, including structural recovery, were investigated by DSC using stacked ultrathin film samples. Measurements were made of the fictive temperature as a function of cooling rate and as a function of aging time at various isothermal aging temperatures. The reduced height of the enthalpy overshoot and the broadened transition in DSC heating scan curves are found to be characteristics of ultrathin film confinement and seem to result from a broadened distribution of relaxation times, as supported by a decrease of the TNM model parameter β for the ultrathin film sample. The limiting fictive temperature of the ultrathin film sample increases more than that of the bulk sample with increasing cooling rate, such that the magnitude of Tg depression decreases with increasing cooling rate, and the apparent activation energy and fragility decrease for the thin films. At high enough cooling rates, no Tg depression may exist in agreement with other researchers in the field. In addition, the enthalpy relaxation of the ultrathin film sample shows similar behavior to the bulk for aging at the same distance below Tg, as shown in terms of the time to reach equilibrium and the physical aging rate. However, at a given aging temperature, acceleration of physical aging in terms of the time required to reach equilibrium is observed in the ultrathin film sample presumably because it is closer to Tg due to the Tg depression in the ultrathin film sample. For aging in the regime near Tg, the aging rate is not a good indicator of whether or not aging is accelerated.
Acknowledgements
The authors gratefully acknowledge funding from NSF DMR 0304640.




