A fast maximum flow algorithm
Funding information: Office of Naval Research, N00014-17-1-2194
Abstract
In 2013, Orlin proved that the max flow problem could be solved in O(nm) time. His algorithm ran in O(nm + m1.94) time, which was the fastest for graphs with fewer than n1.06 arcs. If the graph was not sufficiently sparse, the fastest running time was an algorithm due to King, Rao, and Tarjan. We describe a new variant of the excess scaling algorithm for the max flow problem whose running time strictly dominates the running time of the algorithm by King et al. For graphs in which m = O(nlog n), the running time of our algorithm dominates that of King et al. by a factor of O(loglog n). Moreover, our algorithm achieves this improved performance without reliance on dynamic trees.



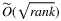 iterations and faster algorithms for maximum flow
iterations and faster algorithms for maximum flow
