RESEARCH ARTICLE
Linear stability for a free boundary tumor model with a periodic supply of external nutrients
Yaodan Huang,
Zhengce Zhang,
Bei Hu,
Yaodan Huang
School of Mathematics and Statistics, Xi'an Jiaotong University, Xi'an, PR China
Search for more papers by this authorCorresponding Author
Zhengce Zhang
School of Mathematics and Statistics, Xi'an Jiaotong University, Xi'an, PR China
Correspondence
Zhengce Zhang, School of Mathematics and Statistics, Xi'an Jiaotong University, Xi'an 710049, PR China.
Email: [email protected]
Communicated by: S. Wise
Search for more papers by this authorBei Hu
Department of Applied Computational Mathematics and Statistics, University of Notre Dame, Notre Dame, Indiana
Search for more papers by this authorYaodan Huang,
Zhengce Zhang,
Bei Hu,
Yaodan Huang
School of Mathematics and Statistics, Xi'an Jiaotong University, Xi'an, PR China
Search for more papers by this authorCorresponding Author
Zhengce Zhang
School of Mathematics and Statistics, Xi'an Jiaotong University, Xi'an, PR China
Correspondence
Zhengce Zhang, School of Mathematics and Statistics, Xi'an Jiaotong University, Xi'an 710049, PR China.
Email: [email protected]
Communicated by: S. Wise
Search for more papers by this authorBei Hu
Department of Applied Computational Mathematics and Statistics, University of Notre Dame, Notre Dame, Indiana
Search for more papers by this authorAbstract
In this paper, we consider a free boundary tumor model with a periodic supply of external nutrients, so that the nutrient concentration σ satisfies σ = ϕ(t) on the boundary, where ϕ(t) is a positive periodic function with period T. A parameter μ in the model is proportional to the “aggressiveness” of the tumor. If
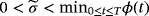, where
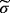is a threshold concentration for proliferation, Bai and Xu [Pac J Appl Math. 2013;5;217-223] proved that there exists a unique radially symmetric T-periodic positive solution (σ∗(r,t),p∗(r,t),R∗(t)), which is stable for any μ > 0 with respect to all radially symmetric perturbations.17 We prove that under nonradially symmetric perturbations, there exists a number μ∗ such that if 0 < μ < μ∗, then the T-periodic solution is linearly stable, whereas if μ > μ∗, then the T-periodic solution is linearly unstable.
REFERENCES
- 1Adam J. A simplified mathematical model of tumor growth. Math Biosci. 1986; 81: 229-244. https://doi.org/10.1016/0025-5564(86)90119-7
- 2Adam J. Mathematical model of tumor growth. III. Comparison with experiment. Math Biosci. 1987; 86: 213-227. https://doi.org/10.1016/0025-5564(87)90011-3
- 3Adam J, Bellomo N. A Survey of Models for Tumor-Immune System Dynamics. Boston: Birkhäuser; 1997.
10.1007/978-0-8176-8119-7 Google Scholar
- 4Anderson A. A hybrid mathematical model of solid tumour invasion: the importance of cell adhesion. Math Med Biol. 2005; 22: 163-186. https://doi.org/10.1093/imammb/dqi005
- 5Anderson A, Chaplain M. Continuous and discrete mathematical models of tumor-induced angiogenesis. Bull Math Biol. 1998; 60: 857-900. https://doi.org/10.1006/bulm.1998.0042
- 6Byrne H. The importance of intercellular adhesion in the development of carcinomas. IMA J Math Appl Med Biol. 1997; 14: 305-323. https://doi.org/10.1093/imammb/14.4.305
- 7Byrne H, Chaplain M. Growth of nonnecrotic tumors in the presence and absence of inhibitors. Math Biosci. 1995; 130: 151-181. https://doi.org/10.1016/0025-5564(94)00117-3
- 8Byrne H, Chaplain M. Growth of necrotic tumors in the presence and absence of inhibitors. Math Biosci. 1996; 135: 187-216. https://doi.org/10.1016/0025-5564(96)00023-5
- 9Byrne H, Chaplain M. Modelling the role of cell-cell adhesion in the growth and development of carcinomas. Math Comput Modell. 1996; 24: 1-17. https://doi.org/10.1016/S0895-7177(96)00174-4
- 10Byrne H, Chaplain M. Free boundary value problems associated with the growth and development of multicellular spheroids. European J Appl Math. 1997; 8: 639-658.
- 11Greenspan H. Models for the growth of a solid tumor by diffusion. Stud Appl Math. 1972; 51: 317-340. https://doi.org/10.1002/sapm1972514317
- 12Greenspan H. On the growth and stability of cell cultures and solid tumors. J Theoret Biol. 1976; 56: 229-242. https://doi.org/10.1016/S0022-5193(76)80054-9
- 13Levine H, Pamuk S, Sleeman B. Mathematical modeling of capillary formation and development in tumor angiogenesis: penetration into the stroma. Bull Math Biol. 2001; 63: 801-863. https://doi.org/10.1006/bulm.2001.0240
- 14Pettet G, Please C, Tindall M, McElwain D. The migration of cells in multicell tumor spheroids. Bull Math Biol. 2001; 63: 231-257. https://doi.org/10.1006/bulm.2000.0217
- 15Ward J, King J. Mathematical modelling of avascular-tumour growth. IMA J Math Appl Med Biol. 1997; 14: 39-69. https://doi.org/10.1093/imammb/14.1.39
- 16Ward J, King J. Mathematical modelling of avascular-tumour growth II: modelling growth saturation. IMA J Math Appl Med Biol. 1999; 16: 171-211. https://doi.org/10.1093/imammb/16.2.171
- 17Bai M, Xu S. Qualitative analysis of a mathematical model for tumor growth with a periodic supply of external nutrients. Pac J Appl Math. 2013; 5: 217-223.
- 18Bazaliy B, Friedman A. Global existence and asymptotic stability for an elliptic-parabolic free boundary problem: an application to a model of tumor growth. Indiana Univ Math J. 2003; 52: 1265-1304.
- 19Chen X, Cui S, Friedman A. A hyperbolic free boundary problem modeling tumor growth: asymptotic behavior. Tran Amer Math Soc. 2005; 357: 4771-4804. https://doi.org/10.1090/S0002-9947-05-03784-0
- 20Cui S. Analysis of a mathematical model for the growth of tumors under the action of external inhibitors. J Math Biol. 2002; 44: 395-426. https://doi.org/10.1007/s002850100130
- 21Cui S. Asymptotic stability of the stationary solution for a hyperbolic free boundary problem modeling tumor growth. SIAM J Math Anal. 2008; 40: 1692-1724. https://doi.org/10.1137/080717778
- 22Cui S. Lie group action and stability analysis of stationary solutions for a free boundary problem modelling tumor growth. J Differ Equ. 2009; 246: 1845-1882.
- 23Cui S. Asymptotic stability of the stationary solution for a parabolic-hyperbolic free boundary problem modeling tumor growth. SIAM J Math Anal. 2013; 45: 2870-2893. https://doi.org/10.1137/130906271
- 24Cui S. Linearized stability for a multi-dimensional free boundary problem modelling two-phase tumor growth. Nonlinearity. 2014; 27: 1045-1079.
- 25Cui S, Escher J. Asymptotic behaviour of solutions of a multidimensional moving boundary problem modeling tumor growth. Comm Partial Differ Equ. 2008; 33: 636-655. https://doi.org/10.1080/03605300701743848
- 26Cui S, Escher J. Well-posedness and stability of a multi-dimensional tumor growth model. Arch Ration Mech Anal. 2009; 191: 173-193. https://doi.org/10.1007/s00205-008-0158-9
- 27Cui S, Friedman A. Analysis of a mathematical model of the effect of inhibitors on the growth of tumors. Math Biosci. 2000; 164: 103-137. https://doi.org/10.1016/S0025-5564(99)00063-2
- 28Cui S, Friedman A. Analysis of a mathematical model of the growth of necrotic tumors. J Math Anal Appl. 2001; 255: 636-677. https://doi.org/10.1006/jmaa.2000.7306
- 29Escher J, Matioc A-V. Radially symmetric growth of nonnecrotic tumors. Nonlinear Differ Equ Appl. 2010; 17: 1-20. https://doi.org/10.1007/s00030-009-0037-6
- 30Escher J, Matioc A-V. Well-posedness and stability analysis for a moving boundary problem modelling the growth of nonnecrotic tumors. Discrete Contin Dyn Syst Ser B. 2011; 15: 573-596. https://doi.org/10.3934/dcdsb.2011.15.573
- 31Escher J, Matioc A-V. Analysis of a two-phase model describing the growth of solid tumors. European J Appl Math. 2013; 24: 25-48. https://doi.org/10.1017/S0956792512000290
- 32Friedman A, Hu B. Bifurcation from stability to instability for a free boundary problem arising in a tumor model. Arch Ration Mech Anal. 2006; 180: 293-330. https://doi.org/10.1007/s00205-005-0408-z
- 33Friedman A, Hu B. Asymptotic stability for a free boundary problem arising in a tumor model. J Differ Equ. 2006; 227: 598-639. https://doi.org/10.1016/j.jde.2005.09.008
- 34Friedman A, Hu B. Stability and instability of Liapunov-Schmidt and Holf bifurcation for a free boundary problem arising in a tumor model. Trans Amer Math Soc. 2008; 360: 5291-5342. https://doi.org/10.1090/S0002-9947-08-04468-1
- 35Friedman A, Lam K-Y. Analysis of a free-boundary tumor model with angiogenesis. J Differ Equ. 2015; 259: 7636-7661. https://doi.org/10.1016/j.jde.2015.08.032
- 36Friedman A, Reitich F. Analysis of a mathematical model for the growth of tumors. J Math Biol. 1999; 38: 262-284. https://doi.org/10.1007/s002850050149
- 37Friedman A, Reitich F. Symmetry-breaking bifurcation of analytic solutions to free boundary problems: an application to a model of tumor growth. Trans Amer Math Soc. 2001; 353: 1587-1634. https://doi.org/10.1090/S0002-9947-00-02715-X
- 38Hao W, Hauenstein J, Hu B, Sommese A. A three-dimensional steady-state tumor system. Appl Math Comput. 2011; 218: 2661-2669. https://doi.org/10.1016/j.amc.2011.08.006
- 39Hao W, Hauenstein J, Hu B, Liu Y, Sommese A, Zhang Y. Continuation along bifurcation branches for a tumor model with a necrotic core. J Sci Comput. 2012; 53: 395-413. https://doi.org/10.1007/s10915-012-9575-x
- 40Hao W, Hauenstein J, Hu B, McCoy T, Sommese A. Computing steady-state solutions for a free boundary problem modeling tumor growth by Stokes equation. J Comput Appl Math. 2013; 237: 326-334. https://doi.org/10.1016/j.cam.2012.06.001
- 41Huang Y, Zhang Z, Hu B. Bifurcation for a free-boundary tumor model with angiogenesis. Nonlinear Anal Real World Appl. 2017; 35: 483-502. https://doi.org/10.1016/j.nonrwa.2016.12.003
- 42Wu J. Analysis of a mathematical model for tumor growth with Gibbs-Thomson relation. J Math Anal Appl. 2017; 450: 532-543. https://doi.org/10.1016/j.jmaa.2017.01.051
- 43Wu J, Cui S. Asymptotic behaviour of solutions of a free boundary problem modelling the growth of tumours in the presence of inhibitors. Nonlinearity. 2007; 20: 2389-2408.
- 44Wu J, Cui S. Asymptotic behavior of solutions for parabolic differential equations with invariance and applications to a free boundary problem modeling tumor growth. Discrete Contin Dyn Syst. 2010; 26: 737-765. https://doi.org/10.3934/dcds.2010.26.737
- 45Wu J, Zhou F. Asymptotic behavior of solutions of a free boundary problem modeling tumor spheroid with Gibbs-Thomson relation. J Differ Equ. 2017; 262: 4907-4930. https://doi.org/10.1016/j.jde.2017.01.012
- 46Xu S, Chen Y, Bai M. Analysis of a free boundary problem for avascular tumor growth with a periodic supply of nutrients. Discrete Contin Dyn Syst Ser B. 2016; 21: 997-1008. https://doi.org/10.3934/dcdsb.2016.21.997
- 47Xu S, Bai M, Zhang F. Analysis of a time-delayed mathematical model for tumour growth with an almost periodic supply of external nutrients. J Biol Dyn. 2017; 11: 504-520.
- 48Zhou F, Cui S. Well-posedness and stability of a multidimensional moving boundary problem modeling the growth of tumor cord. Discrete Contin Dyn Syst. 2008; 21: 929-943. https://doi.org/10.3934/dcds.2008.21.929
- 49Zhou F, Escher J, Cui S. Well-posedness and stability of a free boundary problem modeling the growth of multi-layer tumors. J Differ Equ. 2008; 244: 2909-2933. https://doi.org/10.1016/j.jde.2008.02.038
- 50Zhou F, Wu J. Stability and bifurcation analysis of a free boundary problem modelling multi-layer tumours with Gibbs-Thomson relation. European J Appl Math. 2015; 26: 401-425. https://doi.org/10.1017/S0956792515000108
- 51Zhou F, Wu J, Cui S. Existence and asymptotic behavior of solutions to a moving boundary problem modeling the growth of multi-layer tumors. Comm Pure Appl Anal. 2009; 8: 1669-1688. https://doi.org/10.3934/cpaa.2009.8.1669
- 52Lowengrub J, Frieboes H, Jin F, et al. Nonlinear modelling of cancer: bridging the gap between cells and tumours. Nonlinearity. 2010; 23: 1-91.
- 53Erdelyi A, Magnus W, Oberhettinger F, Tricomi F. Higher Transcendental Functions, Vol. II. New York: McGraw-Hill; 1953.
- 54Friedman A, Reitich F. Nonlinear stability of a quasi-static Stefan problem with surface tension: a continuation approach. Ann Sc Norm Super Pisa CI Sci. 2001; 30: 341-403.
