Mathematical Methods in the Applied Sciences

Volume 42, Issue 3 pp. 871-882

RESEARCH ARTICLE

Upper semicontinuity of global attractors for a viscoelastic equations with nonlinear density and memory effects

Yony Raúl Santaria Leuyacc,

Corresponding Author

Yony Raúl Santaria Leuyacc

[email protected]

orcid.org/0000-0001-8279-7460

Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo, São Carlos-SP, Brazil

Facultad de Ciencias Matemáticas, Universidad Nacional Mayor de San Marcos, Lima, Perú

Correspondence

Yony Raúl Santaria Leuyacc, Matemáticas e de Computação, Universidade de São Paulo, São Carlos-SP 13560-970, Brazil.

Email: [email protected]

Communicated by: K. Yildirim

Search for more papers by this author

Jorge Luis Crisostomo Parejas,

Jorge Luis Crisostomo Parejas

orcid.org/0000-0002-9049-4125

Dirección de estudios generales, Universidad San Ignacio de Loyola, Lima, Peru

Facultad de Ciencias Matemáticas, Universidad Nacional Mayor de San Marcos, Lima, Perú

Search for more papers by this author

Yony Raúl Santaria Leuyacc,

Corresponding Author

Yony Raúl Santaria Leuyacc

[email protected]

orcid.org/0000-0001-8279-7460

Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo, São Carlos-SP, Brazil

Facultad de Ciencias Matemáticas, Universidad Nacional Mayor de San Marcos, Lima, Perú

Correspondence

Yony Raúl Santaria Leuyacc, Matemáticas e de Computação, Universidade de São Paulo, São Carlos-SP 13560-970, Brazil.

Email: [email protected]

Communicated by: K. Yildirim

Search for more papers by this author

Jorge Luis Crisostomo Parejas,

Jorge Luis Crisostomo Parejas

orcid.org/0000-0002-9049-4125

Dirección de estudios generales, Universidad San Ignacio de Loyola, Lima, Peru

Facultad de Ciencias Matemáticas, Universidad Nacional Mayor de San Marcos, Lima, Perú

Search for more papers by this author

First published: 04 December 2018

https://doi.org/10.1002/mma.5389

Citations: 4

Share a link

Email
Wechat
Bluesky

Abstract

This paper is devoted to showing the upper semicontinuity of global attractors associated with the family of nonlinear viscoelastic equations

$urn:x-wiley:mma:media:mma5389:mma5389-math-0001$

in a three-dimensional space, for f growing up to the critical exponent and dependent on ρ ∈ [0,4), as ρ→0⁺. This equation models extensional vibrations of thin rods with nonlinear material density ϱ(∂_tu) = |∂_tu|^ρ and presence of memory effects. This type of problems has been extensively studied by several authors; the existence of a global attractor with optimal regularity for each ρ ∈ [0,4) were established only recently. The proof involves the optimal regularity of the attractors combined with Hausdorff's measure.

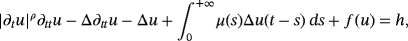
REFERENCES

1Love AH. A Treatise on Mathematical Theory of Elasticity. New York: Dover; 1944.
Google Scholar
2Bogolubsky IL. Some examples of inelastic soliton interaction. Comput Phys Comm. 1977; 13: 149-155.
10.1016/0010-4655(77)90009-1
Web of Science® Google Scholar
3Cavalcanti MM, Domingos Cavalcanti VN, Ferreira J. Existence and uniform decay for a non-linear viscoelastic equation with strong damping. Math Methods Appl Sci. 2001; 24: 1043-1053.
10.1002/mma.250
Web of Science® Google Scholar
4Conti M, Ma TF, Marchini EM, Seminario Huertas PN. Asymptotics of viscoelastic materials with nonlinear density and memory effects. J Differ Equ. 2018; 264: 4235-4259.
10.1016/j.jde.2017.12.010
Web of Science® Google Scholar
5Cavalcanti MM, Portillo Oquendo H. Frictional versus viscoelastic damping in a semilinear wave equation. SIAM J Control Optim. 2003; 42: 1310-1324.
10.1137/S0363012902408010
Web of Science® Google Scholar
6Di Plinio F, Pata V, Zelik S. On the strongly damped wave equation with memory. Indiana Univ Math J. 2008; 57: 757-780.
10.1512/iumj.2008.57.3266
Web of Science® Google Scholar
7Giorgi C, Muñoz Rivera JE, Pata V. Global attractors for a semilinear hyperbolic equation in viscoelasticity. J Math Anal Appl. 2001; 260: 83-99.
10.1006/jmaa.2001.7437
Web of Science® Google Scholar
8Messaoudi SA. General decay of solutions of a viscoelastic equation. J Math Anal Appl. 2008; 341: 1457-1467.
10.1016/j.jmaa.2007.11.048
Web of Science® Google Scholar
9Cavalcanti MM, Domingos Cavalcanti VN, Lasiecka I, Webler CM. Intrinsic decay rates for the energy of a nonlinear viscoelastic equation modeling theb vibrations of thin rods with variable density. Adv Nonlinear Anal. 2016; 6: 121-145.
Web of Science® Google Scholar
10Han X, Wang M. General decay of energy for a viscoelastic equation with nonlinear damping. Math Methods Appl Sci. 2009; 32: 346-358.
10.1002/mma.1041
Web of Science® Google Scholar
11Han X, Wang M. Global existence and uniform decay for a nonlinear viscoelastic equation with damping. Nonlinear Anal. 2009; 70: 3090-3098.
10.1016/j.na.2008.04.011
Web of Science® Google Scholar
12Liu W. Uniform decay of solutions for a quasilinear system of viscoelastic equations. Nonlinear Anal. 2009; 71: 2257-2267.
10.1016/j.na.2009.01.060
Web of Science® Google Scholar
13Liu W. General decay and blow-up of solution for a quasilinear viscoelastic problem with nonlinear source. Nonlinear Anal. 2010; 73: 1890-1904.
10.1016/j.na.2010.05.023
Web of Science® Google Scholar
14Messaoudi SA, Mustafa MI. A general stability result for a quasilinear wave equation with memory. Nonlinear Anal Real World Appl. 2013; 14: 1854-1864.
10.1016/j.nonrwa.2012.12.002
Web of Science® Google Scholar
15Messaoudi SA, Tatar NE. Global existence and uniform stability of solutions for a quasilinear viscoelastic problem. Math Methods Appl Sci. 2007; 30: 665-680.
10.1002/mma.804
Web of Science® Google Scholar
16Messaoudi SA, Tatar NE. Exponential decay for a quasilinear viscoelastic equation. Math Nachr. 2009; 282: 1443-1450.
10.1002/mana.200610800
Web of Science® Google Scholar
17Park JY, Park SH. General decay for quasilinear viscoelastic equations with nonlinear weak damping. J Math Phys. 2009; 50(8): 10.
10.1063/1.3187780
Web of Science® Google Scholar
18Wu ST. Arbitrary decays for a viscoelastic equation. Bound Value Probl. 2011; 2011: 1-14.
10.1186/1687-2770-2011-28
Web of Science® Google Scholar
19Messaoudi SA, Tatar NE. Exponential and polynomial decay for a quasilinear viscoelastic equation. Nonlinear Anal. 2008; 68: 785-793.
10.1016/j.na.2006.11.036
Web of Science® Google Scholar
20Araujo RO, Ma TF, Qin Y. Long-time behavior of a quasilinear viscoelastic equation with past history. J Differ Equ. 2013; 254: 4066-4087.
10.1016/j.jde.2013.02.010
Web of Science® Google Scholar
21Conti M, Marchini EM, Pata V. A well posedness result for nonlinear viscoelastic equations with memory. Nonlinear Anal. 2014; 94: 206-216.
10.1016/j.na.2013.08.015
Web of Science® Google Scholar
22Conti M, Marchini EM, Pata V. Global attractors for nonlinear viscoelastic equations with memory. Commun Pure Appl Anal. 2016; 15: 1893-1913.
10.3934/cpaa.2016021
Web of Science® Google Scholar
23Qin Y, Zhang J, Sun L. Upper semicontinuity of pullback attractors for a non-autonomous viscoelastic equation. Appl Math Comput. 2013; 223: 362-376.
10.1016/j.amc.2013.08.034
Web of Science® Google Scholar
24Qin Y, Feng B, Zhang M. Uniform attractors for a non-autonomous viscoelastic equation with a past history. Nonlinear Anal. 2014; 101: 1-15.
10.1016/j.na.2014.01.006
Web of Science® Google Scholar
25Grasselli M, Pata V. Upper semicontinuous attractor for a hyperbolic phase-field model with memory. Indiana Univ Math J. 2001; 50: 1281-1308.
10.1512/iumj.2001.50.2122
Web of Science® Google Scholar
26Hale JK, Raugel G. Upper semicontinuity of the attractor for a singularly perturbed hyperbolic equation. J Differ Equ. 1988; 73: 197-214.
10.1016/0022-0396(88)90104-0
Web of Science® Google Scholar
27Pata V, Zucchi A. Attractors for a damped hyperbolic equation with linear memory. Adv Math Sci Appl. 2001; 11: 505-529.
Google Scholar
28Dafermos CM. Asymptotic stability in viscoelasticity. Arch Ration Mech Anal. 1970; 37: 297-308.
10.1007/BF00251609
Web of Science® Google Scholar
29Chueshov I, Lasiecka I. Long-time behavior of second order evolution equations with nonlinear damping. Mem Amer Math Soc. 2008; 195(912): 1-183.
Web of Science® Google Scholar
30Temam R. Infinite-Dimensional Dynamical Systems in Mechanics and Physics. New York: Springer; 1988.
10.1007/978-1-4684-0313-8
Web of Science® Google Scholar
31Babin AV, Vishik MI. Attractors of Evolution Equations. North-Holland, Amsterdam: Elsevier Science Pub; 1992.
Google Scholar
32Hale JK. Asymptotic Behavior of Dissipative Systems. Providence, R.I.: American Mathematical Society; 1988.
Google Scholar
33Miranville A, Zelik S. Attractors for Dissipative Partial Differential Equations in Bounded and Unbounded Domains. In: CM Dafermos, M Pokorny, eds. Handbook of Differential Equations, Evolutionary Equations, Chapter 3, vol. 4. Amsterdam: Elsevier; 2008: 103-200.
10.1016/S1874-5717(08)00003-0
Google Scholar
34Seminario Huertas PN. Atratores globais para uma equação viscoelástica não linear com história. Dissertação (Mestrado em Matemática). São Carlos: Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo; 2015.
Google Scholar
35Haraux A. Systèmes Dynamiques Dissipatifs Et Applications. Paris: Masson; 1991.
Google Scholar

Citing Literature

Volume42, Issue3

February 2019

Pages 871-882

Upper semicontinuity of global attractors for a viscoelastic equations with nonlinear density and memory effects

Abstract

REFERENCES

Citing Literature

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Upper semicontinuity of global attractors for a viscoelastic equations with nonlinear density and memory effects

Abstract

REFERENCES

Citing Literature

References

Related

Information