Stability, periodicity, and symmetries of certain second-order fractional difference equation with quadratic terms via KAM theory
Mirela Garić-Demirović
Department of Mathematics, University of Tuzla, Tuzla, 75000 Bosnia and Herzegovina
Search for more papers by this authorCorresponding Author
M. Nurkanović
Department of Mathematics, University of Tuzla, Tuzla, 75000 Bosnia and Herzegovina
Correspondence to: M. Nurkanović, Department of Mathematics, University of Tuzla, 75000 Tuzla, Bosnia and Herzegovina
E-mail: [email protected]
Search for more papers by this authorZ. Nurkanović
Department of Mathematics, University of Tuzla, Tuzla, 75000 Bosnia and Herzegovina
Search for more papers by this authorMirela Garić-Demirović
Department of Mathematics, University of Tuzla, Tuzla, 75000 Bosnia and Herzegovina
Search for more papers by this authorCorresponding Author
M. Nurkanović
Department of Mathematics, University of Tuzla, Tuzla, 75000 Bosnia and Herzegovina
Correspondence to: M. Nurkanović, Department of Mathematics, University of Tuzla, 75000 Tuzla, Bosnia and Herzegovina
E-mail: [email protected]
Search for more papers by this authorZ. Nurkanović
Department of Mathematics, University of Tuzla, Tuzla, 75000 Bosnia and Herzegovina
Search for more papers by this authorAbstract
By using the Kolmogorov–Arnold–Moser theory, we investigate the stability of the equilibrium solution of the difference equation
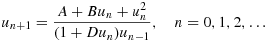
References
- 1Kulenović MRS, Merino O. Discrete Dynamical Systems and Difference Equations with Mathematica. Chapman and Hall/CRC: Boca Raton, London, 2002.
10.1201/9781420035353 Google Scholar
- 2Bastien G, Rogalski M. On the algebraic difference equations un + 2un=ψ(un + 1) in
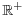, related to a family of elliptic quartics in the plane. Advances in Difference Equations 2005; 2005(3): 227–261.
- 3Bastien G, Rogalski M. On the algebraic difference equations un + 2+un=ψ(un + 1) in
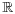, related to a family of elliptic quartics in the plane. Journal of Mathematical Analysis and Applications 2007; 326(2): 822–844.
- 4Cima A, Gasull A, Mańosa V. Dynamics of rational discrete dynamical systems via first integrals. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering 2006; 16: 631–645.
- 5Janowski EJ, Kulenović MRS, Nurkanović Z. Stability of the k-th order Lyness’ equation with a period-k coefficient. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering 2007; 17: 143–152.
- 6Kocic VL, Ladas G, Tzanetopoulos G, Thomas E. On the stability of Lyness' equation. Dynamics of Continuous, Discrete and Impulsive Systems 1995; 1: 245–254.
- 7Kulenović MRS, Nurkanović Z. Stability of Lyness' equation with period-three coefficient. Radovi Matematicki 2004; 12: 153–161.
- 8Kulenović MRS, Nurkanović Z. Stability of Lyness'n equation with period-two coefficient via KAM theory. Journal of Concrete and Applicable Mathematics 2008; 6: 229–245.
- 9Ladas G, Tzanetopoulos G, Tovbis A. On May's host parasitoid model. Journal of Difference Equations and Applications 1996; 2: 195–204.
10.1080/10236199608808054 Google Scholar
- 10Gidea M, Meiss JD, Ugarcovici I, Weiss H. Applications of KAM theory to population dynamics. Journal of Biological Dynamics 2011; 5(1): 44–63.
- 11Kulenović MRS, Nurkanović Z, Pilav E. Birkhoff normal forms and KAM theory for Gumowski-Mira equation. The Scientific World Journal 2014; 2014: Article ID 819290, 8 p.
- 12Papaschinopoulos G, Schinas CJ. Stability of a class of nonlinear difference equations. Journal of Mathematical Analysis and Applications 1999; 230: 211–222.
- 13Beukers F, Cushman R. Zeeman's monotonicity conjecture. Journal of Differential Equations 1998; 143: 191–200.
- 14Zeeman EC. Geometric Unfolding of a Difference Equation, Preprint. Hertford College: Oxford, 1996.
- 15Cima A, Gasull A, Mańosa V. Non-autonomous two-periodic Gumowski-Mira difference equation. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering 2012; 16: 14p.
- 16Clark CA, Janowski EJ, Kulenović MRS. Stability of the Gumowski-Mira equation with period-two coefficient. Journal of Mathematical Analysis and Applications 2005; 307: 292–304.
- 17Kulenović MRS. Invariants and related Liapunov functions for difference equations. Applied Mathematics Letters 2000; 13: 1–8.
- 18Gumowski I, Mira C. Recurrences and Discrete Dynamic Systems, Lecture Notes in Mathematics. Springer: Berlin, 1980.
10.1007/BFb0089135 Google Scholar
- 19del-Castillo-Negrete D, Greene JM, Morrison EJ. Area preserving nontwist maps: periodic orbits and transition to chaos. Physica D 1996; 91: 1–23.
