Research Article
Existence of renormalized solutions to a nonlinear parabolic equation in L1 setting with nonstandard growth condition and gradient term
Zhongqing Li,
Wenjie Gao,
Corresponding Author
Zhongqing Li
College of Mathematics, Jilin University, Changchun 130012, China
Correspondence to: Zhongqing Li, College of Mathematics, Jilin University, Changchun 130012, China.
E-mail: [email protected]
Search for more papers by this authorWenjie Gao
College of Mathematics, Jilin University, Changchun 130012, China
Search for more papers by this authorZhongqing Li,
Wenjie Gao,
Corresponding Author
Zhongqing Li
College of Mathematics, Jilin University, Changchun 130012, China
Correspondence to: Zhongqing Li, College of Mathematics, Jilin University, Changchun 130012, China.
E-mail: [email protected]
Search for more papers by this authorWenjie Gao
College of Mathematics, Jilin University, Changchun 130012, China
Search for more papers by this authorAbstract
This paper is devoted to the study of a nonlinear parabolic p(x)-Laplace equation with gradient term and L1 data. The authors obtain the existence of renormalized solutions via strong convergence of truncation. Copyright © 2014 John Wiley & Sons, Ltd.
References
- 1Zhikov VV. On Lavrentiev's phenomenon. Russian Journal of Mathematical Physics 1995; 3(2): 249–269.
- 2Zhikov VV. Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 2004; 310. Kraev. Zadachi Mat. Fiz. i Smezh. Vopr. Teor. Funkts. 35 [34]: 67–81, 226.
- 3Samko S. Denseness of
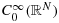in the generalized Sobolev spaces
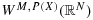. In Direct and Inverse Problems of Mathematical Physics (Newark, DE, 1997). vol. 5 of Int. Soc. Anal. Appl. Comput. Kluwer Academic Publishers: Dordrecht, 2000; 333–342.
10.1007/978-1-4757-3214-6_20 Google Scholar - 4Diening L, Harjulehto P, Hästö P, Ru̇żiċka M. Lebesgue and Sobolev Spaces with Variable Exponents. vol. 2017 of Lecture Notes in Mathematics. Springer: Heidelberg, 2011.
- 5Ru̇żiċka M. Electrorheological Fluids: Modeling and Mathematical Theory. vol. 1748 of Lecture Notes in Mathematics. Springer-Verlag: Berlin, 2000.
- 6Antontsev SN, Rodrigues JF. On stationary thermo-rheological viscous flows. Annali dell'Università di Ferrara. Sezione VII. Scienze Matematiche 2006; 52(1): 19–36.
10.1007/s11565-006-0002-9 Google Scholar
- 7Chiadò Piat V, Coscia A. Hölder continuity of minimizers of functionals with variable growth exponent. Manuscripta Mathematica 1997; 93(3): 283–299.
- 8Zhikov VV. Averaging of functionals of the calculus of variations and elasticity theory. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya 1986; 50(4): 675–710, 877.
- 9Chen Y, Levine S, Rao M. Variable exponent, linear growth functionals in image restoration. SIAM Journal on Applied Mathematics 2006; 66(4): 1383–1406 (electronic).
- 10DiPerna RJ, Lions PL. On the Cauchy problem for Boltzmann equations: global existence and weak stability. Annals of Mathematics 1989; 130(2): 321–366.
- 11Boccardo A, Diaz JI, Giachetti D, Murat F. Existence of a solution for a weaker form of a nonlinear elliptic equation. In Recent Advances in Nonlinear Elliptic and Parabolic Problems (Nancy, 1988). vol. 208 of Pitman Res. Notes Math. Ser. Longman Sci. Tech.: Harlow, 1989; 229–246.
- 12Porretta A. Existence results for nonlinear parabolic equations via strong convergence of truncations. Annali di Matematica Pura ed Applicata 1999; 177(4): 143–172.
- 13Carrillo J, Wittbold P. Renormalized entropy solutions of scalar conservation laws with boundary condition. Journal of Differential Equations 2002; 185(1): 137–160.
- 14Blanchard D, Murat F. Renormalised solutions of nonlinear parabolic problems with L1 data: existence and uniqueness. Proceedings of the Royal Society of Edinburgh Section A 1997; 127(6): 1137–1152.
- 15Blanchard D, Murat F, Redwane H. Existence and uniqueness of a renormalized solution for a fairly general class of nonlinear parabolic problems. Journal of Differential Equations 2001; 177(2): 331–374.
- 16Dall'Aglio A, Orsina L. Nonlinear parabolic equations with natural growth conditions and L1 data. Nonlinear Analysis 1996; 27(1): 59–73.
- 17Xu X. On the initial-boundary value problem for ut−div(|∇u|p − 2∇u) = 0. Archive for Rational Mechanics and Analysis 1994; 127(4): 319–335.
- 18Zhang C, Zhou S. Renormalized and entropy solutions for nonlinear parabolic equations with variable exponents and L1 data. Journal of Differential Equations 2010; 248(6): 1376–1400.
- 19Bendahmane M, Wittbold P, Zimmermann A. Renormalized solutions for a nonlinear parabolic equation with variable exponents and L1-data. Journal of Differential Equations 2010; 249(6): 1483–1515.
- 20Landes R. On the existence of weak solutions for quasilinear parabolic initial-boundary value problems. Proceedings of the Royal Society of Edinburgh: Section A 1981; 89(3-4): 217–237.
10.1017/S0308210500020242 Google Scholar
- 21Boccardo L, Murat F, Puel JP. Existence results for some quasilinear parabolic equations. Nonlinear Analysis 1989; 13(4): 373–392.
- 22Fan X, Zhao D. On the spaces Lp(x)(Ω) and Wm,p(x)(Ω). Journal of Mathematical Analysis and Applications 2001; 263(2): 424–446.
- 23Kováčik O, Rákosník J. On spaces Lp(x) and Wk,p(x). Czechoslovak Mathematical Journal 1991; 41((116)(4)): 592–618.
- 24Edmunds DE, Rákosník J. Sobolev embeddings with variable exponent. Studia Mathematica 2000; 143(3): 267–293.
- 25Blanchard D. Truncations and monotonicity methods for parabolic equations. Nonlinear Analysis 1993; 21(10): 725–743.
- 26Bénilan P, Boccardo L, Gallouët T, Gariepy R, Pierre M, Vázquez JL. An L1-theory of existence and uniqueness of solutions of nonlinear elliptic equations. Annali della Scuola Normale Superiore di Pisa - Classe di Scienze (4) 1995; 22(2): 241–273.
- 27Mokrane A. Existence of bounded solutions of some nonlinear parabolic equations. Proceedings of the Royal Society of Edinburgh Section A 1987; 107(3-4): 313–326.
10.1017/S0308210500031188 Google Scholar
- 28Boccardo L, Gallouët T, Orsina L. Existence and nonexistence of solutions for some nonlinear elliptic equations. SIAM Journal on Mathematical Analysis 1997; 73: 203–223.
- 29DiBenedetto E. Real analysis. Birkhäuser Advanced Texts: Basler Lehrbücher. [Birkhäuser Advanced Texts: Basel Textbooks]. Birkhäuser Boston Inc.: Boston, MA, 2002.
10.1007/978-1-4612-0117-5 Google Scholar
- 30Lions JL. Quelques méthodes de résolution des problèmes aux limites non linéaires. Dunod: Paris, 1969.
- 31Zeidler E. Nonlinear Functional Analysis and its Applications. II/B. Springer-Verlag: New York, 1990. Nonlinear monotone operators. Translated from the German by the author and Leo F. Boron.
- 32Simon J. Compact sets in the space Lp(0,T;B). Annali di Matematica Pura ed Applicata 1987; 146(4): 65–96.
