Large-time behavior of a two-scale semilinear reaction–diffusion system for concrete sulfatation
Toyohiko Aiki
Department of Mathematical and Physical Sciences, Faculty of Science, Japan Women's University, 2-8-1 Mejirodai, Bunkyo-ku, Tokyo 112-8681, Japan
Search for more papers by this authorCorresponding Author
Adrian Muntean
Centre for Analysis, Scientific computing and Applications (CASA), Institute for Complex Molecular Systems (ICMS), Department of Mathematics and Computer Science, Eindhoven University of Technology, The Netherlands
Correspondence to: Adrian Muntean, Centre for Analysis, Scientific computing and Applications (CASA), Institute for Complex Molecular Systems (ICMS), Department of Mathematics and Computer Science, Eindhoven University of Technology, The Netherlands.
E-mail: [email protected]
Search for more papers by this authorToyohiko Aiki
Department of Mathematical and Physical Sciences, Faculty of Science, Japan Women's University, 2-8-1 Mejirodai, Bunkyo-ku, Tokyo 112-8681, Japan
Search for more papers by this authorCorresponding Author
Adrian Muntean
Centre for Analysis, Scientific computing and Applications (CASA), Institute for Complex Molecular Systems (ICMS), Department of Mathematics and Computer Science, Eindhoven University of Technology, The Netherlands
Correspondence to: Adrian Muntean, Centre for Analysis, Scientific computing and Applications (CASA), Institute for Complex Molecular Systems (ICMS), Department of Mathematics and Computer Science, Eindhoven University of Technology, The Netherlands.
E-mail: [email protected]
Search for more papers by this authorAbstract
We study the large-time behavior of (weak) solutions to a two-scale reaction–diffusion system coupled with a nonlinear ordinary differential equations modeling the partly dissipative corrosion of concrete (or cement)-based materials with sulfates. We prove that as t → ∞ , the solution to the original two-scale system converges to the corresponding two-scale stationary system. To obtain the main result, we make use essentially of the theory of evolution equations governed by subdifferential operators of time-dependent convex functions developed combined with a series of two-scale energy-like time-independent estimates. Copyright © 2014 John Wiley & Sons, Ltd.
References
- 1 Fatima T, Muntean A. Sulfate attack in sewer pipes: derivation of a concrete corrosion model via two-scale convergence. Nonlinear Analysis: Real World Applications 2014; 15(1): 326–344.
- 2 Allaire G. Homogenization and two-scale convergence. SIAM Journal on Mathematical Analysis 1992; 23(6): 1482–1518.
- 3 Nguestseng G. A general convergence result for a functional related to the theory of homogenization. SIAM Journal on Mathematical Analysis 1989; 20: 608–623.
- 4 Hornung U, Jäger W. Diffusion, convection, adsorption, and reaction of chemicals in porous media. Journal of Differential Equations 1991; 92(2): 199–225.
- 5 Aregba-Driollet D, Diele F, Natalini R. A mathematical model for the sulphur dioxide aggression to calcium carbonate stones: numerical approximation and asymptotic analysis. SIAM Journal on Applied Mathematics 2004; 64(5): 1636–1667.
- 6 Böhm M, Rosen IG. Global weak solutions and uniqueness for a moving boundary problem for a coupled system of quasilinear diffusion-reaction equations arising as a model of chemical corrosion of concrete surfaces – (part 3), Preprints aus dem Institut für Mathematik, Institut für Mathematik, 1996.
- 7 Gleize PJP, Motta EV, Silva DA, Roman HR. Characterization of historical mortars from Santa Catarina (Brazil). Cement and Concrete Composites 2009; 31(5): 342–346.
- 8 Fatima T, Muntean A, Aiki T. Distributed space scales in a semilinear reaction-diffusion system including a parabolic variational inequality: a well-posedness study. Advanced Mathematical Sciences and Applications 2012; 22: 295–318.
- 9 Battino R, Clever HL. The solubility of gases in liquids. Chemical Reviews 1966; 66(4): 395–463.
- 10
Barenblatt GI,
Zheltov IP,
Kochina IN. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks. Journal of Applied Mathematics and Mechanics 1960; 24(5): 1286–1303.
10.1016/0021-8928(60)90107-6 Google Scholar
- 11 Böhm M, Showalter RE. Diffusion in fissured media. SIAM Journal on Mathematical Analysis 1985; 16(3): 500–509.
- 12 Cook JD, Showalter RE. Microstructure diffusion models with secondary flux. Journal of Mathematical Analysis and Applications 1995; 189(3): 731–756.
- 13 Hornung U, Showalter RE. Diffusion models for fractured media. Journal of Mathematical Analysis and Applications 1990; 147(1): 69–80.
- 14 Showalter RE, Walkington J. Micro-structure models of diffusion in fissured media. Journal of Mathematical Analysis and Applications 1991; 155: 1–20.
- 15 Meier SA, Böhm M. A note on the construction of function spaces for distributed-microstructure models with spatially varying cell geometry. International Journal of Numerical Analysis and Modeling 2008; 5(5): 109–125.
- 16 Meier SA. Two-scale models for reactive transport and evolving microstructure, Ph.D. Thesis, University of Bremen, Germany, 2008.
- 17 Meier SA, Muntean A. A two-scale reaction-diffusion system with micro-cell reaction concentrated on a free boundary. Comptes Rendus Mécanique 2008; 336(6): 481–486.
- 18 Meier SA, Muntean A. A two-scale reaction-diffusion system: homogenization and fast-reaction limits. GAKUTO International Series Mathematical Sciences and Applications 2010; 32: 441–459.
- 19 Escher J, Treutler D. Strong solutions of semilinear matched microstruture models. Journal of Evolution Equations 2012; 12(2): 459–480.
- 20 Treutler D. Well-posedness for a quasilinear generalization of the matched microstructure model. Nonlinear Analysis: Real World Applications 2012; 13(6): 2622–2632.
- 21 Arbogast T, Douglas J, Hornung U. Derivation of the double porosity model of single phase flow via homogenization theory. SIAM Journal on Mathematical Analysis 1990; 21: 813–826.
- 22
Bourgeat A,
Chechkin G,
Piatnitski A. Singular double porosity model. Applicable Analysis 2003; 82: 103–116.
10.1080/0003681031000063739 Google Scholar
- 23 Jäger W, Neuss-Radu M. Effective transmission conditions for reaction-diffusion process in domains separated by an interface. SIAM Journal on Mathematical Analysis 2007; 39: 687–720.
- 24
Panfilov M. Macroscale Models of Flow through Highly Heterogeneous Porous Media. Kluwer: Dordrecht, 2000.
10.1007/978-94-015-9582-7 Google Scholar
- 25 U Hornung (ed). Homogenization and Porous Media, Interdisciplinary Applied Mathematics, vol. 6, Springer-Verlag: New York, 1997.
10.1007/978-1-4612-1920-0 Google Scholar
- 26 Friedman A, Knabner P. A transport model with micro- and macro-structure. Journal of Differential Equations 1992; 98(2): 328–354.
- 27 Friedman A, Tzavaras AE. A quasilinear parabolic system arising in modelling of catalytic reactors. Journal of Differential Equations 1987; 70(2): 167–196.
- 28 Antonic N. Memory effects in homogenisation: linear second-order equations. Archive for Rational Mechanics and Analysis 1993; 125(1): 1–24.
- 29 Muntean A, Neuss-Radu M. A multiscale Galerkin approach for a class of nonlinear coupled reaction-diffusion systems in complex media. Journal of Mathematical Analysis and Applications 2010; 371(2): 705–718.
- 30 Aiki T, Muntean A. Large time behavior of solutions to a moving-interface problem modeling concrete carbonation. Communications on Pure and Applied Analysis 2010; 9(5): 1117–1129.
- 31
Aiki T,
Muntean A. A free-boundary problem for concrete carbonation: rigorous justification of the
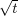-law of propagation. Interfaces and Free Boundaries 2013; 15(2): 167–180.
- 32 Zemskov SV, Ahmad B, Copuroglu O, Vermolen FJ. Modeling of a self-healing process in blast furnace slag cement exposed to accelerated carbonation. Journal of Physics: Conference Series 2013; 410(1). 012088.
- 33 Yamada Y. On evolution equations generated by subdifferential operators. Journal of the Faculty of Science University of Tokyo Section IA-Mathematics 1976; 23(3): 491–515.
- 34 Kenmochi N. Solvability of nonlinear evolution equations with time-dependent constraints and applications. Bulletin on Faculty Education, Chiba University 1981; 30: 1–87.
- 35
Ladyzenskaja OA,
Solonnikov VA,
Uralce'va NN. Linear and Quasi-linear Equations of Parabolic Type, Translations of Mathematical Monographs, vol. 23, AMS: Providence, Rhode Island, USA, 1968.
10.1090/mmono/023 Google Scholar
