Homogeneous polynomials and extensions of Hardy-Hilbert's inequality
Corresponding Author
Vasileios A. Anagnostopoulos
School of Electrical and Computer Engineering, National Technical University, Zografou Campus 15780, Athens, Greece
Vasileios A. Anagnostopoulos, School of Electrical and Computer Engineering, National Technical University, Zografou Campus 15780, Athens, Greece, Phone: +30 210 867 9077, Fax: +30 210 7721775
Yannis Sarantopoulos, Department of Mathematics, National Technical University, Zografou Campus 15780, Athens, Greece, Phone: +30 210 772 1765, Fax: +30 210 772 1775
Andrew M. Tonge, Department of Mathematical Sciences, Kent State University, Kent OH 44242, USA, Phone: +1 330 672 9046, Fax: +1 330 672 2209
Search for more papers by this authorCorresponding Author
Yannis Sarantopoulos
Department of Mathematics, National Technical University, Zografou Campus 15780, Athens, Greece
Vasileios A. Anagnostopoulos, School of Electrical and Computer Engineering, National Technical University, Zografou Campus 15780, Athens, Greece, Phone: +30 210 867 9077, Fax: +30 210 7721775
Yannis Sarantopoulos, Department of Mathematics, National Technical University, Zografou Campus 15780, Athens, Greece, Phone: +30 210 772 1765, Fax: +30 210 772 1775
Andrew M. Tonge, Department of Mathematical Sciences, Kent State University, Kent OH 44242, USA, Phone: +1 330 672 9046, Fax: +1 330 672 2209
Search for more papers by this authorCorresponding Author
Andrew M. Tonge
Department of Mathematical Sciences, Kent State University, Kent OH 44242, USA
Vasileios A. Anagnostopoulos, School of Electrical and Computer Engineering, National Technical University, Zografou Campus 15780, Athens, Greece, Phone: +30 210 867 9077, Fax: +30 210 7721775
Yannis Sarantopoulos, Department of Mathematics, National Technical University, Zografou Campus 15780, Athens, Greece, Phone: +30 210 772 1765, Fax: +30 210 772 1775
Andrew M. Tonge, Department of Mathematical Sciences, Kent State University, Kent OH 44242, USA, Phone: +1 330 672 9046, Fax: +1 330 672 2209
Search for more papers by this authorCorresponding Author
Vasileios A. Anagnostopoulos
School of Electrical and Computer Engineering, National Technical University, Zografou Campus 15780, Athens, Greece
Vasileios A. Anagnostopoulos, School of Electrical and Computer Engineering, National Technical University, Zografou Campus 15780, Athens, Greece, Phone: +30 210 867 9077, Fax: +30 210 7721775
Yannis Sarantopoulos, Department of Mathematics, National Technical University, Zografou Campus 15780, Athens, Greece, Phone: +30 210 772 1765, Fax: +30 210 772 1775
Andrew M. Tonge, Department of Mathematical Sciences, Kent State University, Kent OH 44242, USA, Phone: +1 330 672 9046, Fax: +1 330 672 2209
Search for more papers by this authorCorresponding Author
Yannis Sarantopoulos
Department of Mathematics, National Technical University, Zografou Campus 15780, Athens, Greece
Vasileios A. Anagnostopoulos, School of Electrical and Computer Engineering, National Technical University, Zografou Campus 15780, Athens, Greece, Phone: +30 210 867 9077, Fax: +30 210 7721775
Yannis Sarantopoulos, Department of Mathematics, National Technical University, Zografou Campus 15780, Athens, Greece, Phone: +30 210 772 1765, Fax: +30 210 772 1775
Andrew M. Tonge, Department of Mathematical Sciences, Kent State University, Kent OH 44242, USA, Phone: +1 330 672 9046, Fax: +1 330 672 2209
Search for more papers by this authorCorresponding Author
Andrew M. Tonge
Department of Mathematical Sciences, Kent State University, Kent OH 44242, USA
Vasileios A. Anagnostopoulos, School of Electrical and Computer Engineering, National Technical University, Zografou Campus 15780, Athens, Greece, Phone: +30 210 867 9077, Fax: +30 210 7721775
Yannis Sarantopoulos, Department of Mathematics, National Technical University, Zografou Campus 15780, Athens, Greece, Phone: +30 210 772 1765, Fax: +30 210 772 1775
Andrew M. Tonge, Department of Mathematical Sciences, Kent State University, Kent OH 44242, USA, Phone: +1 330 672 9046, Fax: +1 330 672 2209
Search for more papers by this authorAbstract
If L is a continuous symmetric n-linear form on a real or complex Hilbert space and \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$\widehat{L}$\end{document}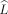
is the associated continuous n-homogeneous polynomial, then \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$\Vert L\Vert =\big \Vert \widehat{L}\big \Vert$\end{document}
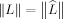. We give a simple proof of this well-known result, which works for both real and complex Hilbert spaces, by using a classical inequality due to S. Bernstein for trigonometric polynomials. As an application, an open problem for the optimal lower bound of the norm of a homogeneous polynomial, which is a product of linear forms, is related to the so-called permanent function of an n × n positive definite Hermitian matrix. We have also derived generalizations of Hardy-Hilbert's inequality.
References
- 1 N. I. Achieser, Theory of Approximation (Dover Publ., 1992).
- 2 B. Anderson, J. M. Ash, R. L. Jones, D. G. Rider, and B. Saffari, Exponential sums with coefficients 0 or 1 and concentrated Lp norms, Ann. Inst. Fourier 57(5), 1377–1404 (2007).
- 3 J. Arias-de Reyna, Gaussian variables, polynomials and permanents, Linear Algebra Appl. 285, 107–114 (1998).
- 4 K. M. Ball, The complex plank problem, Bull. Lond. Math. Soc. 33, 433–442 (2001).
- 5
S. Banach,
Über homogene Polynome in (L2),
Stud. Math. 7, 36–44 (1938).
10.4064/sm-7-1-36-44 Google Scholar
- 6 C. Benítez and Y. Sarantopoulos, Characterization of real inner product spaces by means of symmetric bilinear forms, J. Math. Anal. Appl. 180, 207–220 (1993).
- 7 C. Benítez, Y. Sarantopoulos, and A. M. Tonge, Lower bounds for norms of products of polynomials, Math. Proc. Camb. Philos. Soc. 124, 395–408 (1998).
- 8 S. N. Bernstein, Sur une propriété des fonctions entières, C. R. Acad. Sci. 176, 1603–1605 (1923).
- 9 R. P. Boas, Entire Functions (Academic Press, 1954).
- 10 J. Bochnak and J. Siciak, Polynomials and multilinear mappings in topological vector spaces, Stud. Math. 39, 59–76 (1971).
- 11 J. G. van der Corput and G. Schaake, Ungleichungen für Polynome und trigonometrische Polynome, Compos. Math. 2, 321–361 (1935); Berichtigung, Compos. Math. 3, 128 (1936).
- 12
S. Dineen,
Complex Analysis on Infinite Dimensional Spaces (Springer-Verlag, London, 1999).
10.1007/978-1-4471-0869-6 Google Scholar
- 13 P. L. Duren, Theory of Hp Spaces (Dover Publ., 2000).
- 14
R. E. Edwards,
Fourier Series Vol. 2, second ed. (Springer–Verlag, 1982).
10.1007/978-1-4613-8156-3 Google Scholar
- 15
D. Foschi,
Some remarks on the \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$L^p\mbox{-}L^q$\end{document}
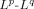boundedness of trigonometric sums and oscillatory integrals,
Commun. Pure Appl. Anal. 4(3), 569–588 (2005).
- 16 J. C. García-Vázquez and R. Villa, Lower bounds for multilinear forms defined on Hilbert spaces, Matematika 46, 315–322 (1999).
- 17 G. H. Hardy, J. E. Littlewood, and G. Pólya, Inequalities, second ed. (Cambridge University Press, 1988).
- 18 L. A. Harris, Bounds on the derivatives of holomorphic functions of vectors, in: Analyse fonctionnelle et applications (Comptes Rendus Colloq. Analyse, Inst. Mat., Univ. Federal Rio de Janeiro, Rio de Janeiro, 1972), 145–163, Actualités Aci. Indust., No. 1367 (Hermann, Paris, 1975).
- 19 H. Helson, Harmonic Analysis (Addison–Wesley, 1983).
- 20
L. Hörmander,
On a theorem of Grace,
Math. Scand. 2, 55–64 (1954).
10.7146/math.scand.a-10395 Google Scholar
- 21
O. D. Kellogg,
On bounded polynomials in several variables,
Math. Z. 27, 55–64 (1928).
10.1007/BF01171085 Google Scholar
- 22 E. H. Lieb, Proofs on some conjectures on permanents, J. Math. Mech. 16, 127–134 (1966).
- 23 A. E. Litvak, V. D. Milman, and G. Schechtman, Averages of norms and quasi-norms, Math. Ann. 312, 95–124 (1998).
- 24
M. Marcus and
H. Minc,
The Pythagorean theorem in certain symmetry classes of tensors,
Trans. Am. Math. Soc. 104, 510–515 (1962).
10.1090/S0002-9947-1962-0139626-2 Google Scholar
- 25 M. Marcus, The permanent analogue of the Hadamard determinant theorem, Bull. Am. Math. Soc. 69, 494–496 (1963).
- 26
M. Marcus,
A lower bound for the product of linear forms,
Linear Multilinear Algebra 43, 115–120 (1997).
10.1080/03081089708818519 Google Scholar
- 27 I. Masri and A. Tonge, Norm estimates for random multilinear Hankel forms, Linear Algebra Appl. 402, 255–262 (2005).
- 28 A. Pappas and Sz. Révész, Linear polarization constants of Hilbert spaces, J. Math. Anal. Appl. 300, 129–146 (2004).
- 29 A. Pappas, Y. Sarantopoulos, and A. Tonge, Norm attaining polynomials, Bull. Lond. Math. Soc. 39, 255–264 (2007).
- 30 T. H. Pate, The best lower bound for the permanent of a correlation matrix of rank two, Linear Multilinear Algebra 51, 263–278 (2003).
- 31 Sz. Révész and Y. Sarantopoulos, Plank problems, polarization and Chebyshev constants, J. Korean Math. Soc. 41(1), 157–174 (2004).
- 32 Y. Sarantopoulos, Estimates for polynomial norms on Lp(μ) spaces, Math. Proc. Camb. Philos. Soc. 99, 263–271 (1986).
- 33 R. Salem and A. Zygmund, Some properties of trigonometric series whose terms have random signs, Acta Math. 91, 245–301 (1954).
- 34 A. M. Tonge, The failure of Bernstein's theorem for polynomials on C(K) spaces, J. Approx. Theory 51, 160–162 (1987).
- 35
Xie, Hong-zheng and
Lü, Zhong-xue,
Discrete Hardy-Hilbert's inequalities in \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$\mathbf {R}^{n}$\end{document}
,
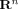Northeast. Math. J. 21(1), 87–94 (2005).
- 36
A. Zygmund,
Trigonometric Series, third ed. (Cambridge University Press, 2003).
10.1017/CBO9781316036587 Google Scholar
