Humeral short stem varus–valgus alignment affects bone stress
Abstract
The use of uncemented humeral stems in total shoulder arthroplasty (TSA) is associated with stress shielding. Shorter length stems have shown to decrease stress shielding; however, the effect of stem varus–valgus alignment is currently not known. The purpose of this study was to quantify the effect of short stem distal humeral endosteal contact due to varus–valgus angulation on bone stresses after TSA. Three-dimensional models of eight male cadaveric humeri were constructed from computed tomography data. Bone models were reconstructed with a short stem humeral component implant in three positions (standard, varus, and valgus). Modeling was performed at 45° and 75° of abduction and the resulting differentials in bone stress compared to the intact state and the expected time-zero bone response were determined. In cortical and trabecular bone, the standard position (STD) altered bone stress less than the valgus (VAL) and varus (VAR) positions relative to the intact state. For both cortical (p = 0.033) and trabecular (p = 0.012) bone, the VAL position produced a larger volume of bone with resorbing potential compared to the STD position.
1 INTRODUCTION
Total shoulder arthroplasty (TSA) is an effective treatment to restore shoulder function and alleviate pain in patients with glenohumeral arthritis. On the humeral side, the articular surface of the humeral head is removed, and the proximal humerus is reamed to allow the humeral stem to be inserted into the canal. Stress shielding induced bone resorption following TSA is thought to be due to the replacement of bone with a stiffer metallic implant, resulting in reduced bone loading.1-3 Raiss et al.4 found stress-shielding occurred in 63% of a cohort of 103 patients who received a TSA with an uncemented standard length humeral stem with a mean follow-up time of 5 years. To help reduce the risk of stress shielding, alterations to humeral stem design include reduced stem length, changes to the implant surface characteristics in regions of bony contact, and modifications to proximal stem geometry.
Recent reports of clinical outcomes of short stem humeral stem components have been favorable and stress shielding was less frequently observed with some implants when compared to standard length stems. In a study by Casagrande et al.,5 11% of all patients who received a short stem press-fit humeral implant (73 TSAs) had humeral loosening, and close to 9% of all patients in the 24 months follow-up group (69 TSAs) were considered at risk of loosening with stress shielding mentioned as a probable cause. According to Schnetzke et al.,6 a series of patients that underwent TSA had good clinical outcomes when a short stem prosthesis was used, and no evidence of loosening was observed.
Clinical studies have also investigated differences in various short stem humeral designs. Radiographic changes of patients following TSA with two different short stem humeral implants were reported by Denard et al.7 who found varying mean total radiographic change scores for the two designs. They hypothesized that this was due to differences in the overall shape and surface treatments of the two stem designs. In another study by Morwood et al.8 patients treated with coated ministem humeral components were less likely to have radiographic features of loosening when compared to patients treated with uncoated stems.
Peduzzi et al.9 reported good midterm results for short uncemented implants with no stem-related complications, although proximal bony adaptations were observed in more than 80% of the cases. Additionally, both Peduzzi et al.9 and Langohr et al.10 reported that smaller-sized humeral short stem implants may reduce the risk for bony adaptations and result in humeral bone stresses that more closely approximate the intact state when compared to larger-sized implants. It was also suggested that stem axis deviation can increase the risk of stress shielding9.
While clinical data seems to suggest that error in the placement of humeral short stems could have negative consequences in terms of humeral stress shielding, the actual effects of varus–valgus malpositioning on bone stress and expected bone response immediately following surgery are not well understood. The purpose of this study was to quantify the effect of distal humeral short stem endosteal contact due to varus–valgus malpositioning on humeral cortical and trabecular bone stresses after TSA. We hypothesized that central positioning of the humeral stem within the canal avoiding distal cortical contact would produce less stress shielding compared to stems having either varus or valgus distal humeral cortical contact.
2 METHODS
2.1 Finite element simulation and model development
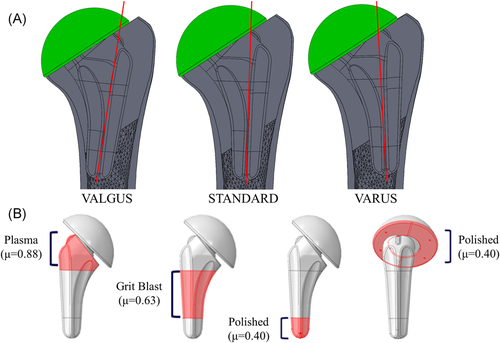
The three-dimensional geometries of eight male cadaveric humeri (average age: 68 ± 6 years, 8 L) were obtained using computed tomography (CT) data that was obtained in conjunction with a density phantom (qCT Pro model 3; Mindways Software) in the field of view to permit the calibration of CT attenuation. All specimens were prescreened for evidence of significant degeneration and/or humeral deformities. The CT data were imported into MIMICS (Materialize) for model generation and material designation. To separate the cortical and trabecular sections of the humerus, the incorporation of both automatic threshold-based and manual segmentation methods was used. These humeral bone models were then virtually reconstructed three times by an orthopedic surgeon (K. J. F.) using a short stem humeral implant (Exactech Equinoxe® Preserve) that was placed directly in the center of the humeral canal (STD), in valgus alignment (VAL) or varus alignment (VAR; Figure 1A). In the central standard position, the axis of the implant stem was aligned with the humeral shaft axis, which was determined using an axis connecting the centers of two circles drawn on the outer cortex at proximal and distal locations. VAL alignment was defined when contact of the distal tip of the humeral stem with the medial cortex endosteum occurred, whereas VAR alignment was defined when contact with the lateral cortex endosteum occurred. Rotation of the implant into the VAL and VAR alignment occurred about an axis in the anterior–posterior direction coincident with the resection plane. Since the implant used in the current investigation permits rotation of the humeral head with respect to the stem, this permitted the use of an identical resection plane for all three stem positions investigated and preserved the central positioning of the most proximal aspect of the stem. The humeral head was intentionally sized and positioned such that contact was achieved on the medial cortex, and no contact was present on the lateral cortex.
Bone was meshed using quadratic tetrahedral elements with a maximum edge length of 2 mm, to comply with the mesh convergence analysis used by Langohr et al.10 To generate both intact (unreconstructed) and reconstructed models with identical bone meshes to permit direct element-to-element comparison of bone stresses, a custom technique10 was used in ABAQUS (Dassault Systemes)whereby a “piece-wise” assembly of partitions in the trabecular bone was generated for each specimen that incorporated the required reamed trabecular geometry for all three humeral implant positions independently without requiring the remeshing of the trabecular bone. This produced both the intact model, with the humeral head and central trabecular bone partitions present, and the humerus model that had been prepared for implant reconstruction with humeral head and central trabecular bone removed. Due to the piece-wise assembly, both models had identical bone meshes for the remaining cortical and trabecular bone in the reconstructed model, which allowed for the direct comparison of each element in the intact prereconstructed humerus model to the corresponding element in the prepared humerus model.
Cortical bone was given a constant modulus of elasticity of E = 20 GPa and Poisson's ratio of ν = 0.3.11, 12 Trabecular bone elements were assigned material properties based on CT attenuation, that varied spatially using a density-modulus relationship of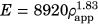 
in which E is the elastic modulus and 
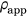is the apparent bone density with a Poisson's ratio of ν = 0.3.13-18 The implant was meshed using quadratic tetrahedral elements, also with a maximum edge length of 2 mm, and assigned material properties of titanium with a modulus of elasticity of E = 110 GPa and a Poisson's ratio of ν = 0.3.10 The three different stem surface features were given appropriate frictional properties where it interacted with the prepared humeral canal: plasma spray (most proximal section, µ = 0.88), grit blast (middle section, µ = 0.63), and polished (most distal section, µ = 0.40). The backside of the humeral head was assigned polished frictional properties (µ = 0.40)19, 20 where it interacted with the resection plane (Figure 1B). Both contact and friction were penalty-based with surface-to-surface discretization.
For both the intact and reconstructed models, the humerus was resected at the mid-diaphysis, and a fixed boundary condition was applied at the resected distal end. A joint reaction force was applied directed towards the center of the humeral head at the articular surface, representing 45° and 75° of abduction, with a magnitude of 440 N for 45° and 740 N for 75°. For both the intact and reconstructed models, the joint reaction forces were applied to the nodes surrounding the load axis where it passed through either the native humeral head or the articular surface of the replacement humeral head for the intact and reconstructed states, respectively. Joint reaction forces were based on in vivo data reported by Bergmann et al.21 who studied shoulder loading using a telemetrized shoulder implant, and a 50th-percentile male body weight of 88.3 kg was assumed.
2.2 Outcome variables and statistical analysis
Four anatomical quadrants (medial, lateral, anterior, posterior) and eight slices parallel to the humeral resection plane for both cortical and cancellous bone, each 5-mm thick, were used to analyze all outcome variables for this study.
To assess the volume-weighted percentage change in bone stress for each reconstructed state versus intact, the resulting difference for each of the six stress components (σ11, σ22, σ33, σ12, σ13, σ23) was calculated. Next, the differential values were passed into the von Mises equation, which yielded a scalar representation of the change in bone stress from pre- to post-reconstruction. While this scalar value does not indicate the directional change of the resulting stress vector, it does reflect the total magnitude of change from the intact state, whereby an ideal scenario is thought to be one in which the reconstructed state exactly mimics the stress of the intact state and any alteration in the bone stress outcome measure is likely less favorable.
The changes in strain energy density (ΔSED) for every element from the intact state to the reconstructed state was also calculated. The expected time-zero bone response (resorb, no change, or remodel) for each element of bone in each slice and quadrant was then estimated using the methodology presented by Neuert et al.22 using a threshold value of 55% change in strain energy density (ΔSED), where a decrease in SED of more than 55% would result in an element being classified as having bone resorption potential, and an increase of more than 55% would result in bone remodeling potential. The resulting elemental response was volume-weighted based on the volume of each individual element.
A four-way (implant position, abduction angle, slice depth, quadrant) repeated measures analysis of variance (RM-ANOVA) with a significance level of α = 0.05 was conducted to assess the change in bone stress and the expected bone response for each implant position investigated. Post-hoc power analysis showed an observed power of 0.8 or greater was achieved for all outcome variables of significance.
3 RESULTS
3.1 Changes in cortical bone stress
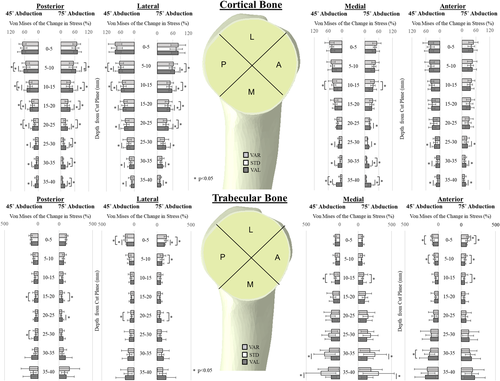
For cortical bone, in the posterior quadrant at depths greater than 5 mm, the valgus position increased the change in bone stress relative to the intact state by an average of 10.8% compared to the standard position (Figure 2, Table 1). Likewise, within the lateral quadrant, at slice depths greater than 5 mm, the valgus position increased the change in cortical bone stress relative to the intact state by an average of 8.1% compared to the standard position (Figure 2, Table 1). In the medial quadrant at slice depths between 20 and 40 mm, the valgus position increased the change in cortical bone stresses relative to the intact state by an average of 10.5% compared to the standard position (Figure 2, Table 1). In the anterior quadrant at slice depths of 25–40 mm beneath the resection plane, the valgus position increased the change in cortical bone stress by an average of 6.5% compared to the standard position (Figure 2, Table 1).
| Depth from cut plane (mm) | Posterior | Lateral | Medial | Anterior | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 45° Abduction | 75° Abduction | 45° Abduction | 75° Abduction | 45° Abduction | 75° Abduction | 45° Abduction | 75° Abduction | |||||||||||||||||
| Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | |
| 0–5 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | ||||||||
| 5–10 | 11.4 | 12.2% | 0.033 | 12.9 | 12.0% | 0.019 | 9.1 | 9.4% | 0.029 | 9.8 | 9.9% | 0.027 | – | – | – | – | – | – | – | – | ||||
| 10–15 | 13.1 | 11.4% | 0.014 | 14.1 | 11.5% | 0.010 | 9.4 | 7.1% | 0.007 | 10.2 | 7.7% | 0.007 | – | – | – | – | – | – | – | – | ||||
| 15–20 | 11.4 | 10.2% | 0.016 | 12.4 | 10.4% | 0.012 | 7.7 | 10.2% | 0.003 | 8.4 | 10.4% | 0.005 | – | – | – | – | – | – | – | – | ||||
| 20–25 | 9.7 | 6.8% | 0.005 | 10.3 | 7.3% | 0.005 | 9 | 6.8% | 0.009 | 9.3 | 7.3% | 0.011 | – | – | 3.1 | 3.6% | 0.045 | – | – | – | – | |||
| 25–30 | 8.5 | 5.8% | 0.005 | 9.7 | 6.4% | 0.004 | 9.9 | 5.8% | 0.035 | 10.4 | 10.4% | 0.025 | 5.8 | 6.2% | 0.032 | 4.7 | 5.3% | 0.044 | 5.9 | 5.6% | 0.021 | 6.0 | 5.1% | 0.013 |
| 30–35 | 8.5 | 6.5% | 0.008 | 10.2 | 7.4% | 0.006 | 5.4 | 4.1% | 0.008 | 6.3 | 3.6% | 0.002 | 9.6 | 9.1% | 0.021 | 10.0 | 9.7% | 0.023 | 6.3 | 5.9% | 0.020 | 6.0 | 4.4% | 0.006 |
| 35–40 | 8.6 | 5.1% | 0.002 | 10.1 | 6.4% | 0.003 | 3.6 | 3.2% | 0.017 | 4.5 | 3.0% | 0.004 | 19.2 | 12.3% | 0.003 | 20.8 | 13.4% | 0.003 | 7.4 | 6.8% | 0.018 | 7.5 | 5.6% | 0.007 |
- Note: Positive values indicate larger changes in stress in the valgus orientation. Dashes indicate that no significant differences were found.
3.2 Changes in trabecular bone stress
In the posterior quadrant at the 20–25 mm slice depth, the valgus position at 75° of abduction increased changes in trabecular bone stress relative to the intact state 21.1% more than the standard position (Figure 2, Table 2). Within the lateral quadrant at the slice depth of 0–5 mm, the valgus position changed the trabecular bone stress 21.9% less than the standard position compared to the intact state, however, this trend changed for the slice depths from 10 to 40 mm, although no statistical significance was detected between the two alignments (Figure 2, Table 2). For the valgus position, in the medial quadrant at slice depths between 30 and 40 mm beneath the resection plane where the distal end of the implant contacted the cortex endosteum, the valgus position significantly increased trabecular bone stress resulting in large negative values reported for change in stress with respect to the intact state compared to the standard position (Figure 2, Table 2).
| Depth from cut plane (mm) | Posterior | Lateral | Medial | Anterior | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 45° Abduction | 75° Abduction | 45° Abduction | 75° Abduction | 45° Abduction | 75° Abduction | 45° Abduction | 75° Abduction | |||||||||||||||||
| Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | |
| 0–5 | – | – | – | – | −22.1 | 17.1% | 0.007 | −21.7 | (16.7)% | 0.009 | – | – | – | – | – | – | – | – | ||||||
| 5–10 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | ||||||||
| 10–15 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | ||||||||
| 15–20 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | ||||||||
| 20–25 | – | – | 21.1 | 24.7% | 0.047 | – | – | – | – | – | – | – | – | – | – | – | – | |||||||
| 25–30 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | ||||||||
| 30–35 | – | – | – | – | – | – | – | – | −97.8 | 111.3% | 0.038 | −117 | 108.8% | 0.021 | – | – | – | – | ||||||
| 35–40 | – | – | – | – | – | – | – | – | −154 | 155.1% | 0.022 | −170 | 149.1% | 0.017 | – | – | – | – | ||||||
- Note: Positive values indicate larger changes in stress in the valgus orientation. Dashes indicate that no significant differences were found.
3.3 Time-zero estimated bone response
Following reconstruction, volumes of cortical and trabecular bone in all quadrants exhibited resorbing potential for all three stem positions. Overall, the valgus position produced the largest volume of bone with resorbing potential compared to the standard and varus positions for all quadrants and slice depths investigated (Cortical: p = 0.033, trabecular: p = 0.012; Figure 3).
3.3.1 Cortical bone response
In the posterior quadrant, valgus implant positioning resulted in 24% more bone volume having resorbing potential compared to the standard position from 5 to 15 mm beneath the resection plane (Figure 3, Table 3). Similarly, in the lateral quadrant valgus implant positioning resulted in 17.2% more bone volume having resorbing potential compared to the standard position from 0 to 30 mm beneath the resection plane (Figure 3, Table 3). Interestingly, in the medial quadrant, valgus implant positioning resulted in 19% less bone volume having resorbing potential compared to the standard position from 0 to 10 mm beneath the resection plane and significantly more bone volume with resorbing potential compared to the standard position from 15 to 20 mm beneath the resection plane (Figure 3, Table 3). Also, in the medial quadrant, varus implant positioning resulted in 13.6% more bone volume with resorbing potential compared to the standard position from 0 to 10 mm beneath the resection plane (0–5 mm: 45° + 16.3 ± 24.6%, p = 0.038; 5–10 mm: 45° + 11.0 ± 16.6%, p = 0.05; Figure 3). Looking at the trends in the anterior quadrant, valgus implant positioning resulted in 20.3% more bone volume with resorbing potential compared to the standard position from 0 to 10 mm beneath the resection plane (Figure 3, Table 3).
| Depth from cut plane (mm) | Posterior | Lateral | Medial | Anterior | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 45° Abduction | 75° Abduction | 45° Abduction | 75° Abduction | 45° Abduction | 75° Abduction | 45° Abduction | 75° Abduction | |||||||||||||||||
| Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | |
| 0–5 | – | – | – | – | 6.2 | 6.6% | 0.034 | 6.6 | 6.9% | 0.031 | – | – | −22.1 | 25.3% | 0.043 | 17.4 | 20.7% | 0.049 | 17.2 | 19.3% | 0.040 | |||
| 5–10 | – | – | 21.3 | 20.6% | 0.019 | 12.4 | 12.1% | 0.024 | 13.2 | 14.7% | 0.039 | −16.9 | 18.8% | 0.043 | −17.9 | 21.7% | 0.024 | 24.6 | 14.8% | 0.002 | 22.2 | 15.5% | 0.005 | |
| 10–15 | 22.3 | 23.5% | 0.032 | 30.1 | 21.8% | 0.006 | 18.0 | 19.2% | 0.034 | 21.6 | 20.3% | 0.019 | – | – | – | – | – | – | – | – | ||||
| 15–20 | – | – | – | – | 12.0 | 9.3% | 0.008 | 24.9 | 22.0% | 0.016 | 7.7 | 6.0% | 0.008 | 7.1 | 5.9% | 0.011 | – | – | – | – | ||||
| 20–25 | – | – | – | – | 20.5 | 12.4% | 0.002 | 22.9 | 10.5% | <0.001 | – | – | – | – | – | – | – | – | ||||||
| 25–30 | – | – | – | – | 26.5 | 26.2% | 0.024 | 21.3 | 23.8% | 0.040 | – | – | – | – | – | – | – | – | ||||||
| 30–35 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | ||||||||
| 35–40 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | ||||||||
- Note: Positive values indicate an increase in resorbing potential in the valgus orientation. Dashes indicate that no significant differences were found.
3.3.2 Trabecular bone response
In the posterior quadrant, valgus implant positioning resulted in 13.7% more bone volume having resorbing potential compared to the standard position from 0 to 20 mm beneath the resection plane (Figure 3, Table 4). Likewise, in the lateral quadrant, valgus positioned implants resulted in 18.5% more bone volume with resorbing potential when compared to the standard position at slice depths from 0 to 25 mm beneath the resection plane (Figure 3, Table 4). Similarly, in the medial quadrant, valgus implant positioning resulted in 6% more bone volume having resorbing potential compared to the standard position from 10 to 20 mm and 30–40 mm beneath the resection plane (Figure 3, Table 4).
| Posterior | Lateral | Medial | Anterior | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 45° Abduction | 75° Abduction | 45° Abduction | 75° Abduction | 45° Abduction | 75° Abduction | 45° Abduction | 75° Abduction | |||||||||||||||||
| Depth from cut plane (mm) | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value | Mean | SD | p-Value |
| 0–5 | 5.4 | 5.0% | 0.019 | 7.2 | 3.9% | 0.001 | 13.0 | 9.1% | 0.005 | 13.9 | 11.4% | 0.011 | – | – | – | – | – | – | 17.9 | 20.7% | 0.045 | |||
| 5–10 | 12.3 | 9.3% | 0.007 | 15.0 | 10.1% | 0.004 | 17.6 | 16.5% | 0.01 | 17.7 | 17.1% | 0.004 | – | – | – | – | – | – | – | – | ||||
| 10–15 | 20.4 | 16.2% | 0.009 | 19.7 | 10.3% | 0.001 | 23.5 | 20.4% | 0.014 | 23.8 | 19.8% | 0.012 | – | – | 7.8 | 8.5% | 0.037 | – | – | – | – | |||
| 15–20 | 15.8 | 18.0% | 0.042 | 14.0 | 12.8% | 0.018 | 20.5 | 20.5% | 0.026 | 20.6 | 20.6% | 0.026 | – | – | 3.3 | 3.8)% | 0.044 | – | – | – | – | |||
| 20–25 | – | – | – | – | 15.5 | 17.7% | 0.042 | – | – | – | – | – | – | – | – | – | – | |||||||
| 25–30 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | ||||||||
| 30–35 | – | – | – | – | – | – | – | – | 4.4 | 3.9% | 0.015 | 4.6 | 3.9% | 0.013 | – | – | – | – | ||||||
| 35–40 | – | – | 10.4 | 5.9% | 0.04 | – | – | – | – | 8.1 | 6.2% | 0.008 | 7.5 | 5.9% | 0.009 | – | – | – | – | |||||
- Note: Positive values indicate an increase in resorbing potential in the valgus orientation. Dashes indicate that no significant differences were found.
4 DISCUSSION
Varus and valgus implant alignment resulting in distal endosteal contact had the largest impact on changes in cortical bone stress in the posterior and lateral quadrants. Valgus alignment produced significantly larger changes in bone stress compared to the intact state than the standard and varus implant alignment at depths greater than 5 mm below the humeral cut plane. There were also many slice depths in these quadrants, particularly in the range of 5–25 mm beneath the humeral cut plane, where the valgus aligned implant altered cortical bone stress more than the varus aligned implant. In the medial quadrant, valgus alignment had the greatest impact on cortical bone stress in the most distal slices, likely a direct result of distal contact of the humeral stem with the medial cortex endosteum.
Similar trends were observed within the trabecular bone where valgus implant alignment produced larger departures in bone stress compared to the intact state than the standard position, with the exception of the most distal slices in the medial quadrant where interestingly the standard position produced significantly larger changes in bone stress compared to the varus position. It is also interesting to note that although the varus aligned implant produced larger departures in bone stress than the standard implant position, significant differences between these two implant positions were only detected in the trabecular bone at 75° of abduction in the most proximal slice.
Valgus implant alignment also produced greater potential for cortical bone resorption than the standard position in the lateral quadrant from 0 to 30 mm, and in the anterior quadrant from 0 to 10 mm beneath the humeral cut plane. This was also found in the posterior and medial quadrants from 10 to 20 mm beneath the humeral cut plane. This may be due to distal contact of the valgus aligned stems with the medial cortex causing direct load transfer distally that unloads the proximal aspect of the humerus. Similar results were observed in trabecular bone, where the valgus implant alignment produced more expected bone resorption than the standard position in most of the slices between 0 and 25 mm beneath the humeral cut plane in the posterior and lateral quadrants, and a variety of slices in the medial and anterior quadrants.
Interestingly, the only locations where valgus alignment produced less expected cortical bone resorption than the standard and varus positions were in the two most proximal slices of the medial quadrant. This trend reversal could be a result of the interaction of the points of load transfer of the valgus and varus aligned stems (Figure 4). The distal aspect of the valgus aligned stem is stabilized by contact with the medial cortex endosteum which prevented movement of the stem in the direction of adduction forming a “bottle opener” effect. In this study, this may have been exacerbated by the absence of humeral head contact with the lateral cortex, resulting in the implant being supported by the less stiff trabecular bone at this location, thereby reducing load transfer laterally. To counteract this, medial contact forces between the backside of the humeral head and the resection plane would have been elevated to counteract the moment produced by the distal stem contact resulting in less medial bone resorption directly beneath the humeral resection plane.
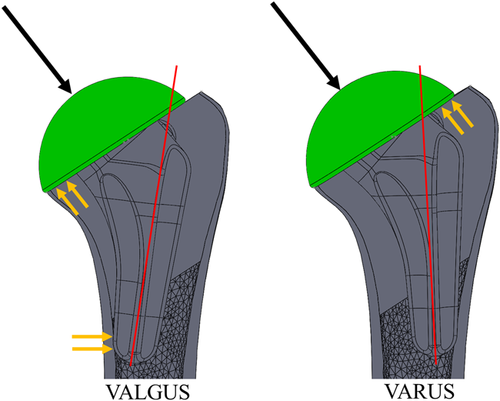
The varus aligned stem is initially stabilized by contact with the lateral cortex endosteum and, in contrast to valgus stem positioning, the distal stem can move freely in the medial direction. The lateral contact between the resection plane and the backside of the humeral head would normally counteract the applied joint reaction force. Since there was no lateral cortical contact, the humeral head subsided slightly into the trabecular bone on the lateral half of the resection surface resulting in the displacement of the distal stem away from the lateral cortex endosteum medially. This may explain why significant differences between the varus and standard positions were not observed in this study.
The results of this study agree with the findings of Peduzzi et al.,9 who investigated stress shielding in 183 patients following TSA with Aequalis Ascend Flex short stems at 2-year follow up. They also found that varus and valgus stem axis deviations increased the risk of bony adaptation, suggesting that implant positioning, in addition to stem filling ratios, may also contribute to stress shielding in humeral short stem components. Although it is important to note that the stem design in their study included a different metaphyseal geometry, which may have also affected the implant-bone load transfer patterns.
The presence of bone resorption potential in all implant positions investigated also agrees with clinical studies that have reported stress shielding in a large proportion of patients. In a study of 73 patients who had received uncemented short stem humeral components with a minimum 2-year follow-up, Casagrande et al.5 found that 71% of shoulders had signs of radiolucency. The causes for humeral loosening and bone resorption were not clear in this study; however, lack of bony on-growth and stress shielding are mentioned as possible causes. Furthermore, although Schnetzke et al.6 reported good clinical outcomes and implant fixation in 82 patients that underwent TSA, they also reported that 13.6% of shoulders had stress shielding and resorption taking place at the medial cortex of the humeral calcar.
The present study has several strengths. Our analysis allowed for direct element-to-element comparison of bone stress and changes in strain energy density between the intact and the reconstructed states, enabling us to detect alterations in the distinct anatomical segments of the humerus. Joint loads were applied representing two distinct abduction angles, in which telemetrized shoulder implant data representative of certain daily tasks was utilized to represent clinically relevant cases. Eight humeri were virtually repeatedly reconstructed with three different stem positions, allowing for the comparison of bone stress between each implant position, something which would have not been achievable using in-vitro cadaveric testing due to the destructive nature of implantation. This allowed for repeated statistical assessments over the population of humeri investigated, which would not have been possible if a single bone model was employed.
This study also has several limitations. The study reports results obtained using data from eight large male cadaveric shoulders which may not permit extension of the results to other patient populations including females and/or severely degenerate shoulders. We only tested two “extreme” positions where endosteal contact occurred, and therefore cannot discuss how less severe varus or valgus stem orientation, which excludes endosteal contact, may impact bone response relative to central positioning. Assumptions made in assigning bone material properties, model boundary conditions, and expected bone response are necessary for computational modeling; and while they may induce error, it is important to note this error is constant throughout all models, and hence the comparison of results following the alteration of implant position are likely to be a direct result of this change in modeling parameter alone. The direction of changes in bone stress compared to the intact state was also not assessed, which means that only changes were detected, and their directions were not reported. Furthermore, the estimates obtained for expected bone response according to change in strain energy density alterations, are obtained immediately following humeral reconstruction, and may not be indicative of long-term bone remodeling since the model is not iterative and does not account for the long-term bone remodeling process. Lastly, the incomplete coverage between the backside of the head and the noncircular resection plane might have altered bone-implant load transfer and amplified the differences measured between the three stem positions. Future investigations should consider varying degrees of humeral head backside contact to assess its impact on humeral bone stress following shoulder arthroplasty.
In conclusion, the results of this study show that central positioning of a short stem humeral implant without any distal cortical contact produces the smallest changes in bone stresses compared to the intact state and the smallest volume of bone expected to resorb due to stress shielding. However, if distal contact must occur, valgus malposition resulting in distal medial stem cortical contact may be worse than varus malposition resulting in distal lateral stem contact in terms of increased changes in bone stress from the intact state, and more bone volume expected to have resorbing potential at the time-zero state resulting in an increased risk of stress-shielding.
ACKNOWLEDGMENTS
The authors would like to acknowledge funding from the Natural Sciences and Engineering Research Council Discovery Grants Program.
CONFLICT OF INTERESTS
The authors Amir Tavakoli, Gregory Spangenberg, Jacob M. Reeves, and G. Daniel G. Langohr, their immediate families, and any research foundations with which they are affiliated have not received any financial payments or other benefits from any commercial entity related to the subject of this article. No financial remuneration to authors or their families was received relating to this article. The author, Kenneth J. Faber, is a consultant for Exactech.
AUTHOR CONTRIBUTIONS
The authors Amir Tavakoli, Gregory Spangenberg, and Jacob M. Reeves had significant contributions to the acquisition, analysis, and interpretation of the research data. The authors Kenneth J. Faber and G. Daniel G. Langohr had significant contributions to the design of the research and the analysis and interpretation of data. All authors had a significant contribution to the drafting, revision, and approval of the submitted version of the manuscript.
