Volume 92, Issue 3 pp. 261-274

ARTICLE

On the clique number of the square of a line graph and its relation to maximum degree of the line graph

Maxime Faron,

Maxime Faron

Department of Computer Science, Ecole Normale Superieure de Lyon, Lyon, France

Search for more papers by this author

Luke Postle,

Corresponding Author

Luke Postle

[email protected]

orcid.org/0000-0002-5023-269X

Canada Research Chair in Graph Theory, Department of Combinatorics and Optimization, University of Waterloo, Waterloo, Ontario, Canada

Correspondence Luke Postle, Department of Combinatorics and Optimization, University of Waterloo, 200 University Ave West, Waterloo N2L 3G1, Ontario, Canada. Email: [email protected]

Search for more papers by this author

Maxime Faron,

Maxime Faron

Department of Computer Science, Ecole Normale Superieure de Lyon, Lyon, France

Search for more papers by this author

Luke Postle,

Corresponding Author

Luke Postle

[email protected]

orcid.org/0000-0002-5023-269X

Canada Research Chair in Graph Theory, Department of Combinatorics and Optimization, University of Waterloo, Waterloo, Ontario, Canada

Correspondence Luke Postle, Department of Combinatorics and Optimization, University of Waterloo, 200 University Ave West, Waterloo N2L 3G1, Ontario, Canada. Email: [email protected]

Search for more papers by this author

First published: 30 January 2019

https://doi.org/10.1002/jgt.22452

Citations: 9

Share a link

Email
Wechat
Bluesky

Abstract

In 1985, Erdős and Nešetřil conjectured that the square of the line graph of a graph 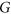$urn:x-wiley:03649024:media:jgt22452:jgt22452-math-0001$ , that is, 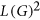$urn:x-wiley:03649024:media:jgt22452:jgt22452-math-0002$ , can be colored with 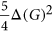$urn:x-wiley:03649024:media:jgt22452:jgt22452-math-0003$ colors. This conjecture implies the weaker conjecture that the clique number of such a graph, that is, 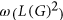$urn:x-wiley:03649024:media:jgt22452:jgt22452-math-0004$ , is at most 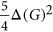$urn:x-wiley:03649024:media:jgt22452:jgt22452-math-0005$ . In 2015, Śleszyńska-Nowak proved that 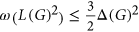$urn:x-wiley:03649024:media:jgt22452:jgt22452-math-0006$ . In this paper, we prove that 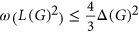$urn:x-wiley:03649024:media:jgt22452:jgt22452-math-0007$ . 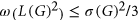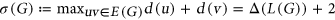This theorem follows from our stronger result that $urn:x-wiley:03649024:media:jgt22452:jgt22452-math-0008$ where $urn:x-wiley:03649024:media:jgt22452:jgt22452-math-0009$ .

REFERENCES

1J. Bang-Jensen et al., On six problems posed by Jarik Nešetřil. In: M. Klazar, J. Kratochvíl, J. Matoušek, R. Thomas, and P. Valtr (eds.), Topics in Discrete Mathematics, Springer, Berlin, Germany, 2006, pp. 615–617.
10.1007/3-540-33700-8_30
Google Scholar
2M. Bonamy, T. Perrett, and L. Postle, Colouring graphs with sparse neighbourhoods: Bounds and applications. arXiv:1810.06704.
Google Scholar
3H. Bruhn and F. Joos, A stronger bound for the strong chromatic index, Combin. Probab. Comput. 27 (2018), no. 1, 21–43.
10.1017/S0963548317000244
Web of Science® Google Scholar
4P. Erdős and J. Nešetřil, Problem. In: G. Halász, and V. T. Sós (eds.), Irregularities of Partitions, Springer, Berlin, Germany, 1989, pp. 162–163.
Google Scholar
5R. J. Faudree et al., Induced matchings in bipartite graphs, Discrete Math. 78 (1989), no. 1-2, 83–87.
10.1016/0012-365X(89)90163-5
Web of Science® Google Scholar
6R. J. Faudree et al., The strong chromatic index of graphs, Ars Combin. 29B (1990), 205–211.
Web of Science® Google Scholar
7M. Molloy and B. A. Reed, A bound on the strong chromatic index of a graph, J. Comb. Theory. Ser. B 69 (1997), no. 2, 103–109.
10.1006/jctb.1997.1724
Web of Science® Google Scholar
8M. Molloy and B. Reed, Graph colouring and the probabilistic method, Springer, Berlin, Germany, 2000.
Google Scholar
9M. Śleszyńska-Nowak, Clique number of the square of a line graph, Discrete Math. 339 (2016), no. 5, 1551–1556.
10.1016/j.disc.2016.01.003
Web of Science® Google Scholar

Citing Literature

Volume92, Issue3

November 2019

Pages 261-274

On the clique number of the square of a line graph and its relation to maximum degree of the line graph

Abstract

REFERENCES

Citing Literature

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On the clique number of the square of a line graph and its relation to maximum degree of the line graph

Abstract

REFERENCES

Citing Literature

References

Related

Information