We have investigated the title question for both a subset of the W4-11 total atomization energies benchmark, and for the A24x8 noncovalent interactions benchmark. Overall, counterpoise corrections to post-CCSD(T) contributions are about two orders of magnitude less important than those to the CCSD(T) interaction energy. Counterpoise corrections for connected quadruple substitutions (Q) are negligible, and ${(Q)}_{\Lambda}-(Q)$ or ${T}_4-(Q)$ especially so. In contrast, for atomization energies, the ${T}_3-(T)$ counterpoise correction can reach about 0.05 kcal/mol for small basis sets like cc-pVDZ, thought it rapidly tapers off with cc-pVTZ and especially aug-cc-pVTZ basis sets. It is reduced to insignificance by the extrapolation of ${T}_3-(T)$ applied in both W4 and HEAT thermochemistry protocols. In noncovalent dimers, the differential BSSE on post-CCSD(T) correlation contributions is negligible even in basis sets as small as the unpolarized split-valence cc-pVDZ(no d).

1 Introduction

Basis set superposition error (BSSE) is the error in the interaction energy between, for example, a dimer AB and its constituent monomers A and B when evaluated in a finite basis set. (At the complete basis set (CBS) limit, BSSE vanishes.) The classic remedy for BSSE is the Boys–Bernardi counterpoise (CP) method [1].

\begin{array}{c}\mathrm{BSSE}=E\left[A\right]+E\left[B\right]-E\left[A(B)\right]-E\left[B(A)\right]\\ {}=E\left[ AB\right]-E\left[A(B)\right]-E\left[B(A)\right]-\left(E\left[ AB\right]-E\left[A\right]-E\left[B\right]\right)\\ {}\begin{array}{c}={D}_e\left[\mathrm{raw}\right]-{D}_e\left[\mathrm{CP}\right]\end{array}\end{array}

(1)

where

{D}_e

denotes the dissociation energy,

E\left[ AB\right]

is the total energy of the dimer,

E\left[A(B)\right]

the total energy of A in the presence of the basis functions on B,

E\left[A\right]

the corresponding total energy in their absence, and so forth.

Inclusion of BSSE in noncovalent interaction (NCI) studies is more or less standard operating procedure, especially in smaller and medium basis sets, as the CP corrections may be on the same order or magnitude as the interaction energies of interest.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Illustration of effect of BSSE on basis set convergence for formic acid dimer. Reprinted from figure 1 in Reference [2], with Creative Commons license.

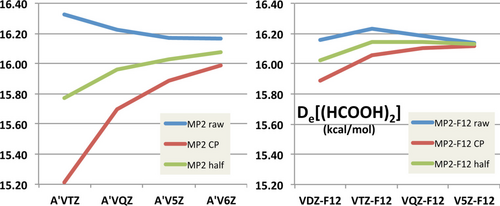
Now it is indeed true that full counterpoise does not guarantee hewing closer to the CBS limit: as shown by Burns, Marshall, and Sherrill [3] for orbital WFT calculations, and by Brauer, Kesharwani, and Martin [2] for explicitly correlated [4-6] F12 calculations, error compensation may take place between BSSE (which always overbinds) and IBSI (intrinsic basis set incompleteness, which almost invariably underbinds). Hence, for small basis sets, complete neglect of BSSE may actually be beneficial, and for medium-size basis sets, “half-counterpoise” (average of corrected and uncorrected interaction energies) tends to offer superior performance [2, 3, 7]. See Figure 1 for an illustration.

In computational thermochemistry, however, the IBSI overwhelms BSSE to such an extent that most researchers make no effort to apply BSSE corrections. This is particularly the case for total atomization energies (TAE), which are the quantum chemical “cognates” of heats of formation

\Delta {H}_f^{\circ }

. The “raw” and CP-corrected TAEs are defined analogously to the NCI situation as (e.g., for a triatomic):

\begin{array}{c} TA{E}_{\mathrm{raw}}\left[\mathrm{ABC}\right]=E\left[A\right]+E\left[B\right]+E\left[C\right]-E\left[\mathrm{ABC}\right]\\ {} TA{E}_{\mathrm{CP}}\left[\mathrm{ABC}\right]=E\left[A\left(\mathrm{BC}\right)\right]+E\left[(A)B(C)\right]+E\left[\left(\mathrm{AB}\right)C\right]-E\left[\mathrm{ABC}\right]\\ {}{\Delta}_{\mathrm{CP}} TA{E}_{\mathrm{CP}}\left[\mathrm{ABC}\right]= TA{E}_{\mathrm{raw}}\left[\mathrm{ABC}\right]- TA{E}_{\mathrm{CP}}\left[\mathrm{ABC}\right]\\ {}=E\left[A\right]+E\left[B\right]+E\left[C\right]-E\left[A\left(\mathrm{BC}\right)\right]-E\left[(A)B(C)\right]-E\left[\left(\mathrm{AB}\right)C\right]\\ {}\end{array}

(2)

where the Wells and Wilson [8] SSFC (site-site function counterpoise) n-body generalization of Equation (1) has been applied. (This effectively amounts to evaluating each atomic energy in the full molecular basis set.)

Higher-accuracy computational thermochemistry protocols like ccCA [9, 10] by the Wilson group, HEAT by the Stanton group [11-14], Weizmann-n by our own group [15-17], and FPD (Feller–Peterson–Dixon, see References [18, 19] and references therein) all entail some variant of basis set extrapolation. If the latter works properly, it ought to eliminate BSSE altogether. (Indeed, we recently [20] exploited this fact to “reverse-engineer” basis set extrapolations.)

Studies of noncovalent interactions, with rare exceptions (such as References [21-23]) stick to the CCSD(T) [24, 25] “gold standard of quantum chemistry” and ignore post-CCSD(T) corrections. However, in thermochemistry, especially for TAEs, it is well-known (see References [11, 26] for early reports) that kJ/mol accuracy cannot be achieved without them. CCSD(T) in fact outperforms the more rigorous CCSDT owing to a well-established error compensation (e.g., References [11, 13, 15, 26]): higher-order triples, ${T}_3-(T)$ , are almost always antibonding, while connected quadruples (Q) are universally bonding.

On the one hand, CCSDT(Q) and especially CCSDTQ have very steep CPU time scalings of $O\left({n}_{\mathrm{occ}.}^4{N}_{\mathrm{virt}.}^5\right)$ and $O\left({n}_{\mathrm{occ}.}^4{N}_{\mathrm{virt}.}^6\right)$ , respectively. On the other hand, these higher-order corrections converge much more rapidly with the basis set than the overall correlation energy [16]. In response to a reviewer comment, we offer Table 1 as an illustration, compiled from data in the supporting information of Reference [28]. The statistics given there cover a 65-molecule subset of the 200-molecule W4-17 thermochemical benchmark [27]; the subset spans a broad range of nondynamical (static) correlation character, from essentially pure dynamical correlation in H₂O and CH₄ at one end, to strong static correlation in O₃, singlet C₂, and BN at the other end. It is clearly seen in Table 1 that RMS contributions taper off rapidly as the connected excitation level increases, to reach insignificance beyond CCSDTQ(5)_Λ. In tandem, it is also seen that basis set convergence becomes ever more rapid, with even unpolarized cc-pVDZ(p, s) yielding surprisingly small errors beyond CCSDT(Q), and ultimately dwindling down into numerical noise.

TABLE 1. Basis set convergence of RMS post-CCSD(T) contributions to the TAEs (kcal/mol) of the 65-molecule W4.3 subset of the W4-17 thermochemical benchmark [27].

	${T}_3-(T)$	$(Q)$	${T}_4-(Q)$	${(Q)}_{\Lambda}-(Q)$	${T}_4-{(Q)}_{\Lambda}$	${(5)}_{\Lambda}$	${T}_5-{(5)}_{\Lambda}$	${(6)}_{\Lambda}$	${T}_6-{(6)}_{\Lambda}$	${T}_7$
nihil	0.84	1.29	0.26	0.17	0.11	0.08	0.015	0.009	0.001	0.001
cc-pVDZ(p, s)	0.53	0.41	0.09	0.07	0.06	0.02	0.003	0.002	0.001	REF
cc-pVDZ(d, s)	0.54	0.25	0.03	0.03	0.01	0.01	REF	REF	REF
cc-pVTZ(f, p)	0.18	0.11	0.012	0.006	0.007	REF	—	—
cc-pVQZ(g, d)	0.09	0.04	REF	REF	REF	—	—	—
cc-pV5Z(h, f)	0.05	0.02
cc-pV{Q, 5} Z	REF	REF

Note: The underlying data were extracted from the ESI of Reference [28], except for the connected sextuples with the cc-pVDZ(d, s) basis set and septuples with the cc-pVDZ(p, s) basis set, which were calculated for the present paper using the general coupled cluster implementation [29, 30] in MRCC [31]; raw energies can be found in the present paper's ESI.

Consequently, post-CCSD(T) corrections tend to be evaluated in very small basis sets, and subsequently applied additively. For instance, in W4 theory [15], the ${T}_3-(T)$ correction is extrapolated from cc-pVDZ and cc-pVTZ basis sets (commonly indicated by the shorthand cc-pV{D, T}Z), the (Q) term is evaluated in a cc-pVTZ basis set, and ${T}_4-(Q)$ in just a cc-pVDZ basis set. (In W4lite theory, just CCSDT(Q)/cc-pVDZ is done for the quadruples.)

This then leads us to the main research question of the present paper: are such corrections materially affected by BSSE corrections? The issue was raised by a reviewer of Reference [23], where we showed that post-CCSD(T) contributions for cohesive energies of water clusters approach 1 kcal/mol for isomers of (H₂O)₂₀.

2 Computational Details

The CCSDT(Q) [32], CCSDT [33], CCSD(T)_Λ [34-37], and CCSD(T) calculations reported in this work were carried out using a combination of the MOLPRO 2024.1 [38], CFOUR [39], and MRCC [31] electronic structure program systems, run on the CHEMFARM cluster of the Faculty of Chemistry at Weizmann. Owing to issues with inconsistent UHF solutions in the presence of ghost atoms, many of the small-molecule counterpoise data were generated using the MRCC interfaces of MOLPRO or CFOUR. For the noncovalent interactions, only closed-shell species are involved, and hence these calculations were carried out using standalone CFOUR (as memory permitted) or MRCC. The latter code was likewise used for some of the additional data in Table 1, using the algorithms presented in References [29, 30].

Reference geometries for the W4-11 thermochemical benchmark [40] (which is a subset of the larger and more recent W4-17 database [27]) were taken from the ESI of the W4-17 paper and used “as is.” Reference geometries for the A24 [21] and S66 [41] datasets were downloaded from the BEGDB database [42] of noncovalent interaction geometries. Using a Python program written by one of us (ES), geometries for A24x8 were generated by compressing or stretching the intermonomer distances by the eight factors {0.9, 0.95, 1.0, 1.05, 1.1, 1.25, 1.50, 2.0} from the familiar S66x8 database [41]. They are provided in the Supporting Information.

For dissociation energies, ${D}_e$ , of diatomic molecules, we applied the standard Boys–Bernardi counterpoise definition. For the TAE_e values (total atomization energies) of small polyatomics, we used the SSFC (site-site function counterpoise) generalization of Wells and Wilson [8].

The basis sets used are of the correlation consistent [43] family, ranging from cc-pVnZ (n = D, T, Q, 5) [44, 45] to aug-cc-pVnZ (n = D, T, Q, 5) [46]. The shorthand cc-pVDZ(d, s) refers to at most d and s functions, respectively, on nonhydrogen and hydrogen atoms (the full cc-pVDZ basis set would correspond to cc-pVDZ(d, p)).

3 Results and Discussion

3.1 Total Atomization Energies

3.1.1 Initial Check for Diatomic Molecules

RMS (root mean square) BSSE corrections for a sample of 24 heavy-atom diatomics and 10 diatomic hydrides are given in Table 2.

TABLE 2. RMS BSSE corrections (kcal/mol) to post-CCSD(T)

{D}_e

contributions for a set of 24 AB and 10 AH diatomics.

	(T)	${(T)}_{\Lambda}-(T)$	${T}_3-(T)$	${T}_3$	$(Q)$	T(Q) − (T)	${(Q)}_{\Lambda}-(Q)$
cc-pVDZ	0.286	0.008	0.043	0.329	0.004	0.045	0.000
cc-pVTZ	0.170	0.005	0.013	0.183	0.006	0.019	0.000
cc-pV{D, T}Z^a			0.008		0.008
cc-pVQZ	0.071	0.002	0.006	0.067	0.003	0.004	0.000
cc-pV5Z	0.034	0.001	0.006	0.028	0.002	0.004	0.000
haVDZ	0.214	0.008	0.026	0.238	0.002	0.026	0.000
haVTZ	0.077	0.003	0.008	0.070	0.004	0.006	0.000
haVQZ	0.037	0.001	0.010	0.028	0.001	0.009	0.000

^a Extrapolation exponents from table 5 of Reference [47].

First of all, unsurprisingly, the effect of BSSE on the difference between CCSDT(Q)_Λ and CCSDT(Q) is less than 0.001 kcal/mol, and can be entirely neglected. For the difference between CCSD(T)_Λ and CCSD(T) we find 0.008 kcal/mol for the cc-pVDZ and haVDZ basis sets, which tapers down to 0.001 kcal/mol for haVQZ and cc-pV5Z.

For connected quadruples (Q), the RMS BSSE is less than 0.01 kcal/mol RMS even with the cc-pVDZ basis set, and smaller still for cc-pVQZ (0.003) and haVQZ (0.001 kcal/mol). We can hence conclude that BSSE on connected quadruples is negligible even for the purposes of high-accuracy work.

The situation for higher-order connected triples ${T}_3-(T)$ , however, is somewhat different. For the cc-pVDZ basis set, we find 0.043 kcal/mol (i.e., 0.18 kJ/mol), which however drops to 0.026 kcal/mol when diffuse functions are added, and to 0.013 kcal/mol when we move things one notch up to cc-pVTZ. Both W4 and HEAT apply cc-pV{D, T}Z extrapolations to the higher-order triples. If we do so here (with extrapolation parameters taken from table V in Reference [47]), the RMS BSSE is just 0.008 kcal/mol, which may be justifiable to neglect in view of other, larger sources of uncertainty such as residual basis set incompleteness in the CCSD(T) component [17]. In fact, for the cc-pV{T, Q}Z basis sets used in W4.3 theory, the BSSE will be even more negligible.

Upon comparing RMS BSSE corrections for (T) and for all of ${T}_3$ (i.e., the difference between CCSDT and CCSD), we note that for smaller basis sets like cc-pVDZ, cc-pVTZ, and haVDZ, there is more BSSE on ${T}_3$ than on (T). For larger basis sets, however, the roles are reversed.

In addition, if one considers the whole CCSDT(Q) − CCSD(T) difference, one finds partial mutual cancelation for BSSE for the larger basis sets, since the differential BSSE effects on ${T}_3-(Q)$ and $(Q)$ pull in opposite directions.

The bottom line for thermochemical applications appears to be that BSSE contributions are negligible for even high-accuracy work. Does this still bear out for polyatomics, or for noncovalent interactions?

3.1.2 Small Polyatomics

While we would not be able to carry out cc-pV5Z, let alone haV5Z CCSDT(Q) calculations on polyatomics, Table 3 presents results with smaller basis sets for a subset of about three dozen triatomics from the W4-11 thermochemical benchmark [40]. Naturally, everything becomes larger in absolute numbers. Nevertheless, the same basic tendencies are seen as for the diatomics:

BSSE on (Q) is basically insignificant and on ${(Q)}_{\Lambda}-(Q)$ wholly so.
BSSE on ${T}_3-(T)$ skirts the 0.1 kcal/mol edge for cc-pVDZ, but tapers down to 0.04 for cc-pVTZ, and becomes negligible with the cc-pV{D, T}Z extrapolation practiced in W4 theory and HEAT.

TABLE 3. RMS BSSE corrections (kcal/mol) to post-CCSD(T) TAE_e contributions for a set of triatomics.

	(T)	${(T)}_{\Lambda}-(T)$	${T}_3-(T)$	${T}_3$	$(Q)$	T(Q) − (T)	${(Q)}_{\Lambda}-(Q)$
cc-pVDZ	0.612	0.018	0.093	0.704	0.008	0.098	0.001
cc-pVTZ	0.353	0.024	0.039	0.389	0.015	0.053	0.003
w/o ClOO	0.353	0.020	0.036	0.388	0.015	0.050	0.002
cc-pV{D, T}Z^a			0.017		0.019
cc-pVQZ	0.143	0.028	0.017	0.139	0.006		0.004
haVDZ	0.443	0.052	0.052	0.487	0.005		0.006
haVTZ	0.171	0.024	0.017	0.168	0.009		0.001

^a Extrapolation exponents from table 5 of Reference [47]. ClOO excluded.

We hence conclude that these thermochemical protocols require no modification to account for post-CCSD(T) BSSE unless one targets an accuracy that is likely unattainable with W4- and HEAT-type approaches.

And once again, substituting haVnZ for cc-pVnZ cuts BSSE in half.

3.2 Noncovalent Interactions

3.2.1 Small Noncovalent Dimers: The A24x8 Dataset

Counterpoise corrections data for the A24x8 dataset are summarized in Table 4.

TABLE 4. RMS BSSE corrections (kcal/mol) to post-CCSD(T)

{D}_e

contributions for the A24x8 set of noncovalent interactions.

	(T)	${T}_3-(T)$	$(Q)$	(T)	${T}_3-(T)$	$(Q)$
	RMS ΔCP			RMS ΔCP/RMS $\Delta {D}_e$
cc-pVDZ(no d)	0.060	0.003	0.004	0.890	0.205	0.239
cc-pVDZ	0.067	0.002	0.003	0.759	0.162	0.208
cc-pVTZ	0.049	0.001	0.003	0.290	0.082	0.134
cc-pVQZ	0.027	0.002		0.127	0.080
haVDZ	0.049	0.002		0.297	0.140
haVTZ	0.016	0.003		0.074	0.147
haVQZ	0.007			0.029
haV5Z	0.003			0.014

Noncovalent interactions are very different in their behavior from atomization energies, in that for most noncovalent complexes, in that MP2 is already a decent to good starting point (except for $\uppi$ -stacking and related). Thus, CCSD-MP2 and (T) are commonly evaluated using relatively small basis sets (see, e.g., References [41, 48] and references therein).

One might thus reasonably expect that post-CCSD(T) contributions will be proportionally much smaller. Admittedly, of course, the A24x8 systems are quite small, and hence post-CCSD(T) contributions might be somewhat less picayune in larger noncovalent complexes, especially at compressed geometries.

The RMS ΔBSSE values are even tinier in absolute terms: 0.002 kcal/mol for ${T}_3-(T)$ and 0.003–0.004 for (Q). For smaller basis sets, these are still nontrivial fractions of the actual $\Delta {D}_e$ contributions. Therefore, any post-CCSD(T) corrections obtained with very small basis sets, such as the unpolarized double zeta cc-pVDZ(no d), need to be regarded with some caution.

For a more reasonable cc-pVTZ basis set, ΔBSSE represents about 8% of the ΔCP [ ${T}_3-(T)$ ] and 13% of Δ(Q).

3.2.2 Not-So-Small Noncovalent Complexes: The S66 Dataset

The aforementioned analysis is open to the criticism that the systems in A24 are quite small and not necessarily representative of what one might see in a real-life application. In contrast, the well-known S66 benchmark [41] consists of dimers of biomolecular building blocks interacting in different ways (hydrogen bonding, $\uppi$ -stacking, pure London dispersion, and mixed-influence). As such, it contains larger systems such as benzene dimer (both parallel-displaced and T-shaped, systems 24 and 47, respectively), uracil dimer (both Watson-Crick 17 and $\uppi$ -stacked 26), pentane and neopentane dimers (systems 34 and 36, respectively).

For this dataset, we will alas have to limit ourselves to the cc-pVDZ(no p on H), a.k.a., cc-pVDZ(d, s), basis set. We were able to obtain full CCSDT BSSE corrections for 64 out of 66 systems, and CCSDT(Q) for about two dozen. (It bears reiterating that, while the dimers often posed memory or computation time requirements that exceeded our available resources, the evaluation of counterpoise corrections does not require the dimers AB, only the monomers in the full dimer basis set A(B) and B(A), as well as naturally the monomers in their own basis set.)

Some relevant statistics can be found in Table 5. Even though with this small basis set, the BSSE correction at the CCSD(T) level is quite hefty, the differential BSSE correction to ${T}_3-(T)$ is surprisingly modest, 0.018 kcal/mol RMS. In fact, the lion's share of even this small difference is recovered at the CCSDT-3 level [49-51]. This approximate coupled cluster approach neglects the ${T}_3$ term in the ${T}_3$ amplitude equations, thus reducing computation time scaling with system size from the $O\left({n}_{\mathrm{occ}.}^3{N}_{\mathrm{virt}.}^5\right)$ of full CCSDT to the same $O\left({n}_{\mathrm{occ}.}^3{N}_{\mathrm{virt}.}^4\right)$ as CCSD(T). (The difference between CCSDT and CCSDT-3 starts in fifth order in many-body perturbation theory [52, 53], with the leading term ${E}_{\mathrm{TT}}^{\left[5\right]}$ . The difference between CCSDT-3 and CCSD(T), on the other hand, has the leading term ${E}_{\mathrm{TQ}}^{\left[5\right]}$ resulting from the action of the disconnected quadruples ${\hat{T}}_2^2/2$ on the connected triples amplitudes ${T}_3$ .)

TABLE 5. RMS BSSE corrections (kcal/mol) to post-CCSD(T)

{D}_e

contributions for the S66 set of larger noncovalent complexes.

Difference	cc-pVDZ(p, s)		cc-pVDZ(d, s)
Difference	RMSDiff(A, B)	${N}_{\mathrm{s} ystems}$	RMSDiff(A, B)	${N}_{\mathrm{s} ystems}$
CCSD–nihil	3.382	66	3.290	66
CCSD(T)–CCSD	0.211	66	0.232	66
CCSDT-3–CCSD(T)	0.013	66	0.018	66
CCSD(T)_Λ–CCSD(T)	0.009	66	0.010	66
CCSDT–CCSD(T)	0.008	66	0.013	64^a
CCSDT–CCSD(T)_Λ	0.007	66	0.006	64
CCSDT–CCSDT-3	0.007	66	0.007	64
CCSDT(Q)–CCSDT	0.007	59	0.008	25
CCSDT(Q)–CCSDT-3	0.011	59	0.014	25
CCSDT(Q)–CCSD(T)	0.003	59	0.005	25

^a Missing S66 systems 41 uracil-pentane and 43 uracil-neopentane.

A still more economical approximation is offered by CCSD(T)_Λ [34-37] which is only $O\left({n}_{\mathrm{occ}.}^2{N}_{\mathrm{virt}.}^4\right)$ in the iterations, followed by a single $O\left({n}_{\mathrm{occ}.}^3{N}_{\mathrm{virt}.}^4\right)$ step. Its cost premium over CCSD(T) is just in the need to also solve for the “left-hand eigenvectors” aside from the CCSD “right-hand” solution (which approximately doubles overall CPU time).

While we admittedly do not have as many data points for (Q) as for ${T}_3-(T)$ , for the available ones the $\Delta \mathrm{CP}$ is just 0.008 kcal/mol RMS. What is more, $\Delta \mathrm{CP}\left[{T}_3-(T)\right]$ and $\Delta \mathrm{CP}\left[(Q)\right]$ have opposite signs (like the underlying contributions) and cancel each other to a large degree. As a result, the cumulative $\Delta \mathrm{CP}\left[\mathrm{CCSDT}(Q)-\mathrm{CCSD}(T)\right]$ is just a measly 0.006 kcal/mol, which can be regarded as negligible by any reasonable standard.

If we remove all polarization functions from cc-pVDZ, we are left with just a split-valence basis set, and most of the CCSDT(Q) calculations come within reach. To our astonishment, we found that the differential BSSEs on ${T}_3-(T)$ , (Q), and CCSDT(Q)–CCSD(T) remain equally tiny.

4 Conclusions

In response to our research question, we can conclude the following:

For high-accuracy computational thermochemistry, particularly total atomization energies obtained at the W4 or HEAT levels, ${T}_3-(T)$ with the cc-pVDZ basis set carries a small but noticeable BSSE.
This is effectively removed, however, by the extrapolation of ${T}_3-(T)$ from cc-pV{D, T}Z basis sets.
BSSE on (Q) may be regarded as negligible in a thermochemistry context.
For noncovalent interactions, BSSE on both ${T}_3-(T)$ and $(Q)$ is insignificant even for basis sets as small as cc-pVDZ, and besides is subject to a degree of mutual cancelation between ${T}_3-(T)$ and (Q).

Author Contributions

M.S. brought on the subject matter. V.F. performed the calculations and curated the data for the TAE BSSE corrections. E.S. carried out the A24x8 calculations and curated the relevant data. E.S. and J.M.L.M. shared the S66 calculations. J.M.L.M. oversaw the project and wrote the first draft, while all authors contributed to the completed manuscript.

Acknowledgments

This work was supported by the Israel Science Foundation (grant 1969/20) and by the Uriel Arnon Memorial Center for AI research into smart materials. J.M.L.M. thanks the Quantum Theory Project at the University of Florida and its head, Prof. John F. Stanton, for their hospitality. The authors would like to thank Drs. Peter R. Franke, Branko Ruscic, and Nisha Mehta as well as Profs. A. Daniel Boese (KFU Graz, Austria) and Leslie Leiserowitz (Weizmann) for inspiring discussions, and Dr. James R. Thorpe and Prof. Devin A. Matthews (Southern Methodist U., Dallas, TX) for fixing a particularly vexing memory allocation bug in CFOUR, thus removing an insurmountable obstacle for the S66 calculations. All calculations were carried out on the ChemFarm HPC cluster of the Weizmann Institute Faculty of Chemistry.

Conflicts of Interest

The authors declare no conflicts of interest.

Open Research

Data Availability Statement

The data that support the findings of this study are available in the Supporting Information of this article.

Supporting Information

References

1S. F. Boys and F. Bernardi, “The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures With Reduced Errors,” Molecular Physics 19, no. 4 (1970): 553–566.
10.1080/00268977000101561
CAS Web of Science® Google Scholar
2B. Brauer, M. K. Kesharwani, and J. M. L. Martin, “Some Observations on Counterpoise Corrections for Explicitly Correlated Calculations on Noncovalent Interactions,” Journal of Chemical Theory and Computation 10, no. 9 (2014): 3791–3799.
10.1021/ct500513b
CAS PubMed Web of Science® Google Scholar
3L. A. Burns, M. S. Marshall, and C. D. Sherrill, “Comparing Counterpoise-Corrected, Uncorrected, and Averaged Binding Energies for Benchmarking Noncovalent Interactions,” Journal of Chemical Theory and Computation 10, no. 1 (2014): 49–57.
10.1021/ct400149j
CAS PubMed Web of Science® Google Scholar
4C. Hättig, W. Klopper, A. Köhn, and D. P. Tew, “Explicitly Correlated Electrons in Molecules,” Chemical Reviews 112, no. 1 (2012): 4–74.
10.1021/cr200168z
PubMed Web of Science® Google Scholar
5L. Kong, F. A. Bischoff, and E. F. Valeev, “Explicitly Correlated R12/F12 Methods for Electronic Structure,” Chemical Reviews 112, no. 1 (2012): 75–107.
10.1021/cr200204r
CAS PubMed Web of Science® Google Scholar
6S. Ten-no and J. Noga, “Explicitly Correlated Electronic Structure Theory From R12/F12 Ansätze,” Wiley Interdisciplinary Reviews: Computational Molecular Science 2, no. 1 (2012): 114–125.
10.1002/wcms.68
CAS Web of Science® Google Scholar
7A. Halkier, H. Koch, P. Jørgensen, O. Christiansen, I. M. Beck Nielsen, and T. Helgaker, “A Systematic Ab Initio Study of the Water Dimer in Hierarchies of Basis Sets and Correlation Models,” Theoretical Chemistry Accounts 97, no. 1–4 (1997): 150–157.
10.1007/s002140050248
CAS Web of Science® Google Scholar
8B. H. Wells and S. Wilson, “van der Waals Interaction Potentials: Many-Body Basis Set Superposition Effects,” Chemical Physics Letters 101, no. 4–5 (1983): 429–434.
10.1016/0009-2614(83)87508-3
CAS Google Scholar
9N. J. DeYonker, T. R. Cundari, and A. K. Wilson, “The Correlation Consistent Composite Approach (ccCA): An Alternative to the Gaussian-n Methods,” Journal of Chemical Physics 124, no. 11 (2006): 114101.
Google Scholar
10C. Peterson, D. A. Penchoff, and A. K. Wilson, “ Prediction of Thermochemical Properties Across the Periodic Table: A Review of the Correlation Consistent Composite Approach (ccCA) Strategies and Applications,” in Annual Reports in Computational Chemistry, vol. 12, ed. D. A. Dixon (Amsterdam, Netherlands: Elsevier, 2016), 3–45.
Google Scholar
11A. Tajti, P. G. Szalay, A. G. Császár, et al., “HEAT: High Accuracy Extrapolated Ab Initio Thermochemistry,” Journal of Chemical Physics 121, no. 23 (2004): 11599–11613.
10.1063/1.1811608
CAS PubMed Web of Science® Google Scholar
12Y. J. Bomble, J. Vázquez, M. Kállay, et al., “High-Accuracy Extrapolated Ab Initio Thermochemistry. II. Minor Improvements to the Protocol and a Vital Simplification,” Journal of Chemical Physics 125, no. 6 (2006): 064108.
10.1063/1.2206789
PubMed Web of Science® Google Scholar
13M. E. Harding, J. Vázquez, B. Ruscic, A. K. Wilson, J. Gauss, and J. F. Stanton, “High-Accuracy Extrapolated Ab Initio Thermochemistry. III. Additional Improvements and Overview,” Journal of Chemical Physics 128, no. 11 (2008): 114111.
10.1063/1.2835612
CAS PubMed Web of Science® Google Scholar
14J. H. Thorpe, C. A. Lopez, T. L. Nguyen, et al., “High-Accuracy Extrapolated Ab Initio Thermochemistry. IV. A Modified Recipe for Computational Efficiency,” Journal of Chemical Physics 150, no. 22 (2019): 224102.
10.1063/1.5095937
PubMed Web of Science® Google Scholar
15A. Karton, E. Rabinovich, J. M. L. Martin, and B. Ruscic, “W4 Theory for Computational Thermochemistry: In Pursuit of Confident Sub-kJ/mol Predictions,” Journal of Chemical Physics 125, no. 14 (2006): 144108.
10.1063/1.2348881
CAS PubMed Web of Science® Google Scholar
16A. Karton, P. R. Taylor, and J. M. L. Martin, “Basis Set Convergence of Post-CCSD Contributions to Molecular Atomization Energies,” Journal of Chemical Physics 127, no. 6 (2007): 064104.
10.1063/1.2755751
PubMed Web of Science® Google Scholar
17N. Sylvetsky, K. A. Peterson, A. Karton, and J. M. L. Martin, “Toward a W4-F12 Approach: Can Explicitly Correlated and Orbital-Based Ab Initio CCSD(T) Limits Be Reconciled?,” Journal of Chemical Physics 144, no. 21 (2016): 214101.
10.1063/1.4952410
PubMed Google Scholar
18D. A. Dixon, D. Feller, and K. A. Peterson, “ Chapter One — A Practical Guide to Reliable First Principles Computational Thermochemistry Predictions Across the Periodic Table,” in Annual Reports in Computational Chemistry, vol. 8, ed. R. A. Wheeler (Amsterdam, Netherlands: Elsevier, 2012), 1–28.
Web of Science® Google Scholar
19D. Feller, K. A. Peterson, and B. Ruscic, “Improved Accuracy Benchmarks of Small Molecules Using Correlation Consistent Basis Sets,” Theoretical Chemistry Accounts 133 (2014): 1407.
10.1007/s00214-013-1407-z
CAS Web of Science® Google Scholar
20V. Fishman, E. Semidalas, and J. M. L. Martin, “Basis Set Extrapolation from the Vanishing Counterpoise Correction Condition,” Journal of Physical Chemistry A 128, no. 35 (2024): 7462–7470.
10.1021/acs.jpca.4c03012
CAS PubMed Web of Science® Google Scholar
21J. Řezáč and P. Hobza, “Describing Noncovalent Interactions Beyond the Common Approximations: How Accurate Is the “Gold Standard,” CCSD(T) at the Complete Basis Set Limit?,” Journal of Chemical Theory and Computation 9, no. 5 (2013): 2151–2155.
10.1021/ct400057w
CAS PubMed Google Scholar
22T. Schäfer, A. Irmler, A. Gallo, and A. Grüneis, “Understanding Discrepancies of Wavefunction Theories for Large Molecules,” 2024, https://arxiv.org/abs/2407.01442.
Google Scholar
23G. Santra, M. Shepelenko, E. Semidalas, and J. M. L. Martin, “Is Valence CCSD(T) Enough for the Binding of Water Clusters? The Isomers of (H₂O)₆ and (H₂O)₂₀ as a Case Study,” 2023, https://arxiv.org/abs/2308.06120.
Google Scholar
24K. Raghavachari, G. W. Trucks, J. A. Pople, and M. Head-Gordon, “A Fifth-Order Perturbation Comparison of Electron Correlation Theories,” Chemical Physics Letters 157, no. 6 (1989): 479–483.
10.1016/S0009-2614(89)87395-6
CAS Web of Science® Google Scholar
25J. D. Watts, J. Gauss, and R. J. Bartlett, “Coupled-Cluster Methods With Noniterative Triple Excitations for Restricted Open-Shell Hartree–Fock and Other General Single Determinant Reference Functions. Energies and Analytical Gradients,” Journal of Chemical Physics 98, no. 11 (1993): 8718–8733.
10.1063/1.464480
CAS Web of Science® Google Scholar
26A. D. Boese, M. Oren, O. Atasoylu, J. M. L. Martin, M. Kállay, and J. Gauss, “W3 Theory: Robust Computational Thermochemistry in the kJ/mol Accuracy Range,” Journal of Chemical Physics 120, no. 9 (2004): 4129–4141.
10.1063/1.1638736
CAS PubMed Web of Science® Google Scholar
27A. Karton, N. Sylvetsky, and J. M. L. Martin, “W4-17: A Diverse and High-Confidence Dataset of Atomization Energies for Benchmarking High-Level Electronic Structure Methods,” Journal of Computational Chemistry 38, no. 24 (2017): 2063–2075.
10.1002/jcc.24854
CAS PubMed Web of Science® Google Scholar
28E. Semidalas, A. Karton, and J. M. L. Martin, “W4Λ: Leveraging Λ Coupled-Cluster for Accurate Computational Thermochemistry Approaches,” Journal of Physical Chemistry. A 128, no. 9 (2024): 1715–1724.
10.1021/acs.jpca.3c08158
CAS PubMed Google Scholar
29M. Kállay and P. R. Surján, “Higher Excitations in Coupled-Cluster Theory,” Journal of Chemical Physics 115, no. 7 (2001): 2945–2954.
10.1063/1.1383290
CAS Web of Science® Google Scholar
30M. Kállay and J. Gauss, “Approximate Treatment of Higher Excitations in Coupled-Cluster Theory,” Journal of Chemical Physics 123, no. 21 (2005): 214105.
10.1063/1.2121589
PubMed Web of Science® Google Scholar
31M. Kállay, P. R. Nagy, D. Mester, et al., “The MRCC Program System: Accurate Quantum Chemistry From Water to Proteins,” Journal of Chemical Physics 152, no. 7 (2020): 074107.
10.1063/1.5142048
CAS PubMed Web of Science® Google Scholar
32Y. J. Bomble, J. F. Stanton, M. Kállay, and J. Gauss, “Coupled-Cluster Methods Including Noniterative Corrections for Quadruple Excitations,” Journal of Chemical Physics 123, no. 5 (2005): 054101.
10.1063/1.1950567
PubMed Web of Science® Google Scholar
33J. Noga and R. J. Bartlett, “The Full CCSDT Model for Molecular Electronic Structure,” Journal of Chemical Physics 86, no. 12 (1987): 7041–7050.
10.1063/1.452353
CAS Web of Science® Google Scholar
34J. F. Stanton and J. Gauss, “A Simple Correction to Final State Energies of Doublet Radicals Described by Equation-of-Motion Coupled Cluster Theory in the Singles and Doubles Approximation,” Theoretica Chimica Acta 93, no. 5 (1996): 303–313.
10.1007/BF01127508
CAS Web of Science® Google Scholar
35T. D. Crawford and J. F. Stanton, “Investigation of an Asymmetric Triple-Excitation Correction for Coupled-Cluster Energies,” International Journal of Quantum Chemistry 70, no. 4–5 (1998): 601–611.
10.1002/(SICI)1097-461X(1998)70:4/5<601::AID-QUA6>3.0.CO;2-Z
CAS Web of Science® Google Scholar
36S. A. Kucharski and R. J. Bartlett, “Noniterative Energy Corrections Through Fifth-Order to the Coupled Cluster Singles and Doubles Method,” Journal of Chemical Physics 108, no. 13 (1998): 5243–5254.
10.1063/1.475961
CAS Web of Science® Google Scholar
37S. A. Kucharski and R. J. Bartlett, “Sixth-Order Energy Corrections With Converged Coupled Cluster Singles and Doubles Amplitudes,” Journal of Chemical Physics 108, no. 13 (1998): 5255–5264.
10.1063/1.475962
CAS Web of Science® Google Scholar
38H.-J. Werner, P. J. Knowles, F. R. Manby, et al., “The Molpro Quantum Chemistry Package,” Journal of Chemical Physics 152, no. 14 (2020): 144107.
10.1063/5.0005081
CAS PubMed Web of Science® Google Scholar
39D. A. Matthews, L. Cheng, M. E. Harding, et al., “Coupled-Cluster Techniques for Computational Chemistry: The CFOUR Program Package,” Journal of Chemical Physics 152, no. 21 (2020): 214108.
10.1063/5.0004837
CAS PubMed Web of Science® Google Scholar
40A. Karton, S. Daon, and J. M. L. Martin, “W4-11: A High-Confidence Benchmark Dataset for Computational Thermochemistry Derived From First-Principles W4 Data,” Chemical Physics Letters 510, no. 4–5 (2011): 165–178.
10.1016/j.cplett.2011.05.007
CAS Google Scholar
41J. Řezáč, K. E. Riley, and P. Hobza, “S66: A Well-Balanced Database of Benchmark Interaction Energies Relevant to Biomolecular Structures,” Journal of Chemical Theory and Computation 7, no. 8 (2011): 2427–2438.
10.1021/ct2002946
CAS PubMed Web of Science® Google Scholar
42J. Řezáč, P. Jurečka, K. E. Riley, et al., “Quantum Chemical Benchmark Energy and Geometry Database for Molecular Clusters and Complex Molecular Systems (www.begdb.com): A Users Manual and Examples,” Collection of Czechoslovak Chemical Communications 73, no. 10 (2008): 1261–1270.
10.1135/cccc20081261
CAS Web of Science® Google Scholar
43T. H. Dunning, Jr., K. A. Peterson, and D. E. Woon, “ Basis Sets: Correlation Consistent Sets,” in Encyclopedia of Computational Chemistry, ed. P. von Ragué Schleyer (New York: Wiley & Sons, 1998).
10.1002/0470845015.cca053
Google Scholar
44T. H. Dunning, Jr., “Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron Through Neon and Hydrogen,” Journal of Chemical Physics 90, no. 2 (1989): 1007–1023.
10.1063/1.456153
CAS Web of Science® Google Scholar
45D. E. Woon and T. H. Dunning, Jr., “Gaussian Basis Sets for Use in Correlated Molecular Calculations. III. The Atoms Aluminum Through Argon,” Journal of Chemical Physics 98, no. 2 (1993): 1358–1371.
10.1063/1.464303
CAS Web of Science® Google Scholar
46R. A. Kendall, T. H. Dunning, Jr., and R. J. Harrison, “Electron Affinities of the first-Row Atoms Revisited. Systematic Basis Sets and Wave Functions,” Journal of Chemical Physics 96, no. 9 (1992): 6796–6806.
10.1063/1.462569
CAS Web of Science® Google Scholar
47A. Karton, “Effective Basis Set Extrapolations for CCSDT, CCSDT(Q), and CCSDTQ Correlation Energies,” Journal of Chemical Physics 153, no. 2 (2020): 024102.
10.1063/5.0011674
CAS PubMed Web of Science® Google Scholar
48B. Brauer, M. K. Kesharwani, S. Kozuch, and J. M. L. Martin, “The S66x8 Benchmark for Noncovalent Interactions Revisited: Explicitly Correlated Ab Initio Methods and Density Functional Theory,” Physical Chemistry Chemical Physics 18, no. 31 (2016): 20905–20925.
10.1039/C6CP00688D
CAS PubMed Web of Science® Google Scholar
49J. D. Watts and R. J. Bartlett, “The Coupled-Cluster Single, Double, and Triple Excitation Model for Open-Shell Single Reference Functions,” Journal of Chemical Physics 93, no. 8 (1990): 6104–6105.
10.1063/1.459002
CAS Web of Science® Google Scholar
50M. Urban, J. Noga, S. J. Cole, and R. J. Bartlett, “Towards a Full CCSDT Model for Electron Correlation,” Journal of Chemical Physics 83, no. 8 (1985): 4041–4046.
10.1063/1.449067
CAS Web of Science® Google Scholar
51J. Noga, R. J. Bartlett, and M. Urban, “Towards a Full CCSDT Model for Electron Correlation. CCSDT-n Models,” Chemical Physics Letters 134, no. 2 (1987): 126–132.
10.1016/0009-2614(87)87107-5
Web of Science® Google Scholar
52S. A. Kucharski and R. J. Bartlett, “Fifth-Order Many-Body Perturbation Theory and Its Relationship to Various Coupled-Cluster Approaches,” Advances in Quantum Chemistry 18 (1986): 281–344.
10.1016/S0065-3276(08)60051-9
CAS Web of Science® Google Scholar
53Y. He, Z. He, and D. Cremer, “Comparison of CCSDT-n Methods With Coupled-Cluster Theory With Single and Double Excitations and Coupled-Cluster Theory With Single, Double, and Triple Excitations in Terms of Many-Body Perturbation Theory—What is the Most Effective Triple-Excitation Method?,” Theoretical Chemistry Accounts 105, no. 3 (2001): 182–196.
10.1007/s002140000196
CAS Google Scholar

Citing Literature

Volume46, Issue1

January 5, 2025

e70006

This article also appears in:

Special Issue to Celebrate Professor Hans Lischka's 80th Birthday

Filename	Description
jcc70007-sup-0001-AppendixS1.zipZip archive, 68.3 KB	Data S1.
jcc70007-sup-0002-TableS1.xlsxExcel 2007 spreadsheet , 98.4 KB	Table S1.
jcc70007-sup-0003-TableS2.xlsxExcel 2007 spreadsheet , 493.2 KB	Table S2.
jcc70007-sup-0004-TableS3.xlsxExcel 2007 spreadsheet , 329.4 KB	Table S3.
jcc70007-sup-0005-TableS4.xlsxExcel 2007 spreadsheet , 2.4 MB	Table S4.
jcc70007-sup-0006-TableS5.xlsxExcel 2007 spreadsheet , 362.5 KB	Table S5.

Does Basis Set Superposition Error Significantly Affect Post-CCSD(T) Corrections?

ABSTRACT

1 Introduction

2 Computational Details

3 Results and Discussion

3.1 Total Atomization Energies

3.1.1 Initial Check for Diatomic Molecules

3.1.2 Small Polyatomics

3.2 Noncovalent Interactions

3.2.1 Small Noncovalent Dimers: The A24x8 Dataset

3.2.2 Not-So-Small Noncovalent Complexes: The S66 Dataset

4 Conclusions

Author Contributions

Acknowledgments

Conflicts of Interest

Open Research

Data Availability Statement

Supporting Information

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Does Basis Set Superposition Error Significantly Affect Post-CCSD(T) Corrections?

ABSTRACT

1 Introduction

2 Computational Details

3 Results and Discussion

3.1 Total Atomization Energies

3.1.1 Initial Check for Diatomic Molecules

3.1.2 Small Polyatomics

3.2 Noncovalent Interactions

3.2.1 Small Noncovalent Dimers: The A24x8 Dataset

3.2.2 Not-So-Small Noncovalent Complexes: The S66 Dataset

4 Conclusions

Author Contributions

Acknowledgments

Conflicts of Interest

Open Research

Data Availability Statement

Supporting Information

References

Citing Literature

Figures

References

Related

Information