Efficient acceleration of the convergence of the minimum free energy path via a path-planning generated initial guess
Abstract
We demonstrate that combining a shifted clustering algorithm with a fast-marching-based algorithm can generate accurate approximations of the minimum energy path (MEP) given a free energy landscape (FEL). Using this approximation as the initial guess for the MEP, followed by further refinement with the string method (referred to as the fast marching tree (FMT)-string combined approach), significantly reduces the number of iterations required for MEP convergence. This approach saves substantial time compared to using linear interpolation (LI) for the initial guess. Our method offers a viable solution for obtaining an effective initial guess of the MEP when an approximate or converged FEL is available. This work highlights the potential of applying FMT-based approaches to extract the MEP in chemical reactions.
1 INTRODUCTION
Analyzing the most probable reaction pathway from reactants to products is a central task in theoretical chemistry. This involves locating transition states (TS) and calculating barrier heights by determining the energy difference between the TS and the reactants to assess the reaction's feasibility.1-7 However, locating the TS is often more challenging than finding the energy minima of stable reactants and products. A common approach involves performing single-point TS optimizations based on an initial TS guess, followed by intrinsic reaction coordinate (IRC) calculations using the converged structure to determine the transition pathway.8-11 Unfortunately, single-point calculations may fail to converge due to the influence of low-frequency modes on the Hessian matrix's quality.
To address this issue, collective variables (CVs) and molecular dynamics (MD) simulations can be used to evaluate the free energy landscape (FEL), locate the TS, and obtain a minimum energy path (MEP). This approach, which relies solely on gradient (force) calculations, is unaffected by low-frequency harmonic modes when evaluating MEPs. Given that reactive processes generally have activation barrier heights greater than , enhanced sampling methods such as umbrella sampling,12-14 metadynamics (MetaD),15-17 replica exchange,18-21 and integrated temperature sampling (ITS)22-24 are employed to overcome activation barriers by biasing the potential energy surface (PES).
There are two distinct methods to obtain a MEP. The first involves guessing an initial string of coordinates and generating structures corresponding to each point on the string. These structures are then used to perform (MD) runs, where the resulting trajectories provide information for modifying the string. Examples of methods in this category include the fly string method,25, 26 finite temperature string (FTS),19, 27, 28 and swarm of trajectories.29-31
In this study, we focus on providing a good initial guess when an approximate or converged FEL is available. To achieve this, we present an efficient approach for obtaining an approximate MEP by utilizing fast-marching-based path planning algorithms.
2 THEORY AND METHODOLOGY
- Initialization: The first step is the stochastic sampling of the points in the free space, where a number , specified by the user, will be randomly selected for path generation. The initial set is created, which includes the initial state and the sampled points. The edge set is initialized as empty, and the sets and are set as and , respectively.
- Neighbor identification: The next step is to generate all the points that have a distance smaller than from the current point , which initially is the starting point .
-
Path exploration: In the third step, for all the points in that are also in :
-
Identify the neighbors of that are within the radius .
-
Find the set of points in that are also in .
-
Determine as the point in that minimizes the cost to come to .
-
-
Edge addition: For each in :
-
If the path from to is collision-free (the path does not cover the obstacle region), add the edge to the tree.
-
Move from to a temporary set .
-
-
Tree update: After all potential connections for the current are explored:
-
Update as .
-
If is empty, return failure as no further expansion is possible.
-
Otherwise, set to be the point in with the minimum cost-to-come.
-
-
Termination: Repeat steps 2–5 until reaches the goal region . Once the goal is reached, return the path from to .
The benefit of FMT is that it always returns a path where the ‘cost’ is minimized given a search radius and converges asymptotically to its global minimum with the increase in the search radius , similar to the scaled hypersphere method.46-49 Additionally, FMT is considered more efficient than FMM due to sampling. Here, we describe how the original 2D FMT algorithm can be modified for path planning to find the initial guess of MEP when there are two CVs.
The first modification is that the map in FMT consists of three-number lists, each containing , which represent the values of , , and the corresponding free energy value instead of and in a typical path planning problem. The second modification is in the collision check process, where a “collision” is confirmed if the straight line connecting two sets of passes through a pair of whose energy is infinite or undefined. Additionally, the search radius, , is defined as the set of points that have the distance less than from a specific point in .
We then present the pipeline for obtaining an MEP from an FEL without any prior guess. The first step is to implement the shifted k-means algorithm to locate the positions of the energy minima. Two inputs are required: the shift and the number of reactants . The shift discards every point with a free energy larger than , so that only the most stable points are clustered with a weight of , where is an even integer.
3 RESULTS AND DISCUSSION
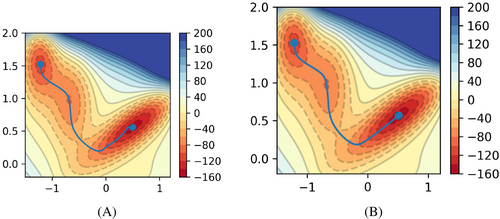
We then compare the number of iterations required to converge a string method calculation using linear interpolation (LI) and the FMT-generated initial guess on model free energy surfaces (FES). The first FES is shown in Figure 1 below. Despite its simplicity, it is a typical FES for an reaction or a hydrogen atom transfer (HAT) reaction that involves bond breaking and bond forming.
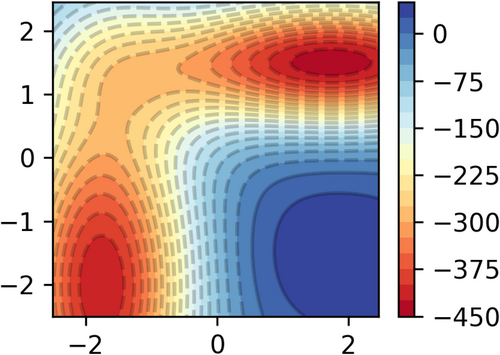
The two energy minima are first identified using the k-means algorithm, storing only points with an energy value less than 400 kJ/mol. The relationship between the matching error and the number of iterations is plotted in Figure 2. Given the estimated barrier height of 100 kJ/mol, the search radius in FMT is set to 10. Since the initial FMT-generated path produces 25 points, the integer multiplier is set to 4, resulting in a string containing 101 nodes. For simplicity, only the first and last nodes will be shown in all the reaction paths in this article. The and gradients of each point on the FEL are evaluated using the “linear” option in scipy for all of the FELs in this article.
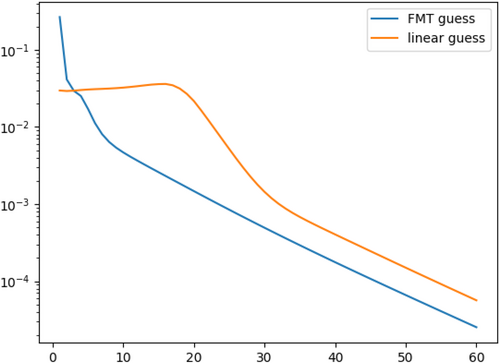
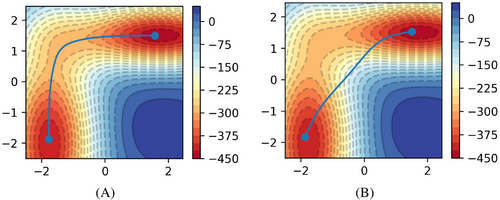
According to the graph, it is clear that the FMT-generated initial guess performs much better than the LI initial guess, as the step length decreases monotonically in the FMT case, while it takes roughly 18 iterations for the LI initial guess to show a similar trend. To achieve a step length of less than 0.01, 24 iterations are required for LI, whereas only 6 are required for FMT. This advantage is further visualized by observing that after 6 iterations, the FMT initial guess-generated MEP is already very close to convergence, unlike the LI case, as shown in Figure 3. Although the decrease in step length is faster in the LI path from iteration 18 to 32, the speed of the drop becomes the same as in the FMT path after that.
To evaluate the computational savings, we measure the compute time required to reduce the step length to be below , , , , and using both LI path and FMT path as the initial guess. In addition to , two other search radii in FMT, namely and , are also experimented with. The computational time to reduce the step length to the aforementioned values, measured in seconds, is shown in Table 1 below.
| Step length | LI (s) | FMT() (s) | % Save | FMT() (s) | % Save | FMT() (s) | % Save |
|---|---|---|---|---|---|---|---|
| 0.01 | 4.171 | 2.744 | 35.2 | 2.017 | 50.9 | 2.680 | 35.7 |
| 0.005 | 4.763 | 3.441 | 25.5 | 2.700 | 41.1 | 3.190 | 33.0 |
| 0.001 | 6.188 | 4.923 | 20.4 | 5.164 | 16.5 | 5.843 | 5.6 |
| 0.0005 | 7.209 | 6.001 | 16.8 | 6.213 | 13.8 | 6.874 | 4.7 |
| 0.0001 | 9.674 | 8.859 | 8.4 | 9.133 | 5.6 | 9.466 | 2.2 |
- Note: All times are measured in seconds.
According to the table, using a combined FMT and string approach requires less time than using the string method alone. The time savings is most prominent when the search radius is 10 and the step length is less than 0.01 due to a relatively optimal choice of and the fact that the FMT-generated initial path is already close enough to the MEP.
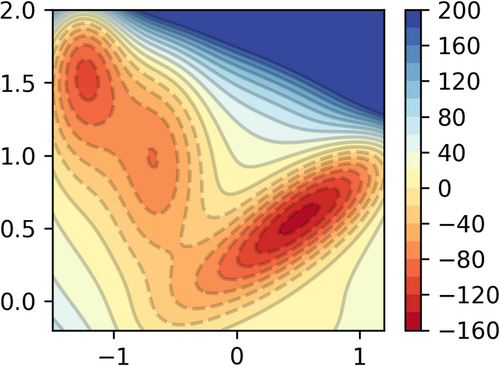
A plot of the potential is shown in Figure 4 below.
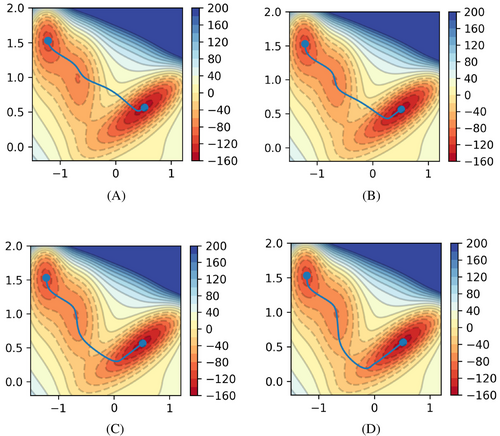
To demonstrate the superiority of the FMT-string combined approach, we plot the evolution of the string using the FMT-generated initial path at the fifth and fifteenth iterations, and the LI initial path at the fifth, fifteenth, twenty-fifth, and thirty-fifth iterations. The plots are shown in Figures 5 and 6 below, and the associated computational costs are outlined in Table 2. The search radius is set to 10, as the estimated barrier height is also 100 kJ/mol. Since the initial FMT-generated path produces 24 points, the integer multiplier is set to 4, resulting in a string containing 97 nodes.
| Iterations | LI (s) | FMT (s) |
|---|---|---|
| 5 | 0.970 | 1.898 |
| 15 | 2.678 | 3.710 |
| 25 | 4.759 | – |
| 35 | 5.893 | – |
According to the figures, it can be observed that the FMT-generated initial path is nearly converged after 5 iterations, with full convergence achieved after 15 iterations, while 35 iterations are required for the LI-generated initial path. This corresponds to a roughly 40% time savings according to the compute time outlined in Table 2.
We finally present an example where there is a competitive pathway, posing difficulties in finding the MEP. In short, a potential well is created in the bottom-right region of the FES in Figure 1, resulting in a competition between two potential paths: the upper and the lower path. The modified FES is shown in Figure 7.
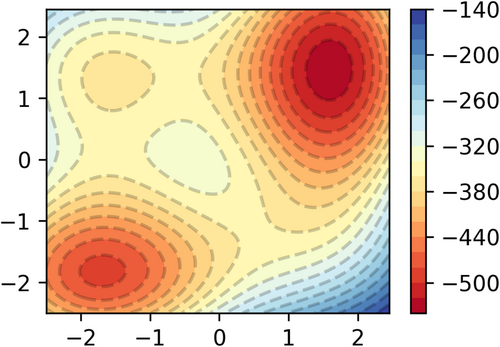
We then compare the evolution of the string using the FMT-generated initial path at 10 and 20 iterations, shown in Figure 8, while that for the LI-generated initial path at 10, 40, 75, and 100 iterations is shown in Figure 9. The search radius is also set to 10. Since the initial FMT-generated path produces 31 points, the integer multiplier is set to 4, resulting in a string containing 125 nodes.
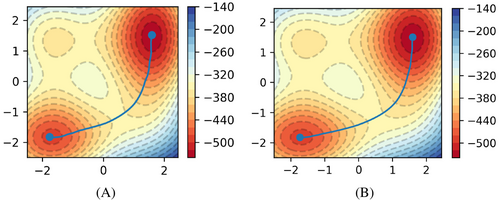
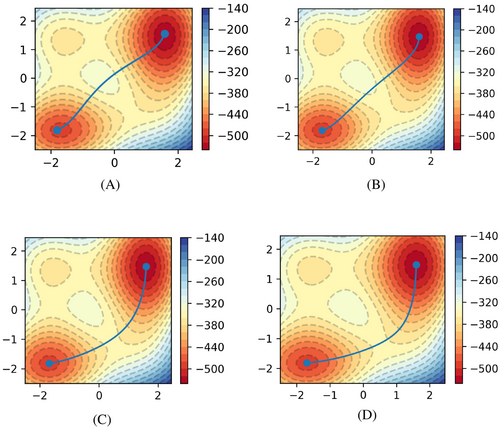
According to the graphs, it is evident that the MEP iterated from an FMT-generated initial guess has nearly converged after 10 iterations, while that iterated from LI does not converge even after 75 iterations. The time cost for the LI and FMT-based algorithms to reach a certain number of iterations is outlined in Table 3. It can be deduced that using an FMT-generated initial guess results in approximately 75% time savings compared to the LI-generated one, as about 20 iterations are required for convergence in the FMT case but around 100 for the LI counterpart. It is also expected that FMT would be able to find a better initial guess and converge faster than LI when the upper path has a lower barrier height than that of the lower path.
| Iterations | LI (s) | FMT (s) |
|---|---|---|
| 10 | 1.976 | 4.186 |
| 20 | 3.984 | 6.117 |
| 40 | 7.937 | – |
| 75 | 16.384 | – |
| 100 | 21.650 | – |
4 CONCLUSION
To summarize, we have presented a novel approach that utilizes a state-of-the-art path planning algorithm, FMT, to generate accurate initial approximations of the MEP. We then coupled this with the string algorithm to further refine the path. Our results from obtaining the MEP of three model (FES) demonstrate that fewer iterations are required to converge the MEP, thus reducing the computational time significantly. This indicates that modern path-finding algorithms can play a pivotal role in efficiently extracting MEPs from complex free energy surfaces.
Future work should focus on applying the FMT-string method to a wider range of chemical reactions to facilitate the search for the MEP. Plausible approaches include initially obtaining an approximate MEP from molecular simulations, then using the FMT-string method to generate a reaction path. Umbrella sampling techniques can subsequently be employed around this path to obtain a more refined reaction pathway, the MEP, and potentially the minimum free energy path (MFEP). Additionally, this method's efficiency should be tested in higher-dimensional FES or PESs. It is also interesting to see how this method is combined with other reaction path optimization methods, such as the MaxFlux method.50-52
The promising results suggest that FMT, combined with the string method, offers a powerful tool for theoretical and computational chemists. By providing efficient and accurate initial guesses, this approach can enhance the study of reaction pathways across a broad spectrum of chemical and biochemical processes.
ACKNOWLEDGMENTS
The author acknowledge the University of Chicago for the teaching assistant fellowship that supports this research. The author also thanks Prof. Gregory Voth, Prof. Lijiang Yang and Fanpeng Meng for valuable discussions.
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.




