2.1 Initial coordinates

For most of the reactive species and transition structures (TSs), the initial Cartesian coordinates (XYZ) were retrieved from previous works.^{23, 27} There were, however, some structures lacking XYZ coordinates for which we built initial molecular models using the Avogadro program.³⁵ To investigate the impact of bifunctional catalysis exerted by ancillary water molecules,^{36, 37} we characterized a series of water-assisted TSs whose initial structures were prepared from those of the counterpart uncatalyzed TSs by performing molecular edition tasks using the Avogadro program.

2.2 Ab initio calculations

All the ab initio calculations were performed with the Dunning's correlation consistent basis sets³⁸ (cc-pVXZ, X = T, Q and 5) for ensuring adequate basis set extrapolation/convergence calculations. For the sake of simplicity, we will use the notation VXZ for referring to the basis sets employed in the various calculations.

In principle, the molecular geometries retrieved from the literature correspond to the most stable and/or most reactive conformers as determined by inspection or by automatic explorations of their potential energy surface (PES). Since extensive conformational searches using high-level ab initio methodologies are still computationally prohibitive and, we just reoptimized those reactive species and TSs on the PES in vacuo at the MP2/VTZ level.³⁹ For each optimized structure, we computed its analytical Hessian to confirm its signature as energy minimum or TS as well as to obtain the harmonic vibrational frequencies. Thermal contributions to the Gibbs energy of the translational, rotational, and vibrational degrees of freedom at 500°C (773 K) and 1 bar were then estimated from the MP2/VTZ moments of inertia and frequencies within the ideal-gas Rigid-Rotor Harmonic-Oscillator (RRHO) approximations. We also note that the lack of conformational averaging most likely has a small effect on the magnitude of the rate-determining Gibbs energy barriers thanks to partial cancelation of entropy effects in the calculation of Gibbs energy differences.

This type of composite approach combining highly-correlated energies with CBS estimations from large basis sets usually provides relative energies within the so-called chemical accuracy (error < 1 kcal/mol).⁴⁴

All the MP2 geometry and frequency calculations were carried out with the Gaussian16 package.⁴⁵ Both the CCSD(T) calculations as well as the MP2/VXZ calculations and the CBS extrapolation were performed with the ORCA 5.0 package.⁴⁶ The frozen core approximation was used in all the MP2 and CCSD(T) calculations.

2.3 Choice of standard state

The translational entropy contribution to $G_{\text{therm}}^{773\mathrm{K}}$ was first evaluated in accordance with the ideal gas-phase standard state (1 bar, 773 K → 0.015 mol/L). This reference state can be termed as a 3D ideal gas state. However, during the fast pyrolysis of cellulose materials or crystalline glucose, the reactive molecules would be most likely confined in a lattice state constituted by a dynamic network of multiple noncovalent interactions with neighboring organic molecules and waters. In this complex scenario, other standard state conventions, such as those defined for molecules adsorbed on a solid surface or on a molecular organic framework may be more adequate. Among the various standard states that have been proposed for the calculation of thermodynamic properties and rate constants for “adsorbed gases,”⁴⁷ we chose the 2D ideal gas convention proposed by Savara³⁴ due to (a) its simplicity (standard coverage σ^o = 1.39·10⁻⁷ mol/m²), and (b) the high temperature during flash pyrolysis (e.g., 773 K) seems compatible with quasi-freely translating molecules throughout the noncovalent framework restraining the reactive molecules. The choice of the standard state is relevant for the kinetic interpretation of the Gibbs energy profiles because, as stated by Laidler,⁴⁸ “if the particular concentrations of interest, which may vary, are chosen as the standard state, then the rate-limiting step is the one of highest Gibbs energy.”

2.4 DFT calculations

For the sake of comparison, all the TSs and minima were recalculated using density-functional-theory (DFT) methodologies. First, we employed the popular B3LYP functional⁴⁹ with the VTZ basis set including also the Grimme dispersion correction⁵⁰ (D3) with the Becke-Johnson damping function. We also carried out geometry optimizations and frequency calculations using the M06-2X DFT functional⁵¹ with the VTZ basis since this DFT method has been intensively used in the former computational studies.

2.5 PCM calculations

To provide a first assessment of non-specific environmental effects, we performed DFT calculations coupled with an implicit solvent model in which the TS/intermediates are embedded within a molecular cavity surrounded by an isotropic dielectric medium.⁵⁴ As suggested in a former computational work,²³ we used the SMD parameterization of the polarizable continuum model (PCM),⁵⁵ which includes both electrostatic and nonelectrostatic (cavity and dispersion) solvation terms, selecting ethanol as the condensed phase because its dielectric constant (ε = 24.852) is close to that of glucose at high temperature. Since the thermochemical conversion of cellulose in supercritical water (SCW) conditions has been previously studied in the frame of hydrothermal carbonization/liquefaction processes,^{56, 57} we also considered SCW conditions. Within the context of the SMD model, we used the parameters proposed by Agrawal et al.⁵⁸ to represent SCW conditions at 723 K and 250 bar (ε = 1.745, refractive index n = 1.086, H-bond acidity = 0.82 and H-bond basicity = 0.35).

All the critical structures were reoptimized at the M06-2X/VTZ SMD-PCM level starting from the gas-phase geometries. Their character as true minima/TSs on the PES were confirmed by the calculation of the M06-2X/VTZ SMD-PCM Hessian matrix. All the SMD-PCM calculations were performed with Gaussian16 using the PCM integral equation formalism⁵⁹ to solve the electrostatic problem of the mutual solute-solvent polarization.

The addition of the ΔG_solv values to the gas-phase Gibbs energies of the reactive species (i.e., $G_{\text{cond}.}=G_{\mathrm{gas}-\text{phase}}+\mathrm{\Delta }{G}_{\text{solv}}.$) allowed us to estimate the Gibbs energy profiles in a condensed phase.

For the SCW conditions, we selected a specific standard state. Thus, the conventional (3D) ideal gas translational entropy included in G_therm was reduced by 8.3 cal mol⁻¹ K⁻¹ to take into account the corresponding decrease in the translational entropy ongoing from the 3D standard state (0.015 M) to the 1 M standard state usually chosen in solution. For water, a pure liquid standard concentration of 6.0 M (ρ = 0.109 g/mL at SCW conditions) was taken.

2.6 Analysis of the reaction paths

To determine the most important pathways from glucose to the HMF/FF products, all the stable intermediates and products were assigned to nodes of a reaction network. Since the size of the examined network was moderate, we enumerated all the simple pathways connecting the first node (glucose) with HMF or FF, assuming that each reaction step can occur in the forward and backward directions and excluding the direct interconversion between HMF and FF. To this end, we employed an Octave script implementing a variant of the shortest path algorithm,⁶⁰ which, determined ~40,000 and ~51,000 possible pathways connecting β-glucoppyranose with HMF and FF, respectively, throughout the reaction network consisting of 54 intermediates and 84 elementary reaction steps. Every pathway was scored first in terms of the relative Gibbs energy of its rate-determining TS at the chosen level of theory. For those pathways presenting the same rate-determining TS, only the shortest one is selected. After applying these conditions (i.e., best Gibbs energy scoring and minimum length), we found that closely related pathways that share more than 2/3 of the intermediate structures were similarly ranked, typically differing by a 1–2 kcal/mol in terms of the stability of the rate-determining TS. Hence, we imposed an additional condition to select other chemically representative pathways by requiring that the fraction of shared structures of a given route with the preceding pathways should be below 2/3. The most representative pathways were automatically tabulated and graphically represented as Gibbs energy profiles using in-house developed scripts. The participation of water molecules as bifunctional catalysts in the reaction paths was considered based on the experimental findings and the previously theoretical justifications reported in the literature. In addition, the use of water molecules to assess the catalytic effect of water release in biomass pyrolysis can also be used to understand the specific role that other OH groups located in other species play in the dehydration reaction paths proposed in our study.

2.7 Availability

The ab initio benchmark calculations reported in this work provide a standardized database of reference structures and energies that can be helpful in developing and validate other computational protocols for the modeling of biomass pyrolysis. For each molecular species, the absolute energies at the different levels of theory, the T1 diagnostics, the Gibbs energy contributions, and the optimized geometries (Cartesian coordinates) are included in Data S3.

3.1 Benchmark calculations

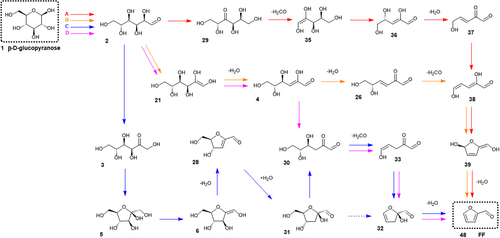
Our survey of the recent literature and careful revision of the theoretical results allowed us to map the landscape of the most relevant mechanisms for the formation of HMF/FF and propose a reaction network including the most relevant structures. This network is fully detailed in Scheme S3. The coordinates of the selected structures have been reported at various levels of theory except those of a few structures for which we obtained de novo coordinates. The assembled network comprises 54 nodes (i.e., stable species) linked through 84 arcs (TSs). As described in Methods, the geometries and Gibbs energies of all the intermediates and TSs were calculated using high-level ab initio methods. From our benchmark results, we identified four different paths throughout the network for the formation of HMF/FF that exhibit similar rate-determining Gibbs energy barriers. These pathways are presented in Schemes 1 and 2 while the corresponding Gibbs energy plots are displayed in Figure 1.

3.2 On the comparison between 2D and 3D standard states

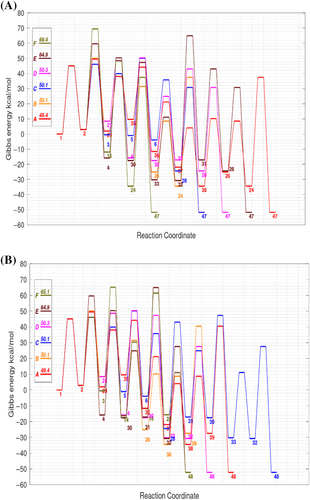
The Gibbs energy profiles shown in Figure 1 were obtained assuming the 2D standard state. This choice can be justified by the flash pyrolysis experimental conditions (i.e., solid reactant, short reaction time, and high heat transfer speed) as well as by the comparable energetics of the concomitant sublimation and pyrolysis processes. The sublimation enthalpy of D-glucose⁶¹ (~46 kcal·mol⁻¹) is not far from the typical activation energies experimentally found in lumped models of pyrolysis of cellulose^62-65 (~45–50 kcal·mol⁻¹), suggesting thus that the key reactions of cellulose/glucose pyrolysis would occur in an environment more similar to that of surface reactions of gases adsorbed on solids at high T (2D) rather than to low-pressure gas-phase conditions (3D). This is in line with the lumped-based kinetic models and the particle-modeling approaches to biomass pyrolysis that implicitly assume complex molecular environments.¹⁹ For example, the most important semi-global (lumped) models include a transformation of cellulose to an “active cellulose” that further undergoes other pyrolysis reactions,^{19, 66} while the heat and transport models inside pyrolyzing particles of biomass combine the kinetic models with the effects due to particle structure and packing, heat transport and diffusion of pyrolysis gases, suggesting thus that many chemical reactions take place on the solid surface of the biomass.

When contrasting the Gibbs energy profiles corresponding to the 2D or 3D standard states (see Figure 1 and Figure S1), the lower translational entropy of the 2D model tends to reduce the entropy gain in Δ_rxnG upon the formation of 2 or more molecules. For example, the Δ_rxnG values for the D-glucose → FF + CH₂O + 2H₂O and D-glucose → HMF + CH₂O + H₂O reactions amount to −52.1 and −51.7 kcal/mol, respectively (2D-ideal gas), and −90.6 and −80.4 kcal/mol (3D ideal gas). Hence, we see that the thermodynamic stability of HMF/FF would be nearly identical in a molecularly crowded environment.

3.3 Mechanistic details of the most favorable pathways

The rate-determining TSs for the reaction mechanisms shown in Schemes 1 and 2 have similar ΔG^‡ values of 49.5–50.3 kcal/mol. Interestingly, both the HMF and FF pathways share the rate-determining TSs, namely TS_2→29, TS_2→21, and TS_5→6. More specifically, the A routes leading to FF/HMF proceed through a series of identical steps (1 → 2 → 29 → 35 → 36 → 37 → 38) followed by either the cyclization of 38 (2,5-dihydroxypenta-2,4-dienal) and subsequent dehydration to give FF, or the direct aldol reaction between the carbonyl group 38 with formaldehyde to give the 26 intermediate, which after a keto-enol rearrangement, results in HMF by alcohol condensation and dehydration. Similarly, the B and C routes to FF/HMF share the 1 → 2 → 21 → 4 → 26 and 1 → 2 → 3 → 5 → 6 → 28 elementary steps, respectively, differing thus in the evolution of 26 and 28 passing through low energy TSs and intermediates.

The routes distinguished in Figure 1 (and in Schemes 1 and 2) are in consonance with the most favorable paths found in the literature. Our route A to FF agrees with the Kang-FF pathway.²⁷ Kang et al.⁶⁷ also identified 2 → 29 as the rate-determining step. The route A is very similar to Zhao-FF. Both routes differ on the pathways proposed to reach the hexulose 29. Regarding HMF, our route A is similar to the Kang-HMF pathway when hydroxymethylation of 38 to 26 is assumed. The viability of aldol reactions in the context of pyrolysis is in agreement with the experimental detection of formaldehyde after the pyrolysis of cellulose.^68-71 The formaldehyde availability is expected to be high since its decomposition (i.e., CH₂O → CO + H₂) presents a very high energy barrier (~79–82 kcal/mol).⁷²

With respect to our B routes, the path toward HMF was substantially studied by Mayes et al.,²³ Kang et al.²⁷ and Hu et al.⁷³ However, only Kang-HMF coincides in the individual steps 21 → 4 → 26 → 24 as the best pathway to achieve HMF. Kang et al.²³ also identified the formation of HHE (21) as the rate-determining step. Concerning FF, our route B combines some steps found in Zhao-HMF and Zhao-FF. Our route C to HMF agrees with Mayes-HMF (the “via fructose” path). Interestingly, these authors also identified 5 → 6 as the rate-determining step along this pathway. Hu et al.⁷³ also explored this path, but it was not the lowest energetic route to HMF. On the other hand, our route C to FF combines some steps found in Mayes-HMF and Hu-FF. The novelty of our pathway is the hydration of the cycloalkene 28. This reaction step is based on the experimental and computational findings presented by other authors about the hydration of species found in the pyrolysis of cellulose.⁷⁴

3.4 Structure of the rate-determining TSs

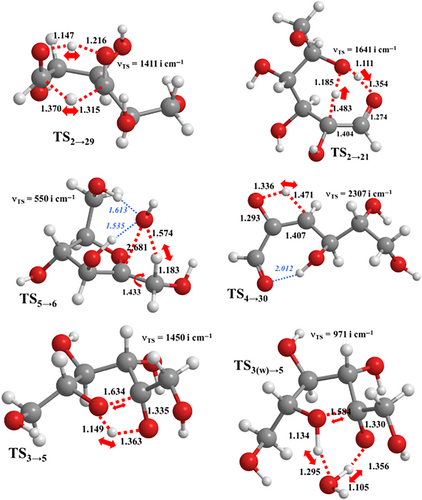
Figure 2 displays the rate-determining TSs for the A–D routes to HMF/FF, which appear at the initial stages of the pyrolytic pathways (subsequent steps can benefit from the entropy gains associated with the release of small molecules). On one hand, TS_2→29 for the rearrangement of D-glucose (2) into L-xylo-3-hexulose (29) is dominated by the double H-transfer from an internal CHOH moiety to the terminal CHO group, the reacting atoms forming a characteristic (and stable) 6-membered ring in which the flying H-atoms constitute nearly-symmetric O···H···O and C···H···C three-center bonds. On the other hand, TS_2→21 for the keto-enol tautomerization of D-glucose into 1,2-didehydro-D-gluco-hexitol (21) is stabilized by the intramolecular catalysis played by the 5-hydroxyl group, which assists the required H-transfer, forming again a 6-membered ring among the reactive centers. Curiously, TS_5→6 for the Macoll 1,2-β dehydration converting the cyclic β-D-fructofuranose species into the cyclic intermediate 6 is a loose TS in which the breaking CO bond is quite elongated (2.6 Å) and the leaving OH moiety gives short H-bond contacts with two hydroxyl groups. Although other Macoll TSs present usually higher energy barriers (e.g., ~60–80 kcal/mol), TS_5→6 is significantly stabilized by specific intramolecular H-bonding effects. The carbon skeleton of TS_4→30, which interconnects electronically conjugated species (tetrahydroxyhex-2-enal (4) and a 1,2-diketo compound 3-depxyglucosone (30)), has only a moderate distortion that can minimize the loss of electronic conjugation. Therefore, these rate-determining TSs are selected not only based on their intrinsic stability (like TS_2→29) but also on the particular effects due to intramolecular catalysis, H-bonding, electronic conjugation, and so on.

3.5 Water catalysis

Bifunctional catalysis by water molecules and other functional groups^{1, 31, 75, 76} can promote H-transfer events in such a way that an O lone pair and an H atom of an appropriately located water molecule (or a nearby hydroxyl group) become involved in the reaction coordinate. Thus, we selected all the TSs having relative ΔG^‡ barrier above 35 kcal/mol (60 out of 83) and we located their water-assisted TS counterparts on the MP2/VTZ PES.

Before presenting the overall impact of water catalysis on the reaction network, it may be interesting to discuss some mechanistic details. For example, Figure 2 displays both the unassisted and water-assisted TSs for the ring closure of the fructose species 3 into the cyclic xylofuranose 30, characteristic of the C routes to HMF/FF. In the absence of ancillary waters, the alcohol group donates its polar H atom to the reactive CO bond forming a 4-membered ring. The H-transfer between these distant centers can be assisted by one water molecule bridging the reactive groups. In this way, the structure of the water-assisted TS_3(w)→5 is clearly less strained (see Figure 2), reducing thus the potential energy barrier. Concerning 3, the electronic energy barrier of TS_3→5, and TS_3(w)→5 amount to 39.6 and 16.7 kcal/mol, respectively. However, the bimolecular character of TS_3(w)→5 implies an entropic penalty accounted for by the ΔG^‡ values of TS_3→5, and TS_3(w)→5 with reference to β-D-glucopyranose, 39.9 and 39.6 kcal/mol, respectively. Although these values certainly depend on the underlying standard state (e.g., 2D ideal gas) as well as on the temperature value (773 K), they point out that the entropic penalty can largely compensate the energetic stabilization achieved by the ancillary water molecular. Similar effects have been recently reported for water-assisted keto-enol rearrangements and retro-Aldol reactions that are not competitive compared with the unassisted steps.⁶⁷ On the other hand, intramolecular catalysis may be more effective than intermolecular catalysis. For example, we found that the keto-enol reaction of D-glucose, 2 → 21, can be assisted by an auxiliary water molecule, resulting in a ΔG^‡ value of 65.5 kcal/mol, which is 15 kcal/mol higher than the equivalent route with intramolecular catalysis. Nevertheless, only a few reaction steps in the reaction network seem compatible with intramolecular catalysis.

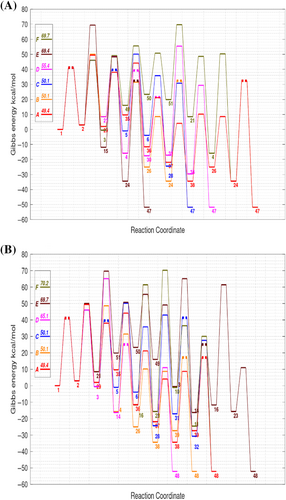
To investigate more systematically the influence of bifunctional catalysis, we rescored each elementary step in the reaction network in terms of the absolute ΔG^‡ barrier at 773 K that has the lower value, either that corresponding to the original (unassisted) TS or that resulting from the water-assisted TS if applicable. The Gibbs energy profiles in Figure 3 confirm that the kinetic role played by water catalysis is quite moderate at the chosen T and standard-state conditions. Thus, the most favorable pathways for the formation of FF/HMF in Figure 1 remain essentially unaltered in Figure 3. They comprise the same intermediate species and only a few steps (e.g., 1 → 2, 24 → HMF, 38 → FF, etc.) become stabilized upon inclusion of the assisting waters. More particularly, the rate-determining TSs and their ΔG values (49–50 kcal/mol) are not modified. Some differences arise when comparing the less stable pathways D–F in Figures 1-3.

3.6 HMF-FF interconversion

As mentioned in Section 2, the search of the pathways connecting β-D-glucopyranose with HMF/FF was carried out considering reversible reaction steps and excluding the direct interconversion HMF → FF + CH₂O. The recent studies by Chen et al.⁷⁷ have shed light on this issue, reporting a high possibility of hydroxymethyl cleavage from HMF leading to FF. This process may occur in a concerted way through TS_HMF→FF for the simultaneous rupture of the exocyclic C₅C₆ bond and H-transfer from the hydroxyl group to the C₅ atom (see Figure S2). Its calculated ΔG^‡ at 773 K is 35.1 kcal/mol with respect to β-D-glucopyranose, which is below those of the rate-determining TSs identified in Figures 1 and 3. Therefore, the direct HMF → FF + CH₂O decomposition may be a viable route in the context of the global Gibbs energy landscape of the reaction network. Nonetheless, TS_HMF→FF is indeed very unstable as measured by its relative energy with respect to HMF (ΔE^‡HMF → TS), which amounts to 92.6 kcal/mol (i.e., electronic energy difference without thermal energy contributions). In fact, other authors have discarded the possibility of the HMF → FF conversion based on the high activation energy of the reaction.^{73, 78}

Considering that water molecules could act as bifunctional catalysts, we computed the water-assisted TSs with one (TS_HMF(w)→FF) and two (TS_HMF(2w)→FF) water molecules (see Figure S2) and found that the ΔG^‡ values with respect to 1 are 25.7 and 33.5 kcal/mol, respectively, again below those of the rate-determining TSs. As expected, the catalytic impact is significant, the corresponding ΔE^‡_HMF→TS being 61.5 and 52.1 kcal/mol. Consequently, the viability of the direct HMF → FF + CH₂O reaction cannot be ruled out, and given that the Δ_rxnG value at 773 K for this process is small (−0.4 kcal/mol), the ratio of the HMF/FF concentrations may be partly determined by pseudo-equilibrium control.

3.7 Environmental effects from solvent continuum models

All the TSs and intermediates were reoptimized using the SMD continuum solvent model as a first approach to incorporate nonspecific environment effects of the Gibbs energy profiles. We obtained all the G values in the continuum (using ethanol parameters) without modifying the reference T (773 K) and standard state convention (i.e., 2D ideal gas). After having ranked again all the glucose → FF/HMF paths, the most important routes are basically coincident both in the gas phase and in the continuum while the rate-determining ΔG^‡ values remain within the 48–50 kcal/mol range. The exact ordering of the A–D pathways depends on the environmental effects, although the changes in the ΔG^‡ values ongoing from gas-phase to the continuum solvent are usually small, ~ ±1–2 kcal/mol. For example, the SMD solvation energy tends to favor the isomerization of β-D-glucopyranose into D-glucose (1 → 2) and that of D-glucose into D-fructose (2 → 3) by 2.3 and 2.4 kcal/mol, respectively, favoring the fructose via.

Application of the SMD methodology with specific parameters for representing SCW may be of interest for hydrothermal pyrolysis. In this case, the low value of the dielectric constant (ε = 1.745) implies a weak electrostatic polarization of the solute molecules, that is, the electrostatic environment would be closer to that of gas phase. In addition, the evaluation of the total G energies under SCW conditions considered a lower T value (723 K) and a different standard state convention as explained in Section 2. After rescoring the glucose → FF/HMF pathways passing through the unassisted thermal TSs, we found that the major A–D pathways match well those in the gas phase (see Figure S4). The addition of the SCW solvation energies increases slightly the rate-determining ΔG^‡ values that range within the 50.5–55.6 kcal/mol interval. Perhaps of further interest is that the fructose routes to HMF and FF, which proceed through the same initial steps, differ in the rate-controlling ΔG^‡ value, 50.6 (HMF) and 53.9 (FF) kcal/mol, showing thus that environmental effects may potentially alter the kinetic preferences for HMF/FF formation. It may be also interesting to note that, in the case of the water-assisted processes, more elementary steps are favored by bifunctional catalysis because the standard concentration of SCW water at 723 K (6.0 M) results in a lower entropy penalty for the solute-water association. However, this effect does not modify substantially the kinetic preferences for the major A–D routes.

3.8 Comparison between benchmark and DFT calculations

Most of the former theoretical results about the pyrolysis mechanisms of D-glucose have been derived from DFT methods, using preferably the M06-2X and B3LYP-D3 functionals. For this reason, we reoptimized all the critical structures at the M06-2X/VTZ and B3LYP-D3/VTZ levels of theory followed by analytical frequency calculations to obtain the corresponding thermal corrections at 773 K.

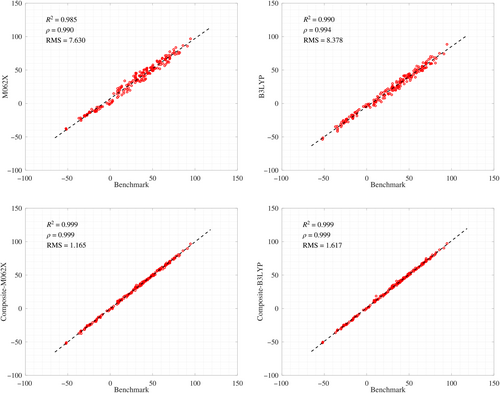
In general, the DFT molecular geometries are very close to the MP2/VTZ ones as characterized by the mean values of the root mean squared differences (RMSD) of the Cartesian coordinates involving C and O atoms: 0.048 and 0.064 Å for the M06-2X/VTZ and B3LYP-D3/VTZ geometries, respectively. More significant differences result when comparing the benchmark ΔG^‡ and Δ_rxnG energies with the DFT values. The degree of agreement depends on the kinetic or thermodynamic character of the Gibbs energies (i.e., ΔG^‡ or Δ_rxnG) and on their absolute or relative character as they are expressed with respect to the common reference [1] or the particular reactant(s) of each elementary step. For example, M06-2X/VTZ predicts ΔG^‡ barriers for the unassisted processes that are much closer to the benchmark values (RMSD = 1.8 kcal/mol) than the B3LYP-D3/VTZ ones (RMSD = 6.1), provided that we compare just the relative ΔG^‡ values (see Table S1). When comparing the absolute ΔG^‡ barriers, the performance of the two DFT levels is more similar (RMSDs = 7.5 and 8.2 kcal/mol). Concerning the prediction of the thermodynamic stability (i.e., relative/absolute Δ_rxnG terms), it turns out that B3LYP-D3/VTZ (RMSDs = 2.3/3.1) outperforms M06-2X/VTZ (RMSD = 3.7/9.4; see Table S1). Focusing on the stability of the water-assisted TSs, the DFT results are worse, particularly those of B3LYP-D3, which systematically underestimates the energy barriers as has been previously reported in the literature.^{1, 21, 25}

The major pathways (A–D) selected by the DFT-based energies are comparable to those predicted by the benchmark calculations (see Table S2). However, the changes in the ΔG^‡ data may influence the interpretation of the results. For example, the ΔG^‡ values for the 30 → 33 and 4 → 30 steps at the M06-2X/VTZ level are about ~5 kcal/mol higher than the benchmark ones, which, in turn, would penalize the formation of FF through the unassisted fructose via with respect to HMF. Curiously, when the water-assisted TSs are considered, the ranking and rate-determining ΔG^‡ of the A–D mechanisms are fairly similar using the M06-2X/VTZ or benchmark energies. On the other hand, the B3LYP-D3/VTZ ΔG^‡ barriers are around 8–10 kcal/mol below the benchmark values and give different rankings of the major pathways. Both M06-2X and B3LYP tend to overestimate the energetic stability of the water-assisted TSs with regard to the unassisted TSs so that the DFT-ranked pathways comprise more water-assisted steps. Therefore, although the DFT calculations point towards similar pathways for the formation of HMF/FF, the DFT energetics can bias the actual kinetic and thermodynamic preferences.

Considering the computational advantages of the DFT methods, we assessed a simple composite protocol aimed at refining the electronic energies through single-point calculations on the DFT geometries. As described in Section 2, the composite-DFT strategy combines the LPNO-CCSD(T)/VTZ energies with the DFT estimation of the CBS limit using only VTZ and VQZ basis sets. These calculations, which have a moderate computational cost, estimate the Gibbs energies in the gas phase in combination with the DFT/VTZ frequencies. Interestingly, the composite-DFT energies are very close to the benchmark values with RMSD values around ~1.0–2.0 kcal/mol. The overall correlation between the composite DFT and benchmark data is excellent (see Table S1 and Figure 4). When assessing the influence of the DFT functional, M06-2X gives, systematically, more accurate composite energies than B3LYP-D3 (e.g., the global RMSD for absolute ΔG is 1.17 (M06-2X) and 1.62 (D3-B3LYP) kcal/mol). The major pathways selected by the composite energies are basically coincident with the benchmark rankings, the changes in the rate-determining ΔG^‡ being around only 1 kcal/mol or lower (see Table S2).

3.9 Comparison with experimental data

The direct comparison between the experimental data generated in the pyrolysis of biomass or cellulose and the results provided by the present benchmark calculations and/or those of former studies is hampered by several factors, such as the neglection (or crude approximation) of environmental effects by conventional QM methods, the incomplete description of catalytic effects, the lack of conformational averaging, and so on. Moreover, other limitations may come from the adoption of a simple criteria for determining the rate-determining step (RDS). In this and other (but not in all) works,³⁰ the RDSs are determined by the TSs of highest Gibbs energy, which implicitly assumes reversible reaction steps and the validity of the steady-state approximation for all the intermediate species.⁷⁹ This choice allows anyway a balanced comparison of the competing mechanisms.

Despite their limitations, our computational results can be addressed against the available experimental evidence, such as the global kinetic parameters obtained in lumped-based modeling. In this regard, our lowest energy routes (A, B, and C) found from β-D-glucopyranose (1) → HMF (47)/FF (48) present ΔG^‡ values ~49.5–50.5 kcal/mol that fit well with the mean value (50.2 kcal/mol) of the experimental activation energies for the pyrolysis of cellulose at 500°C.⁶⁶ It can be noticed, however, that some of the reported results lie in wide intervals (e.g., 48–67 kcal/mol⁶¹ and 44–60 kcal/mol⁸⁰) while other authors give more precise values (e.g., ~46.0 kcal/mol⁶²).

The experimental results of the flash pyrolysis of glucose isotopic labeled with ¹³C indicate that (a) at least 96% of HMF arises in an unimolecular fashion; (b) linear C₄ and C₅ species with a terminus oxygenated function are under compulsion to cyclize forming furans and others⁸¹; (c) the C₅C₆ bond of D-glucose breaks before the cyclization of the linear compounds to FF; (d) C₁ in D-glucose corresponds to the aldehyde group in FF,⁸¹ and (e) the most important source of formaldehyde from D-glucose is C₆.^{27, 73, 82} The routes A, B, and C to FF agree with these observations (e.g., formaldehyde is released from C₆ of D-glucose (2) and C₁ can be identified as the aldehyde group of FF). In addition, the experimental data reveals that the Grob fragmentation should not be the lowest energy path to achieve HMF, thus, highlighting the fructose channel.⁸¹ Our best energy paths A, B, C, and D do not include a Grob fragmentation step. In addition, the C pathway considers D-fructose passing. According to ¹³C NMR experiments, C₁ of D-fructose corresponds to the carbonyl carbon of HMF, and C₆ is the hydroxymethyl carbon of HMF.²⁷ Mechanism C (the only one with D-fructose passing) fits with this observation. About the D-fructose channel, the experimental isotopic results point to preferent dehydration of β-D-fructofuranose by the loss of the OH group at C₂. Our results agree again with this finding as dehydration of 5 → 6 presents a lower ΔG^‡ than 5 → 12.^{72, 81} Finally, it has been suggested that L-xylo-3-hexulose (29) should be involved in FF formation as in the calculated A pathway. Overall, we conclude that our main routes align with isotopic labeling experiments.

Our reaction network is also in consonance with the characterization of the degradation products of lignocellulosic biomass by using tandem mass spectrometry experiments published by Guthrie et al.⁸³ recently. It also agrees the elemental paths and observations presented by Zhou et al.⁸⁴ and Hertzog et al.⁸⁵ based on mass spectrometry, and chromatography and Fourier transform mass spectrometry results, respectively.

Regarding the HMF/FF experimental ratio, Mayes et al.²³ found a molar ratio of ~2.1 when β-D-glucopyranose was pyrolyzed at 773 K with an average particle diameter of 300–500 μm. This ratio has been reported to be ~0.4 when the temperature was 873 K and an average particle diameter of 20 μm.²² From our calculations, the HMF/FF pseudo-equilibrium ratios would be 0.5 (773 K) and 0.2 (873 K). Although the experimental data must be interpreted with caution because of the different conditions, the decrease of the HMF/FF molar ratio with T suggests to hypothesize that the pyrolysis of β-D-glucopyranose to HMF/FF could be under pseudo-equilibrium control. This hypothesis is in line with the experimental results of Wang et al.²² that report a 73% conversion from pure HMF to FF under pyrolytic conditions (873 K). We also calculated the HMF → FF Δ_rxnG at 873 K. The resulting value, −2.5 kcal/mol, corresponds to an HMF conversion percentage of 83% in good agreement with Wang's data.