1 INTRODUCTION

Interfacial phenomena between liquids and electrodes are important in various electrochemical applications, including capacitors and batteries. What is central to these interactions is the electric double layer, where the liquid electrolyte adopts a specific electrostatic orientation, dictating crucial interfacial properties such as stability, conductivity, and reactivity. Theoretical modeling of the electric double layer, spanning over a century and encompassing models such as the Helmholtz, Gouy–Chapman, and Stern models^{1, 2} has provided foundational insights. However, accurately depicting the nanoscale electrostatic potential distribution at the interface is challenging, leading researchers to explore various atomistic simulation studies.^{3, 4}

The electrostatic potential at the interface changes owing to polarization induced by charge-neutral and polar molecules such as water. Furthermore, the interlayer distance between the electrode and ions in the liquid exerts a notable influence, as evidenced by ab initio molecular dynamics (AIMD) studies conducted in aqueous solutions on platinum and graphene electrodes.^{5, 6} Classical molecular dynamics simulations employing empirical potentials with point-charge models have validated these observations, offering simpler yet statistically informed analyses over larger time scales.^7-11 However, both methodologies have difficulties in the tradeoff between computational costs and the applicability of interatomic potentials, posing challenges in further exploring various promising materials.

Graphene oxide (GO) is a promising material for electrical double layer capacitors. While the reduction of GO to graphene enhances conductivity, it also triggers surface recombination, impeding the utilization of the large surface area inherent in chemically exfoliated GO structures.¹² Therefore, the modulation of capacitance via oxidation becomes crucial, although microscopic experimental comparisons are challenging owing to surface changes.^{13, 14} molecular dynamics (MD) simulations employing empirical potentials have elucidated that capacitance changes owing to surface oxidation-induced modifications at the GO–ionic liquid interface.¹⁰ This modeling approach is feasible because it allows the treatment of covalent bonds and partial atomic charges as fixed entities. However, the GO–water system requires a reactive force field owing to the potential interactions between epoxy (–O–) and hydroxyl (–OH) functional groups with water. Proton migration or dissociation of these functional groups into water can occur at the interface, requiring a more intricate modeling approach. Moreover, these complex interactions at the interface are important for a broad array of materials, suggesting the need for a versatile methodology applicable to various species.

While first-principles methods such as AIMD based on density functional theory (DFT) offer comprehensive insights across diverse materials, their computational demands confine their utility to simulations involving a limited number of atoms over short time scales. In contrast, though computationally efficient, classical empirical interatomic potentials are tailored for specific systems developed through fitting for specific elements and structures.

To address the tradeoff between general applicability and computational scalability inherent in conventional interatomic potential approaches, we turn to the newly proposed universal neural network potential (UNNP), such as M3GNet¹⁵ Preferred Potential (PFP)¹⁶ CHGNet¹⁷ or MACE.¹⁸ The UNNP is built on the basis of the neural network potential (NNP),¹⁹ which is one of the emerging methods to approximate DFT potential energy surfaces by neural networks with much less computational cost than DFT.²⁰ The UNNP is an NNP which is applicable for multi-element systems, with an architecture embedding atomic numbers to a graph neural network to cover an arbitrary combination of elements, and it is pre-trained with a large DFT dataset to improve transferability for various structures. It aims to generally reproduce DFT energy and forces across a wide range of materials, encompassing various combinations of elements in the periodic table. The PFP, one notable example of UNNP, can predict the Bader charge of each atom.¹⁶ This charge prediction facilitates integration with electrostatics, as demonstrated in simulations of ion conductivity under an electric field.²¹ In this study, we propose a method to utilize PFP for modeling the interface between liquid and electrode, combining Bader charge prediction with the Coulomb potential arising from an additional charge on the electrodes. Our method involves two key modifications to a standard UNNP simulation. First, to model additional charge on the electrode, we apply a combination of two regions of interatomic potentials, similar to the ONIOM method in QM/MM calculations.²² Second, to correct the long-range interactions in the current UNNP model, we incorporate an additional long-range Coulomb potential calculated using the standard Ewald summation. Our results indicate that this method successfully describes the behavior of graphene–water and GO–water capacitor systems.

2 COMPUTATIONAL METHOD

2.2 Long-range coulomb potential correction for PFP

The Coulomb potential, which is proportional to 1/r (where r is the distance between charges), can influence molecular structures through long-range interactions between distant atoms. Although some NNPs account for long-range interactions,^{27, 28} the PFP employs a more localized interaction model with a 6 Å cutoff, extending up to 22 Å through graph convolution propagation. This range accurately captures the energy and forces of charge-neutral systems, aligning well with DFT calculations without requiring long-range corrections, as demonstrated in previous PFP studies.^{16, 21, 29} However, in systems with charged electrodes, the long-range interactions in liquid (water) molecules can become significant. The Coulomb potential calculated using the Ewald method comprises a short-range term and a long-range term, calculated in real space and k-space, respectively. By adding only the long-range term to the PFP, we can correct the long-range interaction effects, given that the PFP's graph convolution cutoff is 6 Å and its indirect interactions extend to approximately 22 Å. We implemented a method to incorporate the long-range Coulomb term from the Ewald into the PFP, referred to as PFP + long-range. The desired relative error in forces for the Ewald calculation is set to 1e−4 eV/Å.

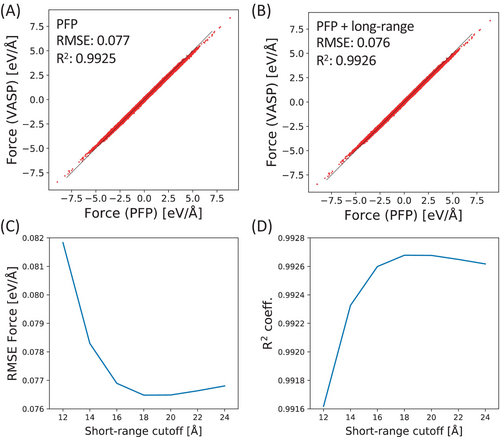
In our MD simulations, we set the short-range cutoff distance to 20 Å, with the long-range correction influencing more distant atoms. We assessed the impact of this correction by comparing the PFP and PFP + long-range results to a DFT dataset for long-range interactions among water molecules. This dataset was taken from a previous study on a long-range corrected NNP.²⁸ Figure 1A,B illustrate the performance of PFP and PFP + long-range, respectively. Both potentials show excellent agreement with the DFT dataset, and the long-range correction using the Ewald method does not result in an increase in average error values or a decrease in the R² coefficient; in fact, the indicators are slightly improved. Figure 1C,D depict the dependence of root mean square error (RMSE) and R² coefficient on the short-range cutoff distance for PFP + long-range. These figures indicate an optimal range for the short-range cutoff of the Ewald correction. A short-range cutoff of 18–20 Å demonstrates good performance, validating our choice of a 20 Å cutoff for MD calculations.

2.3 MD simulation model

Figure 2A shows the structure of the model capacitor system with water between graphene electrodes. The initial distance between the graphene walls is set to 5 nm. Water molecules are placed at regular intervals, with the distance between the graphene layers being 0.33 nm. Water molecules constitute segment A, with potentials and atomic charges predicted by PFP or PFP corrected by the long-range Coulomb potential (PFP + long-range, see the subsequent subsection). The AIREBO potential³⁰ is used for C–C interactions between graphene atoms. The Lennard-Jones potential for water–carbon interaction³¹ is used for CO interactions (σ_CO = 3.190 Å, ϵ_CO = 0.0032 eV). The Coulomb potential for interactions between additional charges and water molecules is calculated within V_B. Additional charges of ±q elemental charge per atom are applied to the C atoms in the graphene layer in contact with water. Figure 2B shows the structure of the model capacitor system with water between GO electrodes. The graphene layer is functionalized with epoxy and hydroxyl groups, with a C:O atom ratio of 4:1 and 1/3 of the functionalization being epoxy groups. The amorphous functionalized structure of GO follows the previous MD simulation literature.³² Water molecules and functional groups on the GO form segment A, to which PFP + long-range is applied. PFP and Coulomb potentials among segment A atoms and additional charges on the C atoms in the GO layer in contact with water are considered in V_B. Covalent interactions between segments A and B are included in these potentials. It is important to note that the charge of the carbon structure in GO is not included in the charges of segment B; only the additional charge ±q is considered for the Coulomb potential.

3 RESULTS AND DISCUSSION

Figure 3A shows the voltage results of the water–graphene electrode under different electrode charge conditions, q = 0.0 and 0.001 e/atom, using PFP for water interaction, where e represents the elementary charge. While the result with q = 0 yields a flat profile of electric field and voltage in the middle between the electrodes, the result with q = 0.001 shows a steady decrease in voltage, reaching less than −30 V at the anode. This inverse modulation of voltage with charge contrasts with the expected behavior, where a positively charged electrode should exhibit a positive voltage, consistent with previous studies⁸ and our validation using SPC/E or TIP3P water models (Figure S2).

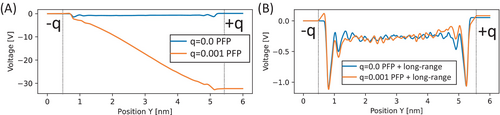
Conversely, the voltage profile calculated using PFP + long-range successfully demonstrates the polarization of H₂O molecules on the graphene electrode interface. Figure 3B depicts the voltage profile results using PFP + long-range for water interaction. The voltage exhibits a profile similar to those in previous studies and our validation, with a flat voltage in the middle and modulation of positive voltage on the anode side. These findings suggest that the localized interaction in PFP (limited to approximately 22 Å) may not fully balance with the long-range Coulomb interaction between additional charges and water partial charges. Thus, the long-range correction to PFP can be achieved through the PFP + long-range method. The difference of these profiles of electrostatic potential shows the importance of the long-range Coulomb interaction within water molecules, particularly when the electrode is charged. This suggests that the long-range Coulomb potential should be considered in other interatomic potentials in the MD simulations including liquid-electrode interfaces.

Figure 4A,B illustrate the number density of O and H atoms in the PFP water simulation along the y coordinate on the cathode and anode, respectively. The distribution of H atoms increases with charge on the cathode and decreases on the anode, while the distribution of O atoms shows little variation with charge. The orientation of water molecules at the interface induces polarization. However, this polarization appears excessively pronounced, leading to the observed excessive modulation of voltage shown in Figure 3A. On the other hand, Figure 4C,D show the results of the PFP + long-range water simulation, which exhibits a much less pronounced but still noticeable degree of polarization with a similar trend. This polarization of charge-neutral water molecules demonstrates the fundamental effect of the electrical double layer in this system.

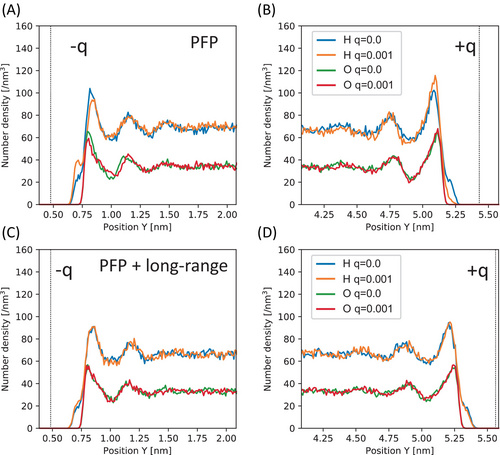
Figure 5 shows the voltage profile of the GO–water interface obtained from our MD simulation at 350 K. With q = 0.001, the voltage on the anode increased by approximately 4 V compared to q = 0, a significantly larger modulation than that observed in the graphene case illustrated in Figure 3B. The polarization of water on the GO interface was less pronounced than that on the graphene interface, indicating that the oxide electrode may provide a smaller capacitance owing to interactions with the surface O and H atoms on the electrode.

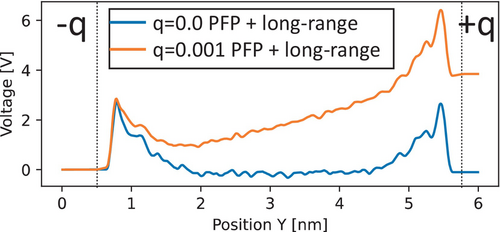
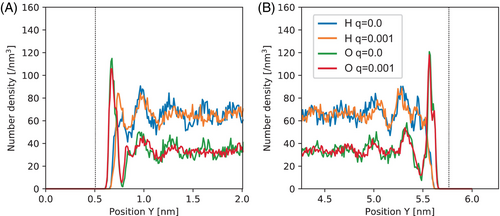
Figure 6 shows the number density of O and H atoms in the GO–water system. The distribution of H atoms increases near the cathode and decreases near the anode with q = 0.001, compared to q = 0, mirroring the modulation observed in graphene. However, the shift in number density is more pronounced in the GO electrode than in graphene. This suggests that the interaction between O and H in the functional group on GO was influenced by the introduction of an additional charge. Interestingly, the modulation of number density appears more pronounced in the GO electrode than in graphene, indicating a weakening of the total polarization by water.

4 CONCLUSION

In this study, we developed a method to incorporate Coulomb interaction into UNNP, enabling simulations of liquid–electrode interfaces. MD simulations were performed for capacitor systems comprising graphene and GO–water interfaces. Our findings revealed that PFP, a UNNP with finite interatomic interaction distances, inadequately describes interface polarization and voltage profiles. To address this limitation, we introduced PFP + long-range, augmenting PFP with long-range electrostatic energy to correct for the influence of long-range Coulomb potential. With PFP + long-range, accurate calculation of electrostatic potential is achievable, even when the charge is injected. Additionally, we observed that GO–water interfaces exhibit weaker polarization compared to graphene electrodes, underscoring the effectiveness of our method for systems featuring covalent bonds at interfaces. These applications underscore the validity of our approach across interfaces with various interfacial interactions, encompassing covalent, ionic, and dispersion bonds, as well as the polarization of neutral molecules. This provides valuable insights into the atomistic mechanisms underlying electrical double layers.