RESEARCH ARTICLE

Open Access

Extended benchmark set for lattice parameters of inorganic solids

Elodie Fernandes Lima

Mulliken Center for Theoretical Chemistry, Clausius-Institute of Physical and Theoretical Chemistry, University of Bonn, Bonn, Germany

Search for more papers by this author

Thomas Bredow,

Corresponding Author

Thomas Bredow

[email protected]

orcid.org/0000-0003-4077-5428

Mulliken Center for Theoretical Chemistry, Clausius-Institute of Physical and Theoretical Chemistry, University of Bonn, Bonn, Germany

Correspondence

Thomas Bredow, Mulliken Center for Theoretical Chemistry, Clausius-Institute of Physical and Theoretical Chemistry, University of Bonn, Beringstr. 4, D-53115 Bonn, Germany.

Email: [email protected]

Search for more papers by this author

Elodie Fernandes Lima,

Elodie Fernandes Lima

Mulliken Center for Theoretical Chemistry, Clausius-Institute of Physical and Theoretical Chemistry, University of Bonn, Bonn, Germany

Search for more papers by this author

Thomas Bredow,

Corresponding Author

Thomas Bredow

[email protected]

orcid.org/0000-0003-4077-5428

Mulliken Center for Theoretical Chemistry, Clausius-Institute of Physical and Theoretical Chemistry, University of Bonn, Bonn, Germany

Correspondence

Thomas Bredow, Mulliken Center for Theoretical Chemistry, Clausius-Institute of Physical and Theoretical Chemistry, University of Bonn, Beringstr. 4, D-53115 Bonn, Germany.

Email: [email protected]

Search for more papers by this author

First published: 12 August 2024

https://doi.org/10.1002/jcc.27479

Citations: 3

Share a link

Email
Wechat
Bluesky

Abstract

The development of novel methods in solid-state quantum chemistry necessitates reliable reference data sets for their assessment. The most fundamental solid-state property of interest is the crystal structure, quantified by the lattice parameters. In the last decade, several studies were conducted to assess theoretical approaches based on the agreement of calculated lattice parameters with respect to experiment as a measure. However, most of these studies used a limited number of reference systems with high symmetry. The present work offers a more comprehensive reference benchmark denoted as Sol337LC, which consists of 337 inorganic compounds with 553 symmetry-inequivalent lattice parameters, representing every element of the periodic table for atomic numbers between 1 and 86, except noble gases, the radioactive elements and lanthanoids. The reference values were taken from earlier benchmarks and from measurements at very low temperature or extrapolation to 0 K. The experimental low-temperature lattice parameters were then corrected for zero-point energy effects via the quasi-harmonic approximation for direct comparison with quantum-chemical optimized structures. A selection of standard density functional approximations was assessed for their deviations from the experimental reference data. The calculations were performed with the crystal orbital program CRYSTAL23, applying optimized atom-centered basis sets of triple-zeta plus polarization quality. The SCAN functional family and the global hybrid functional PW1PW, augmented with the D3 dispersion correction, were found to provide closest agreement with the Sol337LC reference data.

1 INTRODUCTION

The accurate determination of lattice parameters is an important prerequisite for the quantum-chemical calculation of other solid-state properties. These parameters also play a crucial role in predicting and rationalizing various physical and chemical phenomena, including mechanical stability, electronic structure, and reactivity. Therefore an assessment of the accuracy of quantum-chemical methods for predicting crystal structure parameters is indispensable. In the past years, numerous benchmark studies have been performed for a large variety of functionals using the deviation of calculated lattice parameters with respect to experimental reference data as a measure. The dataset of Kresse et al.¹ consists of 30 compounds. The Sol58LC reference set of Perdew et al.² extended this data set to 58 compounds. Both datasets were restricted to compounds in the cubic crystal system. More recent reference sets compiled by Wellendorff et al.,³ Pernot et al.,⁴ Tran et al.,⁵ Truhlar et al.,⁶ Gruneis et al.,⁷ Zhang et al.,⁸ and Xiaofei et al.⁹ are only slightly extended, see Table 1. The selection of reference compounds varies between the benchmark sets (see Tables S1 and S2 in the Supporting Information).

TABLE 1. Literature benchmark studies for the quantum-chemical calculation of solid-state properties sorted by publication year.

Year	Authors	Compounds	LPs	DFAs	Program	Citation
2011	Kresse et al.	120	30	4	VASP (PW)	1
2012	Perdew et al.	58	58	5	BAND (PW)	2
2014	Wellendorff et al.	153	58	14	GPAW (PW)	3
2015	Pernot et al.	28	28	18	CRYSTAL14 (LCAO)	4
2016	Tran et al.	71	44	63	WIEN2k (PW+LO)	5
2017	Truhlar et al.	175	47	10	VASP (PW)	6
2018	Gruneis et al.	14	14	12	VASP (PW)	7
2018	Zhang et al.	64	64	6	VASP (PW)	8
2023	Xiaofei et al.	90	53	6	VASP (PW)	9
	This work	337	553	13	CRYSTAL23 (LCAO)

Note: The total number of inorganic compounds (which are also used for the assessment of other properties), the number of lattice parameters (LP), density functional approximations (DFA), and the applied software are given. PW denotes plane-wave basis, LCAO atom-centered basis functions, LO localized orbitals.

A rather large dataset was compiled by Kingsbury et al.¹⁰ by collecting data from three material data bases, namely Materials Project,¹¹ NOMAD¹² and OQMD.^{13, 14} However, this dataset was excluded from the above list since unit cell volumes rather than individual lattice parameters were considered, and the reference data are obtained from quantum-chemical calculations.

In the present study we compiled a more comprehensive benchmark dataset compared to those listed in Table 1 representing every element of the periodic table for atomic numbers between 1 and 86, except noble gases, the radioactive elements and lanthanoids. At least five compounds per element were selected (see Figure 1) in order to provide at least a minimal basis for statistical analysis, Hg being the only exception. The complete list of reference compounds per element is shown in Table S3 in the Supporting Information. Our intention was to enable an element-specific evaluation of new quantum-chemical methods that may be element-dependent, and of atom-centered basis sets. For most elements except the most common, the selection was only limited by the amount of available experimental data.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Total number of compounds per element in the Sol337LC dataset.

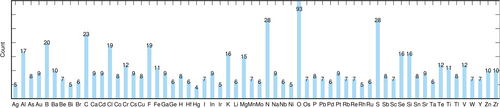
Additionally, the restriction to cubic and hexagonal crystal classes was lifted. It was assumed that potential weaknesses of novel theoretical approaches or basis sets become more visible in less symmetric systems. Therefore compounds of all seven crystal classes are present in the Sol337LC set, see Table 2. Again the number of compounds in each crystal class was only limited by the amount of available experimental data.

TABLE 2. Crystal system, space group (SG) number and Hermann–Mauguin symbol, number of compounds in the Sol337LC benchmark dataset.

Crystal system	SG no.	SG symbol	Compounds	Crystal system	SG no.	SG symbol	Compounds
Triclinic	2	$P \bar{1}$	1	Trigonal	148	$R \bar{3}$	2
Monoclinic	12	$C 2 / m$	2		152	$P 3_{1} 21$	6
	13	$P 2 / c$	1		154	$P 3_{2} 21$	1
	14	$P 2_{1} / c$	8		159	$P 3_{1} c$	1
	15	$C 2 / c$	3		160	$R 3 m$	1
Orthorhombic	41	$A b a 2$	3		161	$R 3 c$	3
	44	$I m m 2$	1		164	$P \bar{3} m 1$	6
	60	$P b c n$	1		166	$R \bar{3} m$	8
	61	$P b c a$	1		167	$R \bar{3} c$	7
	62	$P n m a$	21	Hexagonal	173	$P 6_{3}$	1
	63	$C m c m$	2		176	$P 6_{3} / m$	1
	64	$B m a b$	1		180	$P 6_{2} 22$	3
	70	$F d d d$	1		186	$P 6_{3} m c$	12
Tetragonal	82	$I \bar{4}$	1		187	$P \bar{6} m 2$	1
	87	$I 4 / m$	1		189	$P \bar{6} 2 m$	1
	88	$I 4_{1} / a$	6		191	$P 6 / m m m$	12
	92	$P 4_{1} 2_{1} 2$	1		194	$P 6_{3} / m m c$	19
	122	$I \bar{4} 2 d$	2	Cubic	198	$P 2_{1} 3$	1
	123	$P 4 / m m m$	1		204	$I m \bar{3}$	3
	129	$P 4 / n m m$	1		205	$P a \bar{3}$	8
	131	$P 4_{2} / m m c$	1		206	$I a \bar{3}$	3
	136	$P 4_{2} / m n m$	17		216	$F \bar{4} 3 m$	23
	137	$P 4_{2} / n m c$	1		217	$I \bar{4} 3 m$	1
	139	$I 4 / m m m$	3		221	$P m \bar{3} m$	22
	140	$I 4 / m c m$	1		223	$P m \bar{3} n$	2
	141	$I 4_{1} / a m d$	6		224	$P n \bar{3} m$	2
	142	$I 4_{1} / a c d$	1		225	$F m \bar{3} m$	73
					227	$F d \bar{3} m$	12
					229	$I m \bar{3} m$	13
					230	$I a \bar{3} d$	1

The reference set consists of 337 inorganic compounds with 553 symmetry-independent lattice parameters. The experimental lattice parameters were taken from previous benchmark sets listed above, and from measurements at very low temperature or obtained by extrapolation to 0 K. Only the lengths of the unit cell vectors were taken as parameters, because the number of symmetry-independent angles that has been measured at low temperature is too small to allow for statistical evaluations. The measured values were then corrected for zero-point energy effects (ZPEC) via the quasi-harmonic approximation (QHA).¹⁵ The QHA introduces the explicit volume-dependence of phonon frequencies by calculating the Helmholtz Free energy $F (V, T)$ as a function of the lattice volume. The equilibrium volume at a given temperature $V (T)$ is the minimum of $F (V, T)$ with respect to $V$ at constant $T$ . Details of the method are described in Reference 16.

The average thermal correction of the room-temperature lattice parameters to 0 K is about 2.1%. The ZPE correction is comparably small, in average 0.3%. For those compounds that were included in earlier benchmark sets, the ZPE corrections obtained in the present study were comparable.

A variety of standard density functional approximations (DFAs) as implemented in the crystal orbital code CRYSTAL23 (v 1.0.1)^{17, 18} was selected for full optimization of the lattice parameters and atomic coordinates of the reference compounds within the given symmetry restrictions. The selected DFAs range from standard GGA to modern hybrid mGGA functionals, see Table 3.

TABLE 3. Density functional approximations employed in this work.

GGA	Global hybrid	Range-separated hybrid	Meta-GGA	Meta-GGA hybrid
PBE¹⁹	PW1PW^{20, 21}	HSE06²²	SCAN²³	r $^{2}$ SCAN0²⁴
PWGGA²⁵			r $^{2}$ SCAN²⁶	M06²⁷
PBEsol²⁸				MN15²⁹
				revM06³⁰
				B1B95³¹
				PW6B95³²

For all CRYSTAL23 calculations, the recently developed pob-TZVP-rev2 basis sets were employed.^33-35 The QHA calculations were performed with CRYSTAL23 employing the PW1PW functional which was used for previous pob basis set optimizations. The global hybrid functional PW1PW is based on PWGGA and contains 20% Fock exchange in the exchange functional.²¹ In problematic cases r $^{2}$ SCAN or PBE was used for the QHA calculations (see the section problematic compounds in the Supporting Information).

The accuracy of the DFAs was assessed by statistical analysis of the deviations from the ZPEC reference values. In addition the deviation for components of the individual elements was also analyzed. This allowed to identify possible weaknesses in the element-specific pob-TZVP-rev2 basis sets. Finally the overall trends in the deviations from experiment were analyzed and discussed.

2 COMPUTATIONAL DETAILS

All structure optimizations and QHA calculations¹⁵ were performed with the CRYSTAL23 program^{17, 18} using the pob-TZVP-rev2 basis sets.^33-35 The integral tolerances for the Coulomb and exchange series were set to rather strict values, $1 0^{- 9}$ , $1 0^{- 9}$ , $1 0^{- 9}$ , $1 0^{- 18}$ , $1 0^{- 54}$ . Also the Monkhorst-Pack grid density was high by employing shrinking factors of 8, 12 and even 24 for metallic systems. The keyword $ATOMSPIN$ was used to control the atomic magnetization for ferromagnetic or antiferromagnetic systems. The DFAs chosen for assessment of their accuracy are listed in Table 1. The selection consists of GGA, global hybrid, short-range corrected, mGGA and global hybrid mGGA functionals, chosen to represent the rungs 2–4 of the Jacob's ladder,³⁶ and to test some recently developed functionals. For each functional the D3 correction with Becke-Johnson damping^{37, 38} was applied to study the effect of London dispersion interaction on the calculated lattice parameters. The QHA calculations were performed employing seven points and volume changes within $\pm$ 1.0% of the calculated minimum lattice volume. The automated procedure implemented in CRYSTAL calculates the anisotropic thermal expansion of crystals by optimizing the lattice parameters with respect to the purely internal energy $E$ at different volumes.¹⁶ In this way temperature-dependent lattice parameters can also be obtained for less symmetric crystal classes. The recommended values for SCF convergence thresholds were used, $1 0^{- 7}$ a.u. for geometry optimizations and $1 0^{- 10}$ a.u. for phonon calculations.

It has to be mentioned that the present structure optimizations do not explicitly take relativistic corrections into account, which might be relevant for heavy elements. Only scalar-relativistic effect are included via the ECPs. Briki et al. found that relativistic corrections change lattice parameters by up to 0.5%.³⁹

3 RESULTS AND DISCUSSION

3.1 Sol337LC reference set

In Table S1 of the Supporting Information, the experimental lattice parameters measured at room temperature (RT), extrapolated to 0 K assuming linear thermal expansion or directly measured at low temperatures (LT), respectively, and corrected for zero-point energy effects by means of the quasi-harmonic approximation (ZPEC) collected in the Sol337LC reference set are listed.

3.2 Overall statistical evaluation of the DFAs

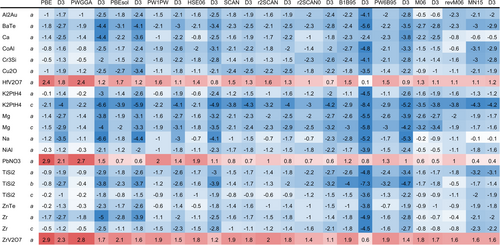
The accuracy of the tested DFAs was evaluated by the mean unsigned relative deviation (MURD), the mean signed relative deviation (MSRD), and the root mean squared relative deviation (RMSRD) of the calculated lattice parameters with respect to the experimental reference data. MURD, MSRD and RMSRD calculated for the Sol337LC reference set are shown in Table 4, ordered from the lowest to the highest MURD.

TABLE 4. Mean unsigned relative deviation (MURD), mean signed relative deviation (MSRD) and root mean squared relative deviation (RMSRD) (%) for ZPEC lattice parameters of the Sol337LC reference set calculated with selected DFAs with and without D3 correction.

DFA	MURD	MSRD	RMSRD
r $^{2}$ SCAN-D3	0.91	−0.20	1.34
SCAN	0.93	−0.09	1.37
SCAN-D3	0.94	−0.31	1.38
r $^{2}$ SCAN	0.95	0.20	1.42
PW1PW-D3	0.97	−0.45	1.37
r $^{2}$ SCAN0	1.04	0.02	1.93
r $^{2}$ SCAN0-D3	1.05	−0.58	1.62
PW1PW	1.06	0.54	1.84
HSE06	1.08	0.53	1.98
PBE-D3	1.14	−0.05	1.60
B1B95	1.21	−0.30	1.83
HSE06-D3	1.25	−0.86	1.77
revM06	1.27	0.31	2.61
MN15-D3	1.31	−0.36	2.29
MN15	1.33	−0.47	2.26
M06	1.37	0.56	2.53
M06-D3	1.41	0.46	2.67
PBEsol	1.41	−0.65	3.39
PWGGA	1.42	0.98	2.05
PBE	1.47	1.06	2.10
PW6B95-D3	1.57	−1.12	2.21
PWGGA-D3	1.60	−0.96	2.31
PW6B95	1.64	−0.07	1.64
PBEsol-D3	1.94	−1.52	3.88
B1B95-D3	3.08	−2.68	4.28

The SCAN family, r $^{2}$ SCAN-D3, SCAN, SCAN-D3 and r $^{2}$ SCAN, provides the highest accuracy. Their MURDs are rather similar, 0.91%–0.95%. For r $^{2}$ SCAN and SCAN, the D3 dispersion correction leads to an underestimation of the ZPEC lattice parameters (MSRDs decrease from 0.2 and $- 0.1$ to $- 0.2$ % and $- 0.3$ %, respectively), but not to significant changes of the MURD and RMSRD. The most accurate hybrid functional among the present selection is PW1PW-D3 (MURD = 1.0%). Also in this case D3 correction slightly improves the MURD, but leads to an underestimation of the ZPEC lattice parameters (MSRD changes from 0.5% to $- 0.5$ %). However, the RMSRD is significantly reduced if dispersion is taken into account, mainly due to the improvements of layer compounds such as graphite and ${MoS}_{2}$ . Unlike PW1PW in comparison with PWGGA, the hybrid functional r $^{2}$ SCAN0 does not represent an improvement over r $^{2}$ SCAN. Without D3 correction the MSRD of r $^{2}$ SCAN0 is almost zero, but MURD and RMSRD are larger than those of the meta-GGA. r $^{2}$ SCAN0-D3 has a similar MURD as r $^{2}$ SCAN0, but tends to underestimate (MSRD = $- 0.6$ %). The frequently used range-separated hybrid functional HSE06 performs similar to PW1PW, however it is not improved by D3 correction. MSRD of HSE06-D3 is strongly negative ( $- 0.9$ % compared to 0.5%), MURD is slightly larger (1.3% compared to 1.1%), and the standard deviation is slightly reduced (RMSRD = 1.8% compared to 2.0%) compared to HSE06.

PBE-D3 is a standard DFA in solid-state quantum chemistry. Its MURD is only slightly larger than those of PW1PW and HSE06 (1.14% compared to 1.08% and 1.06%, respectively). The MSRD is almost zero ( $- 0.05$ %), and the RMSRD is even smaller than those of PW1PW and HSE06 (1.6% compared to 1.8% and 2.0%, respectively). This is in line with the results of previous benchmark tests.⁵ PBE-D3 is therefore an efficient and reliable method for the calculation of solid-state structures. PBEsol, which was specially parameterized for solids, provides only slightly more accurate results compared to PBE (MURD = 1.4% compared to 1.5%, MSRD = $- 0.7$ % compared to 1.1%) However, its RMSRD (3.4%) is significantly larger than for PBE (2.1%). Furthermore, the D3 correction leads to strong underestimation of the ZPEC lattice parameters (MSRD = $- 1.5$ %) and an even larger RMSRD (3.9%), completely different from the original PBE functional. Also the PWGGA functional provides less accurate lattice parameters than PBE (MURD = 1.4%, MSRD = 1.0%, RMSRD = 2.1%). Similar to PBEsol, the accuracy of PWGGA is deteriorated by D3 correction (MURD = 1.6%, MSRD = $- 1.0$ %, RMSRD = 2.3%). In both cases this might be due to the parameterization of the functionals which partially takes into account London dispersion effects. The recently developed hybrid functionals B1B95, revM06, MN15 and PW6B95 are less accurate (MURD ranges from 1.2% to 1.6%, MSRD from $- 0.5$ % to 0.3%, RMSRD from 1.8% to 2.6%). For these functionals, the D3 correction leads to stronger underestimation of the ZPEC lattice parameters. B1B95-D3 shows the largest deviations from experiment of all considered DFAs. revM06 is an improvement over the original version M06 (MURD = 1.3% compared to 1.4%, MSRD = 0.3% compared to 0.6%), although the RMSRD remains almost the same (2.6% compared to 2.5%).

One can argue that the good performance of PW1PW is partially due to the optimization process of the pob-TZVP-rev2 basis sets which was performed with this method. But it has to be mentioned that the pob-TZVP basis sets were also tested for other methods, in particular HF, and also provided improved lattice parameters compared to standard basis sets. We compared the QHA corrections obtained with PW1PW to the PBE corrections that were used in earlier reference sets. Thus the pob-TZVP-rev2 basis sets are intended to be applicable for all DFAs and should lead to improved results compared to standard basis sets.

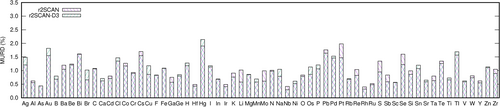
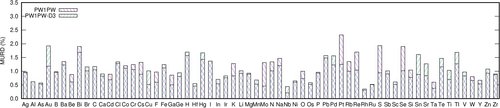
The distribution of the MURD of all compounds of the Sol337LC dataset obtained with the accurate DFAs r $^{2}$ SCAN and PW1PW (with and without D3 correction) is shown in Figure 2. The corresponding MURD distributions of all other DFAs can be found in Figures S1–S5 in the Supporting Information.

Without dispersion correction, the statistics of both functionals shows a large number of overestimations. Both curves have a broad maximum and a shoulder in the positive MURD region. After inclusion of the D3 correction, only maxima are observed at small negative MURD. Overall the D3 correction leads to an improvement of the accuracy for both DFAs, and also to a narrowing of the MURD distribution. However, individual outliers exist which are discussed below.

In general it was observed that the functionals with the lowest MURD also have the smallest standard deviation (RMSRD). However, even the most accurate DFAs have rather high RMSRD, more than 1.3%. Possible reasons for the relatively large discrepancies are the limited quality of particular basis sets, or unreliable experimental reference data. The quality of the atomic basis sets is evaluated by an error statistics of MURD of compounds containing a particular element. A corresponding analysis is provided in Figures 3 and 4 exemplarily for the overall accurate DFAs r $^{2}$ SCAN and PW1PW without and with D3 correction. The element-specific MURD statistics of all DFAs can be found in Figures S6–S18 in the Supporting Information.

For r $^{2}$ SCAN, the largest MURDs are observed for Au, Bi, Hg, Pd and Pt compounds. The D3 correction has a relatively small effect, but slightly increases the mean deviation for Au and Hg compounds, while the results for Pd and Pt compounds are improved. The PW1PW statistics is different from r $^{2}$ SCAN. Here the largest MURD is obtained for Pt compounds, which is however significantly reduced by the D3 correction, and is therefore not a basis set problem. The MURD of Au compounds is only high after D3 correction. In this case the uncorrected PW1PW method gives a reasonable account of the lattice parameters, and the dispersion correction leads to an underestimation, see below. A particularly large MURD is also observed for Bi compounds, for both dispersion corrected and uncorrected PW1PW. Since both functionals show relatively large MURDs for Bi compounds, it is possible that this basis set requires further improvement.

In order to check for the second error source, the inclusion of unreliable experimental reference values, we collect compounds that show over- or underestimation of ZPEC lattice parameters for basically all tested DFAs in Figure 5. The full set of MURD of all tested DFAs is shown in Figures S19–S35 in the Supporting Information.

The experimental references for LT lattice parameters of the elemental metals Ca, Mg, Na, and Zr are assumed to be accurate. The method-consistent underestimation might therefore rather be a consequence of the basis set incompleteness. In our previous works^33-35 we recommended to augment the pob-TZVP-rev2 basis sets by a single diffuse $s$ or $p$ shell for metals. This was also done in the present calculations, but the basis sets apparently require further improvement for metals and intermetallic systems, such as ${Al}_{2} Au$ , BaTe, CoAl, ${Cr}_{3} Si$ , $NiAl$ , and $ZnTe$ . More strikingly is the consistent overestimation of ZPEC LPs for ${HfV}_{2} O_{7}$ , ${PbNO}_{3}$ and ${ZrV}_{2} O_{7}$ . ${ZrV}_{2} O_{7}$ and ${HfV}_{2} O_{7}$ are particular compounds with negative thermal expansion emerging upon structural phase transition at low temperatures.⁴⁰ The experimental low-temperature values for $K_{2} {PtH}_{4}$ are the result of a direct measurement at 9 K.⁴¹ Also this compound is reported to undergo a low-temperature phase transition. These reference data might therefore be taken with some care. The low-temperature LP value of $Pb {({NO}_{3})}_{2}$ was obtained in this work by assuming a linear thermal expansion of the data presented in Reference 42. This is possibly inaccurate in this case, although the same approach was used for many other compounds and did not lead to apparent problems. The accurate calculation of ${TiSi}_{2}$ LPs is problematic for most DFAs, except for r $^{2}$ SCAN and PW1PW without D3 correction. For ${Cu}_{2} O$ an acceptable MURD is obtained with PBE, PW1PW, HSE06, M06 and revM06, while it is problematic for the other DFAs. The observed discrepancies are therefore most probably not due to an inaccurate experimental reference but to the inherent deficiencies of the DFAs.

Further analysis of the performance of PW1PW-D3, HSE06 and r $^{2}$ SCAN for metals and insulators can be found in the SI.

We assess the quality of the pob-TZVP-rev2 basis set by comparing CRYSTAL results to those of the plane-wave method VASP exemplarily for the meta-GGA functional r $^{2}$ SCAN. The plane-wave calculations were performed with VASP (version 6.4.2).^{43, 44} High quality PAW potentials (see POTCARs in SI) were used. A high kinetic energy cutoff of 900 eV was used to approximate the basis set limit. Also FFT grids (Accurate) and SCF thresholds (1.0E $-$ 08 eV) were set to strict values, except for problematic cases. The density of the $Γ$ -centered Monkhorst-Pack integration grids was set to similar values as in the CRYSTAL calculations.

CRYSTAL-r $^{2}$ SCAN and VASP-r $^{2}$ SCAN results were compared to zero-point energy corrected (ZPEC) experimental reference values. For a statistical assessment of the quality of both methods, RMSRD, MSRD and MURD were calculated for the Sol337LC set. The results are collected in Table 5.

TABLE 5. MURD, MSRD and RMSRD (in %) for r

^{2}

SCAN using CRYSTAL and VASP with respect to ZPEC lattice parameters of the Sol337LC set.

Method	MURD	MSRD	RMSRD
CRYSTAL	0.95	0.20	1.42
VASP	0.94	0.69	1.51

The MURD and RMSRD values obtained with CRYSTAL-r $^{2}$ SCAN and VASP-r $^{2}$ SCAN are similar. This underlines the overall quality of the pob-TZVP-rev2 basis sets. However, the MSRD of CRYSTAL-r $^{2}$ SCAN is 0.4%–0.5 % smaller than that of VASP-r $^{2}$ SCAN. This shows that the pob-TZVP-rev2 basis sets tend to underestimate the lattice parameters with respect to the approximate basis set limit, which is an indication for basis set incompleteness. For r $^{2}$ SCAN this leads to a partial compensation of the overestimation of lattice parameters.

4 CONCLUSION

The main purpose of this study was to generate a comprehensive reference benchmark data set for solid-state lattice parameters for comparison with quantum-chemical calculations derived from previous benchmark sets and from experimental lattice parameters at low temperature. For better comparison with the calculations, the low-temperature experimental lattice parameters are ZPE corrected using the QHA. The extended reference benchmark dataset consists of 337 inorganic compounds with 553 symmetry-independent lattice parameters and represents most chemical elements with atomic numbers 1–83 except noble gases and lanthanoids by a minimum of five different compounds. Another purpose of this work was to evaluate the accuracy of selected density functionals. The GGA functionals, PBE, PWGGA and PBEsol, the global hybrid functional PW1PW, the range-separated hybrid functional HSE06, the meta-GGA functionals SCAN and r $^{2}$ SCAN, and the meta-GGA hybrid functionals r $^{2}$ SCAN0, M06, MN15, revM06, B1B95 and PW6B95, all implemented in the crystal-orbital program package CRYSTAL23, were tested. Overall best agreement with experimental ZPEC lattice parameters was obtained with the SCAN functional family and the global hybrid functional PW1PW. The MURD and RMSRD are further improved by the D3 dispersion correction, although it leads to an underestimation of those lattice parameters which were already well described with the uncorrected functionals in some cases. Limitations of the pob-TZVP-rev2 basis sets were analyzed by element-specific calculation of the MURD. The Bi basis set was identified as a possible candidate for further improvement. Experimental low-temperature reference values of ${ZrV}_{2} O_{7}$ , ${HfV}_{2} O_{7}$ and $K_{2} {PtH}_{4}$ cannot be well reproduced with all tested DFAs. These compounds have in common that they are reported to undergo phase transitions at low temperatures. For other compounds such as $Pb {({NO}_{3})}_{2}$ the linear thermal expansion which was assumed in many cases might be problematic. These data might be considered with some care.

ACKNOWLEDGMENTS

The authors thank the High Performance Computing and Analytics Lab of the university of Bonn for computational resources on the bonna cluster and the PC $^{2}$ Paderborn Center for Parallel Computing for providing computer time on the Noctua system. Open Access funding enabled and organized by Projekt DEAL.

Open Research

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions. All CRYSTAL PW1PW inputs are available as Supporting Information to this article.

Supporting Information

REFERENCES

1L. Schimka, J. Harl, G. Kresse, J. Chem. Phys. 2011, 134, 024116.
10.1063/1.3524336
CAS PubMed Web of Science® Google Scholar
2P. Hao, Y. Fang, J. Sun, G. I. Csonka, P. H. T. Philipsen, J. P. Perdew, Phys. Rev. B 2012, 85, 014111.
10.1103/PhysRevB.85.014111
CAS Web of Science® Google Scholar
3J. Wellendorff, K. T. Lundgaard, K. W. Jacobsen, T. Bligaard, J. Chem. Phys. 2014, 140, 144107.
10.1063/1.4870397
CAS PubMed Web of Science® Google Scholar
4P. Pernot, B. Civalleri, D. Presti, A. Savin, J Phys Chem A 2015, 119, 5288.
10.1021/jp509980w
CAS PubMed Web of Science® Google Scholar
5F. Tran, J. Stelzl, P. Blaha, J. Chem. Phys. 2016, 144, 204120.
10.1063/1.4948636
CAS PubMed Web of Science® Google Scholar
6R. Peverati, D. G. Truhlar, J. Chem. Phys. 2012, 136, 134704.
10.1063/1.3698285
CAS PubMed Web of Science® Google Scholar
7T. Gruber, A. Grüneis, Phys. Rev. B 2018, 98, 134108.
10.1103/PhysRevB.98.134108
CAS Web of Science® Google Scholar
8G.-X. Zhang, A. M. Reilly, A. Tkatchenko, M. Scheffler, New J. Phys. 2018, 20, 063020.
10.1088/1367-2630/aac7f0
Web of Science® Google Scholar
9X. Shao, P. Liu, C. Franchini, Y. Xia, J. He, Phys. Rev. B 2023, 108, 024306.
10.1103/PhysRevB.108.024306
CAS Web of Science® Google Scholar
10R. Kingsbury, A. S. Gupta, C. J. Bartel, J. M. Munro, S. Dwaraknath, M. Horton, K. A. Persson, Phys. Rev. Mater. 2022, 6, 013801.
10.1103/PhysRevMaterials.6.013801
CAS Web of Science® Google Scholar
11A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder, APL Mater. 2013, 1, 011002.
10.1063/1.4812323
CAS Web of Science® Google Scholar
12C. Draxl, M. Scheffler, Mat. Res. Bulletin 2018, 43, 676.
10.1557/mrs.2018.208
Google Scholar
13J. E. Saal, S. Kirklin, M. Aykol, B. Meredig, C. Wolverton, J. Mater. 2013, 65, 1501.
CAS Google Scholar
14S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl, C. Wolverton, New Phys. J. Comput. Mater. 2015, 1, 1.
10.1038/npjcompumats.2015.10
Web of Science® Google Scholar
15A. Erba, A. Mahmoud, D. Belmonte, R. Dovesi, J. Chem. Phys. 2014, 140, 124703.
10.1063/1.4869144
CAS PubMed Web of Science® Google Scholar
16R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro, B. Kirtman, Wiley Interdiscip. Rev: Comput. Mol. Sci. 2018, 8, e1360.
10.1002/wcms.1360
Web of Science® Google Scholar
17A. Erba, J. K. Desmarais, S. Casassa, B. Civalleri, L. Donà, I. J. Bush, B. Searle, L. Maschio, L. Edith-Daga, A. Cossard, J. Chem. Theory Comput. 2022, 19, 6891.
10.1021/acs.jctc.2c00958
PubMed Web of Science® Google Scholar
18A. Erba, J. K. Desmarais, S. Casassa, B. Civalleri, L. Dona, I. J. Bush, B. Searle, L. Maschio, L. Edith-Daga, A. Cossard, C. Ribaldone, E. Ascrizzi, N. L. Marana, J.-P. Flament, B. Kirtman, J. Chem. Theory Comput. 2023, 19, 6891.
10.1021/acs.jctc.2c00958
CAS PubMed Web of Science® Google Scholar
19J. P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett. 1996, 77, 3865.
10.1103/PhysRevLett.77.3865
CAS PubMed Web of Science® Google Scholar
20M. Ernzerhof, G. E. Scuseria, J. Chem. Phys. 1999, 110, 5029.
10.1063/1.478401
CAS Web of Science® Google Scholar
21C. Adamo, V. Barone, J Chem Phys 1999, 110, 6158.
10.1063/1.478522
CAS PubMed Web of Science® Google Scholar
22J. G. Brandenburg, E. Caldeweyher, S. Grimme, Phys. Chem. Chem. Phys. 2016, 18, 15519.
10.1039/C6CP01697A
CAS PubMed Web of Science® Google Scholar
23J. Sun, A. Ruzsinszky, J. P. Perdew, Phys. Rev. Lett. 2015, 115, 036402.
10.1103/PhysRevLett.115.036402
CAS PubMed Web of Science® Google Scholar
24M. Bursch, H. Neugebauer, S. Ehlert, S. Grimme, J Chem Phys 2022, 156, 134105.
10.1063/5.0086040
CAS PubMed Web of Science® Google Scholar
25J. P. Perdew, K. Burke, Y. Wang, Phys. Rev. B 1996, 54, 16533.
10.1103/PhysRevB.54.16533
CAS PubMed Web of Science® Google Scholar
26J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew, J. Sun, J Phys Chem Lett 2020, 11, 8208.
10.1021/acs.jpclett.0c02405
CAS PubMed Web of Science® Google Scholar
27Y. Zhao, D. G. Truhlar, Acc. Chem. Res. 2008, 41, 157.
10.1021/ar700111a
CAS PubMed Web of Science® Google Scholar
28J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou, K. Burke, Phys. Rev. Lett. 2008, 100, 136406.
10.1103/PhysRevLett.100.136406
CAS PubMed Web of Science® Google Scholar
29S. Y. Haoyu, X. He, S. L. Li, D. G. Truhlar, Chem. Sci. 2016, 7, 5032.
10.1039/C6SC00705H
PubMed Web of Science® Google Scholar
30Y. Wang, P. Verma, X. Jin, D. G. Truhlar, X. He, Proc Natl Acad Sci 2018, 115, 10257.
10.1073/pnas.1810421115
CAS PubMed Web of Science® Google Scholar
31A. D. Becke, J. Chem. Phys. 1996, 104, 1040.
10.1063/1.470829
CAS Web of Science® Google Scholar
32Y. Zhao, D. G. Truhlar, J Phys Chem A 2005, 109, 5656.
10.1021/jp050536c
CAS PubMed Web of Science® Google Scholar
33D. Vilela Oliveira, J. Laun, M. F. Peintinger, T. Bredow, J. Comput. Chem. 2019, 40, 2364.
10.1002/jcc.26013
CAS PubMed Web of Science® Google Scholar
34J. Laun, T. Bredow, J. Comput. Chem. 2022, 43, 839.
10.1002/jcc.26839
CAS PubMed Web of Science® Google Scholar
35J. Laun, T. Bredow, J. Comput. Chem. 2021, 42, 1064.
10.1002/jcc.26521
CAS PubMed Web of Science® Google Scholar
36J. P. John, K. Schmidt, AIP Conf. Proc. 2001, 577, 1.
10.1063/1.1390175
Google Scholar
37S. Grimme, J. Antony, S. Ehrlich, H. Krieg, J. Chem. Phys. 2010, 132, 154104.
10.1063/1.3382344
CAS PubMed Web of Science® Google Scholar
38S. Grimme, S. Ehrlich, L. Goerigk, J. Comput. Chem. 2011, 32, 1456.
10.1002/jcc.21759
CAS PubMed Web of Science® Google Scholar
39M. Briki, M. Abdelouhab, A. Zaoui, M. Ferhat, Superlattices Microstruct. 2009, 45, 80.
10.1016/j.spmi.2008.12.022
CAS Web of Science® Google Scholar
40Y. Yamamura, A. Horikoshi, S. Yasuzuka, H. Saitoh, K. Saito, Dalton Trans. 2011, 40, 2242.
10.1039/c0dt01087a
CAS PubMed Web of Science® Google Scholar
41W. Bronger, G. Auffermann, Angew Chem Int Ed 1994, 33, 1112.
10.1002/anie.199411121
Web of Science® Google Scholar
42G. K. Bichile, R. G. Kulkarni, Acta Cryst. A 1975, 31, 446.
10.1107/S0567739475001003
Google Scholar
43G. Kresse, J. Furthmüller, Comput. Mater. Sci. 1996, 6, 15.
10.1016/0927-0256(96)00008-0
CAS Web of Science® Google Scholar
44G. Kresse, J. Furthmüller, Phys. Rev. B 1996, 54, 11169.
10.1103/PhysRevB.54.11169
CAS PubMed Web of Science® Google Scholar

Citing Literature

Volume45, Issue32

December 15, 2024

Pages 2702-2709

Extended benchmark set for lattice parameters of inorganic solids

Abstract

1 INTRODUCTION

2 COMPUTATIONAL DETAILS

3 RESULTS AND DISCUSSION

3.1 Sol337LC reference set

3.2 Overall statistical evaluation of the DFAs

4 CONCLUSION

ACKNOWLEDGMENTS

Open Research

DATA AVAILABILITY STATEMENT

Supporting Information

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Extended benchmark set for lattice parameters of inorganic solids

Abstract

1 INTRODUCTION

2 COMPUTATIONAL DETAILS

3 RESULTS AND DISCUSSION

3.1 Sol337LC reference set

3.2 Overall statistical evaluation of the DFAs

4 CONCLUSION

ACKNOWLEDGMENTS

Open Research

DATA AVAILABILITY STATEMENT

Supporting Information

REFERENCES

Citing Literature

Figures

References

Related

Information