RESEARCH ARTICLE

Open Access

Exploring hydrological dynamics of layered pyroclastic soils by combining laboratory and field experiments with a numerical model

Riccardo Busti

Dipartimento di Ingegneria civile, ambientale e meccanica (DICAM), Universita degli Studi di Trento, Trento (TN), Provincia Autonoma di Trento, Italy

Search for more papers by this author

Giovanna Capparelli,

Giovanna Capparelli

orcid.org/0000-0003-3324-8224

Dipartimento di Ingegneria Informatica, Modellistica, Elettronica e Sistemistica (DIMES), Universita della Calabria, Arcavacata di Rende (CS), Calabria, Italy

Search for more papers by this author

Giuseppe Formetta,

Corresponding Author

Giuseppe Formetta

[email protected]

orcid.org/0000-0002-0252-1462

Dipartimento di Ingegneria civile, ambientale e meccanica (DICAM), Universita degli Studi di Trento, Trento (TN), Provincia Autonoma di Trento, Italy

Correspondence

Giuseppe Formetta, Dipartimento di Ingegneria civile, ambientale e meccanica (DICAM), Universita degli Studi di Trento, Via Mesiano 77, Trento (TN), Provincia Autonoma di Trento 38123, Italy.

Email: [email protected]

Search for more papers by this author

Riccardo Busti,

Riccardo Busti

Dipartimento di Ingegneria civile, ambientale e meccanica (DICAM), Universita degli Studi di Trento, Trento (TN), Provincia Autonoma di Trento, Italy

Search for more papers by this author

Giovanna Capparelli,

Giovanna Capparelli

orcid.org/0000-0003-3324-8224

Dipartimento di Ingegneria Informatica, Modellistica, Elettronica e Sistemistica (DIMES), Universita della Calabria, Arcavacata di Rende (CS), Calabria, Italy

Search for more papers by this author

Giuseppe Formetta,

Corresponding Author

Giuseppe Formetta

[email protected]

orcid.org/0000-0002-0252-1462

Dipartimento di Ingegneria civile, ambientale e meccanica (DICAM), Universita degli Studi di Trento, Trento (TN), Provincia Autonoma di Trento, Italy

Correspondence

Giuseppe Formetta, Dipartimento di Ingegneria civile, ambientale e meccanica (DICAM), Universita degli Studi di Trento, Via Mesiano 77, Trento (TN), Provincia Autonoma di Trento 38123, Italy.

Email: [email protected]

Search for more papers by this author

First published: 08 August 2024

https://doi.org/10.1002/hyp.15257

Share a link

Email
Wechat
Bluesky

Abstract

Rainfall infiltration plays a crucial role in the near-surface response of soils, influencing other hydrological processes (such as surface and subsurface runoff, groundwater dynamics), and thus determining hydro-geomorphological risk assessment and the water resources management policies. In this study, we investigate the infiltration processes in pyroclastic soils of the Campania region, Southern Italy, by combining measured in situ data, physical laboratory model observations and a 3D physically based hydrological model. First, we validate the numerical model against the soil pore water pressure and soil moisture measured at several points in a small-scale flume of a layered pyroclastic deposit during an infiltration test. The objective is to (i) understand and reproduce the physical processes involved in infiltration in layered volcanoclastic slope and (ii) evaluate the ability of the model to reproduce the measured data and the observed subsurface flow patterns and saturation mechanism. Second, we setup the model on the real site where soil samples were collected and simulate the 3D hydrological response of the hillslope. The aim is to understand and model the dynamics of hydrological processes captured by the field observations and explain the redistribution of water in different layers during 2 years of precipitation. For both applications, a Monte Carlo analysis has been performed to account for the hydrological parameter uncertainty. Results show the capability of the model to reproduce the observations in both applications, with mean KGE of 0.84 and 0.68 for pressure and soil moisture data in the laboratory, and 0.83 and 0.55 in the real site. Our results are significant not only because they provide insight into understanding and simulating infiltration processes in layered pyroclastic slopes but also because they may provide the basis for improving geohazard assessment systems, which are expected to increase, especially in the context of a warming climate.

1 INTRODUCTION

The soil rainfall infiltration is a physical process of great importance due to its implications for water infiltration, groundwater recharge, surface runoff, subsurface drainage and soil erosion, thus determining the hydro-geomorphological risk level in mountain areas (e.g., Sousa et al., 2020).

Pyroclastic soils refer to alternating layers of volcanic ash, pumice, and other volcanoclastic materials originated from various eruptive phases, that have undergone sedimentation and subsequent physical–chemical alterations (e.g., Basile et al., 2003).

5th May 2023 marked the 25th anniversary of the event occurred in 1998 and considered one of the most catastrophic in terms of economic damage and fatalities (160 deaths) in Italy, when more than 400 landslides affecting shallow pyroclastic deposits in Pizzo d'Alvano (Campania region, southern Italy) were triggered by intense and prolonged rainfall (e.g., Cascini, 2004; Crosta & Dal Negro, 2003; Olivares & Picarelli, 2003).

Rainfall-induced landslides in granular soils are among the most destructive types of natural hazards (e.g., Emberson et al., 2020; Hungr et al., 2001) because of their sudden initiation, high speed of propagation, and increase in mobilized volume during downslope movement (e.g., Damiano et al., 2017; Formetta & Capparelli, 2019; Sorbino et al., 2010), as they can cause damage to buildings, infrastructure and endanger human lives.

This is particularly true for layered pyroclastic soils where the contrasting hydrological properties (e.g., hydraulic conductivity and mechanical features) increase the susceptibility to landslides (e.g., Cascini et al., 2008). The most recent landslide event in Ischia (Gulf of Naples, Campania, southern Italy) occurred during the night between 25th and 26th November 2022, caused 12 victims and destroyed tens of buildings. Therefore, there is a need for improving the physical understanding of the processes that influence the layered pyroclastic soil hydrological response, which in turn will result in improved early warning systems (EWS), saving lives and reduce the societal impact (Costanzo et al., 2015).

Rainfall infiltration process into heterogeneous layered soils represents a complex process, as the contrasting values of hydraulic properties (e.g., saturated hydraulic conductivity) may cause locally diverted flow (e.g., Warrick et al., 1997) or may limit water's infiltration downward from a finer soil into a coarser soil (e.g., Hübner et al., 2017; Stormont & Anderson, 1999). In this context, pyroclastic layered soils differ from traditional homogeneous soils because they originate from volcanic eruptions. During these events, air-fall materials deposit and constitute a sequence of soil layers, which exhibit a high soil porosity and heterogeneous soil structure, permeability and particle sizes (e.g., Picarelli et al., 2006; Roman Quintero et al., 2024).

In the last decades, a great advance in the comprehension of the hydrological processes occurring in the pyroclastic soils focusing on the peri-Vesuvian area, has been achieved through different research techniques, which include (i) long-lasting field monitoring, (ii) laboratory experiments on small-scale physical models and (iii) numerical simulations and (iv) their combination.

Field observations are crucial for collecting long-term hydrological data and developing accurate models of near-surface hydrology of layered pyroclastic soils (e.g., Fusco et al., 2017; Greco et al., 2023). These observations help distinguish between seasonal fluctuations and short-term responses to rainfall. Studies in southern Italy's Cervinara hillslope show that rainfall causes rapid pressure increases near the surface, with less fluctuation in deeper layers (Comegna et al., 2016; Damiano et al., 2012). Seasonal storms in the rainy period December–May can trigger landslides, whereas isolated storms in the period June–August mainly cause erosion (Cascini et al., 2014). One significant feature of pyroclastic soils is the presence of capillary barriers, particularly where coarse pumice layers are interbedded with finer ash layers. These barriers impede vertical water flow, causing water to accumulate above the coarse layers until the hydraulic gradient is sufficient to overcome the barrier (Mancarella et al., 2012; Mancarella & Simeone, 2012). This behaviour was observed over a year of recordings at Pizzo d'Alvano massif (Capparelli & Spolverino, 2022).

Laboratory models of hillslopes allow analysis of hydrological responses under controlled conditions, providing detailed data on pore water pressure, soil moisture and deformations (e.g., Picarelli et al., 2015). Experiments with layered pyroclastic soils show the impact of the pumice layer on flow regimes, delaying wetting fronts and affecting infiltration due to the capillary barrier effect (Capparelli et al., 2020; Damiano et al., 2017; Damiano & Olivares, 2010).

Deterministic hydrological models are powerful numerical tools that simulate interactions between hydrology, geology and geomorphology to understand site responses (e.g., Baum et al., 2010; Cascini et al., 2008; Formetta, Capparelli et al., 2016; Formetta, Simoni et al., 2016; Sorbino et al., 2010). These models, varying in complexity, often use the Richards equation coupled with slope stability models to assess landslide susceptibility. Studies have shown the influence of antecedent conditions on critical rainfall thresholds for landslides, for example, if the dry season is considered, the critical rainfall intensity that triggers landslides remarkably increases (De Vita et al., 2018; Napolitano et al., 2016). Capparelli and Versace (2014) suggest that saturation from deeper layers is not the only reason for instability; rather, the reduction in strength of the upper layer due to water accumulation during prolonged rainfall, combined with short intense storms, leads to hillslope failure. Other studies focused on the influence of topographical factors on landslide susceptibility pointing out critical condition for location where stratigraphic/morphological discontinuities occur, due to localized increase of pore pressure (Cascini et al., 2008; Crosta & Dal Negro, 2003; Tufano et al., 2021). Models are validated against laboratory and field data, showing their reliability in predicting hydrological variables (Damiano et al., 2017; Formetta & Capparelli, 2019; Greco et al., 2013). However, few studies model hydrological variables at both laboratory and hillslope scales (e.g., Damiano & Olivares, 2010).

The aim of this article is to advance the understanding of the hydrological processes occurring in layered pyroclastic soils by exploiting the potential of combining: (i) field measurements, (ii) laboratory experiment results and (iii) model simulations. To reach this goal, we firstly extensively validated and then applied a 3D physically based hydrological model to draw insights on the hydrological infiltration mechanisms occurring in pyroclastic soils. The model applications and conclusions rely on a validation which involves multiple-data (i.e., spatially varying pressure and soil moisture) and multiple-point (across different soil layers and at different depths) measurements, collected across extremely different spatial and temporal scales (from seconds and around one square meter of the laboratory experiments to hourly and half square kilometre of the real site test case).

We focus on two different applications, each of them with specific goals relevance:

Application 1. Objectives: exploiting the measurement data collected in a laboratory test to understand and model patterns and behaviours of pressure and flow fields on a steep, small-scale, layered volcanoclastic slope. Relevance: verify that the numerical model is capable of: (i) reproducing the pressure and soil moisture observations using the data collected in multiple points and depths of the controlled environment and (ii) mimicking the physical processes occurring in the flume during the infiltration test, for example, capillary barrier effect, the temporal variation of the water flux vectors and the water balance.
Application 2. Objectives are: (i) transferring the knowledge gained from Application 1 to the Tuostolo hillslope, where continuous measurements of soil moisture were available for 2 years and (ii) setting up the hydrological model and assess whether it can simulate the hydrological response of such a complex hillslope. Relevance: provide reliable insights on multiple years infiltration processes on a real pyroclastic slope, which in turn will be relevant for assessing landslide susceptible areas, improving the accuracy of EWS.

2 STUDY AREA AND SOIL PROPERTIES

The study area is in Sarno, Campania region, southern Italy. We analyse the Tuostolo hillslope (100–800 m elevation) of the Pizzo d'Alvano massif, where the 5th May 1998, catastrophic landslides occurred (Figure 1a,b). The soil stratigraphy is very heterogeneous in the first few meters below the ground surface along the hillslope cross section (e.g., Cascini et al., 2008). Carbonate rocks are covered by pyroclastic deposits composed of alternating layers of sandy-loam volcanic ash and sandy-gravelly pumice, which are the result of different Somma–Vesuvium eruptive phases and pedogenetic processes (e.g., Capparelli & Versace, 2014; Crosta & Dal Negro, 2003). The hillslope is steep, with angles above 30° and sometimes approaching the measured soil friction angle (38°), where soil stability is achieved through unsaturated pore water pressure (e.g., Capparelli et al., 2020). Rainfall-induced landslides occur in shallow, cohesionless deposits in response to infiltration, which leads to an increase in pore water pressure and thus a decrease in soil strength (e.g., Olivares & Picarelli, 2003).

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

(a) Campania region location in South Italy (the study area is pointed with a black dot); (b) Sarno municipality showing the town, the elevation contours, the 1998 landslides (in red), the analysed Tuostolo site (in blue); (c) flume test sketch showing instrument positions and pressure initial condition. Measures are expressed in (mm); (d) digital elevation model with elevation contour lines every 25 m and monitoring station location, the mapped 1998 landslide is highlighted in red; (e) terrain aspect; (f) surface slope; and (g) soil stratigraphy.

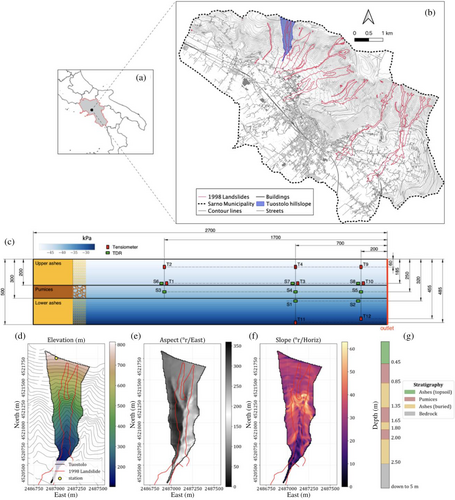
To understand the dynamics of the unsaturated state and the infiltration processes of the soil mantle, a monitoring station consisting of a tensiometer, and five time-domain reflectometers (TDR) was installed in the upper ridge of the Tuostolo hillslope.

3 METHODOLOGY

We use a 3D hydrological model (Section 3.1) to simulate two different applications involving pyroclastic soils, at different spatial and temporal resolutions (Figure 2). First, we reproduce a laboratory experiment to understand the physical processes occurring in a controlled, highly instrumented environment (Application 1, Section 3.2). Afterwards, we move to the application on the real site (Application 2, Section 3.3) to reproduce the hydrological processes at hillslope scale. Model accuracy is assessed in both applications by comparing the time series of measured pressure and soil moisture in different points and at different depths/soil layers. Finally, a Monte Carlo uncertainty analysis is performed to account for the variability of the hydraulic parameters and how this influences the model results (Section 3.4).

3.1 Hydrological model

The GEOtop (i.e., Bertoldi et al., 2006; Endrizzi et al., 2014; Rigon et al., 2006) hydrological model is a computer-based tool used for simulating and analysing each component of the hydrological cycle. It is designed to solve the highly non-linear coupled energy-water balance system at and below the water surface within a watershed using a vertically varying grid and a fixed integration time. The model considers both surface and subsurface components of the hydrological cycle, allowing for a comprehensive understanding of water flow and storage dynamics. The water budget is formulated through the application of the continuity equation at the surface (1.1) to address surface hillslope flow, and the 3D Richards equation (1.2) to resolve the 3D water flux within variably saturated soils:

\left\{\begin{array}{c}\frac{\partial q}{\partial t}+c\nabla \cdotp q=c{q}_{\mathrm{L}}\kern2.75em (1.1)\kern0.5em \\ {}\frac{\partial \theta }{\partial t}+{J}_{\mathrm{w}}=-{S}_{\mathrm{e}}\kern3.75em (1.2)\end{array}\right.,

(1)

where q (L/T) is the runoff discharge per unit of area, c (1/T) is the kinematic wave celerity and

{q}_L

(L/T) is the unit volume flow exchange with soil (i.e., infiltration and exfiltration), θ (−) is the soil moisture,

{J}_{\mathrm{w}}

(L/T) is the unsaturated flow according to Darcy law and

{S}_{\mathrm{e}}

(1/T) is a sink term including the exchange between atmosphere and soil. The hydraulic properties of unsaturated soils follow the Mualem (1976) and Van Genuchten (1980) formulation:

\theta (h)=\left\{\begin{array}{c}{\theta}_{\mathrm{r}}+\frac{\theta_{\mathrm{s}}-{\theta}_{\mathrm{r}}}{{\left(1+{\left|\alpha h\right|}^n\right)}^{1-1/n}},\kern0.5em h<0,n>1\\ {}{\theta}_{\mathrm{s}},\kern0.5em h\ge 0\end{array}\right.,

(2)

\mathrm{k}(S)={k}_{\mathrm{s}}\sqrt{S}\left[1-{\left(1-{S}^{\frac{n}{n-1}}\right)}^{1-1/n}\right],\kern1em S=\frac{\theta -{\theta}_{\mathrm{r}}}{\theta_s-{\theta}_{\mathrm{r}}},

(3)

with

h

(kPa) is the soil pressure,

{\theta}_{\mathrm{r}}

(−) and

{\theta}_{\mathrm{s}}

(−) are the residual and saturated soil moisture,

k

(mm/s) and

{k}_{\mathrm{s}}

(mm/s) are the unsaturated and saturated hydraulic conductivities,

S

(−) is the saturation degree,

\upalpha

(1/kPa) is related to the inverse of the air-entry pressure, n (−) is a measure of the pore-size distribution. Equation (2) is the soil water retention curve (SWRC) and Equation (3) is the hydraulic conductivity function (HCF). The parameters used in our tests are described in Sections 3.2 and 3.3.

The energy balance is computed with respect to volumes where the energy content of the water and soil are considered together:

\frac{\partial U}{\partial t}+\nabla \cdotp g=0,\kern1em g={R}_{\mathrm{n}}+H+\mathrm{LE},

(4)

where U (J/m³) is the internal energy density, g (W/m²) is the sum of the energy fluxes between soil, vegetation and atmosphere (i.e.,

{R}_{\mathrm{n}}

is the net radiation, H is the sensible heat and LE is the latent heat). The net radiation is computed as sum of the net shortwave radiation modelled using Iqbal (1983) formula, and the net longwave radiation modelled using the Stefan–Boltzman equation, where the incoming radiation is function of the atmospheric emissivity computed according to Brutsaert (1975a) (as function of air temperature and water vapour pressure) and the upwelling radiation is based on the surface temperature.

The model can be used in high mountain areas with complex terrain considering environmental and topographic variability (Fiddes et al., 2015; Gubler et al., 2013) to estimate a variety of processes including soil water (Bertoldi et al., 2014) and soil temperature distribution (Bertoldi et al., 2010). The radiation budget includes the shadowing of direct solar radiation by surrounding mountains and the effect of topography on diffuse radiation (Endrizzi et al., 2014). The turbulent fluxes of sensible and latent heat are calculated with the flux–gradient relationship (Brutsaert, 1975b; Garratt, 1992) as function of the surface temperature and specific soil moisture between soil and atmosphere, respectively.

The actual evapotranspiration ET (L/T) is computed as sum of three different components (Rigon et al., 2006):

ET=\left(1-{c}_{\mathrm{f}}\right)E+{E}_{\mathrm{v}}+{c}_{\mathrm{f}}T,

(5)

where

E

is the evaporation from bare soil (Feddes et al., 2001),

{E}_{\mathrm{v}}

is the evaporation from the wet vegetation (Deardorff, 1978),

T

is the transpiration (Best, 1998; Wigmosta et al., 1994), and

{c}_{\mathrm{f}}

is the canopy fraction. The model uses a double layer structure to represent the fluxes from the vegetation to the ground surface and vice versa (Endrizzi & Marsh, 2010).

Model input maps include vegetation cover, soil properties and topography, to capture the spatial heterogeneity of the landscape. Surface parameters related to energy fluxes consist in a single number for each pixel, while subsurface thermodynamic and hydraulic parameters can vary with depth and horizontal extent. Meteorological input data are assigned from weather stations or interpolated from larger-scale climate datasets. Model outputs include time varying maps for each soil layer of pore pressure and soil moisture, and maps of water table depth, actual evapotranspiration and surface water. In addition to that, the model can print the time series of pore pressure, soil moisture, temperature for selected points and the discharge at the hillslope outlet.

3.2 Application 1

The first application aims to simulate a physical model of the typical Sarno slope (Figure 1c) built in the experimental flume test presented in Capparelli et al. (2020) (Figure S1). Soil samples from buried ashes and pumices (Figure 1g) were collected to build the layered flume. The small-scale slope is a 38° layered deposit composed of three soil layers: a 10-cm-thick pumice soil is interbedded between two 20-cm-thick layers of volcanic ash (total depth is 50 cm). The deposit is 270 cm long and 60 cm wide. The initial condition is a dry soil profile with a near hydrostatic pressure distribution. Water can drain out the system downslope with both surface and subsurface flow mechanisms through a perforated panel with gutters. On the other sides (lateral and bottom), the model is confined to achieve impermeable boundaries. The infiltration test consists of a sprinkling experiment with piecewise constant rainfall intensity (R) varying on time:

R(t)=\left\{\begin{array}{c}32\ \mathrm{mm}/\mathrm{h}\kern1.50em 0\le t\le 151\ \min \\ {}9\ \mathrm{mm}/\mathrm{h}\kern1.25em 151<t\le 257\ \min \\ {}0\ \mathrm{mm}/\mathrm{h}\kern1em t>257\ \min \end{array}\right..

The system is highly instrumented: a high density of small instruments (eight tensiometers and eight TDRs) collected the measurements in time of the main physical quantities (pressure and soil moisture) amidst all soil layers and along the critical areas such as at the surface, the interfaces, the bottom and near the outlet (Figure 1c). Two rows of tensiometers are positioned in the upper ash layer: a first series of three tensiometers (T9, T4 and T2) is located 6 cm below the topsoil surface to catch the shallowest layers response, and the second series of three instruments (T10, T3 and T1) is placed at a depth of 18.5 cm directly above the upper ash–pumice interface, each from downstream to upstream. In addition, three TDRs (S8, S7 and S6) are positioned in the same location as the latter tensiometers. In the pumice plane, three TDRs (S5, S4 and S3) are in the middle of the soil at a depth of 25 cm. At the bottom of the small-scale model, one tensiometer (T12) is placed downstream at a depth of 45.5 cm, while the other (T11) is in the middle of the channel at a depth of 48.5 cm. We set up the GEOtop model using a digital elevation model (DEM) with horizontal resolution of 50 mm and vertical grid resolution of 20 mm. A no-flux boundary condition is applied to all lateral sides and at the bottom, except for the downstream outlet where the water can flow out of the system.

Hydraulic parameters mentioned above (Equation 1) were estimated by fitting the SWRC using tensiometers and TDR measurements. Upper and lower ash parameters are assumed to be the same since they are constructed from the same soil material (Capparelli et al., 2020). The saturated hydraulic conductivity for the ashes is assigned following the experiment results described in Sorbino and Foresta (2002) and Bilotta et al. (2005), where it was estimated in laboratory by performing suction controlled oedometer tests on the undisturbed Tuostolo specimens. For the pumice layer, we apply the hydraulic parameters set provided in De Vita et al. (2013) (Section 3.3). The parameters are detailed in Table 1, with the corresponding SWRC and HCF sketched in Figure S2.

TABLE 1. Hydraulic parameters used.

	${k}_{\mathrm{s}}$ (mm/h)	${\theta}_{\mathrm{r}}$ (−)	${\theta}_{\mathrm{s}}$ (−)	$\alpha$ (1/kPa)	$n$ (−)
Lab
Ashes (upper and lower)	72	0	0.4	0.26	1.29
Pumices	36 000	0	0.56	4.2	1.43
Real site
Ashes (topsoil)	1800	0	0.4	0.36	1.42
Pumices	36 000	0	0.56	4.2	1.42
Ashes (buried)	36	0	0.37	0.17	1.4
Bedrock	3	0	0.6	0.37	2

3.3 Application 2

In this application, the GEOtop model is set up on the Tuostolo hillslope (Figure 1d–f). The hillslope, spanning 0.35 km², exhibits a north-west aspect orientation and an elevation range from 110 to 814 m. Characterized by slopes averaging between 30° and 38°, with a maximum slope of 62° at 470 m elevation, the area is covered by deciduous forest vegetation. The stratigraphy used in the model is presented in Figure 1g. Following Capparelli and Spolverino (2022), we consider an alternating scheme ash–pumice soil layers with progressive depths of 0.45, 0.85, 1.35, 1.65, 1.80, 2.00 and 2.50 m from the surface. The vertical discretization is 50 mm, while the horizontal one corresponds to the available DEM spatial resolution (7 m). No flow lateral boundary conditions are assumed, and water can flow out from the downstream outlet of the reach. A free drainage lower boundary condition is set at the bottom of the 5 m bedrock thickness, as in Napolitano et al. (2016). We used a 3 m water table depth as the initial condition (consistent with other studies, e.g., Tufano et al., 2021) and we use a 3-month period for model spin-up. The model is executed from 1 October 2007 to 1 October 2009, during which data of precipitation and air temperature have been recorded at hourly time step. The mean precipitation rate is 0.17 mm/h and the highest recorded precipitation peak of 21.4 mm/h occurred at 11:00 PM on 3 January 2009; the cumulative observed precipitation is 2548 mm. The modelled pressure and soil moisture time series are compared with the available observations: one tensiometer located in the topsoil at 0.3 m depth and six TDRs, three located in the topsoil (at 0.1, 0.2 and 0.3 m depth), two located in the pumice layer (at 0.6 and 0.7 m depth), and one located in the buried ashes (at 0.9 m depth). The SWRC parameters for the ashes (topsoil and buried) were estimated by fitting the SWRC using tensiometers and TDR measurements in the respective layers. The saturated hydraulic conductivity for the ashes (topsoil) is assigned based on the field data analysis presented in Capparelli et al. (2022). The parameters for the ashes (buried) and pumices are assigned according to the experiments described by De Vita et al. (2013) who analysed soils samples in the same study area. Saturated hydraulic conductivities for both layers were estimated through Compact Constant Head Permeameters, while the pumice SWRC parameters were determined using “Temple Cell” equipment. The parameters are detailed in Table 1, with the corresponding SWRC and HCF sketched in Figure S2. For the bedrock layer, we prescribed the Van Genuchten parameters as presented in Capparelli and Versace (2014).

3.4 Model performances quantification and uncertainty analysis

The Kling–Gupta efficiency coefficient (KGE, Gupta et al., 2009) is used to quantify the model performance in simulating the spatial and temporal pressure and soil moisture trends in different soil layers. KGE provides a diagnostically interesting decomposition of the Nash–Sutcliffe efficiency, which facilitates the analysis of the relative importance of its different components, namely correlation (r), bias (b) and ratio of variances (a) between measured (M) and simulated (S) values:

\mathrm{KGE}=1-\sqrt{{\left(r-1\right)}^2+{\left(a-1\right)}^2+{\left(b-1\right)}^2},

(6)

r=\frac{\mathrm{co}{\mathrm{v}}_{M,S}}{\sigma_S\cdotp {\sigma}_M},\kern1em a=\frac{\sigma_S}{\sigma_{\mathrm{M}}},\kern1em b=\frac{\mu_S}{\mu_M},

where

\operatorname{cov}

denotes the covariance,

\sigma

is the standard deviation and

\mu

is the arithmetic mean. KGE values range from (−∞ to 1]: negative and small values indicate poor correlation, 1 indicates perfect correlation.

To evaluate the uncertainty of the hydraulic parameters (Table 1), we perform a Monte Carlo simulation analysis based on 500 parameter sets drawn from a lognormal distribution (e.g., Formetta, Capparelli et al., 2016; Formetta, Simoni et al., 2016; Smith & Hebbert, 1979). Accordingly, we assumed θr, θs, ks, α and n, as random variables with standard deviation equal to a 10% of the mean values (Table 1), for both ashes and pumices, consistently with other studies which used the same method (e.g., Arnone et al., 2016). In this way, we account for the possible uncertainty in the hydrological parameter's estimation.

4 RESULTS

4.1 Application 1

The model is capable to mimic the evolution of pressure and soil moisture (specifically time of rise and peak values) at all monitored points (Figure 3), with a mean KGE of 0.84 for the tensiometers and 0.68 for the TDRs. Bold curves in Figure 3 correspond to the simulation performed with the parameters listed in Table 1, while the shaded coloured area is the 95% prediction interval based on the Monte Carlo analysis. The discrepancy between the pressure and soil moisture KGEs can be partially explained by two main reasons. From the model's perspective, uncertainties arise from the SWRC parameters, which may exhibit local differences compared to the undisturbed specimens from which they were estimated, and from the numerical scheme adopted to solve the water balance and handle the hydraulic conductivity at the interface between two highly contrasting soil textures. From the data perspective by the different measurement techniques used for tensiometers and TRDs: while the former measure soil pressure directly at the porous ceramic cap, the latter measure soil moisture in the surrounding soil in an implicit way (e.g., Spolverino et al., 2019) based on measuring the electromagnetic wave time over the probe, which depends on the dielectric constant calculated as a function of the average soil moisture along the device. Thus, unless the instrument is sufficiently small, the TDR readings may also be affected by higher uncertainty, especially at contrasting soil layer interfaces. The tensiometers placed at 6 cm depth (i.e., T2, T4 and T9) in the upper ashes show an immediate increase in pressure after 15 min from the start of the rainfall. The pressure increases from the extremely dry initial condition of −50 kPa to approximately −10 kPa in the first 30 min of the experiment. In the following hours, the pressure continues to rise to nearly 0 kPa without reaching full saturation at the end of the highest rainfall intensity. During the low intensity rainfall, the pressure sets around −2 kPa after an initial small decrease. At the end of the experiment, both simulated and observed curves show similar pressure values and a slight drainage (decrease in pressure) when rainfall is stopped. The tensiometers located at 18.5 cm depth (i.e., T1, T3 and T10), above the upper ash–pumice interface, show a nearly perfect overlap between measured and simulated values with a mean KGE of 0.90. The pressure dynamics is well captured by the model, with the tensiometer T1 rising being slightly delayed in the first phase of the experiment (32 mm/h rainfall intensity). Pressure rises from initial dry state of −45 kPa, to a wet state close to saturation. During low rainfall intensity, these tensiometers show the same behaviour as the previous set. Last, in the lower ash tensiometers (i.e., T11 and T12), the simulated pressure increases after 4 h, consistently with the records, from −30 to −10 kPa, with an underestimation for the tensiometer in the centre of the flume and at the outlet (i.e., T11 and T12).

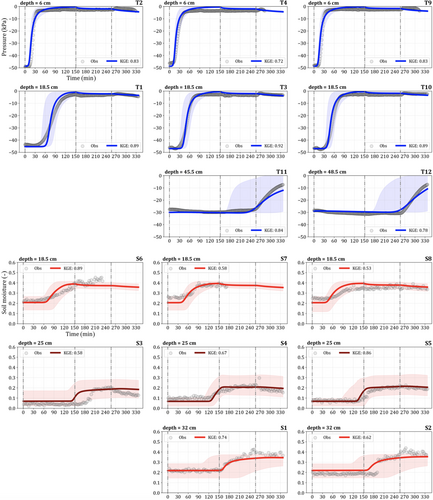
The shallowest TDRs (i.e., S6, S7 and S8) response follows that of the tensiometers placed in the same position: we observe an increase in soil moisture at the upper interface in correspondence of the rising pressure after 60 min in T1 and 30 min in T3 and T10. The model predicts an initial drier condition of 0.20, which is more evident in S7 and S8, with respect to the observed soil moisture around 0.25. The soil moisture in the topsoil nearly reaches the saturation value θs = 0.40 at the end of the 32 mm/h intensity rainfall. The modelled soil moisture levels in the pumice layer (i.e., S3, S4 and S5) reproduce the observed pattern, with one exception for the initial condition of the last two instruments and an anticipated rising for S3. The initial soil moisture is near the residual soil moisture θr = 0, and the wetting phase begins around 125 min until the coarse layer reaches a peak value of 0.20, far below the soil moisture at saturation θs = 0.56, implying that water is either stored in the finer upper layer or flows into the bottom layer. In the deepest TDRs (i.e., S1 and S2), the pattern is well captured for the first one, and for the second one, the increase in soil moisture exhibits a time discrepancy of 30 min when compared with observations. Additionally, the model predicts lower soil moisture values (0.35) at the end of sprinkling experiment compared with the data.

The pore water pressure prediction interval (Figure 3) is restrained to around $\pm$ 5 kPa in magnitude and few minutes in time when considering the tensiometer at 6 cm depth (i.e., T2, T4 and T9) and to around $\pm$ 10 kPa and few minutes for the tensiometer close to the interface (i.e., T3 and T10), with the exception of T1 for which the error can be larger (up to $\pm$ 20 kPa and 30 min). Conversely, when we consider the bottom tensiometers (i.e., T11 and T12), the error can be quite large: the pressure rising in the lower ashes can be either anticipated or delayed by over 1 h. The uncertainty in the TDR measurements is evident in both the timing and magnitude of soil moisture (±0.10) across all layers. Deeper devices experience more significant errors, leading to a 30 min anticipation or delay and an overestimation of soil moisture (θ > 0.30) in the pumice layer, as well as a 60 min delay in the lower ashes.

The objective of this first application was not only to replicate the laboratory observations but also to verify that the model can reproduce the infiltration processes regarding subsurface water flow in the volcanoclastic layered deposit. Figure 4a shows the orientation of the normalized flux vectors (with respect to the flux magnitude) and the pressure evolution with the propagation of the wetting front at different time steps for a cross section located at the centre of the flume. At the beginning of the experiment, the fluxes are slope normal in correspondence with the wetting front, as seen in Lu et al., 2011 for a homogeneous slope: the main contribution to the water flow direction is capillary. After 2 h, the wetting front reaches the first interface. The pressure in the topsoil is constant and the vectors are moving from a normal to a vertical direction thanks to the increasing effect of the gravity. After 3 h, the wetting front arrives at the bottom of the pumice layer. The accumulation of water at the interface is responsible for the rise of the water level in the upper ash, however, saturation is not reached. The fluxes are gaining a non-negligible horizontal component, which is more evident close to the first interface due to a redirection of flow downstream in the channel. After 4 h, infiltration process also develops in the lowest layer (orthogonal fluxes). After 5 h, the water level decreases in the upper ashes and the flux orientation are almost slope parallel, while in the pumice and lower ashes, infiltration is still ongoing. At the last time step, after 6 h, the flux directions in the topsoil are slope parallel, that is, the soil is draining, while the accumulated water in the lower ashes is flowing downslope along the impermeable bottom.

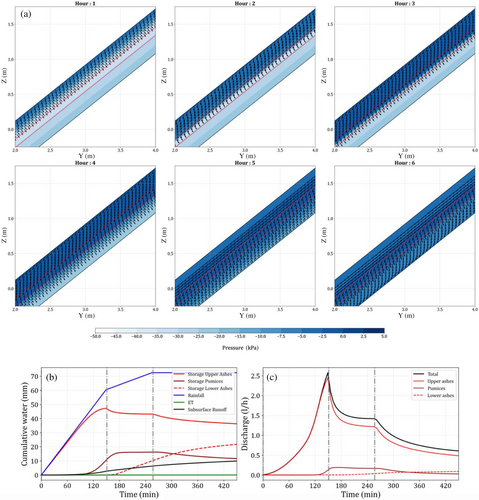
Figure 4b illustrates the water balance for the flume test in terms of the specific cumulated volume from the start of the experiment. Most of the infiltration water is retained in the first layer of the soil during the initial phase of the experiment, reaching a maximum level of 47 mm at the end of the high-intensity rainfall. Subsequently, storage in the pumices begins to increase after 90 min. During low-intensity rainfall, the storage in the upper ashes layer gradually decreases to 43 mm due to lateral runoff and infiltration towards the pumice layer itself, reaching a plateau of 16 mm. Only after 3 h from the beginning of the experiment, the storage in the lower ashes starts to increase reaching a maximum of 22 mm. The evaporation from the bare soil surface constitutes only a small fraction of the water balance.

The cumulated lateral subsurface runoff, computed at the downstream face of the flume, considers contributions from all soil layers (Figure 4c). The upper ashes make the most significant contribution to subsurface runoff. The peak discharge of 2.5 L/h in the uppermost soil is observed at the end of the high-intensity rainfall, decreasing up to 1.44 L/h in the second phase and further diminishing in the last drainage phase when rainfall ceases. The pumice contributes only 12% to the subsurface water flow, with a maximum computed discharge of 0.19 L/h after 150 min. Runoff from the lower ashes develops at the base of the flume only after water begins to flow along the bottom.

4.2 Application 2

Figure 5 shows the comparison between observed and modelled time series of the hydrological variables of the real site. The model mimics the pressure observed by the tensiometer at 0.3 m depth (i.e., TENSIO3) quite well, with a KGE of 0.83. During the rainy season, pressure values are consistently negative, around −10 kPa, with fluctuations in accordance with storm peaks. During the dry season, pressure decreases to its lowest values. Owing to the absence of precipitation and the prevailing evapotranspiration, the soil becomes dry (pressure ∼ −50 kPa). We overestimate pressure values in late May–June 2008 and 2009 during dry weeks with no precipitation events. The topmost TDR, named TDR1, is located at a depth of 0.1 m in the upper ashes. The soil moisture dynamics is consistent with the observed trend in both simulated years. During summer, we observe a constant decrease in soil moisture, implying that the topsoil is draining and evaporating; in contrast, in fall, winter, and spring, soil moisture fluctuations appear in correspondence of the rainstorm events. The topsoil never reaches saturation: the maximum soil moisture values of ∼0.3 are below the saturated soil moisture of 0.4. TDR2 and TDR3 show similar behaviour as the previous one, with the same pattern but slightly lower peak values. At these depths, agreement with observations is higher, even for the drier periods, with an overall KGE of 0.80 for the first probe and 0.71 for the second one. TDR6 and TDR7 give an insight into the upper pumice layer. The average soil moisture of 0.07 is far below the saturation value of 0.56, that is, the pumice layer remains very dry during the simulation. The fluctuations in the coarse layer are less pronounced than in the upper finer layer. In December 2008–January 2009, the model simulates two peaks around 0.2, but even in this case, the soil is only 33% saturated. In general, the pumice layer is less saturated than the ashy topsoil, meaning that most of the water percolating in the soil is stored in the top layer or drains to the deeper horizons. The temporal pattern is well captured by the model, but during storms, it simulates slightly higher peaks in correspondence of more flat records. The TDR placed in the lower ashes (i.e., TDR9) at 0.9 m depth exhibits small changes in soil moisture values around 0.25. During the wet season, the model predicts fluctuations during the most intense storms, differently from the uppermost devices (TDR1, TDR2 and TDR3) where the response to precipitation events is quicker and pronounced. During the wet season, we do not observe significant fluctuations in the buried ashes as compared to the upper ashes. At greater depths, the behaviour of the finer soil is likely to be influenced by a seasonal trend rather than a single rainstorm.

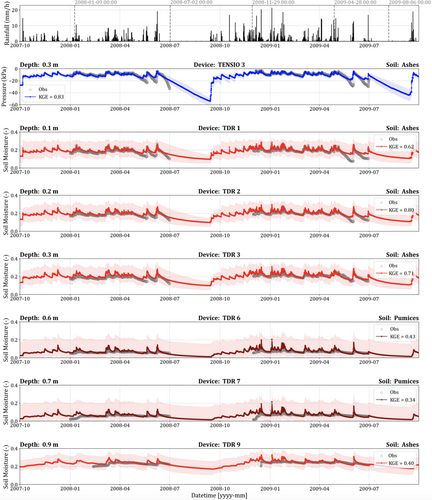
The pressure prediction interval in Figure 5 is wider during the dry season in the descending phase when the pressure decreases, while the TDR one shows a consistent overestimation (underestimation) of the soil moisture during all the years in all layers. Small changes in the SWRC parameter values can either increase (decrease) the soil moisture by over 50%. As observed in the first application, larger differences in the model outputs occur in the deeper layers.

Figure 6 displays the pressure maps above each soil interface at the five different time steps annotated in Figure 5. The first row shows the pressure layers on 9th January 2008. At this time, a vertical and horizontal difference in pressure distribution is remarkable: rainfall from the previous months accumulated in the middle layers and especially along the concave areas. In contrast, the topsoil shows an almost uniform pressure distribution along the hillslope, determined by the precipitation of the day. During the summer (2nd July 2008), the uppermost and deepest layers show lower values of pressure in contrast to the middle layers. Most of the water is stored in the intervening horizons, while the uppermost soil hydrological processes are dominated by evapotranspiration. During the prolonged storms of 29th November 2008, the hillslope shows a uniform pressure distribution both along the profile and in the plain. The predicted pressure reaches its highest values between −5 and −2.5 kPa, but no positive values are observed. In spring, on 28th April 2009, the pressure field at different depths is similar to that observed January: in the upper layers, the waterfront infiltrates and the water is stored in concave areas and channels, while in the deeper layers, the water flows downhill or infiltrates towards the bedrock. The last time level, dated 6th August 2009, shows the most critical situation in terms of water stress during the summer due to the prolonged dry period.

Figure S3 shows the daily actual evapotranspiration flux. Results show the typical seasonal trend with the maximum evapotranspirated water of around 4 mm/day during the summer and the minimum during the winter.

5 DISCUSSION

5.1 Hydrological response of layered pyroclastic soils

The two applications provide in-depth insights into hydrological processes in unsaturated layered pyroclastic soils, emphasizing the importance of considering multiple scales and multi-data point measurements for a comprehensive understanding.

Previous research by Olivares and Damiano (2007), Damiano and Olivares (2010) and Spolverino et al. (2019) conducted flume tests on homogeneous fine ash slopes during transient rainfall, revealing the presence of a water table at the bottom. In contrast, studies by Damiano and Olivares (2010), Damiano et al. (2017) and Damiano (2019) investigated small-scale layered slopes with a layer of coarse pumice between two fine ash soils. In our study, we build upon this work by extending the model validation/assessment to include measured soil moisture time-series across all soil layers, with a specific focus on the intervening pumice layer's role in regulating water storage, infiltration dynamics and soil response to precipitation across different spatial and temporal scales.

Pumices, characterized by high porosity and permeability, exert significant capillary forces due to their irregular surface structure and interconnected pore spaces. When dry, these pumice layers hinder water infiltration into underlying layers (e.g., Capparelli & Spolverino, 2022; Mancarella et al., 2012; Mancarella & Simeone, 2012), resulting in water accumulation within the finer ash layer above, affecting soil cover stability and promoting lateral flow along the upper interface. Despite the pumice layer exhibiting a saturated hydraulic conductivity two orders of magnitude higher than ash layers, the wetting front progression within pumices is slower compared to ashes (Figures 3 and 4). This phenomenon can be explained through hydraulic conductivity curves, indicating that at pressure values near saturation, pumice demonstrates greater unsaturated hydraulic conductivity than ashes. However, once a specific pressure threshold is reached (−2.5 kPa), ash conductivity surpasses that of pumices by orders of magnitude (Figure S2b). Once a sufficiently high gradient is established across the interface, the vertical water flow proceeds to deeper depths. This situation depends on two factors: the initial soil moisture condition and the duration/intensity of the storm.

A sensitivity analysis using GEOtop was conducted to assess the impact of variable duration-intensity rainfalls, revealing distinct responses. We considered two opposite scenarios: (i) a high intensity/short duration rainfall, that is, 100 mm/h lasting for 30 min, and (ii) a medium–low intensity/long duration rainfall, that is, 30 mm/h lasting for 5 h. Results are presented in Figure S4. During the first test (Figure S4a,b), the dry pumices confine the infiltrated water to the upper ashes, resulting in subsurface parallel flow along the upper interface due to the established enhanced slope parallel hydraulic gradient. After the event, once the capillary barrier is breached, water begins to infiltrate into the pumice layer. In contrast, for the second rainfall test (Figure S4c,d), the infiltrated water can reach the deeper layers. The water accumulated in the pumices and lower ashes significantly contributes to the total discharge. The storage in the bottom layer is high and comparable with that in the first layer. In this scenario, the uniform pressure condition along the soil depth and the potential development of a water table at the base of the flume are likely responsible for the instability of the entire flume.

In the real site application, the prolonged dry or wet periods influence the initial conditions from which the short-term response of the soil cover evolves during individual events (e.g., Comegna et al., 2016; Fusco et al., 2017). During a rainstorm at the beginning of the rainy season (September–October), when the soil profile is dry, the intervening pumice capillary barrier effect prevents infiltration from penetrating deeper layers, resulting in water accumulation and lateral flow in the upper layers. In this case, the cause of the landslide trigger mechanism is the reduction of strength in the shallowest layers as highlighted by Capparelli and Versace (2014). During winter and spring seasons (November–June), when the pressure profile is very smooth and close to saturation due to the frequent rainstorms, the barrier established by the pumices disappears and infiltration prevails over lateral flow. Therefore, rain-triggered landslides in Campanian pyroclastic soils occur mainly at the end of winter or early spring (i.e., Sarno 5th May 1998, Cervinara 15th December 1999), when the soil profile is wet and close to saturation (Figure 6; November–April). The arid hydrological condition prevailing at the end of summer strongly inhibits slope instability under most precipitation conditions (e.g., Napolitano et al., 2016).

Another factor influencing slope instability is the site morphology. The 3-D GEOtop hydrological model allows treatment of complex surface and bedrock topographies, with a particular focus on convergent sites where headwaters are formed by the accumulation of groundwater (subsurface flow and seepage) and surface water in channels, or divergent sites where water flow spreads. Water can accumulate in colluvial depressions, raising the water table and increasing pressure head (Figure 6; buried layers). This intricate interaction of terrain features and water distribution across multiple dimensions can significantly impact the stability of slopes, especially in scenarios involving multiple soil layers, as more layers are involved in the stability dynamics than in planar or simpler morphologies. (e.g., Formetta & Capparelli, 2019; Formetta, Capparelli et al., 2016; Formetta, Simoni et al., 2016).

Consistently with the approach used in previous studies (e.g., Arnone et al., 2016; Dai & Lee, 2002; Formetta, Capparelli et al., 2016; Formetta, Simoni et al., 2016), we explored the influence of model parameters uncertainty on hydrological predictions by describing their distributions using mean values and standard deviations, computed as percentage of the mean. Results show that in some cases, model predictions highly depend on these values, and therefore, proper quantification of parameters, such as mean values and standard deviation, is crucial. In particular cases (i.e., for the pumices and bottom ashes in Figures 3 and 5), accounting for a variance of only 10% of the mean parameter values may result in very spread model predictions. For our test site, this can be partially attributed to (i) the non-linearity of the SWRC and (ii) the stratified setting of soil layers, which control the retention behaviour and the temporal delay in the wetting front propagation.

5.2 Limitations

For the Application 1, the monitoring network allows an exhaustive comprehension of the hydrological response to rainfall infiltration on the layered slope, being the tensiometers and TDRs buried at different depths in different positions along the slope. However, no tensiometers were installed in the pumices because of technical issues in measuring soil water pressure. As pointed out in Capparelli and Spolverino (2020), it was not possible to establish the necessary hydraulic contact between the coarse gravelled soil and the tensiometer cap. This results as a limiting factor to understand the pressure evolution occurring in the pumice layer.

For the Application 2, only one monitoring station was active near the ridge of the Tuostolo hillslope and has been used to verify the hydrological model accuracy. Although 2 years' worth of hourly records of pore water pressure and soil moisture at various depths are present, the inclusion of additional monitoring stations across the hillslope could have improved understanding of hydrological processes at the hillslope scale, beyond assessing the robustness of the numerical model. Furthermore, the hypothesis used in the model of parallel layers with different soil properties for the entire analysed hillslope could be relaxed if spatial measurements of soil layer thicknesses were available in multiple points. Despite this limitation, the topographic gradient is shown playing a major role in water accumulation ad subsurface flow redistribution.

Due to the lack of subsurface flux measurements in the laboratory application, discharge records at the actual site, and evapotranspiration data, predicting the water balance becomes challenging. To address this, we conducted simulations of various rainfall scenarios to understand potential responses of all the pyroclastic layers in terms of water storage dynamics and subsurface runoff generation.

6 CONCLUSIONS

In this study, we reproduced the hydrological behaviour of layered pyroclastic soils through numerical simulations. Differently from previous studies, we validated a 3D hydrological model using both pressure and soil moisture measurements in multiple locations and depths for two applications, highly different for spatial and temporal scales.

In the first application, we simulated a laboratory physical model of a steep layered slope made of soil samples recovered from the Tuostolo site. In the second test, we simulated the real hillslope during 2 years of recorded precipitation. In both applications, a congruence with measured data was found for all instruments and all hydrological variables.

The Tuostolo hillslope results show that it is possible extend the modelling analysis at nearby non-instrumented sites, where (i) the assumption of similar stratigraphy and composition of the volcanic material is valid or (ii) at site estimations of soil parameters are available. The modelling framework allowed not only to make predictions of soil moisture and pressure values but also to account for model parameters uncertainty through Monte Carlo simulations.

In the flume test, we demonstrated the physical role of the intervening coarse layer: dry pumice initially impedes infiltration, inducing a lateral flow diversion and accumulating water in the upper ash. Once a sufficiently high hydraulic gradient is established across the upper interface, the wetting front can propagate to deeper depths. This effect depends on the intensity and duration of applied rainfall. Flow pattern was reconstructed by analysing the flux vectors high temporal resolution all over the domain. In the real site test, we demonstrated the ability to simulate the observed seasonal variations in pressure and soil moisture response over extended rainfall periods and individual storms across multiple locations, including both shallow and deep depths, despite the presence of contrasting soil layers.

Pressure dynamic in the uppermost layer depends on individual storms, while the response in the deepest layers is less pronounced and depends on the antecedent weekly-monthly precipitation history. The spatial distribution of pressure is heavily influenced by hillslope topography, that is, water accumulates in hollows that are susceptible to landslide events during winter and spring, when soil is wetter and uniform pressure profile develops along the soil depth. This has been presented showing dynamic in time 3D evolution of the pressure field over the hillslope.

The importance of this research lies not only in numerically simulating soil water flow dynamics through pyroclastic soils but also in transferring the concepts learned from small scale to large scale within a consistent, adaptable and physically based framework. This can be useful for further understanding complex hydrological processes and natural hazard assessments like EWS for landslides. For example, result of such 3D water flow models could be combined with geophysical models to evaluate hillslope mechanical stability.

ACKNOWLEDGEMENTS

We thank Doctor Eng. G. Spolverino for sharing all the hydrological records. Giuseppe Formetta is partially supported by the PRINN COACH-WAT (CODE 2022FXJ3NN CUP E53D23004390001). Open access publishing facilitated by Universita degli Studi di Trento, as part of the Wiley - CRUI-CARE agreement.

Open Research

DATA AVAILABILITY STATEMENT

The software used in this paper is open-source and available at https://github.com/geotopmodel/geotop. The simulation results are available for both cases studied on Zenodo at https://zenodo.org/record/8424961 or upon reasonable request to the corresponding author.

Supporting Information

Filename	Description
hyp15257-sup-0001-FigA1.tiffTIFF image, 11.3 MB	Figure S1. Laboratory physical model (a) view from above, (b) lateral view showing the layered soil (detail), (c) downstream outlet gutters (from Capparelli et al., 2020).
hyp15257-sup-0002-FigA2.tiffTIFF image, 14.1 MB	Figure S2. (a) Soil water retention curves and (b) hydraulic conductivity curves for ashes (topsoil and buried layers) and pumices.
hyp15257-sup-0003-FigA3.tiffTIFF image, 6.7 MB	Figure S3. Application 2 results. Daily actual evapotranspiration.
hyp15257-sup-0004-FigA4.tiffTIFF image, 17.5 MB	Figure S4. Application 1 results. (a) Water balance and (b) lateral subsurface runoff redistribution for high intensity/short duration rainfall; (c) water balance and (d) lateral subsurface runoff redistribution for medium–low intensity/long duration rainfall. The dashed vertical lines represent the moments when applied rainfall stops.

Please note: The publisher is not responsible for the content or functionality of any supporting information supplied by the authors. Any queries (other than missing content) should be directed to the corresponding author for the article.

REFERENCES

Arnone, E., Dialynas, Y. G., Noto, L. V., & Bras, R. L. (2016). Accounting for soil parameter uncertainty in a physically based and distributed approach for rainfall-triggered landslides. Hydrological Processes, 30(6), 927–944.
10.1002/hyp.10609
Web of Science® Google Scholar
Basile, A., Mele, G., & Terribile, F. (2003). Soil hydraulic behaviour of a selected benchmark soil involved in the landslide of Sarno 1998. Geoderma, 117, 331–346.
10.1016/S0016-7061(03)00132-0
Web of Science® Google Scholar
Baum, R. L., Godt, J. W., & Savage, W. Z. (2010). Estimating the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration. Journal of Geophysical Research, 115, F03013.
10.1029/2009JF001321
Web of Science® Google Scholar
Bertoldi, G., Della Chiesa, S., Notarnicola, C., Pasolli, L., Niedrist, G., & Tappeiner, U. (2014). Estimation of soil moisture patterns in mountain grasslands by means of SAR RADARSAT2 images and hydrological modeling. Journal of Hydrology, 516, 245–257.
10.1016/j.jhydrol.2014.02.018
Web of Science® Google Scholar
Bertoldi, G., Notarnicola, C., Leitinger, G., Endrizzi, S., Zebisch, M., Della Chiesa, S., & Tappeiner, U. (2010). Topographical and ecohydrological controls on land surface temperature in an alpine catchment. Ecohydrology, 3, 189–204.
10.1002/eco.129
Web of Science® Google Scholar
Bertoldi, G., Rigon, R., & Over, T. M. (2006). Impact of watershed geomorphic characteristics on the energy and water budgets. Journal of Hydrometeorology, 7(3), 389–403.
10.1175/JHM500.1
Web of Science® Google Scholar
Best, M. J. (1998). A model to predict surface temperatures. Boundary-Layer Meteorology, 88(2), 279–306.
10.1023/A:1001151927113
Web of Science® Google Scholar
Bilotta, E., Cascini, L., Foresta, V., & Sorbino, G. (2005). Geotechnical characterisation of pyroclastic soils involved in huge flowslides. Geotechnical and Geological Engineering, 23, 365–402.
10.1007/s10706-004-1607-3
Google Scholar
Brutsaert, W. (1975a). On a derivable formula for long-wave radiation from clear skies. Water Resources Research, 11, 742–744.
10.1029/WR011i005p00742
Web of Science® Google Scholar
Brutsaert, W. (1975b). A theory for local evaporation (or heat transfer) from rough and smooth surfaces at ground level. Water Resources Research, 11, 543–550.
10.1029/WR011i004p00543
Web of Science® Google Scholar
Capparelli, G., Damiano, E., Greco, R., Olivares, L., & Spolverino, G. (2020). Physical modelling investigation of rainfall infiltration in steep layered volcanoclastic slope. Journal of Hydrology, 580, 124199.
10.1016/j.jhydrol.2019.124199
Google Scholar
Capparelli, G., & Spolverino, G. (2020). An empirical approach for modeling hysteresis behavior of pyroclastic soils. Hydrology, 7, 14.
10.3390/hydrology7010014
Web of Science® Google Scholar
Capparelli, G., & Spolverino, G. (2022). Hydrological monitoring of a slope covered by stratified pyroclastic deposits and analysis of infiltration processes. Hydrological Processes, 36(6), e14634.
10.1002/hyp.14634
Web of Science® Google Scholar
Capparelli, G., & Versace, P. (2014). Analysis of landslide triggering conditions in the Sarno area using a physically based model. Hydrology and Earth System Sciences, 18, 3225–3237.
10.5194/hess-18-3225-2014
Web of Science® Google Scholar
Cascini, L. (2004). The flowslide of May 1998 in the Campania region, Italy: Scientific emergency management. Rivista italiana di geotecnica, 2, 11–44.
Google Scholar
Cascini, L., Cuomo, S., & Guida, D. (2008). Typical source areas of May 1998 flow-like mass movements in the Campania region, Southern Italy. Engineering Geology, 96, 107–125.
10.1016/j.enggeo.2007.10.003
Web of Science® Google Scholar
Cascini, L., Sorbino, G., Cuomo, S., & Ferlisi, S. (2014). Seasonal effects of rainfall on the shallow pyroclastic deposits of the Campania region (southern Italy). Landslides, 11, 779–792.
10.1007/s10346-013-0395-3
Web of Science® Google Scholar
Comegna, L., Damiano, E., Greco, R., Guida, A., Olivares, L., & Picarelli, L. (2016). Field hydrological monitoring of a sloping shallow pyroclastic deposit. Canadian Geotechnical Journal, 53, 1125–1137.
10.1139/cgj-2015-0344
Web of Science® Google Scholar
Costanzo, S., Di Massa, G., Costanzo, A., Morrone, L., Raffo, A., Spadafora, A., Borgia, A., Formetta, G., Capparelli, G., & Versace, P. (2015). Low-cost radars integrated into a landslide early warning system. Advances in Intelligent Systems and Computing, 354, 11–19.
10.1007/978-3-319-16528-8_2
Google Scholar
Crosta, G. B., & Dal Negro, P. (2003). Observations and modelling of soil slip-debris flow initiation processes in pyroclastic deposits: The Sarno 1998 event. Natural Hazards and Earth System Sciences, 3, 53–69.
10.5194/nhess-3-53-2003
Web of Science® Google Scholar
Dai, F. C., & Lee, C. F. (2002). Landslide characteristics and slope instability modeling using GIS, Lantau Island, Hong Kong. Geomorphology, 42(3–4), 213–228.
10.1016/S0169-555X(01)00087-3
Web of Science® Google Scholar
Damiano, E. (2019). Effects of layering on triggering mechanisms of rainfall-induced landslides in unsaturated pyroclastic granular soils. Canadian Geotechnical Journal, 56, 1278–1290.
10.1139/cgj-2018-0040
Web of Science® Google Scholar
Damiano, E., Greco, R., Guida, A., Olivares, L., & Picarelli, L. (2017). Investigation on rainwater infiltration into layered shallow covers in pyroclastic soils and its effect on slope stability. Engineering Geology, 220, 208–218.
10.1016/j.enggeo.2017.02.006
Web of Science® Google Scholar
Damiano, E., & Olivares, L. (2010). The role of infiltration processes in steep slope stability of pyroclastic granular soils: Laboratory and numerical investigation. Natural Hazards, 52, 329–350.
10.1007/s11069-009-9374-3
Web of Science® Google Scholar
Damiano, E., Olivares, L., & Picarelli, L. (2012). Steep-slope monitoring in unsaturated pyroclastic soils. Engineering Geology, 137–138, 1–12.
10.1016/j.enggeo.2012.03.002
Google Scholar
De Vita, P., Fusco, F., Tufano, R., & Cusano, D. (2018). Seasonal and event-based hydrological and slope stability modeling of pyroclastic fall deposits covering slopes in Campania (southern Italy). Water, 10, 1140.
10.3390/w10091140
Web of Science® Google Scholar
De Vita, P., Napolitano, N., Godt, J., & Baum, R. (2013). Deterministic estimation of hydrological thresholds for shallow landslide initiation and slope stability models: Case study from the Somma-Vesuvius area of southern Italy. Landslides, 10, 713–728.
10.1007/s10346-012-0348-2
Web of Science® Google Scholar
Deardorff, J. W. (1978). Efficient prediction of ground surface temperature and moisture, with inclusion of a layer of vegetation. Journal of Geophysical Research, 83(C4), 1889–1903.
10.1029/JC083iC04p01889
Web of Science® Google Scholar
Emberson, R., Kirschbaum, D., & Stanley, T. (2020). New global characterisation of landslide exposure. Natural Hazards and Earth System Sciences, 20, 3413–3424.
10.5194/nhess-20-3413-2020
Web of Science® Google Scholar
Endrizzi, S., Gruber, S., Dall'Amico, M., & Rigon, R. (2014). GEOtop 2.0: Simulating the combined energy and water balance at and below the land surface accounting for soil freezing, snow cover and terrain effects. Geoscientific Model Development, 7, 2831–2857.
10.5194/gmd-7-2831-2014
Web of Science® Google Scholar
Endrizzi, S., Matteo Dall’Amico, M., Stephan Gruber, S., & Riccardo Rigon, R. (2017). GEOtop Users Manual. https://geotopmodel.github.io/geotop/materials/geotop_manuale.pdf
Google Scholar
Endrizzi, S., & Marsh, P. (2010). Observations and modeling of turbulent fluxes during melt at the shrub-tundra transition zone 1: Point scale variations. Hydrology Research, 41, 471–491.
10.2166/nh.2010.149
Web of Science® Google Scholar
Feddes, R. A., Hoff, H., Bruen, M., Dawson, T., de Rosnay, P., Dirmeyer, P., & Pitman, A. J. (2001). Modeling root water uptake in hydrological and climate models. Bulletin of the American Meteorological Society, 82(12), 2797–2809.
10.1175/1520-0477(2001)082<2797:MRWUIH>2.3.CO;2
Web of Science® Google Scholar
Fiddes, J., Endrizzi, S., & Gruber, S. (2015). Large-area land surface simulations in heterogeneous terrain driven by global datasets: Application to mountain permafrost. The Cryosphere, 9, 411–426.
10.5194/tc-9-411-2015
Web of Science® Google Scholar
Formetta, G., & Capparelli, G. (2019). Quantifying the three-dimensional effects of anisotropic soil horizons on hillslope hydrology and stability. Journal of Hydrology, 570, 329–342.
10.1016/j.jhydrol.2018.12.064
Web of Science® Google Scholar
Formetta, G., Capparelli, G., & Versace, P. (2016). Evaluating performance of simplified physically based models for shallow landslide susceptibility. Hydrology and Earth System Sciences, 20, 4585–4603.
10.5194/hess-20-4585-2016
Web of Science® Google Scholar
Formetta, G., Simoni, S., Godt, J. W., Lu, N., & Rigon, R. (2016). Geomorphological control on variably saturated hillslope hydrology and slope instability. Water Resources Research, 52, 4590–4607.
10.1002/2015WR017626
Web of Science® Google Scholar
Fusco, F., Alloca, V., & De Vita, P. (2017). Hydro-geomorphological modelling of ash-fall pyroclastic soils for debris flow initiation and groundwater recharge in Campania (southern Italy). Catena, 158, 235–249.
10.1016/j.catena.2017.07.010
Web of Science® Google Scholar
Garratt, J. R. (1992). The atmospheric boundary layer (p. 316). Cambridge University Press.
Google Scholar
Greco, R., Comegna, L., Damiano, E., Guida, A., Olivares, L., & Picarelli, L. (2013). Hydrological modelling of a slope covered with shallow pyroclastic deposits from field monitoring data. Hydrology and Earth System Sciences, 17, 4001–4013.
10.5194/hess-17-4001-2013
Web of Science® Google Scholar
Greco, R., Marino, P., & Bogaard, T. A. (2023). Recent advancements of landslide hydrology. Wiley Interdisciplinary Reviews Water, 10(6), e1675.
10.1002/wat2.1675
Google Scholar
Gubler, S., Endrizzi, S., Gruber, S., & Purves, R. S. (2013). Sensitivities and uncertainties of modeled ground temperatures in mountain environments. Geoscientific Model Development, 6(4), 1319–1336.
10.5194/gmd-6-1319-2013
Web of Science® Google Scholar
Gupta, H. V., Kling, H., Yilmaz, K. K., & Martinez, G. F. (2009). Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. Journal of Hydrology, 377(1–2), 80–91.
10.1016/j.jhydrol.2009.08.003
Web of Science® Google Scholar
Hübner, R., Günther, T., Heller, K., Noell, U., & Kleber, A. (2017). Impacts of a capillary barrier on infiltration and subsurface stormflow in layered slope deposits monitored with 3-D ERT and hydrometric measurements. Hydrology and Earth System Sciences, 21(10), 5181–5199.
10.5194/hess-21-5181-2017
CAS Web of Science® Google Scholar
Hungr, O., Evans, S., & G., Bovis, M. (2001). Review of the classification of landslides of the flow type. Environmental and Engineering Geoscience, 7, 221–238.
10.2113/gseegeosci.7.3.221
Web of Science® Google Scholar
Iqbal, M. (1983). An introduction to solar radiation. Academic Press, 390, 1–390.
Google Scholar
Lu, N., Kaya, B. S., & Godt, J. W. (2011). Direction of unsaturated flow in a homogeneous and isotropic hillslope. Water Resources Research, 47, W02519.
10.1029/2010WR010003
Google Scholar
Mancarella, D., Doglioni, A., & Simeone, V. (2012). On capillary barrier effects and debris slide triggering in unsaturated layered covers. Engineering Geology, 147–148, 14–27.
10.1016/j.enggeo.2012.07.003
Web of Science® Google Scholar
Mancarella, D., & Simeone, V. (2012). Capillary barrier effects in unsaturated layered soils, with special reference to the pyroclastic veneer of the Pizzo d'Alvano, Campania, Italy. Bulletin of Engineering Geology and the Environment, 71, 791–801.
10.1007/s10064-012-0419-6
Google Scholar
Mualem, Y. (1976). A new model predicting the hydraulic conductivity of unsaturated porous media. Water Resources Research, 12, 513–522.
10.1029/WR012i003p00513
PubMed Web of Science® Google Scholar
Napolitano, E., Fusco, F., Baum, R. L., Godt, J. W., & De Vita, P. (2016). Effect of antecedent-hydrological conditions on rainfall triggering of debris flows in ash-fall pyroclastic mantled slopes of Campania (southern Italy). Landslides, 13, 967–983.
10.1007/s10346-015-0647-5
Web of Science® Google Scholar
Olivares, L., & Damiano, E. (2007). Postfailure mechanics of landslides: Laboratory investigation of flowslides in Py-roclastic soils. Journal of Geotechnical and Geoenviromental Engineering, 133, 51–62.
10.1061/(ASCE)1090-0241(2007)133:1(51)
Web of Science® Google Scholar
Olivares, L., & Picarelli, L. (2003). Shallow flowslides triggered by intense rainfalls on natural slopes covered by loose unsaturated pyroclastic soils. Geotechnique, 53(2), 283–287.
10.1680/geot.2003.53.2.283
Google Scholar
Picarelli, L., Damiano, E., Greco, R., Minardo, A., Olivares, L., & Zeni, L. (2015). Performance of slope behavior indicators in unsaturated pyroclastic soils. Journal of Mountain Science, 12(6), 1434–1447.
10.1007/s11629-014-3104-3
Web of Science® Google Scholar
Picarelli, L., Evangelista, A., Rolandi, G., Paone, A., Nicotera, M. V., Olivares, L., & Rolandi, M. (2006). Mechanical properties of pyroclastic soils in campania region. In proceedings of the 2nd international workshop on characterisation and engineering properties of natural soils, Singapore.
Google Scholar
Rigon, R., Bertoldi, G., & Over, T. M. (2006). GEOtop: A distributed hydrological model with coupled water and energy budgets. Journal of Hydrometeorology, 7(3), 371–388.
10.1175/JHM497.1
Web of Science® Google Scholar
Roman Quintero, D. C., Damiano, E., Olivares, L., & Greco, R. (2024). Mechanical and hydraulic properties of unsaturated layered pyroclastic ashes in landslide-prone areas of Campania (Italy). Bulletin of Engineering Geology and the Environment, 83(7), 291.
10.1007/s10064-024-03783-x
Google Scholar
Smith, R. E., & Hebbert, R. H. B. (1979). A Monte Carlo analysis of the hydrologic effects of spatial variability of infiltration. Water Resources Research, 15, 419–429.
10.1029/WR015i002p00419
Web of Science® Google Scholar
Sorbino, G., & Foresta, V. (2002). Unsaturated hydraulic characteristics of pyroclastic soils. Proceeding of the 3rd international conference on unsaturated soils, Recife, Balkema, Rotter-dam. 1, 405–410.
Google Scholar
Sorbino, G., Sica, C., & Cascini, L. (2010). Susceptibility analysis of shallow landslides source areas using physically based models. Natural Hazards, 53, 313–332.
10.1007/s11069-009-9431-y
Google Scholar
Sousa, L., Vargas, E., Jr., Sousa, R., & Chaminè, H. I. (2020). Hydrological risks in natural hazards focused on the role of the water: Studies on land-slides. In Advances in natural hazards and hydrological risks: Meeting the challenge. Advances in science, technology innovation (pp. 43–47). Springer.
Google Scholar
Spolverino, G., Capparelli, G., & Versace, P. (2019). An instrumented flume for infiltration process modeling, Landslide Triggering and Propagation. Geosciences, 9, 108.
10.3390/geosciences9030108
CAS Google Scholar
Stormont, J. C., & Anderson, C. E. (1999). Capillary barrier effect from underlying coarser soil layer. Journal of Geotechnical and Geoenvironmental Engineering, 125(8), 641–648.
10.1061/(ASCE)1090-0241(1999)125:8(641)
Web of Science® Google Scholar
Tufano, R., Formetta, G., Calcaterra, D., & De Vita, P. (2021). Hydrological control of soil thickness spatial variability on the initiation of rainfall-induced shallow landslides using a three-dimensional model. Landslides, 18, 3367–3380.
10.1007/s10346-021-01681-x
Web of Science® Google Scholar
Van Genuchten, M. T. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal, 44, 892–898.
10.2136/sssaj1980.03615995004400050002x
Web of Science® Google Scholar
Warrick, A. W., Wierenga, P. J., & Pan, L. (1997). Downward water flow through sloping layers in the vadose zone: Analytical solutions for diversions. Journal of Hydrology, 192(1–4), 321–337.
10.1016/S0022-1694(96)03080-6
Web of Science® Google Scholar
Wigmosta, M. S., Vail, L. W., & Lettenmaier, D. P. (1994). A distributed hydrology—Vegetation model for complex terrain. Water Resources Research, 30(6), 1665–1679.
10.1029/94WR00436
Web of Science® Google Scholar

Volume38, Issue8

August 2024

e15257

Exploring hydrological dynamics of layered pyroclastic soils by combining laboratory and field experiments with a numerical model

Abstract

1 INTRODUCTION

2 STUDY AREA AND SOIL PROPERTIES